苏科版七年级数学下册 7.4 认识三角形 复习课件(共15张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.4 认识三角形 复习课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 579.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 09:35:57 | ||
图片预览


文档简介
(共15张PPT)
7.4 认识三角形
知识点回顾
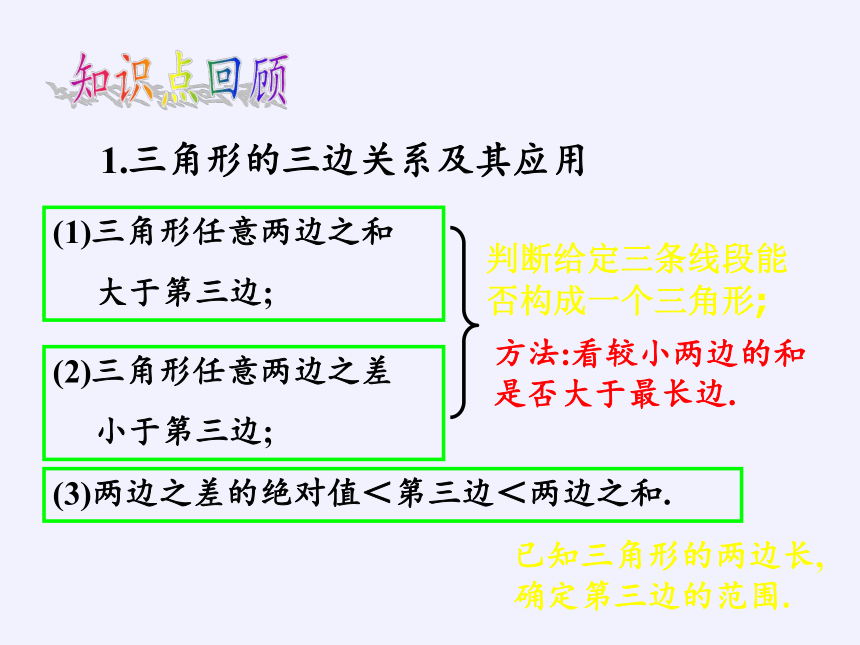
1.三角形的三边关系及其应用
(1)三角形任意两边之和
大于第三边;
(2)三角形任意两边之差
小于第三边;
(3)两边之差的绝对值<第三边<两边之和.
判断给定三条线段能否构成一个三角形;
已知三角形的两边长,确定第三边的范围.
方法:看较小两边的和是否大于最长边.
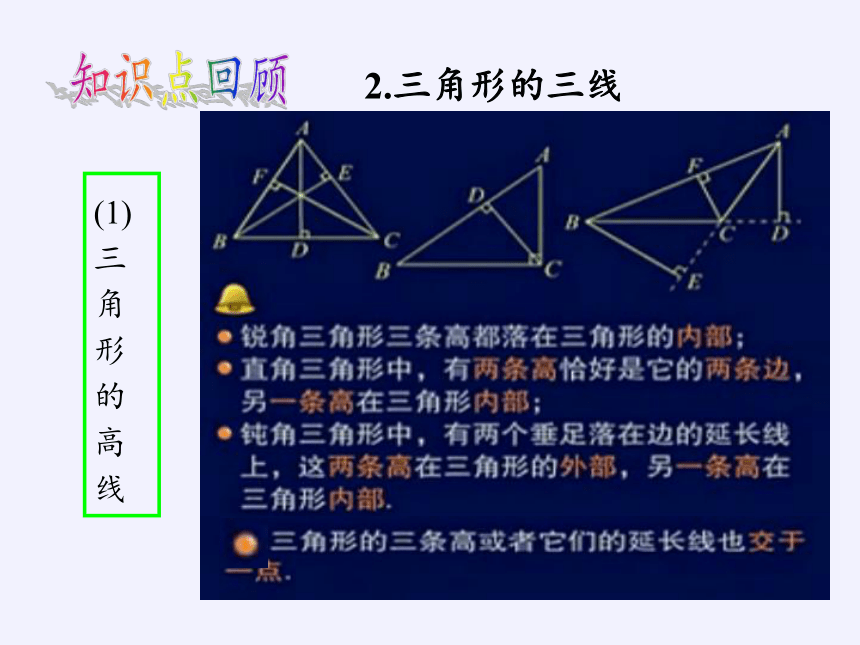
2.三角形的三线
知识点回顾
(1)
三
角
形
的
高
线
2.三角形的三线
知识点回顾
(1)
三
角
形
的
高
线
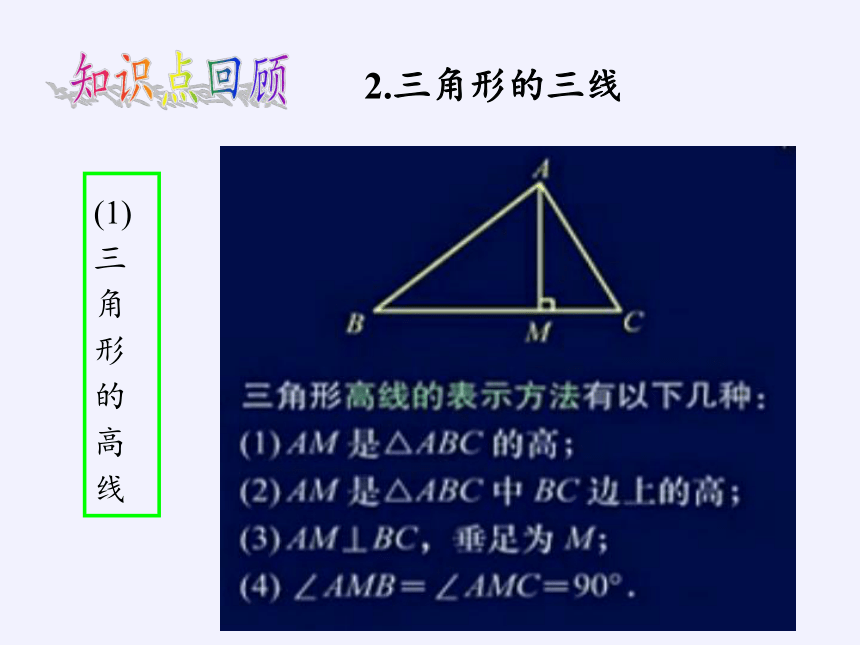
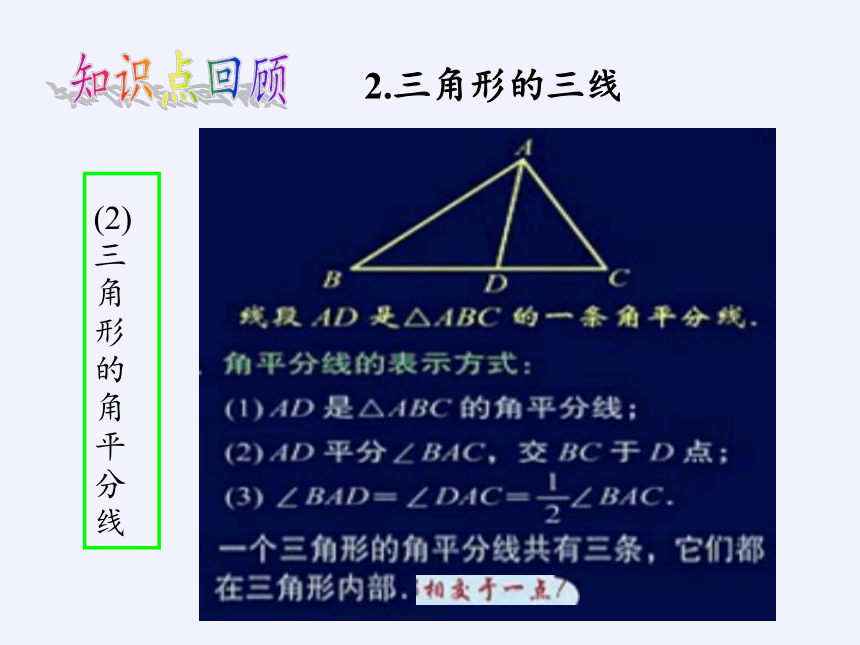
2.三角形的三线
知识点回顾
(2)
三
角
形
的
角
平
分
线
2.三角形的三线
知识点回顾
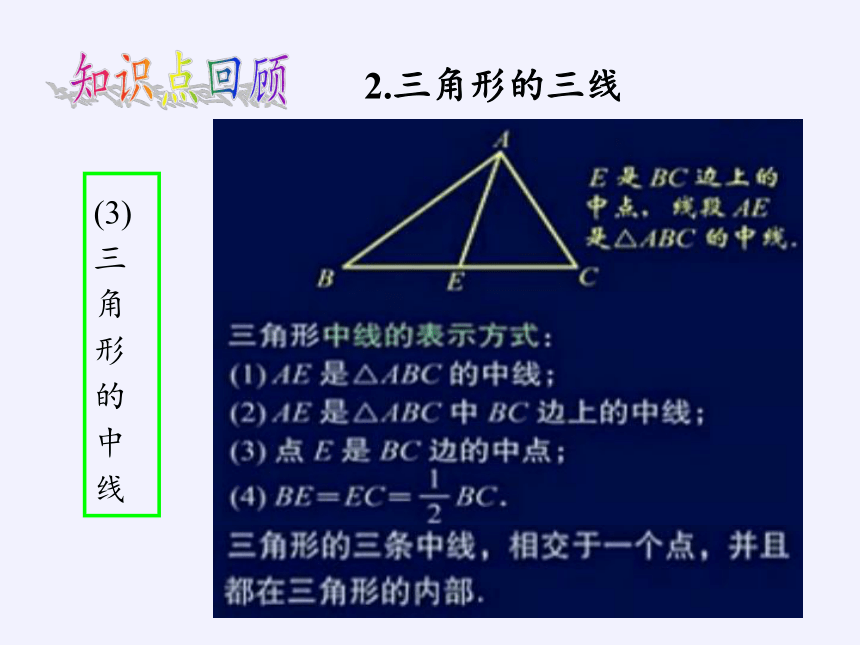
(3)
三
角
形
的
中
线
例1
例题学习
如图,AD是△ABC的角平分线,DE∥CA,并且交AB于点E, DF∥BA,交AC于点F,∠1与∠2是否相等
3
4
例2
例题学习
你能把一个三角形分成面积相等的2个三角形吗 能分成面积相等的4个三角形吗 试试看.
例3
例题学习
如图,AD、CE是△ABC的高,AB=2BC,AD与CE有怎样的数量关系?为什么?
等积法思想:
一个图形从两个不同
角度计算所得的面积
相等。
例4
例题学习
如图,在△ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成周长差为2cm的两个三角形。
求△ABC各边的长。
分类讨论思想
课堂小结
1.会正确利用三角形的“三线”条件来解题;
2.等积法思想的运用;
3.分类讨论法思想的运用;
课堂练习
补充习题7页—8页
能力拓展
1
如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD。
试说明:AD是△ABC的角平分线。
能力拓展
2
如图,S△ABC=1, S△BDE= S△DEC= S△ACE。
求△ADE的面积。
谢 谢
7.4 认识三角形
知识点回顾
1.三角形的三边关系及其应用
(1)三角形任意两边之和
大于第三边;
(2)三角形任意两边之差
小于第三边;
(3)两边之差的绝对值<第三边<两边之和.
判断给定三条线段能否构成一个三角形;
已知三角形的两边长,确定第三边的范围.
方法:看较小两边的和是否大于最长边.
2.三角形的三线
知识点回顾
(1)
三
角
形
的
高
线
2.三角形的三线
知识点回顾
(1)
三
角
形
的
高
线
2.三角形的三线
知识点回顾
(2)
三
角
形
的
角
平
分
线
2.三角形的三线
知识点回顾
(3)
三
角
形
的
中
线
例1
例题学习
如图,AD是△ABC的角平分线,DE∥CA,并且交AB于点E, DF∥BA,交AC于点F,∠1与∠2是否相等
3
4
例2
例题学习
你能把一个三角形分成面积相等的2个三角形吗 能分成面积相等的4个三角形吗 试试看.
例3
例题学习
如图,AD、CE是△ABC的高,AB=2BC,AD与CE有怎样的数量关系?为什么?
等积法思想:
一个图形从两个不同
角度计算所得的面积
相等。
例4
例题学习
如图,在△ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成周长差为2cm的两个三角形。
求△ABC各边的长。
分类讨论思想
课堂小结
1.会正确利用三角形的“三线”条件来解题;
2.等积法思想的运用;
3.分类讨论法思想的运用;
课堂练习
补充习题7页—8页
能力拓展
1
如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD。
试说明:AD是△ABC的角平分线。
能力拓展
2
如图,S△ABC=1, S△BDE= S△DEC= S△ACE。
求△ADE的面积。
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
