2021-2022学年湘教版七年级下册数学第4章相交线与平行线单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版七年级下册数学第4章相交线与平行线单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 18:08:21 | ||
图片预览



文档简介
2021-2022学年湘教新版七年级下册数学《第4章 相交线与平行线》单元测试卷
一.选择题(共10小题,满分30分)
1.下列说法正确的个数是( )
①连接两点的线中以线段最短;
②两条直线相交,有且只有一个交点;
③若两条直线有两个公共点,则这两条直线重合;
④若AB+BC=AC,则A、B、C三点共线.
A.1 B.2 C.3 D.4
2.公园里准备修五条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设( )
A.9个 B.10个 C.11个 D.12个
3.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.同一平面内有三条直线,如果只有两条平行,那么它们交点的个数为( )
A.0 B.1 C.2 D.3
5.经过直线外一点,有几条直线和已知直线平行( )
A.0条 B.1条 C.2条 D.3条
6.下列A、B、C、D四幅图案中,能通过平移如图图案得到的是( )
A. B. C. D.
7.如图,Rt△ABC沿直线边BC所在的直线向右平移得到△DEF,下列结论中不一定正确的是( )
A.∠DEF=90°
B.BE=CF
C.CE=CF
D.S四边形ABEH=S四边形DHCF
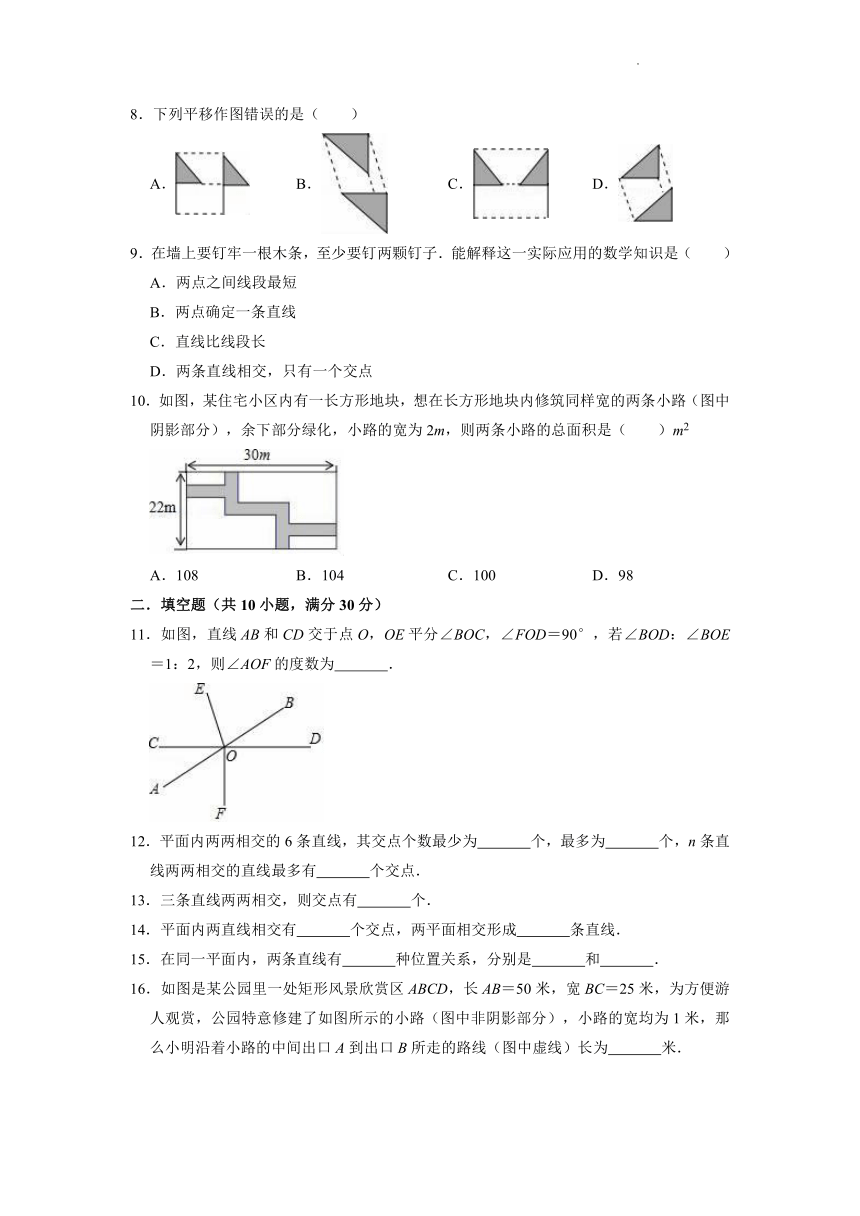
8.下列平移作图错误的是( )
A. B. C. D.
9.在墙上要钉牢一根木条,至少要钉两颗钉子.能解释这一实际应用的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.直线比线段长
D.两条直线相交,只有一个交点
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108 B.104 C.100 D.98
二.填空题(共10小题,满分30分)
11.如图,直线AB和CD交于点O,OE平分∠BOC,∠FOD=90°,若∠BOD:∠BOE=1:2,则∠AOF的度数为 .
12.平面内两两相交的6条直线,其交点个数最少为 个,最多为 个,n条直线两两相交的直线最多有 个交点.
13.三条直线两两相交,则交点有 个.
14.平面内两直线相交有 个交点,两平面相交形成 条直线.
15.在同一平面内,两条直线有 种位置关系,分别是 和 .
16.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为 米.
17.用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形,要将它按图的方式向外等距扩1(单位:cm),得到新的正方形,则这根铁丝需增加 cm.
18.如图:PC∥AB,QC∥AB,则点P、C、Q在一条直线上.
理由是: .
19.如图,将Rt△ABC沿BC方向平移得到Rt△DEF,如果AB=12cm,BE=5cm,DH=4cm,则图中阴影部分面积为 cm2.
20.在平面直角坐标系xOy中,对点P进行如下操作:把点P的横、纵坐标乘以同一个实数a,将得到的点先向左平移m个单位长度,再向上平移n个单位长度,得到点P的对应点P′.如图,点A,B经过上述操作后得到的对应点分别是点A′,B′.
(1)如果点C(6,﹣2)经过上述操作后得到的对应点是点C′,那么点C′的坐标为 .
(2)如果点D经过上述操作后得到的对应点D′与点D重合,那么点D的坐标为 .
三.解答题(共7小题,满分60分)
21.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
22.(1)直线l1与l2是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第三条直线l3,则这三条直线最多有 个交点;
(2)如果在(1)的基础上在这个平面内再画第四条直线l4,则这四条直线最多可有 个交点.
(3)由(1)(2)我们可以猜想:在同一平面内,n(n>1)条直线最多有 个交点.
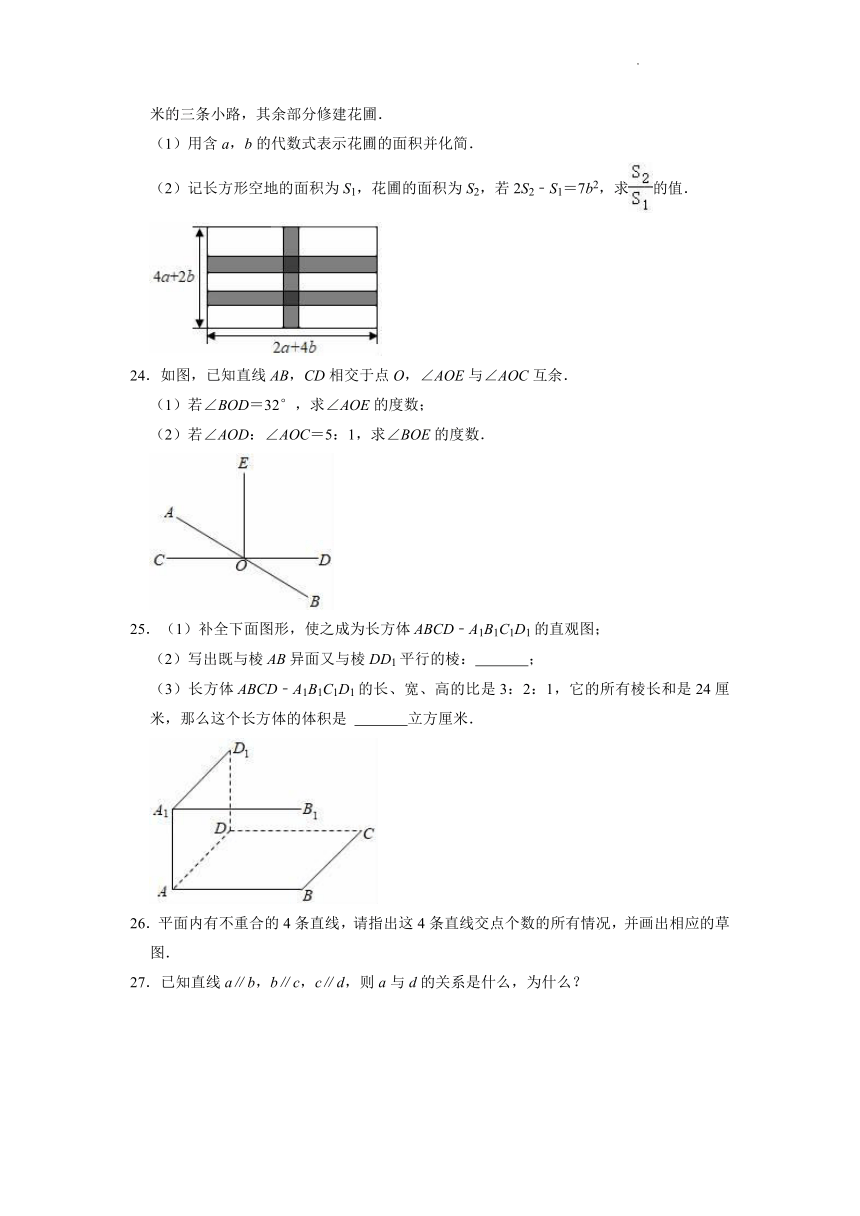
23.某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.
(1)用含a,b的代数式表示花圃的面积并化简.
(2)记长方形空地的面积为S1,花圃的面积为S2,若2S2﹣S1=7b2,求的值.
24.如图,已知直线AB,CD相交于点O,∠AOE与∠AOC互余.
(1)若∠BOD=32°,求∠AOE的度数;
(2)若∠AOD:∠AOC=5:1,求∠BOE的度数.
25.(1)补全下面图形,使之成为长方体ABCD﹣A1B1C1D1的直观图;
(2)写出既与棱AB异面又与棱DD1平行的棱: ;
(3)长方体ABCD﹣A1B1C1D1的长、宽、高的比是3:2:1,它的所有棱长和是24厘米,那么这个长方体的体积是 立方厘米.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
27.已知直线a∥b,b∥c,c∥d,则a与d的关系是什么,为什么?
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:①线段的基本性质是:所有连接两点的线中,线段最短.故本选项正确;
②任意两个点可以通过一条直线连接,所以,两条直线相交,有且只有一个交点,故本选项正确;
③任意两个点可以通过一条直线连接,若两条直线有两个公共点,则这两条直线重合;故本选项正确;
④由两点间的距离公式可知,点A、B、C共线,故本选项正确;
综上所述,以上说法正确的是①②③④共4个.
故选:D.
2.解:因为一平面内n条直线最多有交点,
所以,五条甬道可设的报亭数为=10.
故选:B.
3.解:A、∠1与∠2不是对顶角;
B、∠1与∠2不是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2是对顶角;
故选:D.
4.解:根据题意,第三条直线与这两条平行直线各有一个交点.
故选:C.
5.解:根据平行公理,即过直线外一点,有且只有一条直线和已知直线平行.
故选:B.
6.解:由平移的性质可知,不改变图形的形状、大小和方向,只有A选项符合要求,
故选:A.
7.解:∵Rt△ABC沿直线边BC所在的直线向右平移得到△DEF,
∴∠DEF=∠ABC=90°,BC=EF,S△ABC=S△DEF,
∴BC﹣EC=EF﹣EC,S△ABC﹣S△HEC=S△DEF﹣S△HEC,
∴BE=CF,S四边形ABEH=S四边形DHCF,
但不能得出CE=CF,
故选:C.
8.解:A、B、D符合平移变换,C是轴对称变换.
故选:C.
9.解:在墙上固定一根木条,至少需要钉两颗钉子.能解释这一实际应用的数学知识是两点确定一条直线.
故选:B.
10.解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故选:C.
二.填空题(共10小题,满分30分)
11.解:∵∠BOD:∠BOE=1:2,OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=1:2:2,
∴∠BOD=36°,
∴∠AOC=36°,
又∵∠COF=∠DOF=90°,
∴∠AOF=90°﹣36°=54°.
故答案为:54°.
12.解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1==1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2==3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3==6);
若平面内有两两相交的5条直线,则最多有10个交点;(即:1+2+3+4==10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;(即1+2+3+4+5==15);
若平面内有n条直线两两相交,则最多有个交点;
故答案为:1,15,.
13.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
14.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
15.解:在同一平面内,两条直线有两种位置关系,分别是平行和相交.
故答案为:两;平行;相交.
16.解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD﹣1)×2,
∴图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为50+(25﹣1)×2=98米,
故答案为:98.
17.解:∵原正方形的周长为acm,
∴原正方形的边长为cm,
∵将它按如图的方式向外等距扩1cm,
∴新正方形的边长为(+2)cm,
则新正方形的周长为(a+8)cm,
因此需要增加的长度为a+8﹣a=8cm.
故答案为:8.
18.解:∵PC∥AB,QC∥AB,
∵PC和CQ都过点C,
∴P、C、Q在一条直线上(过直线外一点有且只有一条直线与已知直线平行),
故答案为:过直线外一点有且只有一条直线与已知直线平行.
19.解:∵Rt△ABC沿BC方向平移得到Rt△DEF,
∴AB=DE=12cm,△ABC≌△DEF,
∴阴影部分面积=梯形ABEH的面积,
∵DH=4cm,
∴EH=12﹣4=8cm,
∴阴影部分面积=×(8+12)×5=50cm2.
故答案为:50.
20.解:(1)∵点A的横坐标为0,0×a=0,
又∵平移的横坐标为﹣2,
∴m=2,
∵﹣5+2=﹣3,﹣6÷(﹣3)=2,
∴a=,
∵﹣2×=﹣1,﹣1+1=0,
∴n=1,
∴C(6,﹣2)→(3,﹣1)→(1,0),
故C′(1,0).
(2)设D(a,b),由题意, a﹣2=a, b+1=b,
解得a=﹣4,b=2,
∴D(﹣4,2).
故答案为:(﹣4,2).
三.解答题(共7小题,满分60分)
21.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
22.解:(1)三条直线相交交点最多为:1+2=3;
(2)四条直线相交交点最多为:1+2+3=6;
(3)五条直线相交交点最多为:1+2+3+4=10;
六条直线相交交点最多为:1+2+3+4+5=15;
…;
n条直线相交交点最多为:1+2+3+…+n﹣1=.
故答案为:3,6,.
23.解:(1)平移后图形为:(空白处为花圃的面积)
所以花圃的面积=(4a+2b﹣2a)(2a+4b﹣a)
=(2a+2b)(a+4b)
=2a2+8ab+2ab+8b2
=2a2+10ab+8b2;
(2)S1=(4a+2b)(2a+4b)=8a2+20ab+8b2,
S2=2a2+10ab+8b2;
∵2S2﹣S1=7b2,
∴2(2a2+10ab+8b2)﹣(8a2+20ab+8b2)=7b2,
∴b2=4a2,
∴b=2a,
∴S1=8a2+40a2+32a2=80a2,S2=2a2+20a2+32a2=54a2,
∴==.
24.解:(1)因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=32°,
因为∠AOE与∠AOC互余,
所以∠AOE+∠AOC=90°,
所以∠AOE=90°﹣∠AOC
=90°﹣32°
=58°;
(2)因为∠AOD:∠AOC=5:1,
所以∠AOD=5∠AOC,
因为∠AOC+∠AOD=180°,
所以6∠AOC=180°,
则∠AOC=30°,
由(1)知∠BOD=∠AOC=30°,
因为∠COE=∠DOE=90°,
所以∠BOE=∠DOE+∠BOD
=90°+30°
=120°.
25.解:(1)画出图形如图:
(2)既与棱AB异面又与棱DD1平行的棱是CC1;
(3)24÷4=6(厘米),
6×=3(厘米);
6×=2(厘米);
6×=1(厘米).
3×2×1=6(立方厘米).
所以长方体的体积是6立方厘米.
故答案为:CC1,6.
26.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(6)当四条直线同交于一点时,只有1个交点,
(7)当四条直线两两相交,且不过同一点时,有6个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
27.解:a与d平行,理由如下:
因为a∥b,b∥c,
所以a∥c,
因为c∥d,
所以a∥d,
即平行具有传递性.
一.选择题(共10小题,满分30分)
1.下列说法正确的个数是( )
①连接两点的线中以线段最短;
②两条直线相交,有且只有一个交点;
③若两条直线有两个公共点,则这两条直线重合;
④若AB+BC=AC,则A、B、C三点共线.
A.1 B.2 C.3 D.4
2.公园里准备修五条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设( )
A.9个 B.10个 C.11个 D.12个
3.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.同一平面内有三条直线,如果只有两条平行,那么它们交点的个数为( )
A.0 B.1 C.2 D.3
5.经过直线外一点,有几条直线和已知直线平行( )
A.0条 B.1条 C.2条 D.3条
6.下列A、B、C、D四幅图案中,能通过平移如图图案得到的是( )
A. B. C. D.
7.如图,Rt△ABC沿直线边BC所在的直线向右平移得到△DEF,下列结论中不一定正确的是( )
A.∠DEF=90°
B.BE=CF
C.CE=CF
D.S四边形ABEH=S四边形DHCF
8.下列平移作图错误的是( )
A. B. C. D.
9.在墙上要钉牢一根木条,至少要钉两颗钉子.能解释这一实际应用的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.直线比线段长
D.两条直线相交,只有一个交点
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108 B.104 C.100 D.98
二.填空题(共10小题,满分30分)
11.如图,直线AB和CD交于点O,OE平分∠BOC,∠FOD=90°,若∠BOD:∠BOE=1:2,则∠AOF的度数为 .
12.平面内两两相交的6条直线,其交点个数最少为 个,最多为 个,n条直线两两相交的直线最多有 个交点.
13.三条直线两两相交,则交点有 个.
14.平面内两直线相交有 个交点,两平面相交形成 条直线.
15.在同一平面内,两条直线有 种位置关系,分别是 和 .
16.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为 米.
17.用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形,要将它按图的方式向外等距扩1(单位:cm),得到新的正方形,则这根铁丝需增加 cm.
18.如图:PC∥AB,QC∥AB,则点P、C、Q在一条直线上.
理由是: .
19.如图,将Rt△ABC沿BC方向平移得到Rt△DEF,如果AB=12cm,BE=5cm,DH=4cm,则图中阴影部分面积为 cm2.
20.在平面直角坐标系xOy中,对点P进行如下操作:把点P的横、纵坐标乘以同一个实数a,将得到的点先向左平移m个单位长度,再向上平移n个单位长度,得到点P的对应点P′.如图,点A,B经过上述操作后得到的对应点分别是点A′,B′.
(1)如果点C(6,﹣2)经过上述操作后得到的对应点是点C′,那么点C′的坐标为 .
(2)如果点D经过上述操作后得到的对应点D′与点D重合,那么点D的坐标为 .
三.解答题(共7小题,满分60分)
21.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
22.(1)直线l1与l2是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第三条直线l3,则这三条直线最多有 个交点;
(2)如果在(1)的基础上在这个平面内再画第四条直线l4,则这四条直线最多可有 个交点.
(3)由(1)(2)我们可以猜想:在同一平面内,n(n>1)条直线最多有 个交点.
23.某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.
(1)用含a,b的代数式表示花圃的面积并化简.
(2)记长方形空地的面积为S1,花圃的面积为S2,若2S2﹣S1=7b2,求的值.
24.如图,已知直线AB,CD相交于点O,∠AOE与∠AOC互余.
(1)若∠BOD=32°,求∠AOE的度数;
(2)若∠AOD:∠AOC=5:1,求∠BOE的度数.
25.(1)补全下面图形,使之成为长方体ABCD﹣A1B1C1D1的直观图;
(2)写出既与棱AB异面又与棱DD1平行的棱: ;
(3)长方体ABCD﹣A1B1C1D1的长、宽、高的比是3:2:1,它的所有棱长和是24厘米,那么这个长方体的体积是 立方厘米.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
27.已知直线a∥b,b∥c,c∥d,则a与d的关系是什么,为什么?
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:①线段的基本性质是:所有连接两点的线中,线段最短.故本选项正确;
②任意两个点可以通过一条直线连接,所以,两条直线相交,有且只有一个交点,故本选项正确;
③任意两个点可以通过一条直线连接,若两条直线有两个公共点,则这两条直线重合;故本选项正确;
④由两点间的距离公式可知,点A、B、C共线,故本选项正确;
综上所述,以上说法正确的是①②③④共4个.
故选:D.
2.解:因为一平面内n条直线最多有交点,
所以,五条甬道可设的报亭数为=10.
故选:B.
3.解:A、∠1与∠2不是对顶角;
B、∠1与∠2不是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2是对顶角;
故选:D.
4.解:根据题意,第三条直线与这两条平行直线各有一个交点.
故选:C.
5.解:根据平行公理,即过直线外一点,有且只有一条直线和已知直线平行.
故选:B.
6.解:由平移的性质可知,不改变图形的形状、大小和方向,只有A选项符合要求,
故选:A.
7.解:∵Rt△ABC沿直线边BC所在的直线向右平移得到△DEF,
∴∠DEF=∠ABC=90°,BC=EF,S△ABC=S△DEF,
∴BC﹣EC=EF﹣EC,S△ABC﹣S△HEC=S△DEF﹣S△HEC,
∴BE=CF,S四边形ABEH=S四边形DHCF,
但不能得出CE=CF,
故选:C.
8.解:A、B、D符合平移变换,C是轴对称变换.
故选:C.
9.解:在墙上固定一根木条,至少需要钉两颗钉子.能解释这一实际应用的数学知识是两点确定一条直线.
故选:B.
10.解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故选:C.
二.填空题(共10小题,满分30分)
11.解:∵∠BOD:∠BOE=1:2,OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=1:2:2,
∴∠BOD=36°,
∴∠AOC=36°,
又∵∠COF=∠DOF=90°,
∴∠AOF=90°﹣36°=54°.
故答案为:54°.
12.解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1==1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2==3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3==6);
若平面内有两两相交的5条直线,则最多有10个交点;(即:1+2+3+4==10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;(即1+2+3+4+5==15);
若平面内有n条直线两两相交,则最多有个交点;
故答案为:1,15,.
13.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
14.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
15.解:在同一平面内,两条直线有两种位置关系,分别是平行和相交.
故答案为:两;平行;相交.
16.解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD﹣1)×2,
∴图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为50+(25﹣1)×2=98米,
故答案为:98.
17.解:∵原正方形的周长为acm,
∴原正方形的边长为cm,
∵将它按如图的方式向外等距扩1cm,
∴新正方形的边长为(+2)cm,
则新正方形的周长为(a+8)cm,
因此需要增加的长度为a+8﹣a=8cm.
故答案为:8.
18.解:∵PC∥AB,QC∥AB,
∵PC和CQ都过点C,
∴P、C、Q在一条直线上(过直线外一点有且只有一条直线与已知直线平行),
故答案为:过直线外一点有且只有一条直线与已知直线平行.
19.解:∵Rt△ABC沿BC方向平移得到Rt△DEF,
∴AB=DE=12cm,△ABC≌△DEF,
∴阴影部分面积=梯形ABEH的面积,
∵DH=4cm,
∴EH=12﹣4=8cm,
∴阴影部分面积=×(8+12)×5=50cm2.
故答案为:50.
20.解:(1)∵点A的横坐标为0,0×a=0,
又∵平移的横坐标为﹣2,
∴m=2,
∵﹣5+2=﹣3,﹣6÷(﹣3)=2,
∴a=,
∵﹣2×=﹣1,﹣1+1=0,
∴n=1,
∴C(6,﹣2)→(3,﹣1)→(1,0),
故C′(1,0).
(2)设D(a,b),由题意, a﹣2=a, b+1=b,
解得a=﹣4,b=2,
∴D(﹣4,2).
故答案为:(﹣4,2).
三.解答题(共7小题,满分60分)
21.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
22.解:(1)三条直线相交交点最多为:1+2=3;
(2)四条直线相交交点最多为:1+2+3=6;
(3)五条直线相交交点最多为:1+2+3+4=10;
六条直线相交交点最多为:1+2+3+4+5=15;
…;
n条直线相交交点最多为:1+2+3+…+n﹣1=.
故答案为:3,6,.
23.解:(1)平移后图形为:(空白处为花圃的面积)
所以花圃的面积=(4a+2b﹣2a)(2a+4b﹣a)
=(2a+2b)(a+4b)
=2a2+8ab+2ab+8b2
=2a2+10ab+8b2;
(2)S1=(4a+2b)(2a+4b)=8a2+20ab+8b2,
S2=2a2+10ab+8b2;
∵2S2﹣S1=7b2,
∴2(2a2+10ab+8b2)﹣(8a2+20ab+8b2)=7b2,
∴b2=4a2,
∴b=2a,
∴S1=8a2+40a2+32a2=80a2,S2=2a2+20a2+32a2=54a2,
∴==.
24.解:(1)因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=32°,
因为∠AOE与∠AOC互余,
所以∠AOE+∠AOC=90°,
所以∠AOE=90°﹣∠AOC
=90°﹣32°
=58°;
(2)因为∠AOD:∠AOC=5:1,
所以∠AOD=5∠AOC,
因为∠AOC+∠AOD=180°,
所以6∠AOC=180°,
则∠AOC=30°,
由(1)知∠BOD=∠AOC=30°,
因为∠COE=∠DOE=90°,
所以∠BOE=∠DOE+∠BOD
=90°+30°
=120°.
25.解:(1)画出图形如图:
(2)既与棱AB异面又与棱DD1平行的棱是CC1;
(3)24÷4=6(厘米),
6×=3(厘米);
6×=2(厘米);
6×=1(厘米).
3×2×1=6(立方厘米).
所以长方体的体积是6立方厘米.
故答案为:CC1,6.
26.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(6)当四条直线同交于一点时,只有1个交点,
(7)当四条直线两两相交,且不过同一点时,有6个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
27.解:a与d平行,理由如下:
因为a∥b,b∥c,
所以a∥c,
因为c∥d,
所以a∥d,
即平行具有传递性.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
