2021-2022学年华东师大版九年级下册数学第27章圆单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级下册数学第27章圆单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 18:20:04 | ||
图片预览


文档简介
2021-2022学年华东师大新版九年级下册数学《第27章 圆》单元测试卷
一.选择题(共10小题,满分30分)
1.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.逐渐变大 B.逐渐变小 C.不变 D.不能确定
2.下列说法:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④长度相等的两条弧是等弧;⑤完全重合的两条弧是等弧.正确的命题有( )
A.1个 B.2个 C.3个 D.4个
3.如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,则截面上有油部分油面CD(单位:cm)等于( )
A.8cm B.9cm C.10cm D.11cm
4.如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30 B.45 C.50 D.60
5.如图,△ABC内接于⊙O,∠BAC=30°,BC=12,则⊙O的直径为( )
A.12 B.20 C.24 D.30
6.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
A.3 B. C.2.5 D.2
7.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
8.如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB等于( )
A.20° B.25° C.35° D.45°
9.东汉初年,我国的《周髀算经》里就有“径一周三”的古率,提出了圆的直径与周长之间存在一定的比例关系.将图中的半圆弧形铁丝()向右水平拉直(保持M端不动),根据该古率,与拉直后铁丝N端的位置最接近的是( )
A.点A B.点B C.点C D.点D
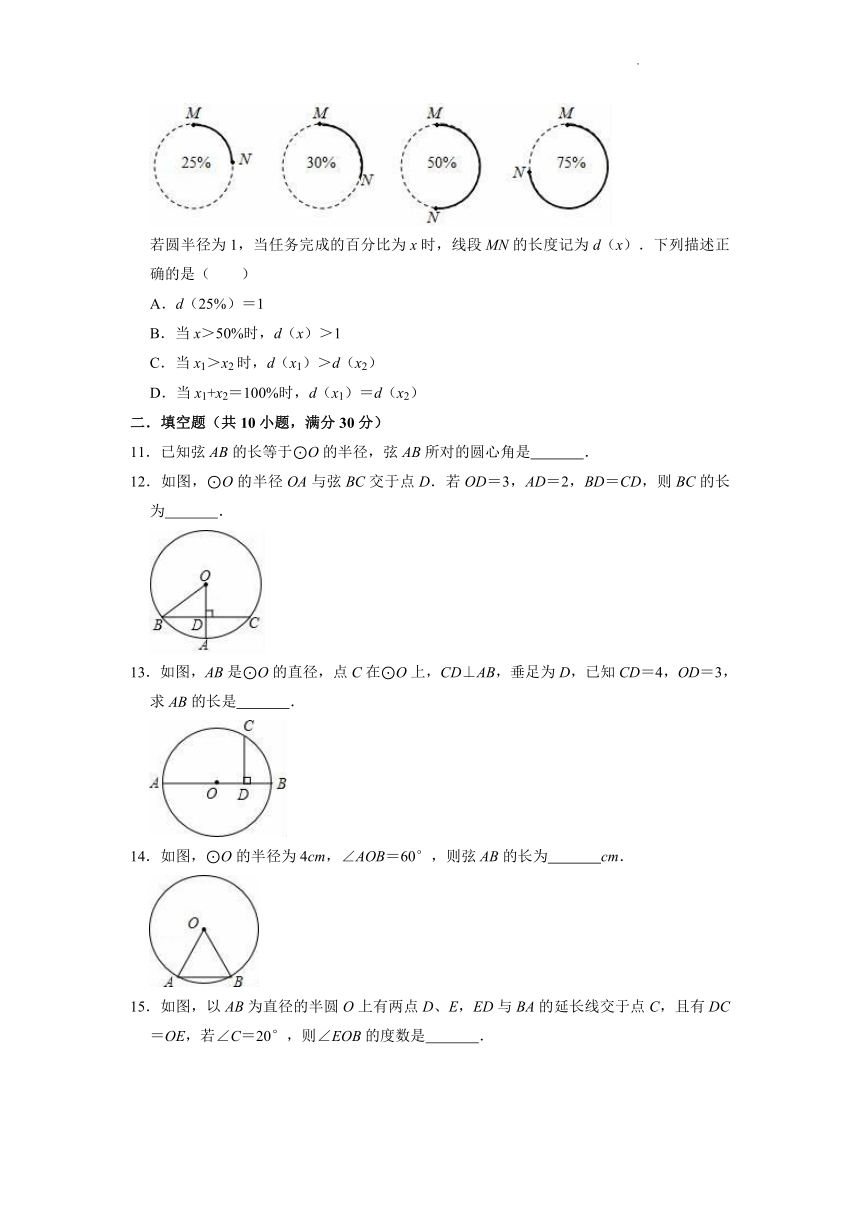
10.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
二.填空题(共10小题,满分30分)
11.已知弦AB的长等于⊙O的半径,弦AB所对的圆心角是 .
12.如图,⊙O的半径OA与弦BC交于点D.若OD=3,AD=2,BD=CD,则BC的长为 .
13.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
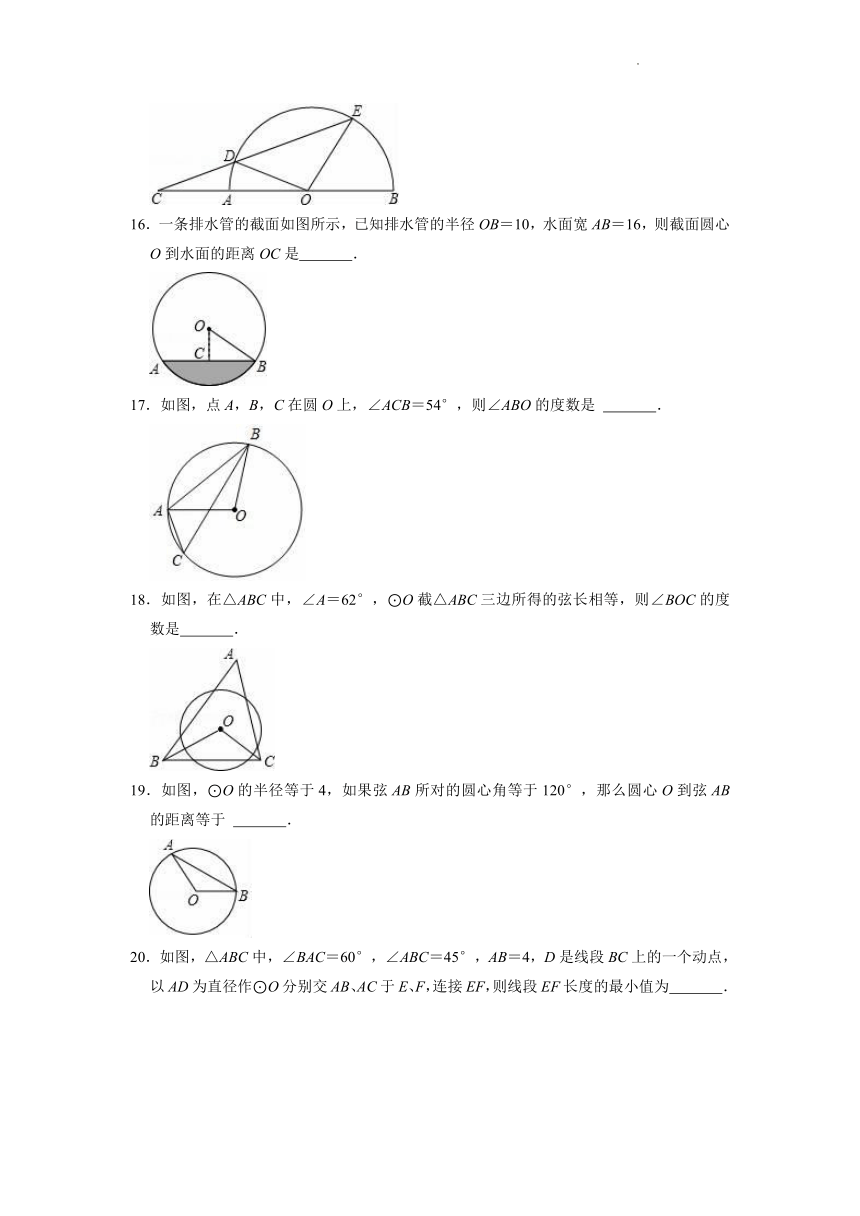
15.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
16.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是 .
17.如图,点A,B,C在圆O上,∠ACB=54°,则∠ABO的度数是 .
18.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
19.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于 .
20.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
三.解答题(共7小题,满分60分)
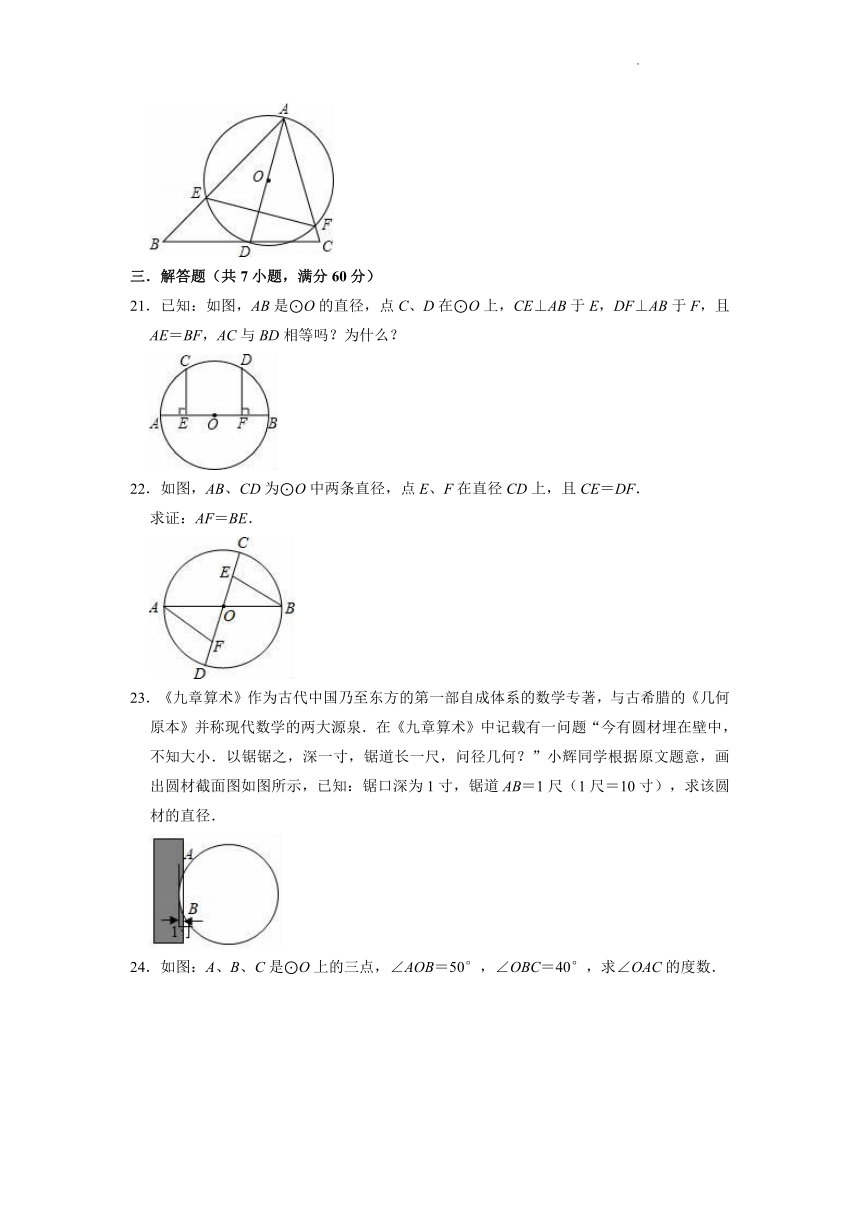
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
23.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
24.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
25.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
26.如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=2m,CD=8m,求⊙O的直径.
27.如图,OD是⊙O的半径,AB是弦,且OD⊥AB于点C连接AO并延长交⊙O于点E,若AB=8,CD=2,求⊙O半径OA的长.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
2.解:①根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以①正确.
②弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以②错误.
③圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以③正确.
④等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以④错误.
⑤根据等弧的概念,能够完全重合的两条弧叫等弧.所以⑤是正确的.
故选:C.
3.解:如图;连接OA;
根据垂径定理,得AC=BC=12cm;
Rt△OAC中,OA=13cm,AC=12cm;
根据勾股定理,得:
OC==5cm;
∴CD=OD﹣OC=8cm;
故选:A.
4.解:∵OD⊥BC,∠ABC=30°,
∴在直角三角形OBE中,
∠BOE=60°(直角三角形的两个锐角互余),即∠DOB=60°.
又∵∠DCB=∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠DCB=30°;
故选:A.
5.解:作⊙O的直径CD,连接BD,
∴∠CBD=90°,
∵∠D=∠BAC=30°,BC=12,
∴CD=2BC=24,
即⊙O的直径为24.
故选:C.
6.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为.
故选:C.
7.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
8.解:∵OA⊥OB,
∴∠AOB=90°,
由圆周角定理得,∠ACB=∠AOB=45°,
故选:D.
9.解:根据题意知,的长度为:π×1≈×3=1.5,则与拉直后铁丝N端的位置最接近的是点A.
故选:A.
10.解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故答案为:60°
12.解:∵BD=CD,
∴OD⊥BC,
在Rt△OBD中,∵OB=5,OD=3,
∴BD==4,
∴BC=2BD=8.
故答案为8.
13.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
16.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故答案为:6.
17.解:根据题意得∠AOB=2∠ACB=2×54°=108°,
∵OA=OB,
∴∠ABO=∠BAO,
∴∠ABO=(180°﹣∠AOB)=(180°﹣108°)=36°.
故答案为36°.
18.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
19.解:如图,∵圆心角∠AOB=120°,OA=OB,
∴△OAB是等腰三角形,
∵OC⊥AB,
∴∠ACO=90°,∠A=30°,
∴OC=.
故答案为:2
20.解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=4,
∴AD=BD=2,即此时圆的直径为2,
由圆周角定理可知∠EOH=∠FOH=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=×=,
由垂径定理可知EF=2EH=,
故答案为:.
三.解答题(共7小题,满分60分)
21.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
23.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
24.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
25.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
26.(1)证明:∵AB⊥CD,AB过O,
∴弧BC=弧BD,
∴∠BCD=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠ACO=∠BCD;
(2)解:∵AB⊥CD,AB过O,CD=8m,
∴CE=DE=4m,
在Rt△CEB中,由勾股定理得:BC==2(m),
∵AB为直径,AB⊥CD,
∴∠BCA=∠CEB=90°,
∵∠B=∠B,
∴△BEC∽△BCA,
∴=,
∴BA===10(m),
即⊙O的直径是10m.
27.解:∵OD⊥弦AB,AB=8,
∴AC==4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
一.选择题(共10小题,满分30分)
1.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.逐渐变大 B.逐渐变小 C.不变 D.不能确定
2.下列说法:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④长度相等的两条弧是等弧;⑤完全重合的两条弧是等弧.正确的命题有( )
A.1个 B.2个 C.3个 D.4个
3.如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,则截面上有油部分油面CD(单位:cm)等于( )
A.8cm B.9cm C.10cm D.11cm
4.如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30 B.45 C.50 D.60
5.如图,△ABC内接于⊙O,∠BAC=30°,BC=12,则⊙O的直径为( )
A.12 B.20 C.24 D.30
6.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
A.3 B. C.2.5 D.2
7.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
8.如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB等于( )
A.20° B.25° C.35° D.45°
9.东汉初年,我国的《周髀算经》里就有“径一周三”的古率,提出了圆的直径与周长之间存在一定的比例关系.将图中的半圆弧形铁丝()向右水平拉直(保持M端不动),根据该古率,与拉直后铁丝N端的位置最接近的是( )
A.点A B.点B C.点C D.点D
10.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
二.填空题(共10小题,满分30分)
11.已知弦AB的长等于⊙O的半径,弦AB所对的圆心角是 .
12.如图,⊙O的半径OA与弦BC交于点D.若OD=3,AD=2,BD=CD,则BC的长为 .
13.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
15.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
16.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是 .
17.如图,点A,B,C在圆O上,∠ACB=54°,则∠ABO的度数是 .
18.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
19.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于 .
20.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
三.解答题(共7小题,满分60分)
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
23.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
24.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
25.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
26.如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=2m,CD=8m,求⊙O的直径.
27.如图,OD是⊙O的半径,AB是弦,且OD⊥AB于点C连接AO并延长交⊙O于点E,若AB=8,CD=2,求⊙O半径OA的长.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
2.解:①根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以①正确.
②弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以②错误.
③圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以③正确.
④等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以④错误.
⑤根据等弧的概念,能够完全重合的两条弧叫等弧.所以⑤是正确的.
故选:C.
3.解:如图;连接OA;
根据垂径定理,得AC=BC=12cm;
Rt△OAC中,OA=13cm,AC=12cm;
根据勾股定理,得:
OC==5cm;
∴CD=OD﹣OC=8cm;
故选:A.
4.解:∵OD⊥BC,∠ABC=30°,
∴在直角三角形OBE中,
∠BOE=60°(直角三角形的两个锐角互余),即∠DOB=60°.
又∵∠DCB=∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠DCB=30°;
故选:A.
5.解:作⊙O的直径CD,连接BD,
∴∠CBD=90°,
∵∠D=∠BAC=30°,BC=12,
∴CD=2BC=24,
即⊙O的直径为24.
故选:C.
6.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为.
故选:C.
7.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
8.解:∵OA⊥OB,
∴∠AOB=90°,
由圆周角定理得,∠ACB=∠AOB=45°,
故选:D.
9.解:根据题意知,的长度为:π×1≈×3=1.5,则与拉直后铁丝N端的位置最接近的是点A.
故选:A.
10.解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故答案为:60°
12.解:∵BD=CD,
∴OD⊥BC,
在Rt△OBD中,∵OB=5,OD=3,
∴BD==4,
∴BC=2BD=8.
故答案为8.
13.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
16.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故答案为:6.
17.解:根据题意得∠AOB=2∠ACB=2×54°=108°,
∵OA=OB,
∴∠ABO=∠BAO,
∴∠ABO=(180°﹣∠AOB)=(180°﹣108°)=36°.
故答案为36°.
18.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
19.解:如图,∵圆心角∠AOB=120°,OA=OB,
∴△OAB是等腰三角形,
∵OC⊥AB,
∴∠ACO=90°,∠A=30°,
∴OC=.
故答案为:2
20.解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=4,
∴AD=BD=2,即此时圆的直径为2,
由圆周角定理可知∠EOH=∠FOH=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=×=,
由垂径定理可知EF=2EH=,
故答案为:.
三.解答题(共7小题,满分60分)
21.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
23.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
24.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
25.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
26.(1)证明:∵AB⊥CD,AB过O,
∴弧BC=弧BD,
∴∠BCD=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠ACO=∠BCD;
(2)解:∵AB⊥CD,AB过O,CD=8m,
∴CE=DE=4m,
在Rt△CEB中,由勾股定理得:BC==2(m),
∵AB为直径,AB⊥CD,
∴∠BCA=∠CEB=90°,
∵∠B=∠B,
∴△BEC∽△BCA,
∴=,
∴BA===10(m),
即⊙O的直径是10m.
27.解:∵OD⊥弦AB,AB=8,
∴AC==4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
