2021-2022学年华东师大版七年级下册数学第9章多边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级下册数学第9章多边形单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 18:28:34 | ||
图片预览


文档简介
2021-2022学年华东师大新版七年级下册数学《第9章 多边形》单元测试卷
一.选择题(共10小题,满分30分)
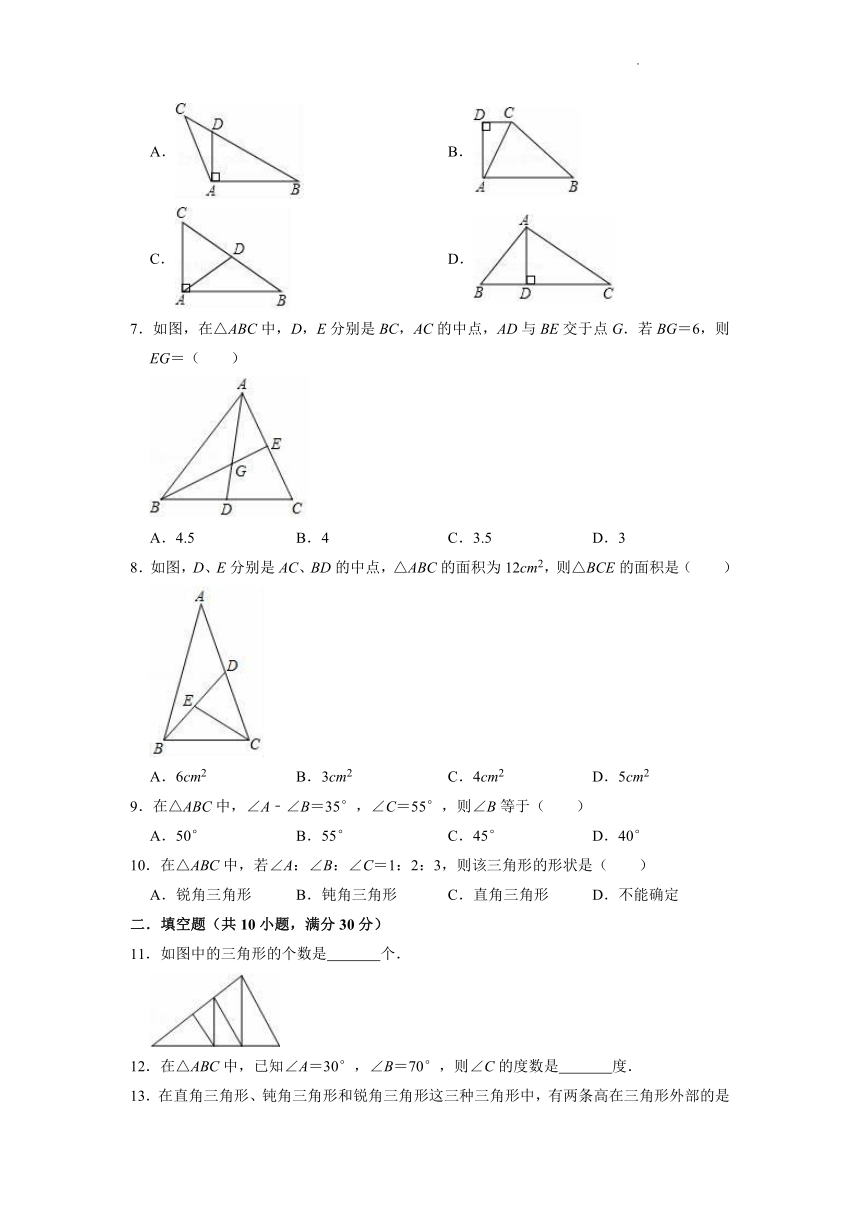
1.下面是小强用三根火柴组成的图形,其中符合三角形概念的是( )
A. B.
C. D.
2.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cm
4.如图中,三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
5.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
A.稳定性 B.灵活性 C.对称性 D.全等性
6.下列图形中AD是三角形ABC的高线的是( )
A. B.
C. D.
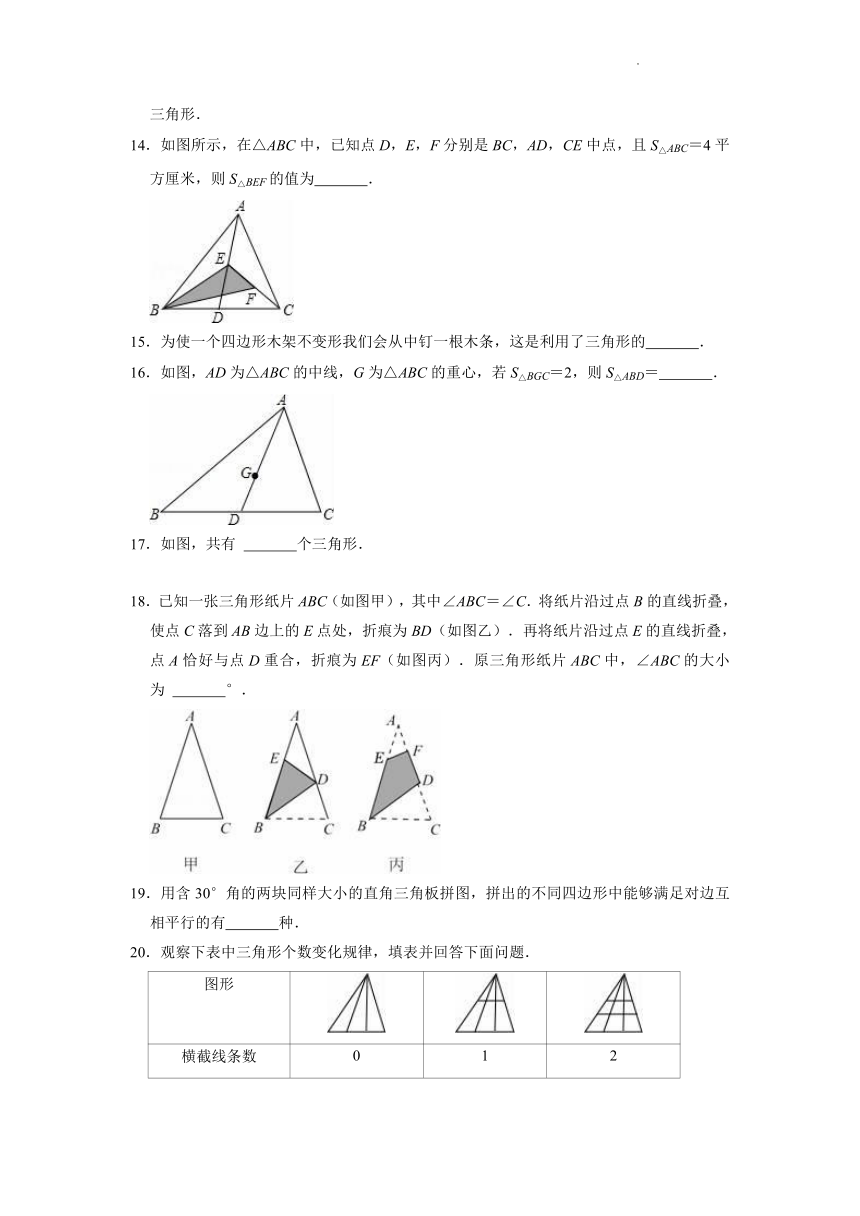
7.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE交于点G.若BG=6,则EG=( )
A.4.5 B.4 C.3.5 D.3
8.如图,D、E分别是AC、BD的中点,△ABC的面积为12cm2,则△BCE的面积是( )
A.6cm2 B.3cm2 C.4cm2 D.5cm2
9.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( )
A.50° B.55° C.45° D.40°
10.在△ABC中,若∠A:∠B:∠C=1:2:3,则该三角形的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
二.填空题(共10小题,满分30分)
11.如图中的三角形的个数是 个.
12.在△ABC中,已知∠A=30°,∠B=70°,则∠C的度数是 度.
13.在直角三角形、钝角三角形和锐角三角形这三种三角形中,有两条高在三角形外部的是 三角形.
14.如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为 .
15.为使一个四边形木架不变形我们会从中钉一根木条,这是利用了三角形的 .
16.如图,AD为△ABC的中线,G为△ABC的重心,若S△BGC=2,则S△ABD= .
17.如图,共有 个三角形.
18.已知一张三角形纸片ABC(如图甲),其中∠ABC=∠C.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为 °.
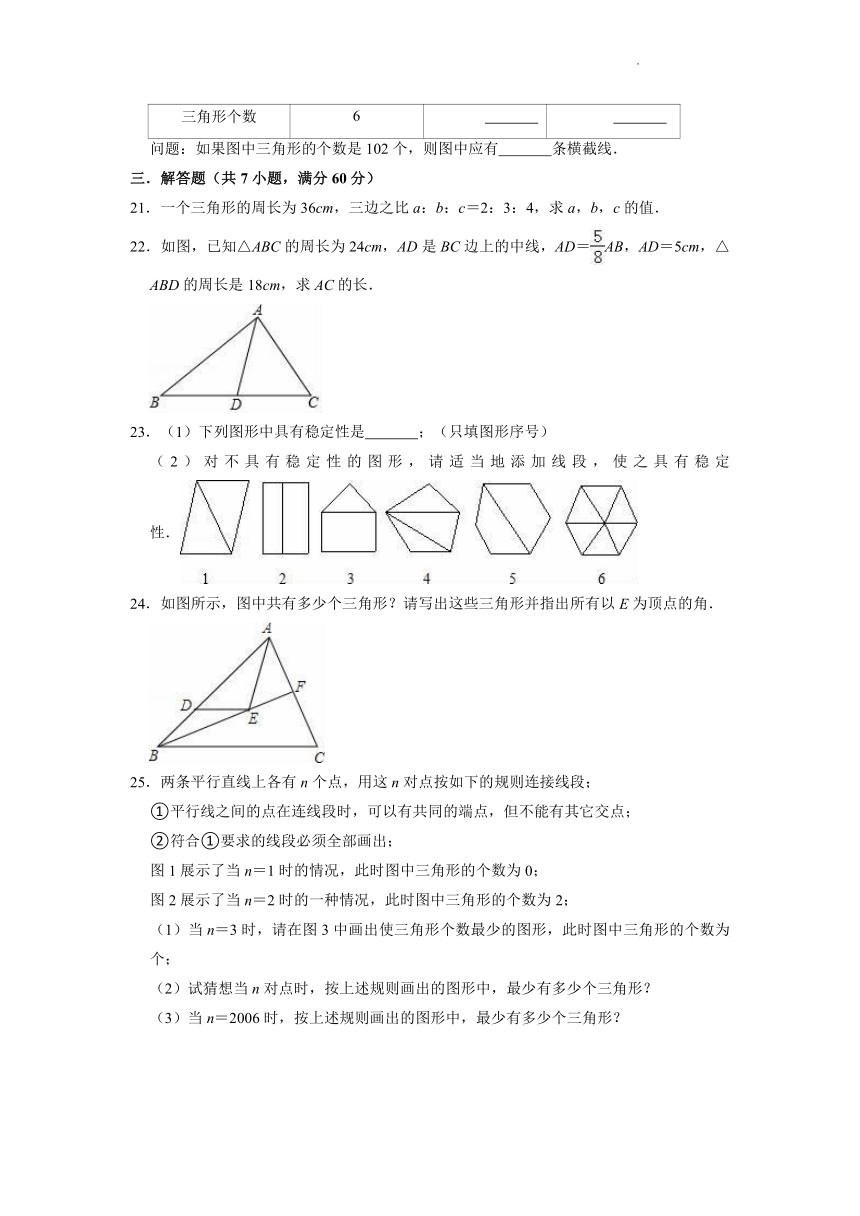
19.用含30°角的两块同样大小的直角三角板拼图,拼出的不同四边形中能够满足对边互相平行的有 种.
20.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
三.解答题(共7小题,满分60分)
21.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
22.如图,已知△ABC的周长为24cm,AD是BC边上的中线,AD=AB,AD=5cm,△ABD的周长是18cm,求AC的长.
23.(1)下列图形中具有稳定性是 ;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
25.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
26.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形;…猜测第七个图形中共有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
27.操作与探究
探索:在如图1至图3中,△ABC的面积为a.
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA、若△ACD的面积为S1,则S1= (用含a的代数式表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE、若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3)、若阴影部分的面积为S3,则S3= (用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次、可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 倍.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选:C.
2.解:A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°.故该选项正确.
故选:D.
3.解:设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x﹣1)cm.
则(x+1)+x+(x﹣1)=12,
解得:x=4,
则最短的边长是:4﹣1=3cm.
故选:B.
4.解:根据图示知,图中的三角形有:△ABE,△ABC,△DEC,△DBC,△EBC,共有5个.
故选:C.
5.解:这是利用了三角形的稳定性.故选A.
6.解:过点A作直线BC的垂线段,即画BC边上的高AD,所以画法正确的是D.
故选:D.
7.解:∵D,E分别是BC,AC的中点,AD与BE交于点G.
∴G点为△ABC的重心,
∴GE=BG=×6=3.
故选:D.
8.解:∵D是AC的中点,
∴S△BCD=S△ABC=×12=6(cm2);
∵E是BD的中点,
∴S△BCE=S△BCD=×6=3(cm2).
故选:B.
9.解:∵△ABC中,∠C=55°,
∴∠A+∠B=180°﹣∠C=180°﹣55°=125°①,
∵∠A﹣∠B=35°②,
∴①﹣②得,2∠B=90°,解得∠B=45°.
故选:C.
10.解:设∠A、∠B、∠C分别为k、2k、3k,
则k+3k+2k=180°,
∴k=30°,
∴∠C=3k=90°,
∴该三角形的形状是直角三角形,
故选:C.
二.填空题(共10小题,满分30分)
11.解:5+4=9(个)
故答案为:9.
12.解:∠C=180°﹣∠A﹣∠B=80°.
故答案为:80°.
13.解:有两条高在三角形外部的是钝角三角形.
14.解:∵D是BC的中点,
∴S△ABD=S△ACD=S△ABC=×4=2cm2,
∵E是AD的中点,
∴S△BDE=S△CDE=×2=1cm2,
∴S△BEF=(S△BDE+S△CDE)=×(1+1)=1cm2.
故答案为:1cm2.
15.解:为使一个四边形木架不变形我们会从中钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
16.解:∵G为△ABC的重心,
∴AD=2GD,
∵S△BGC=2,
∴S△ABC=6,
∵AD为△ABC的中线,
∴S△ABD=3,
故答案为:3.
17.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
18.解:设∠ABC=∠C=2α,则∠A=180°﹣∠ABC﹣∠C=180°﹣4α,
由折叠得,∠BED=∠C=2α,∠ADE=∠A=180°﹣4α,
∵∠BED是△AED的外角,
∴∠BED=∠A+∠ADE,
∴2α=180°﹣4α+180°﹣4α,
解得:α=36°,
∴∠ABC=72°,
故答案为:72.
19.解:30°角与60°的角拼在一起,30°角与90°的角拼在一起,90°的角与60°的角拼在一起,共3种.
20.解:表格中应是12,18;
有n条横线的时候,有(6+6n)个三角形,
∴6+6n=102,n=16,有16条横线.
故答案为:12,18;16.
三.解答题(共7小题,满分60分)
21.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
22.解:∵AD=AB,AD=5cm,
∴AB=8cm.
又∵△ABD的周长是18cm,
∴BD=5cm.
又∵D是BC的中点,
∴BC=2BD=10cm.
又∵△ABC的周长为24cm,
∴AC=24﹣8﹣10=6cm.
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
25.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
26.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
27.解:(1)∵CD=BC,△ABC的面积为a,△ABC与△ACD的高相等,
∴S1=S△ABC=a;
(2)分别过A、E作AG⊥BD,EF⊥BD,G、F为垂足,则AG∥EF,
∵A为CE的中点,∴AG=EF,
∵BC=CD,
∴S2=2S1=2a;
(3)∵△BDF的边长BD是△ABC边长BC的2倍,两三角形的两边互为另一三角形两边的延长线,
∴S△BDF=2S△ABC,
∵△ABC面积为a,∴S△BDF=2a.
同理可得,S△ECD=2a,S△AEF=2a,∴S3=S△BDF+S△ECD+S△AEF=2a+2a+2a=6a.
∵S3=S△BDF+S△ECD+S△AEF=6a,
∴S△EDF=S3+S△ABC=6a+a=7a,
∴==7,
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
一.选择题(共10小题,满分30分)
1.下面是小强用三根火柴组成的图形,其中符合三角形概念的是( )
A. B.
C. D.
2.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cm
4.如图中,三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
5.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
A.稳定性 B.灵活性 C.对称性 D.全等性
6.下列图形中AD是三角形ABC的高线的是( )
A. B.
C. D.
7.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE交于点G.若BG=6,则EG=( )
A.4.5 B.4 C.3.5 D.3
8.如图,D、E分别是AC、BD的中点,△ABC的面积为12cm2,则△BCE的面积是( )
A.6cm2 B.3cm2 C.4cm2 D.5cm2
9.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( )
A.50° B.55° C.45° D.40°
10.在△ABC中,若∠A:∠B:∠C=1:2:3,则该三角形的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
二.填空题(共10小题,满分30分)
11.如图中的三角形的个数是 个.
12.在△ABC中,已知∠A=30°,∠B=70°,则∠C的度数是 度.
13.在直角三角形、钝角三角形和锐角三角形这三种三角形中,有两条高在三角形外部的是 三角形.
14.如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为 .
15.为使一个四边形木架不变形我们会从中钉一根木条,这是利用了三角形的 .
16.如图,AD为△ABC的中线,G为△ABC的重心,若S△BGC=2,则S△ABD= .
17.如图,共有 个三角形.
18.已知一张三角形纸片ABC(如图甲),其中∠ABC=∠C.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为 °.
19.用含30°角的两块同样大小的直角三角板拼图,拼出的不同四边形中能够满足对边互相平行的有 种.
20.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
三.解答题(共7小题,满分60分)
21.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
22.如图,已知△ABC的周长为24cm,AD是BC边上的中线,AD=AB,AD=5cm,△ABD的周长是18cm,求AC的长.
23.(1)下列图形中具有稳定性是 ;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
25.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
26.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形;…猜测第七个图形中共有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
27.操作与探究
探索:在如图1至图3中,△ABC的面积为a.
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA、若△ACD的面积为S1,则S1= (用含a的代数式表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE、若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3)、若阴影部分的面积为S3,则S3= (用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次、可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 倍.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选:C.
2.解:A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°.故该选项正确.
故选:D.
3.解:设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x﹣1)cm.
则(x+1)+x+(x﹣1)=12,
解得:x=4,
则最短的边长是:4﹣1=3cm.
故选:B.
4.解:根据图示知,图中的三角形有:△ABE,△ABC,△DEC,△DBC,△EBC,共有5个.
故选:C.
5.解:这是利用了三角形的稳定性.故选A.
6.解:过点A作直线BC的垂线段,即画BC边上的高AD,所以画法正确的是D.
故选:D.
7.解:∵D,E分别是BC,AC的中点,AD与BE交于点G.
∴G点为△ABC的重心,
∴GE=BG=×6=3.
故选:D.
8.解:∵D是AC的中点,
∴S△BCD=S△ABC=×12=6(cm2);
∵E是BD的中点,
∴S△BCE=S△BCD=×6=3(cm2).
故选:B.
9.解:∵△ABC中,∠C=55°,
∴∠A+∠B=180°﹣∠C=180°﹣55°=125°①,
∵∠A﹣∠B=35°②,
∴①﹣②得,2∠B=90°,解得∠B=45°.
故选:C.
10.解:设∠A、∠B、∠C分别为k、2k、3k,
则k+3k+2k=180°,
∴k=30°,
∴∠C=3k=90°,
∴该三角形的形状是直角三角形,
故选:C.
二.填空题(共10小题,满分30分)
11.解:5+4=9(个)
故答案为:9.
12.解:∠C=180°﹣∠A﹣∠B=80°.
故答案为:80°.
13.解:有两条高在三角形外部的是钝角三角形.
14.解:∵D是BC的中点,
∴S△ABD=S△ACD=S△ABC=×4=2cm2,
∵E是AD的中点,
∴S△BDE=S△CDE=×2=1cm2,
∴S△BEF=(S△BDE+S△CDE)=×(1+1)=1cm2.
故答案为:1cm2.
15.解:为使一个四边形木架不变形我们会从中钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
16.解:∵G为△ABC的重心,
∴AD=2GD,
∵S△BGC=2,
∴S△ABC=6,
∵AD为△ABC的中线,
∴S△ABD=3,
故答案为:3.
17.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
18.解:设∠ABC=∠C=2α,则∠A=180°﹣∠ABC﹣∠C=180°﹣4α,
由折叠得,∠BED=∠C=2α,∠ADE=∠A=180°﹣4α,
∵∠BED是△AED的外角,
∴∠BED=∠A+∠ADE,
∴2α=180°﹣4α+180°﹣4α,
解得:α=36°,
∴∠ABC=72°,
故答案为:72.
19.解:30°角与60°的角拼在一起,30°角与90°的角拼在一起,90°的角与60°的角拼在一起,共3种.
20.解:表格中应是12,18;
有n条横线的时候,有(6+6n)个三角形,
∴6+6n=102,n=16,有16条横线.
故答案为:12,18;16.
三.解答题(共7小题,满分60分)
21.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
22.解:∵AD=AB,AD=5cm,
∴AB=8cm.
又∵△ABD的周长是18cm,
∴BD=5cm.
又∵D是BC的中点,
∴BC=2BD=10cm.
又∵△ABC的周长为24cm,
∴AC=24﹣8﹣10=6cm.
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
25.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
26.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
27.解:(1)∵CD=BC,△ABC的面积为a,△ABC与△ACD的高相等,
∴S1=S△ABC=a;
(2)分别过A、E作AG⊥BD,EF⊥BD,G、F为垂足,则AG∥EF,
∵A为CE的中点,∴AG=EF,
∵BC=CD,
∴S2=2S1=2a;
(3)∵△BDF的边长BD是△ABC边长BC的2倍,两三角形的两边互为另一三角形两边的延长线,
∴S△BDF=2S△ABC,
∵△ABC面积为a,∴S△BDF=2a.
同理可得,S△ECD=2a,S△AEF=2a,∴S3=S△BDF+S△ECD+S△AEF=2a+2a+2a=6a.
∵S3=S△BDF+S△ECD+S△AEF=6a,
∴S△EDF=S3+S△ABC=6a+a=7a,
∴==7,
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
