2021-2022学年人教版九年级数学下册第二十九章 投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章 投影与视图单元测试训练卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 272.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 00:00:00 | ||
图片预览



文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
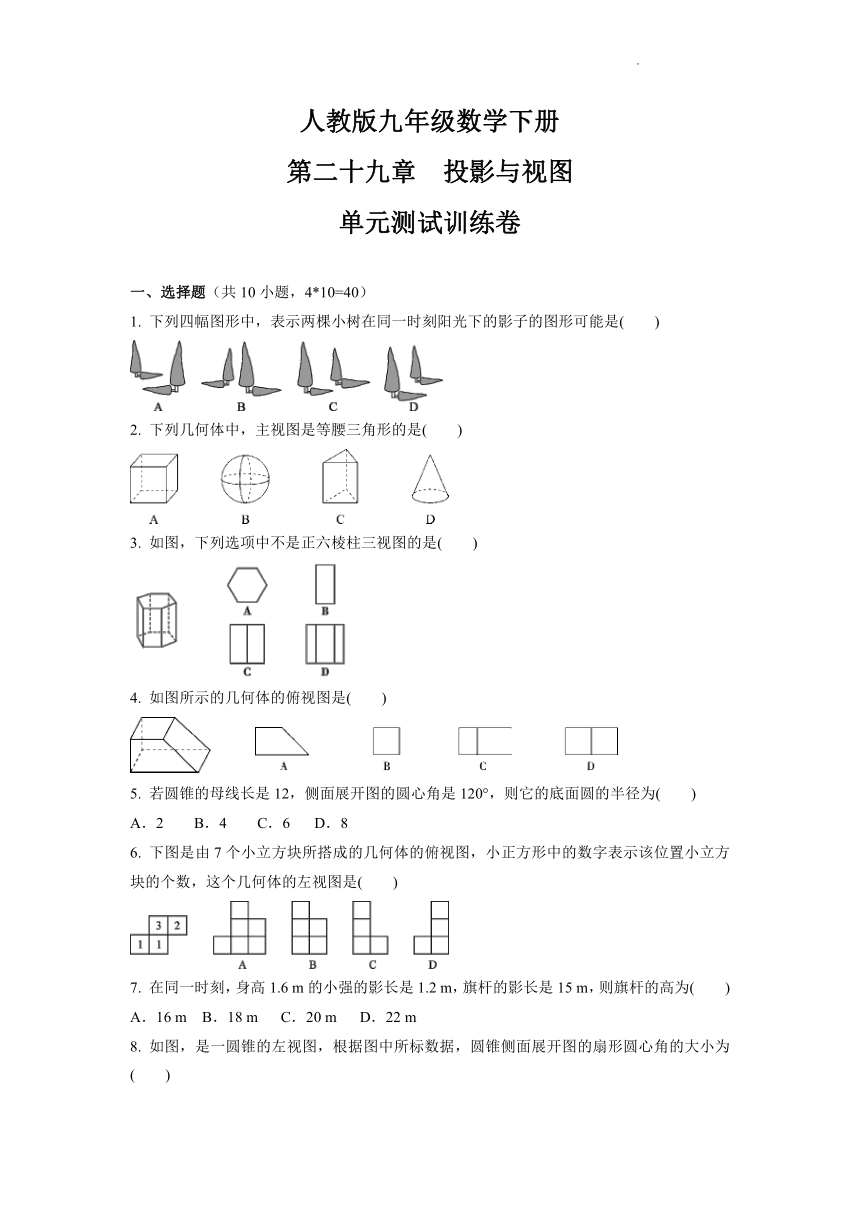
1. 下列四幅图形中,表示两棵小树在同一时刻阳光下的影子的图形可能是( )
2. 下列几何体中,主视图是等腰三角形的是( )
3. 如图,下列选项中不是正六棱柱三视图的是( )
4. 如图所示的几何体的俯视图是( )
5. 若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
A.2 B.4 C.6 D.8
6. 下图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是( )
7. 在同一时刻,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为( )
A.16 m B.18 m C.20 m D.22 m
8. 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
9.如图,将正方体相邻的两个面上分别画出3×3的正方形网格,并分别用图形“”和“”在网格内的交点处做上标记,则该正方体的表面展开图是( )
10. 如图,夜晚,小亮从A经过路灯C的正下方沿直线走到点B,他的影子y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为( )
二.填空题(共6小题,4*6=24)
11. 猜谜语:“横看是圆,侧看是圆,远看是圆,近看是圆,高看是圆,低看是圆,上看、下看、左看、右看都是圆.”谜底是__ _.
12. 一张矩形的纸板(不考虑厚度,不折叠),其正投影可能是____________.
①矩形;②平行四边形;③线段;④三角形;⑤任意四边形;⑥点.
13. 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2m,太阳光线与地面的夹角∠ACD=60°,则AB的长为________m.
14. 如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为________m.
15.如图所示,若一个圆柱的侧面展开图是长、宽分别为4π、2π的矩形,则该圆柱的底面圆的半径为________.
16.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则组成这个几何体的小立方体的个数可能是____________.
三.解答题(共5小题, 56分)
17.(6分) 如图,几何体的三种视图有无错误?如果有,请改正.
18.(8分) 一个几何体的三视图如图所示,其俯视图是一个菱形.
(1)请写出符合这个几何体的名称;
(2)求这个几何体的表面积.
19.(8分) 一位同学想利用有关知识测旗杆的高度,如图,他在某一时刻测得高为0.5 m的小木棒的影子长为0.3 m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0 m,又测地面部分的影长BC=3.0 m,你能根据上述数据帮他测出旗杆的高度吗?
20.(10分) 某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
(1)请在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=6米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.
21.(12分) 如图①,王华同学在晚上由路灯AC走向路灯BD,当她走到点P时,发现身后她影子的顶部刚好接触到路灯AC的底部,当她向前再走12 m到达Q点时,发现身前她影子的顶部刚好接触到路灯BD的底部,已知王华同学的身高是1.6 m,两个路灯的高度都是9.6 m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,如图②,她在路灯AC下的影子长BF是多少?
22.(12分) 如图,在晚上,身高是1.6 m的王磊由路灯A的正下方走向路灯B时,当他走到点P时,发现身后他的影子的顶部刚好接触到路灯A的底部,当他再向前步行12 m到达点Q时,发现身前他的影子的顶部刚好接触到路灯B的底部,已知两个路灯的高度都是9.6 m.
(1)求两个路灯之间的距离;
(2)当王磊走到路灯B的正下方时,他在路灯A下的影长是多少?
参考答案
1-5DDBDB 6-10CCBCA
11.球
12.①②③
13.
14.12
15. 1或2
16.5或6或7
17. 解:主视图对,左视图错,俯视图错,如图所示.
18.解:(1)这个几何体是直四棱柱
(2)∵俯视图是菱形,∴可求得底面菱形边长为2.5 cm,上、下底面积和为6×2=12 cm2,侧面积为2.5×4×8=80 cm2,∴这个几何体的表面积92 cm2
19.解:作DE⊥AB于点E,那么四边形BCDE是矩形,∴BE=CD=1.0 m,DE=BC=3.0 m,∴=,∴AE=5(m),∴AB=AE+BE=6(m)
20. 解:(1)如图:
(2)设木杆AB的影长BF为x米,由题意得=,解得x=8,则木杆AB的影长是8米
21. 解:(1)由题易知AP=BQ, 设AP=BQ=x m.∵MP∥BD,∴△APM∽△ABD, ∴=,∴=,解得x=3,∴AB=2×3+12=18(m).答:两个路灯之间的距离为18 m.
(2)设BF=y m.∵BE∥AC,∴△FEB∽△FCA,∴=,即=,解得y=3.6.
22.解:(1)如图,∵点D,M,A和点C,N,B分别共线,∴可分别连接点D,M,A和C,N,B.分析题意知AP=BQ,设AP=QB=x m,由题意可知,Rt△BNQ∽Rt△BCA,∴=,∴=,解得x=3.又∵PQ=12 m,∴AB=12+6=18(m).故两个路灯之间的距离为18 m
(2)王磊走到路灯B的正下方时,设他在路灯A下的影长BE=y m,由Rt△EFB∽Rt△ECA,可得=,解得y=3.6,即当王磊走到路灯B的正下方时,他在路灯A下的影长是3.6 m
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列四幅图形中,表示两棵小树在同一时刻阳光下的影子的图形可能是( )
2. 下列几何体中,主视图是等腰三角形的是( )
3. 如图,下列选项中不是正六棱柱三视图的是( )
4. 如图所示的几何体的俯视图是( )
5. 若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
A.2 B.4 C.6 D.8
6. 下图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是( )
7. 在同一时刻,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为( )
A.16 m B.18 m C.20 m D.22 m
8. 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
9.如图,将正方体相邻的两个面上分别画出3×3的正方形网格,并分别用图形“”和“”在网格内的交点处做上标记,则该正方体的表面展开图是( )
10. 如图,夜晚,小亮从A经过路灯C的正下方沿直线走到点B,他的影子y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为( )
二.填空题(共6小题,4*6=24)
11. 猜谜语:“横看是圆,侧看是圆,远看是圆,近看是圆,高看是圆,低看是圆,上看、下看、左看、右看都是圆.”谜底是__ _.
12. 一张矩形的纸板(不考虑厚度,不折叠),其正投影可能是____________.
①矩形;②平行四边形;③线段;④三角形;⑤任意四边形;⑥点.
13. 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2m,太阳光线与地面的夹角∠ACD=60°,则AB的长为________m.
14. 如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为________m.
15.如图所示,若一个圆柱的侧面展开图是长、宽分别为4π、2π的矩形,则该圆柱的底面圆的半径为________.
16.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则组成这个几何体的小立方体的个数可能是____________.
三.解答题(共5小题, 56分)
17.(6分) 如图,几何体的三种视图有无错误?如果有,请改正.
18.(8分) 一个几何体的三视图如图所示,其俯视图是一个菱形.
(1)请写出符合这个几何体的名称;
(2)求这个几何体的表面积.
19.(8分) 一位同学想利用有关知识测旗杆的高度,如图,他在某一时刻测得高为0.5 m的小木棒的影子长为0.3 m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0 m,又测地面部分的影长BC=3.0 m,你能根据上述数据帮他测出旗杆的高度吗?
20.(10分) 某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
(1)请在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=6米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.
21.(12分) 如图①,王华同学在晚上由路灯AC走向路灯BD,当她走到点P时,发现身后她影子的顶部刚好接触到路灯AC的底部,当她向前再走12 m到达Q点时,发现身前她影子的顶部刚好接触到路灯BD的底部,已知王华同学的身高是1.6 m,两个路灯的高度都是9.6 m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,如图②,她在路灯AC下的影子长BF是多少?
22.(12分) 如图,在晚上,身高是1.6 m的王磊由路灯A的正下方走向路灯B时,当他走到点P时,发现身后他的影子的顶部刚好接触到路灯A的底部,当他再向前步行12 m到达点Q时,发现身前他的影子的顶部刚好接触到路灯B的底部,已知两个路灯的高度都是9.6 m.
(1)求两个路灯之间的距离;
(2)当王磊走到路灯B的正下方时,他在路灯A下的影长是多少?
参考答案
1-5DDBDB 6-10CCBCA
11.球
12.①②③
13.
14.12
15. 1或2
16.5或6或7
17. 解:主视图对,左视图错,俯视图错,如图所示.
18.解:(1)这个几何体是直四棱柱
(2)∵俯视图是菱形,∴可求得底面菱形边长为2.5 cm,上、下底面积和为6×2=12 cm2,侧面积为2.5×4×8=80 cm2,∴这个几何体的表面积92 cm2
19.解:作DE⊥AB于点E,那么四边形BCDE是矩形,∴BE=CD=1.0 m,DE=BC=3.0 m,∴=,∴AE=5(m),∴AB=AE+BE=6(m)
20. 解:(1)如图:
(2)设木杆AB的影长BF为x米,由题意得=,解得x=8,则木杆AB的影长是8米
21. 解:(1)由题易知AP=BQ, 设AP=BQ=x m.∵MP∥BD,∴△APM∽△ABD, ∴=,∴=,解得x=3,∴AB=2×3+12=18(m).答:两个路灯之间的距离为18 m.
(2)设BF=y m.∵BE∥AC,∴△FEB∽△FCA,∴=,即=,解得y=3.6.
22.解:(1)如图,∵点D,M,A和点C,N,B分别共线,∴可分别连接点D,M,A和C,N,B.分析题意知AP=BQ,设AP=QB=x m,由题意可知,Rt△BNQ∽Rt△BCA,∴=,∴=,解得x=3.又∵PQ=12 m,∴AB=12+6=18(m).故两个路灯之间的距离为18 m
(2)王磊走到路灯B的正下方时,设他在路灯A下的影长BE=y m,由Rt△EFB∽Rt△ECA,可得=,解得y=3.6,即当王磊走到路灯B的正下方时,他在路灯A下的影长是3.6 m
