2021-2022学年北师大版八年级数学下册2.1不等关系课件(18张)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册2.1不等关系课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
2.1 不等关系
温故知新
我们学过等式,请问什么是等式?
表示相等关系的式子叫等式。
我们知道相等关系的量可以利用等式来描述;同时,现实生活中还存在许多反映不等关系的量。比如,研究表明同学们每天睡觉的时间要不少于8小时;数学考试中合格的分数要不低于72分。
学习目标
1. 理解不等式的意义,学会用不等式解决实际问题(重点)
2. 能根据条件列出不等式(难点)
新知探究
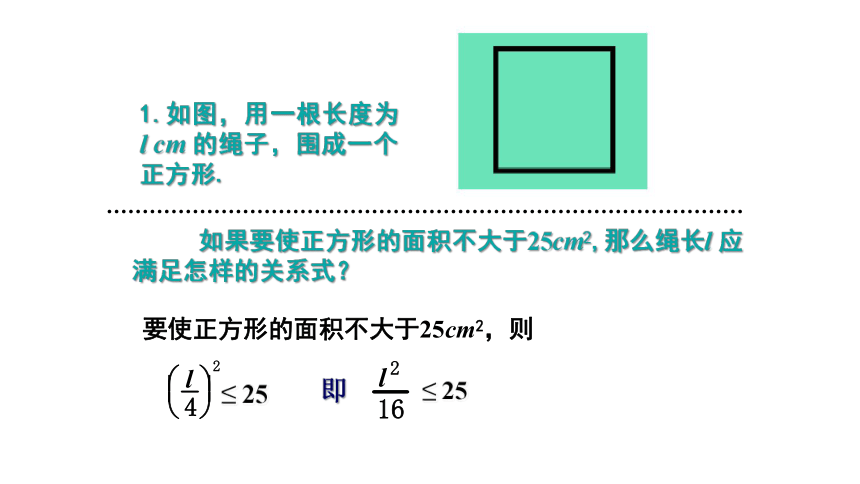
1.如图,用一根长度为l cm 的绳子,围成一个正方形.
如果要使正方形的面积不大于25cm2,那么绳长l 应满足怎样的关系式?
要使正方形的面积不大于25cm2,则
即
≤ 25
≤ 25
如果要使圆的面积不小于100cm2,那么绳长l 应满足怎样的关系式?
2.如图,用一根长度为l cm 的绳子,围成一个圆.
≥100
即
≥100
要使圆的面积不小于100cm2,则
3.当l =8时,正方形和圆的面积哪个大 当l =12时呢?改变l 的取值试一试.由此你能得到什么猜想?
我们可以猜想,用长度均为lcm的两根绳子分别围成
一个正方形和圆,无论l取何值,圆的面积总大于正方形的面积,即
>
(1)铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160㎝,设行李的长、宽、高分别为a㎝、b㎝、c㎝,请你列出行李的长宽高满足的关系式
(2)通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5m的地方为测量部位。某树栽种时的树围为6㎝,以后10年内每年增加约3㎝,设经过x年后这棵树的树围超过30㎝,请你列出x满足的关系式。
解:6+3x>30
解:a+b+c ≤ 160
做一做
一般地,用符号“<”(或“≤”)、“>”(或“≥”)、“≠”连接的式子叫做不等式。
议一议:
观察上面得到的关系式,它们有什么共同特点?
注意:用“≠”连接的式子也是不等式
注意:
“不大于” 指的是 “ ”,
通常用 符号 “ ” 表示.
类似地,“不小于”指的是“大于或等于”.
通常用符号“≥”表示。(读作:“大于或等于”).
小于或等于
≤
例如,x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”).
关键词语 ①大 于 ②比…大③超 过 ①小 于 ②比…小③低 于 ①不大于 ②不超过 ③至 多 ①不小于 ②不低于 ③至 少 正数 负数 非负数 非正数
不等号
常用的表示不等关系的关键词语及对应的不等号
第二类:明确表明数量的范围特征
>
<
≤
≥
>0
<0
≥0
≤0
第一类:明确表明数量的不等关系
易错易混点点拨
练一练:
1. 用不等式表示:
(1)a是正数;
(2)x与5的和是负数;
(3)m的一半不大于10;
(4)x的一半与1的差是非负数.
2. 设“●”、“▲”、“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列应为( )
A.■、●、▲ B.■、▲、●
C.▲、●、■ D.▲、■、●
课堂小结
数学建模、类比等式
不等式
一要注意 “负数”、“非负数”、“不大于”、“不小于”等关键词语的含义.
二要注意仔细审题,正确列出不等式.
三要注意实际生活中的不等关系.
三个注意:
一个概念:
二种思想:
付出≥收获
现阶段:我们能做的就是努力付出,等待收获!!
当堂检测
2.1 不等关系
温故知新
我们学过等式,请问什么是等式?
表示相等关系的式子叫等式。
我们知道相等关系的量可以利用等式来描述;同时,现实生活中还存在许多反映不等关系的量。比如,研究表明同学们每天睡觉的时间要不少于8小时;数学考试中合格的分数要不低于72分。
学习目标
1. 理解不等式的意义,学会用不等式解决实际问题(重点)
2. 能根据条件列出不等式(难点)
新知探究
1.如图,用一根长度为l cm 的绳子,围成一个正方形.
如果要使正方形的面积不大于25cm2,那么绳长l 应满足怎样的关系式?
要使正方形的面积不大于25cm2,则
即
≤ 25
≤ 25
如果要使圆的面积不小于100cm2,那么绳长l 应满足怎样的关系式?
2.如图,用一根长度为l cm 的绳子,围成一个圆.
≥100
即
≥100
要使圆的面积不小于100cm2,则
3.当l =8时,正方形和圆的面积哪个大 当l =12时呢?改变l 的取值试一试.由此你能得到什么猜想?
我们可以猜想,用长度均为lcm的两根绳子分别围成
一个正方形和圆,无论l取何值,圆的面积总大于正方形的面积,即
>
(1)铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160㎝,设行李的长、宽、高分别为a㎝、b㎝、c㎝,请你列出行李的长宽高满足的关系式
(2)通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5m的地方为测量部位。某树栽种时的树围为6㎝,以后10年内每年增加约3㎝,设经过x年后这棵树的树围超过30㎝,请你列出x满足的关系式。
解:6+3x>30
解:a+b+c ≤ 160
做一做
一般地,用符号“<”(或“≤”)、“>”(或“≥”)、“≠”连接的式子叫做不等式。
议一议:
观察上面得到的关系式,它们有什么共同特点?
注意:用“≠”连接的式子也是不等式
注意:
“不大于” 指的是 “ ”,
通常用 符号 “ ” 表示.
类似地,“不小于”指的是“大于或等于”.
通常用符号“≥”表示。(读作:“大于或等于”).
小于或等于
≤
例如,x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”).
关键词语 ①大 于 ②比…大③超 过 ①小 于 ②比…小③低 于 ①不大于 ②不超过 ③至 多 ①不小于 ②不低于 ③至 少 正数 负数 非负数 非正数
不等号
常用的表示不等关系的关键词语及对应的不等号
第二类:明确表明数量的范围特征
>
<
≤
≥
>0
<0
≥0
≤0
第一类:明确表明数量的不等关系
易错易混点点拨
练一练:
1. 用不等式表示:
(1)a是正数;
(2)x与5的和是负数;
(3)m的一半不大于10;
(4)x的一半与1的差是非负数.
2. 设“●”、“▲”、“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列应为( )
A.■、●、▲ B.■、▲、●
C.▲、●、■ D.▲、■、●
课堂小结
数学建模、类比等式
不等式
一要注意 “负数”、“非负数”、“不大于”、“不小于”等关键词语的含义.
二要注意仔细审题,正确列出不等式.
三要注意实际生活中的不等关系.
三个注意:
一个概念:
二种思想:
付出≥收获
现阶段:我们能做的就是努力付出,等待收获!!
当堂检测
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
