9.1.2三角形的内角和与外角和 课件(共28张PPT)
文档属性
| 名称 | 9.1.2三角形的内角和与外角和 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 06:29:09 | ||
图片预览








文档简介
(共28张PPT)
2022年春华师大版数学
七年级下册数学精品课件
三角形的内角和与外角和
学习目标
掌握三角形的内角和定理、三角形外角的性质,理解直角三角形的两个锐角互余的性质.
会用三角形的内角与外角的性质来进行相关计算或比较.
⒈我们学行线的哪些性质呢?
⑴两直线平行,同位角相等.
⑵两直线平行,内错角相等.
⑶两直线平行,同旁内角互补.
如果a∥b, 则 ∠1 = ∠2
则 ∠1 = ∠3
则 ∠1+∠4=180°
复习回顾
2.请同学们回忆上一节三角形按角分类分为哪几类?
思考:锐角三角形、直角三角形、钝角三角形的三角之和有什么共同特点?
锐角三角形;
直角三角形;
钝角三角形.
你是怎样知道的呢?
共同特点:三角形的内角和等于180°.
复习回顾
你有什么办法可以验证它呢
方法一:剪拼法.把三个角拼在一起试试看?
探索1.三角形的内角和.
知识精讲
1
2
3
2
1
图1
1
2
3
2
3
图2
2
3
1
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
知识精讲
证明:作CE∥AB ,并延长BC到D,
∴∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵∠1+ ∠2+ ∠ACB=180° (平角定义)
∴∠A+ ∠B + ∠ACB=180° (等量代换)
2
1
2
3
1
已知:∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
2
1
E
D
C
B
A
知识精讲
F
2
1
E
C
B
A
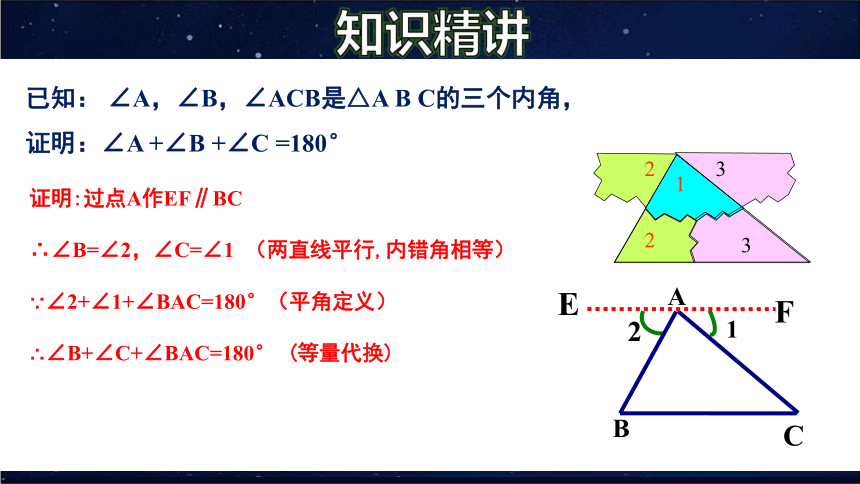
证明:过点A作EF∥BC
∴∠B=∠2,∠C=∠1 (两直线平行,内错角相等)∵∠2+∠1+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180° (等量代换)
已知: ∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
1
2
3
3
2
知识精讲
三角形的内角和定理
文字语言:三角形的内角和等于180°
符号语言:
∵ ∠A、∠B、∠C是△ABC的三个内角
∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)
直角三角的两个锐角互余
知识精讲
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.
在平面几何里,辅助线通常画成虚线.
为了证明三个角的和为180°,转化为一个平角,这种转化思想是数学中的常用方法.
知识精讲
1.在△ABC中,∠A=35°,∠ B=43 ° 则∠C= .
2.在△ABC中, ∠A :∠B:∠C=2:3:4,则∠A = ∠ B= . ∠ C= .
3.一个三角形中最多有 个直角?为什么?
4.一个三角形中最多有 个钝角?为什么?
5.一个三角形中至少有 个锐角?为什么?
102 °
80 °
60 °
40 °
2
1
1
针对练习
700
800
350
300
700
6.∠C = ( ) , ∠E = ( ) , ∠J = ( ).
30°
115°
20°
针对练习
探索2:三角形的外角与内角有什么关系呢?
思考:三角形的一个外角与相邻的内角有什么关系呢?
∠ACD(外角)+∠ACB(相邻的内角)=180 (互补)
思考:三角形的一个外角与不相邻的两个内角又有什么关系呢?
外角
相邻的内角
不相邻的内角
知识精讲
在一张白纸上画出如图所示的图形,然后把 ∠1、∠2剪下拼在一起,放到∠ 4上,看看会出现什么结果?
发现: ∠1+∠2=∠4
为什么?
知识精讲
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
A
B
C
知识精讲
方法1
2
1
E
D
C
B
A
证明:作CE∥AB,并延长BC到D
∴∠1= ∠A ∠2= ∠B
∴∠1+ ∠2= ∠A+ ∠B
∵ ∠1+ ∠2= ∠ACD,
∴ ∠ACD= ∠A+ ∠B
方法2
知识精讲
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的外角大于任何一个与它不相邻的内角。
∠ACD= ∠ A+ ∠ B
∠ ACD+ ∠ ACB=180°
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
外角+相邻的内角=180
知识精讲
与三角形每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和,如图所示∠1+∠2+∠3就是三角形外角和.
三角形外角和的定义:
(
1
知识精讲
∠1+ =180° ∠2+ =180° ∠3+ =180°
三式相加可以得到
∠1+∠2+∠3+ + + = 。 ①
而 ∠ACB+∠BAC+∠ABC=180° ②
由①②比较得到
∠1+∠2+∠3=360°
(
1
如图所示
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
∠ACB
540°
由此可知,三角形的外角和是
360°
知识精讲
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
解:(1)∵∠ADC是△ABD的外角(已知)
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等于与它不相邻的两个内角之和)
又∵∠B=∠BAD(已知)
∴∠B=80° =40°(等量代换)
典例解析
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
典例解析
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
1.判断
(1)三角形越大,它的内角和就越大。( )
(2) 一个三角形的三个内角度数是:70°、54°、45°。( )
(3)一个三角形中最多只有一个钝角或直角( )
(4) 一个三角形至少有两个锐角( )
(5)三角形的任何一个外角都大于其内角。( )
×
×
×
√
√
达标检测
2.判断∠1与∠3的大小,并说明理由。
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
解:∠3 > ∠1
达标检测
3.已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数.
(三角形内角和定理)
解:设∠A=x,则∠ABC=∠C=2x
∴x+2x+2x= 180°
解得x=36
∴∠C=2×36°=72°
∴∠DBC=180°-90°-72°(三角形内角和定理)
在△BDC中,∵∠BDC=90° (三角形高的定义)
∴∠DBC=18°
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
三角形的内角和与外角和
学习目标
掌握三角形的内角和定理、三角形外角的性质,理解直角三角形的两个锐角互余的性质.
会用三角形的内角与外角的性质来进行相关计算或比较.
⒈我们学行线的哪些性质呢?
⑴两直线平行,同位角相等.
⑵两直线平行,内错角相等.
⑶两直线平行,同旁内角互补.
如果a∥b, 则 ∠1 = ∠2
则 ∠1 = ∠3
则 ∠1+∠4=180°
复习回顾
2.请同学们回忆上一节三角形按角分类分为哪几类?
思考:锐角三角形、直角三角形、钝角三角形的三角之和有什么共同特点?
锐角三角形;
直角三角形;
钝角三角形.
你是怎样知道的呢?
共同特点:三角形的内角和等于180°.
复习回顾
你有什么办法可以验证它呢
方法一:剪拼法.把三个角拼在一起试试看?
探索1.三角形的内角和.
知识精讲
1
2
3
2
1
图1
1
2
3
2
3
图2
2
3
1
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
知识精讲
证明:作CE∥AB ,并延长BC到D,
∴∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵∠1+ ∠2+ ∠ACB=180° (平角定义)
∴∠A+ ∠B + ∠ACB=180° (等量代换)
2
1
2
3
1
已知:∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
2
1
E
D
C
B
A
知识精讲
F
2
1
E
C
B
A
证明:过点A作EF∥BC
∴∠B=∠2,∠C=∠1 (两直线平行,内错角相等)∵∠2+∠1+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180° (等量代换)
已知: ∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
1
2
3
3
2
知识精讲
三角形的内角和定理
文字语言:三角形的内角和等于180°
符号语言:
∵ ∠A、∠B、∠C是△ABC的三个内角
∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)
直角三角的两个锐角互余
知识精讲
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.
在平面几何里,辅助线通常画成虚线.
为了证明三个角的和为180°,转化为一个平角,这种转化思想是数学中的常用方法.
知识精讲
1.在△ABC中,∠A=35°,∠ B=43 ° 则∠C= .
2.在△ABC中, ∠A :∠B:∠C=2:3:4,则∠A = ∠ B= . ∠ C= .
3.一个三角形中最多有 个直角?为什么?
4.一个三角形中最多有 个钝角?为什么?
5.一个三角形中至少有 个锐角?为什么?
102 °
80 °
60 °
40 °
2
1
1
针对练习
700
800
350
300
700
6.∠C = ( ) , ∠E = ( ) , ∠J = ( ).
30°
115°
20°
针对练习
探索2:三角形的外角与内角有什么关系呢?
思考:三角形的一个外角与相邻的内角有什么关系呢?
∠ACD(外角)+∠ACB(相邻的内角)=180 (互补)
思考:三角形的一个外角与不相邻的两个内角又有什么关系呢?
外角
相邻的内角
不相邻的内角
知识精讲
在一张白纸上画出如图所示的图形,然后把 ∠1、∠2剪下拼在一起,放到∠ 4上,看看会出现什么结果?
发现: ∠1+∠2=∠4
为什么?
知识精讲
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
A
B
C
知识精讲
方法1
2
1
E
D
C
B
A
证明:作CE∥AB,并延长BC到D
∴∠1= ∠A ∠2= ∠B
∴∠1+ ∠2= ∠A+ ∠B
∵ ∠1+ ∠2= ∠ACD,
∴ ∠ACD= ∠A+ ∠B
方法2
知识精讲
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的外角大于任何一个与它不相邻的内角。
∠ACD= ∠ A+ ∠ B
∠ ACD+ ∠ ACB=180°
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
外角+相邻的内角=180
知识精讲
与三角形每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和,如图所示∠1+∠2+∠3就是三角形外角和.
三角形外角和的定义:
(
1
知识精讲
∠1+ =180° ∠2+ =180° ∠3+ =180°
三式相加可以得到
∠1+∠2+∠3+ + + = 。 ①
而 ∠ACB+∠BAC+∠ABC=180° ②
由①②比较得到
∠1+∠2+∠3=360°
(
1
如图所示
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
∠ACB
540°
由此可知,三角形的外角和是
360°
知识精讲
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
解:(1)∵∠ADC是△ABD的外角(已知)
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等于与它不相邻的两个内角之和)
又∵∠B=∠BAD(已知)
∴∠B=80° =40°(等量代换)
典例解析
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
典例解析
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
1.判断
(1)三角形越大,它的内角和就越大。( )
(2) 一个三角形的三个内角度数是:70°、54°、45°。( )
(3)一个三角形中最多只有一个钝角或直角( )
(4) 一个三角形至少有两个锐角( )
(5)三角形的任何一个外角都大于其内角。( )
×
×
×
√
√
达标检测
2.判断∠1与∠3的大小,并说明理由。
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
解:∠3 > ∠1
达标检测
3.已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数.
(三角形内角和定理)
解:设∠A=x,则∠ABC=∠C=2x
∴x+2x+2x= 180°
解得x=36
∴∠C=2×36°=72°
∴∠DBC=180°-90°-72°(三角形内角和定理)
在△BDC中,∵∠BDC=90° (三角形高的定义)
∴∠DBC=18°
达标检测
https://www.21cnjy.com/help/help_extract.php
