9.2 多边形的内角和与外角和(1)课件(共25张PPT)
文档属性
| 名称 | 9.2 多边形的内角和与外角和(1)课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 06:24:14 | ||
图片预览





文档简介
(共25张PPT)
2022年春华师大版数学
七年级下册数学精品课件
多边形的内角和与外角和(1)
学习目标
理解多边形和正多边形的定义.
掌握多边形内角和公式.
会用多边形内角和公式进行相关计算.
请孩子们回忆一下自己截止目前已经学过那些图形?书桌的桌面是什么图形?电子白板面是什么图形?
问题1
问题2
若将长方形的一个角剪掉,会出现什么样的图形?
问题引入
我们已经知道三角形的定义,你能说出什么叫四边形?五边形?
由四条不在同一直线上的线段首尾顺次连结组成的图形叫四边形
由五条不在同一直线上的线段首尾顺次连结组成的图形叫五边形
……
知识精讲
由n条不在同一直线上的线段首尾顺次连结组成的图形叫n边形.
下列图形中,哪些是多边形?
总结
小牛试刀
(1) (2) (3) (4) (5)
√
√
√
知识精讲
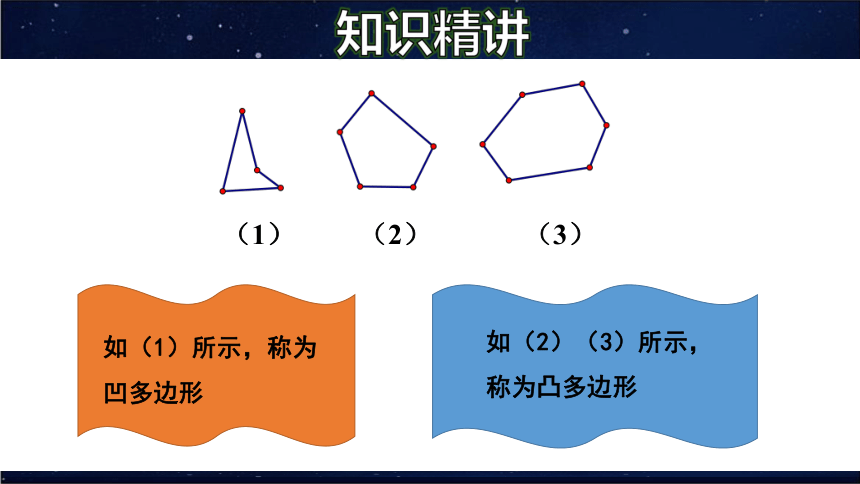
如(1)所示,称为凹多边形
如(2)(3)所示,称为凸多边形
(1) (2) (3)
知识精讲
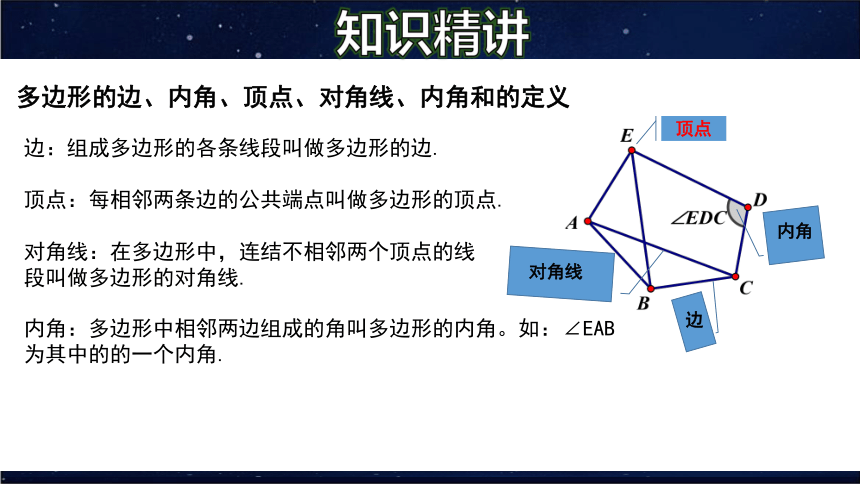
多边形的边、内角、顶点、对角线、内角和的定义
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
对角线:在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线.
内角:多边形中相邻两边组成的角叫多边形的内角。如:∠EAB为其中的的一个内角.
顶点
内角
边
对角线
知识精讲
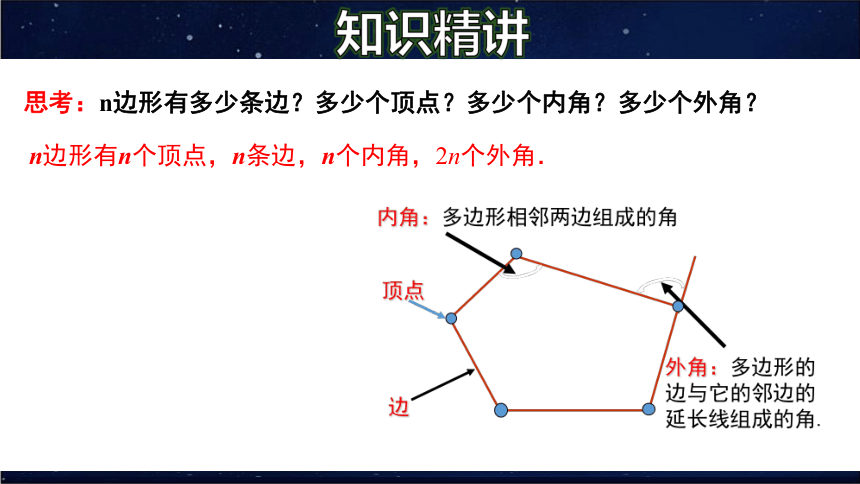
思考:n边形有多少条边?多少个顶点?多少个内角?多少个外角?
知识精讲
n边形有n个顶点,n条边,n个内角,2n个外角.
问题3
观察下列各图,均有什么特征?你发现了什么?
正三角形 正四边形 正五边形 正六边形
小结
各边都相等,各内角也都相等的多边形,称为正多边形.
知识精讲
问题4
从n边形的一个顶点出发可以引出多少条对角线?这些对角线可以将这个n边形分成多少个三角形?利用三角形内角和知识,我们可以猜想:n边形内角和是多少呢?
知识精讲
多边形的边数 4 5 6 7 … n
从一个顶点引出的对角线的条数 1 2 3 4 …
对角线的总条数 2 5 9 …
探究:从n边形的一个顶点出发可以引出多少条对角线?
n-3
14
知识精讲
多边形的边数 3 4 5 6 7 … n
分成的三角形的个数 1 2 …
多边形的内角和 180° 360° …
根据教材p84页图9.2.4所示,填写p85页表9.2.1,探究多边形的内角和是多少?
3
4
5
n-2
540°
720°
900°
知识精讲
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
多边形的内角和为(n-2) 180°.
知识精讲
解:八边形的内角和为
(n-2) 180°=(8-2) 180°=1080°.
例1:求八边形内角和.
典例解析
例2:已知一个多边形的内角和等于2160°,求这个多边形的边数?
解 设这个多边形的边数为n,根据题意,得
(n-2) 180°=2160°
解得 n=14
即这个多边形的边数为14
典例解析
1.下列多边形中,不是凸多边形的是( )
A
B
C
D
B
2.把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 六边形 B . 五边形 C.四边形 D.三角形
A
达标检测
3.九边形的对角线有( )
A.25条 B.31条 C.27条 D.30条
C
4.若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是 边形.
十三
5.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
六
达标检测
(1)做多边形所有过顶点A的对角线,并分别用字母表示出来
(2)求这个多边形的内角和
6.如下图
达标检测
解:(1)如图所示
(2)由图可知,此多边形为五边形因此利用多边形的内角和公式可得
(n-2) 180°=(5-2) 180°=540°
达标检测
7.如图9.2.5在n边形(图中取n=6的情形)内任意一点p,连结点p与多边形的每一个顶点,可得到几个三角形?你能否利用这样划分多边形的方法来说明n边形的内角和呢?
达标检测
探究:如下图所示,探究多边形内角和,完成下表
探究:如下图所示,探究多边形内角和,完成下表
多边形的边数 3 4 5 6 7 … n
分成的三角形的个数 3 4 5 6 7 … n
三角形内角和
多边形的内角和
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
多边形的内角和与外角和(1)
学习目标
理解多边形和正多边形的定义.
掌握多边形内角和公式.
会用多边形内角和公式进行相关计算.
请孩子们回忆一下自己截止目前已经学过那些图形?书桌的桌面是什么图形?电子白板面是什么图形?
问题1
问题2
若将长方形的一个角剪掉,会出现什么样的图形?
问题引入
我们已经知道三角形的定义,你能说出什么叫四边形?五边形?
由四条不在同一直线上的线段首尾顺次连结组成的图形叫四边形
由五条不在同一直线上的线段首尾顺次连结组成的图形叫五边形
……
知识精讲
由n条不在同一直线上的线段首尾顺次连结组成的图形叫n边形.
下列图形中,哪些是多边形?
总结
小牛试刀
(1) (2) (3) (4) (5)
√
√
√
知识精讲
如(1)所示,称为凹多边形
如(2)(3)所示,称为凸多边形
(1) (2) (3)
知识精讲
多边形的边、内角、顶点、对角线、内角和的定义
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
对角线:在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线.
内角:多边形中相邻两边组成的角叫多边形的内角。如:∠EAB为其中的的一个内角.
顶点
内角
边
对角线
知识精讲
思考:n边形有多少条边?多少个顶点?多少个内角?多少个外角?
知识精讲
n边形有n个顶点,n条边,n个内角,2n个外角.
问题3
观察下列各图,均有什么特征?你发现了什么?
正三角形 正四边形 正五边形 正六边形
小结
各边都相等,各内角也都相等的多边形,称为正多边形.
知识精讲
问题4
从n边形的一个顶点出发可以引出多少条对角线?这些对角线可以将这个n边形分成多少个三角形?利用三角形内角和知识,我们可以猜想:n边形内角和是多少呢?
知识精讲
多边形的边数 4 5 6 7 … n
从一个顶点引出的对角线的条数 1 2 3 4 …
对角线的总条数 2 5 9 …
探究:从n边形的一个顶点出发可以引出多少条对角线?
n-3
14
知识精讲
多边形的边数 3 4 5 6 7 … n
分成的三角形的个数 1 2 …
多边形的内角和 180° 360° …
根据教材p84页图9.2.4所示,填写p85页表9.2.1,探究多边形的内角和是多少?
3
4
5
n-2
540°
720°
900°
知识精讲
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
多边形的内角和为(n-2) 180°.
知识精讲
解:八边形的内角和为
(n-2) 180°=(8-2) 180°=1080°.
例1:求八边形内角和.
典例解析
例2:已知一个多边形的内角和等于2160°,求这个多边形的边数?
解 设这个多边形的边数为n,根据题意,得
(n-2) 180°=2160°
解得 n=14
即这个多边形的边数为14
典例解析
1.下列多边形中,不是凸多边形的是( )
A
B
C
D
B
2.把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 六边形 B . 五边形 C.四边形 D.三角形
A
达标检测
3.九边形的对角线有( )
A.25条 B.31条 C.27条 D.30条
C
4.若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是 边形.
十三
5.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
六
达标检测
(1)做多边形所有过顶点A的对角线,并分别用字母表示出来
(2)求这个多边形的内角和
6.如下图
达标检测
解:(1)如图所示
(2)由图可知,此多边形为五边形因此利用多边形的内角和公式可得
(n-2) 180°=(5-2) 180°=540°
达标检测
7.如图9.2.5在n边形(图中取n=6的情形)内任意一点p,连结点p与多边形的每一个顶点,可得到几个三角形?你能否利用这样划分多边形的方法来说明n边形的内角和呢?
达标检测
探究:如下图所示,探究多边形内角和,完成下表
探究:如下图所示,探究多边形内角和,完成下表
多边形的边数 3 4 5 6 7 … n
分成的三角形的个数 3 4 5 6 7 … n
三角形内角和
多边形的内角和
达标检测
https://www.21cnjy.com/help/help_extract.php
