9.3 用正多边形铺设地面(1)课件(共20张PPT)
文档属性
| 名称 | 9.3 用正多边形铺设地面(1)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 06:52:23 | ||
图片预览







文档简介
(共20张PPT)
2022年春华师大版数学
七年级下册数学精品课件
学习目标
通过用相同的正多边形拼地板的活动,巩固多边形的内角和与外角和公式.
通过“拼地板”和相关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是几个多边形的内角和相加要等于360°.
问题1
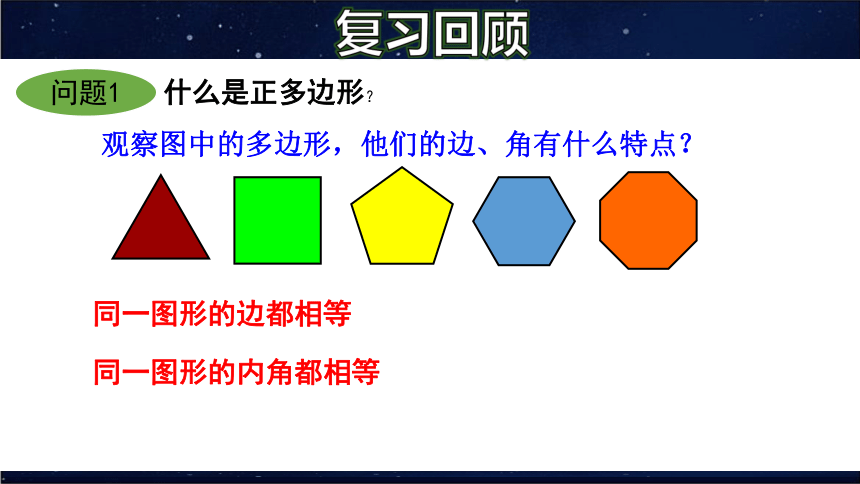
什么是正多边形?
观察图中的多边形,他们的边、角有什么特点?
同一图形的边都相等
同一图形的内角都相等
复习回顾
正多边形的定义:
各边都相等,各内角也都相等的多边形叫做正多边形.
如图中的多边形分别为:正三角形、正四边形(即正方形)、正五边形、正六边形、正八边形.
复习回顾
问题2
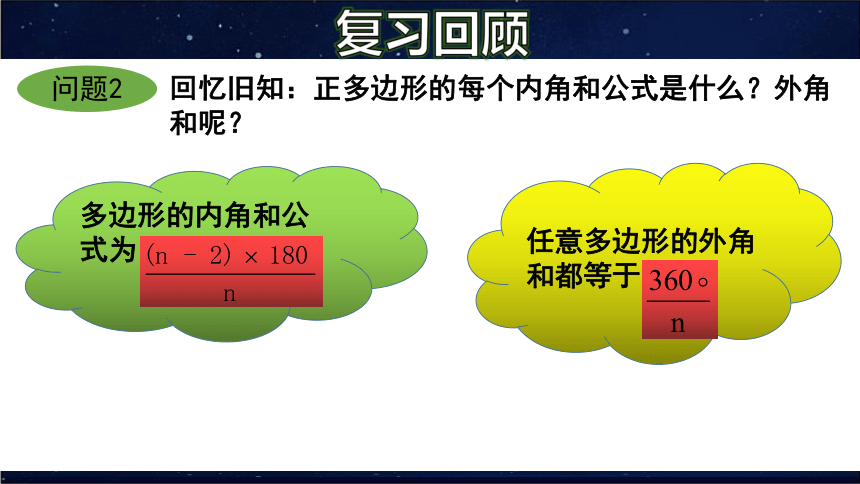
回忆旧知:正多边形的每个内角和公式是什么?外角和呢?
任意多边形的外角和都等于
多边形的内角和公式为
复习回顾
1.用相同的正多边形如何密铺?
观察这些美丽的图案,你有什么发现?
知识精讲
60°
60°
60°
60°
60°
60°
正三角形瓷砖
围绕每一点有6个角,6个角和为6×60°= 360°
知识精讲
90°
90°
90°
90°
正方形瓷砖
围绕每一点有4个角,4个角和为4×90°=360°
知识精讲
108°
108°
108°
正五边形瓷砖
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
知识精讲
120°
120°
120°
正六边形瓷砖
围绕每一点有3个角,3个角和为3×120°=360°
知识精讲
正七边形正八边形呢?
想一想,为什么?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7≈128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
知识精讲
思考:
为什么有的正多边形能铺满地面,有的却不行呢?
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
知识精讲
n只能是哪些数?
总结:
能用同一种正多边形拼地板的正多边形只有正三角形、正方形、正六边形.
探究:
正多边形的边数 能否铺满整个地面
3
4
5
6
7
8
…
√
√
√
知识精讲
1.下列多边形中,能够铺满地面的是( )(多选)
A 正方形 B 正五边形 C 正八边形 D 正六边形
2.用形状、大小完全形相同的图形不能镶嵌成平面图形的是( )
A 正三角形 B 正四边形 C正七边形 D 正六边形
ACD
C
达标检测
相同的正多边形可以铺满整个地面,有没有不同的正多边形铺满整个地面呢?
达标检测
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
小结梳理
能用同一种正多边形拼地板的正多边形只有正三角形、正
方形、正六边形.
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
学习目标
通过用相同的正多边形拼地板的活动,巩固多边形的内角和与外角和公式.
通过“拼地板”和相关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是几个多边形的内角和相加要等于360°.
问题1
什么是正多边形?
观察图中的多边形,他们的边、角有什么特点?
同一图形的边都相等
同一图形的内角都相等
复习回顾
正多边形的定义:
各边都相等,各内角也都相等的多边形叫做正多边形.
如图中的多边形分别为:正三角形、正四边形(即正方形)、正五边形、正六边形、正八边形.
复习回顾
问题2
回忆旧知:正多边形的每个内角和公式是什么?外角和呢?
任意多边形的外角和都等于
多边形的内角和公式为
复习回顾
1.用相同的正多边形如何密铺?
观察这些美丽的图案,你有什么发现?
知识精讲
60°
60°
60°
60°
60°
60°
正三角形瓷砖
围绕每一点有6个角,6个角和为6×60°= 360°
知识精讲
90°
90°
90°
90°
正方形瓷砖
围绕每一点有4个角,4个角和为4×90°=360°
知识精讲
108°
108°
108°
正五边形瓷砖
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
知识精讲
120°
120°
120°
正六边形瓷砖
围绕每一点有3个角,3个角和为3×120°=360°
知识精讲
正七边形正八边形呢?
想一想,为什么?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7≈128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
知识精讲
思考:
为什么有的正多边形能铺满地面,有的却不行呢?
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
知识精讲
n只能是哪些数?
总结:
能用同一种正多边形拼地板的正多边形只有正三角形、正方形、正六边形.
探究:
正多边形的边数 能否铺满整个地面
3
4
5
6
7
8
…
√
√
√
知识精讲
1.下列多边形中,能够铺满地面的是( )(多选)
A 正方形 B 正五边形 C 正八边形 D 正六边形
2.用形状、大小完全形相同的图形不能镶嵌成平面图形的是( )
A 正三角形 B 正四边形 C正七边形 D 正六边形
ACD
C
达标检测
相同的正多边形可以铺满整个地面,有没有不同的正多边形铺满整个地面呢?
达标检测
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
小结梳理
能用同一种正多边形拼地板的正多边形只有正三角形、正
方形、正六边形.
https://www.21cnjy.com/help/help_extract.php
