6.1 平方根(第1课时)课件(共37张PPT)
文档属性
| 名称 | 6.1 平方根(第1课时)课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 06:48:08 | ||
图片预览










文档简介
(共37张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第六章 实数
6.1 平方根
第1课时 算术平方根
1.了解算术平方根的概念,会表示正数的算术平方根,并了解算术平方根的非负性.
2.会求一些数的算术平方根,并用算术平方根符号表示.
3.了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根.
学习目标
学校要举行美术作品比赛,小强很
高兴,他想裁出一块面积为25dm2 的正
方形画布,画上自己的得意之作参加比
赛,这块正方形画布的边长应取多少?
因为52 =25,
新知一 算术平方根的概念
所以这块正方形画布的边长应取5dm.
合作探究
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长/cm 1 2 0.5
正方形的面积/cm2
1
填表:
表1
【讨论】你能从表1发现什么共同点吗?
4
0. 25
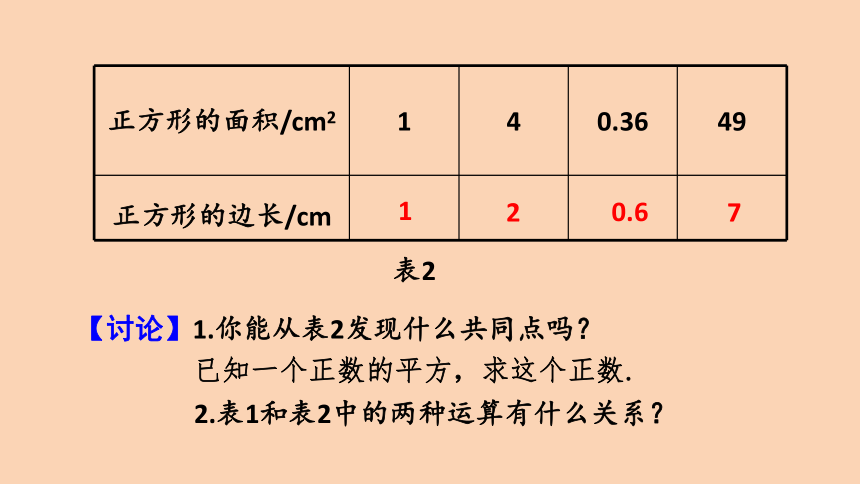
正方形的面积/cm2 1 4 0.36
49
正方形的边长/cm
已知一个正数的平方,求这个正数.
表2
2.表1和表2中的两种运算有什么关系?
1
2
0.6
7
【讨论】1.你能从表2发现什么共同点吗?
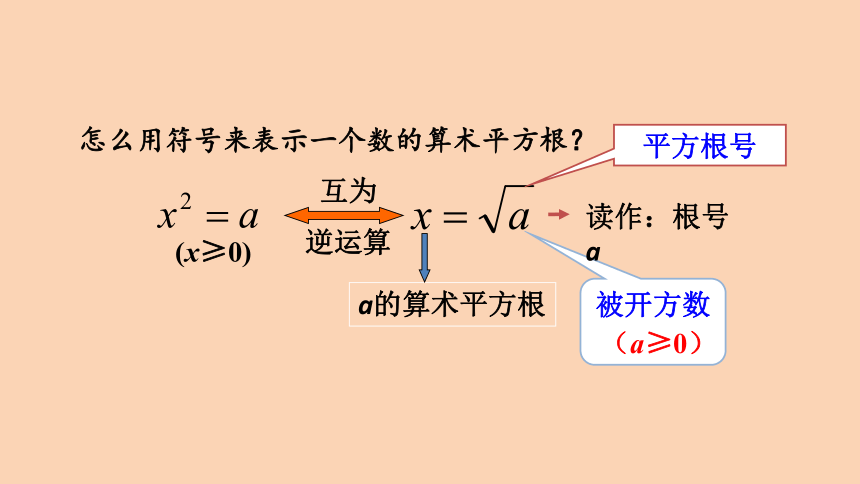
一般地,如果一个正数 x 的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根. a的算术平方根记为 ,读作“ 根号 a” .
规定:0的算术平方根是0,即
.
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
1.一个正数的算术平方根有几个?
0的算术平方根有1个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个.
例 求下列各数的算术平方根:
(1)100 ; (2) ; (3)0.0001.
解:(1)因为 102=100 ,
所以100的算术平方根是10 .
即 .
典例精析 求一个数的算术平方根
解:(2)因为 ,
所以 的算术平方根是 .
即 .
(2) ;
解:(3)因为0.012=0.0001,
所以0.0001的算术平方根是0.01 .
即 .
总结:从例题可以看出:被开方数越大,对应的算术平方根也越大,这个结论对所有正数都成立.
(3)0.0001.
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
解:(1) ;
(2) ;
(3) ;
(4) .
巩固新知
1. 负数有算术平方根吗?
2. 是什么数?
3. 中的a可以取任何数吗?
也就是说,非负数的“算术”平方根是非负数.负数不存在算术平方根,即当 a<0 时, 无意义.
新知二 算术平方根的双重非负性
的双重非负性
1.被开方数a≥0
2.a的算术平方根
合作探究
例1 下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:
(1)无意义;
(4)有意义.
(3)有意义;
(2)有意义;
典例精析1 算术平方根有意义的识别
1.下列各式是否有意义,为什么?
2.下列各式中,x为何值时有意义?
∵-x≥0
∴x≤0
∵x2+1≥0恒成立
∴x为任何数
×
√
√
√
(1)
(2)
(1)
(2)
(3)
(4)
解:
解:
巩固新知
解: 因为|m-1| ≥0, ≥0,又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
例2 若|m-1| + =0,求m+n的值.
总结:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
典例精析2 利用非负性求字母的值
合作探究
(3)若 ,则a= ;
(2)若 (m-7)2=0 ,则m= ;
(4)若 ,则代数式 =___.
(1)若|a+3|=0 , 则a= ;
-3
7
5
-1
求下列各式中字母的值.
巩固新知
1.(3分)(株洲中考)9的算术平方根是( )
A.3 B.9 C.±3 D.±9
2.(3分)下列各数没有算术平方根的是( )
A.0 B.(-2)2
C.-32 D.6
A
C
课堂练习
B
4.(3分)下列说法正确的是( )
A.5是25的算术平方根
B.±4是16的算术平方根
C.-6是(-6)2的算术平方根
D.0.01是0.1的算术平方根
A
B
40
B
C
7
算术平方根
算术平方根的概念
算术平方根的双重非负性
算术平方根的应用
归纳新知
B
C
课后练习
A
1或0
0.2284
228.4
0.0005217
解:原式=5-4+2=3
解:原式=0.01×100+6×0.2=1+1.2=2.2
10.如图,公园里有一块面积为400平方米的正方形空地,园林设计师计划按图中方法在此空地上建一个面积为300平方米的长方形花坛,使长方形的长宽之比为5:3.
(1)求计划设计的花坛的长和宽;
(2)请你通过计算说明设计师能否实现这个计划.
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第六章 实数
6.1 平方根
第1课时 算术平方根
1.了解算术平方根的概念,会表示正数的算术平方根,并了解算术平方根的非负性.
2.会求一些数的算术平方根,并用算术平方根符号表示.
3.了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根.
学习目标
学校要举行美术作品比赛,小强很
高兴,他想裁出一块面积为25dm2 的正
方形画布,画上自己的得意之作参加比
赛,这块正方形画布的边长应取多少?
因为52 =25,
新知一 算术平方根的概念
所以这块正方形画布的边长应取5dm.
合作探究
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长/cm 1 2 0.5
正方形的面积/cm2
1
填表:
表1
【讨论】你能从表1发现什么共同点吗?
4
0. 25
正方形的面积/cm2 1 4 0.36
49
正方形的边长/cm
已知一个正数的平方,求这个正数.
表2
2.表1和表2中的两种运算有什么关系?
1
2
0.6
7
【讨论】1.你能从表2发现什么共同点吗?
一般地,如果一个正数 x 的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根. a的算术平方根记为 ,读作“ 根号 a” .
规定:0的算术平方根是0,即
.
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
1.一个正数的算术平方根有几个?
0的算术平方根有1个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个.
例 求下列各数的算术平方根:
(1)100 ; (2) ; (3)0.0001.
解:(1)因为 102=100 ,
所以100的算术平方根是10 .
即 .
典例精析 求一个数的算术平方根
解:(2)因为 ,
所以 的算术平方根是 .
即 .
(2) ;
解:(3)因为0.012=0.0001,
所以0.0001的算术平方根是0.01 .
即 .
总结:从例题可以看出:被开方数越大,对应的算术平方根也越大,这个结论对所有正数都成立.
(3)0.0001.
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
解:(1) ;
(2) ;
(3) ;
(4) .
巩固新知
1. 负数有算术平方根吗?
2. 是什么数?
3. 中的a可以取任何数吗?
也就是说,非负数的“算术”平方根是非负数.负数不存在算术平方根,即当 a<0 时, 无意义.
新知二 算术平方根的双重非负性
的双重非负性
1.被开方数a≥0
2.a的算术平方根
合作探究
例1 下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:
(1)无意义;
(4)有意义.
(3)有意义;
(2)有意义;
典例精析1 算术平方根有意义的识别
1.下列各式是否有意义,为什么?
2.下列各式中,x为何值时有意义?
∵-x≥0
∴x≤0
∵x2+1≥0恒成立
∴x为任何数
×
√
√
√
(1)
(2)
(1)
(2)
(3)
(4)
解:
解:
巩固新知
解: 因为|m-1| ≥0, ≥0,又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
例2 若|m-1| + =0,求m+n的值.
总结:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
典例精析2 利用非负性求字母的值
合作探究
(3)若 ,则a= ;
(2)若 (m-7)2=0 ,则m= ;
(4)若 ,则代数式 =___.
(1)若|a+3|=0 , 则a= ;
-3
7
5
-1
求下列各式中字母的值.
巩固新知
1.(3分)(株洲中考)9的算术平方根是( )
A.3 B.9 C.±3 D.±9
2.(3分)下列各数没有算术平方根的是( )
A.0 B.(-2)2
C.-32 D.6
A
C
课堂练习
B
4.(3分)下列说法正确的是( )
A.5是25的算术平方根
B.±4是16的算术平方根
C.-6是(-6)2的算术平方根
D.0.01是0.1的算术平方根
A
B
40
B
C
7
算术平方根
算术平方根的概念
算术平方根的双重非负性
算术平方根的应用
归纳新知
B
C
课后练习
A
1或0
0.2284
228.4
0.0005217
解:原式=5-4+2=3
解:原式=0.01×100+6×0.2=1+1.2=2.2
10.如图,公园里有一块面积为400平方米的正方形空地,园林设计师计划按图中方法在此空地上建一个面积为300平方米的长方形花坛,使长方形的长宽之比为5:3.
(1)求计划设计的花坛的长和宽;
(2)请你通过计算说明设计师能否实现这个计划.
https://www.21cnjy.com/help/help_extract.php
