苏教版八年级物理下册6.4密度知识的应用 课件(共27张PPT)
文档属性
| 名称 | 苏教版八年级物理下册6.4密度知识的应用 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-04 08:26:31 | ||
图片预览







文档简介
(共27张PPT)
第六章 第四节
密度知识的应用
苏科版 物理
八年级 第二学期
3.量筒上的标度
单位: 毫升 mL
1 mL = 1 cm3
最大测量值:常用100 mL,200 mL
分度: 1 mL, 2 mL,5 mL
1.量筒是测量液体体积的仪器;
2.观察量筒,思考问题。
(1)量筒的最大测量值
(2)量筒的分度值
一、量筒(量杯)的使用
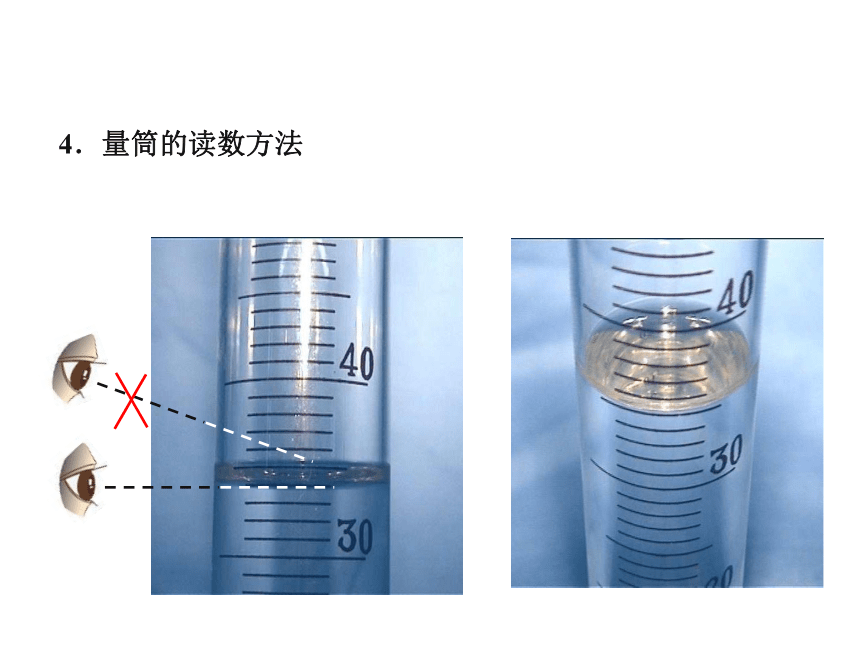
4.量筒的读数方法
认识量筒和量杯
用量筒测液体的积。量筒里的水面是凹形的,读数时,应把量筒放在水平桌面上,观察刻度时,视线、刻度线与量筒内液体的凹液面最低处三者保持水平。
量筒的使用方法
在看量筒的容积时是看液面的中心点
俯视时视线斜向下 视线与筒壁的交点在液面上所以读到的数据偏高,实际值偏低。即俯视液面,读数偏大。
仰视时视线斜向上 视线与筒壁的交点在液面下所以读到的数据偏低,实际值偏高。即仰视液面,读数偏小。
例 向量筒内注入水,俯视读数为20mL,倒出一部分后,仰视读数为12mL,则倒出的水的体积为( )
A. 等于8mL B. 大于8mL
C. 小于8mL D. 无法确定
解析:读数时俯视刻度,读出的数值比实际数值大;读数时仰视刻度,读出的数值比实际数值小。本题中,第一次读数是俯视,量筒内水的实际体积小于20mL;第二次读数是仰视,量筒内剩余的水的实际体积大于12mL;故倒出的水的体积小于8mL。选C。
C
用量筒可以直接测出液体的体积。
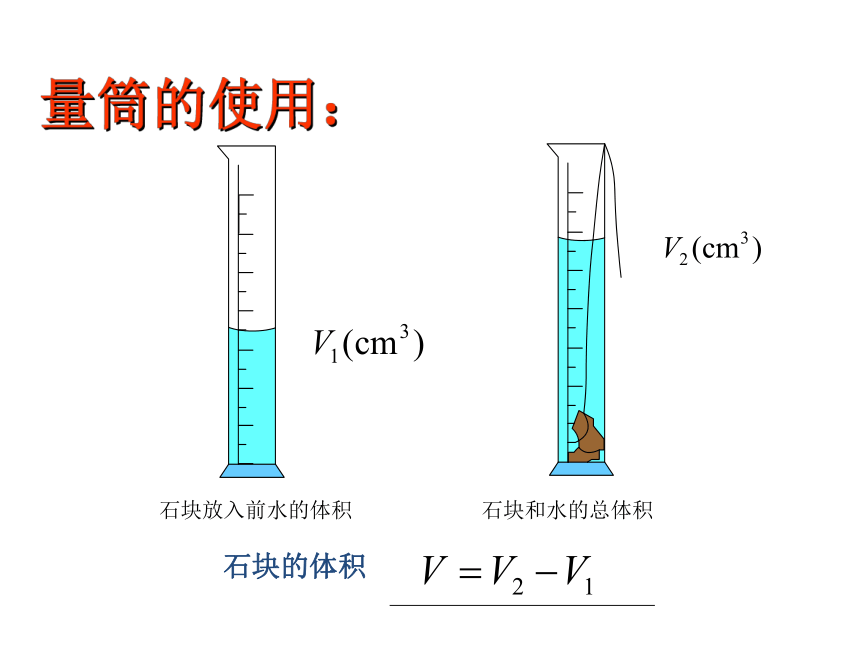
对于形状不规则的固体,因用刻度尺根本无法测出其体积。这时只能用量筒利用排水法进行测量。具体方法是:先在量筒中倒入适量的水,读出水面所对刻度V1,再将被测物体轻放入或按入水中,读出此时读数V2,V2﹣V1即是该固体的体积。
石块的体积
石块放入前水的体积
石块和水的总体积
测量密度的实验原理及实验器材
1.实验原理
2.测量仪器:
天平、量筒
3.测量对象:
盐水
石块
二、测量物质的密度
1.实验原理:
3.实验步骤:
2.实验器材:
石块 细绳 天平和砝码 烧杯 水 量筒
1.用天平称出石块的质量。
2.用量筒测出石块的体积。
(一)测量固体的密度(可以沉入水中的物体)
m
V
ρ=
4.实验操作
“小石块”
m
V1
V2
5.实验结果:
ρ=
V2﹣V1
m
6.(1)设计表格
石块的质量
石块放入前水的体积 石块和水的总体积 石块的体积
石块的密度
(2)将实验数据记在表中,求出石块的密度。
)
cm
(
3
V
量筒里的水面是凹形的,读数时,视线要跟凹面相平。
7.注意量筒的读数应该
蜡块不沉入水中,也能用天平和量筒测出蜡块的密度吗?想想看,有什么好办法?
?
(1)针压法
(二)测量固体的密度(不可以沉入水中的物体)
4)读出水和木块的总体积V2
1)用天平测量木块的质量m
木块的密度
3)用针将木块压入水中
2)读出量筒中水的体积V1
m
V2﹣V1
ρ=
(2)悬垂法
4)水和悬垂物和木块的体积)V2
1)用天平测量木块的质量m
木块的密度
2)水和悬垂物的体积V1
3)用悬垂物将木块悬入水中
m
V2﹣V1
ρ=
1.实验原理:
2.实验器材:
天平和砝码 量筒 烧杯 待测液体
(三)测量液体的密度
m
V2﹣V1
ρ=
3.(1)设计表格
(2)将实验数据记在表中,求出液体的密度。
玻璃杯和水的质量m1(g) 玻璃杯和剩余水的质量m2(g) 量筒中水质量m=m1﹣m2(g) 量筒中水的体积 V(cm3) 水的密度 ρ(g/cm3)
测量液体的正确方法(步骤)
用天平测杯和液体的总质量
m1
液体密度
倒到量筒中一部分读出液体的体积V
用天平测量剩余液体和杯的总质量m2
m1﹣m2
V
ρ=
其它方法(1)
将杯中装一定量某液体,用天平测总质量m2
用天平测空杯质量m1
1)液体密度
2)测量结果偏大(因为体积偏小)
将杯中该液体全部倒到量筒中,读量筒内液体的体积V
m2﹣m1
V
ρ=
其它方法(2)
用天平测量杯和液体质量m1
1)液体密度
2)测量结果偏小(因为质量偏小)
读量杯内液体的体积V
将液体全部倒出用天平测量空量杯质量m1
m1﹣m2
V
ρ=
1)没有量筒,只有天平和水,烧杯及待测液体,请写实验步骤和结论
2)有天平但没有砝码,水、烧杯、刻度尺及待测液体,请写实验步骤和结论
3)有天平、水,烧杯及待测固体,请写实验步骤和结论
1.计算物质的密度: ρ=m / V
计算密度、鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子等一些形状不规则的物体)
3.计算物体的质量: m=ρV
有些物体的质量太大不便于直接测量
三、密度公式的应用
1.计算物质的密度: ρ=m/V
例 某届亚运会纪念币,它的质量为16 .1g,体积为1 .8dm3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
例 用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103
千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子等一些形状不规则的物体)
解:由公式ρ=m/V得
V= m/ρ=445g/8.9g/cm3= 50cm3
注:如果知道铜丝的横截面积还可以计算出这捆铜丝的长度。
3.计算物体的质量: m=ρV
例 矗立在天安门广场的人民英雄纪念碑,它的碑心石是一块巨大的花岗岩,在长14.7m,宽2.9m,厚1m的碑心石上刻着“人民英雄永垂不朽”。怎样知道它的质量?
解:V=14.7m×2.9m×1m= 42.6m3
由公式ρ=m/V得
m=ρV= 2.6×103kg/m3 ×42.6m3= 110.76×103kg
答:碑心石的质量是110.76×103kg。
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
练习 一个铝球,它的体积是500cm3,质量是540g,问是否是实心的?(已知ρ铝= 2.7g/cm3)
比较质量法:假定铝球是实心的,计算铝球质量是1350g,因为1350g>540g ,判定该铝球是空心的。
比较体积法:质量是540g的实心铝球计算体积应是200cm3,因为200cm3<500cm3,判定该铝球是空心的。
比较密度法:用质量比体积可以得到该球的平均密度是1.08g/cm3,因为1.08kg/cm3<2.7g/cm3,判定该铝球是空心的。
第六章 第四节
密度知识的应用
苏科版 物理
八年级 第二学期
3.量筒上的标度
单位: 毫升 mL
1 mL = 1 cm3
最大测量值:常用100 mL,200 mL
分度: 1 mL, 2 mL,5 mL
1.量筒是测量液体体积的仪器;
2.观察量筒,思考问题。
(1)量筒的最大测量值
(2)量筒的分度值
一、量筒(量杯)的使用
4.量筒的读数方法
认识量筒和量杯
用量筒测液体的积。量筒里的水面是凹形的,读数时,应把量筒放在水平桌面上,观察刻度时,视线、刻度线与量筒内液体的凹液面最低处三者保持水平。
量筒的使用方法
在看量筒的容积时是看液面的中心点
俯视时视线斜向下 视线与筒壁的交点在液面上所以读到的数据偏高,实际值偏低。即俯视液面,读数偏大。
仰视时视线斜向上 视线与筒壁的交点在液面下所以读到的数据偏低,实际值偏高。即仰视液面,读数偏小。
例 向量筒内注入水,俯视读数为20mL,倒出一部分后,仰视读数为12mL,则倒出的水的体积为( )
A. 等于8mL B. 大于8mL
C. 小于8mL D. 无法确定
解析:读数时俯视刻度,读出的数值比实际数值大;读数时仰视刻度,读出的数值比实际数值小。本题中,第一次读数是俯视,量筒内水的实际体积小于20mL;第二次读数是仰视,量筒内剩余的水的实际体积大于12mL;故倒出的水的体积小于8mL。选C。
C
用量筒可以直接测出液体的体积。
对于形状不规则的固体,因用刻度尺根本无法测出其体积。这时只能用量筒利用排水法进行测量。具体方法是:先在量筒中倒入适量的水,读出水面所对刻度V1,再将被测物体轻放入或按入水中,读出此时读数V2,V2﹣V1即是该固体的体积。
石块的体积
石块放入前水的体积
石块和水的总体积
测量密度的实验原理及实验器材
1.实验原理
2.测量仪器:
天平、量筒
3.测量对象:
盐水
石块
二、测量物质的密度
1.实验原理:
3.实验步骤:
2.实验器材:
石块 细绳 天平和砝码 烧杯 水 量筒
1.用天平称出石块的质量。
2.用量筒测出石块的体积。
(一)测量固体的密度(可以沉入水中的物体)
m
V
ρ=
4.实验操作
“小石块”
m
V1
V2
5.实验结果:
ρ=
V2﹣V1
m
6.(1)设计表格
石块的质量
石块放入前水的体积 石块和水的总体积 石块的体积
石块的密度
(2)将实验数据记在表中,求出石块的密度。
)
cm
(
3
V
量筒里的水面是凹形的,读数时,视线要跟凹面相平。
7.注意量筒的读数应该
蜡块不沉入水中,也能用天平和量筒测出蜡块的密度吗?想想看,有什么好办法?
?
(1)针压法
(二)测量固体的密度(不可以沉入水中的物体)
4)读出水和木块的总体积V2
1)用天平测量木块的质量m
木块的密度
3)用针将木块压入水中
2)读出量筒中水的体积V1
m
V2﹣V1
ρ=
(2)悬垂法
4)水和悬垂物和木块的体积)V2
1)用天平测量木块的质量m
木块的密度
2)水和悬垂物的体积V1
3)用悬垂物将木块悬入水中
m
V2﹣V1
ρ=
1.实验原理:
2.实验器材:
天平和砝码 量筒 烧杯 待测液体
(三)测量液体的密度
m
V2﹣V1
ρ=
3.(1)设计表格
(2)将实验数据记在表中,求出液体的密度。
玻璃杯和水的质量m1(g) 玻璃杯和剩余水的质量m2(g) 量筒中水质量m=m1﹣m2(g) 量筒中水的体积 V(cm3) 水的密度 ρ(g/cm3)
测量液体的正确方法(步骤)
用天平测杯和液体的总质量
m1
液体密度
倒到量筒中一部分读出液体的体积V
用天平测量剩余液体和杯的总质量m2
m1﹣m2
V
ρ=
其它方法(1)
将杯中装一定量某液体,用天平测总质量m2
用天平测空杯质量m1
1)液体密度
2)测量结果偏大(因为体积偏小)
将杯中该液体全部倒到量筒中,读量筒内液体的体积V
m2﹣m1
V
ρ=
其它方法(2)
用天平测量杯和液体质量m1
1)液体密度
2)测量结果偏小(因为质量偏小)
读量杯内液体的体积V
将液体全部倒出用天平测量空量杯质量m1
m1﹣m2
V
ρ=
1)没有量筒,只有天平和水,烧杯及待测液体,请写实验步骤和结论
2)有天平但没有砝码,水、烧杯、刻度尺及待测液体,请写实验步骤和结论
3)有天平、水,烧杯及待测固体,请写实验步骤和结论
1.计算物质的密度: ρ=m / V
计算密度、鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子等一些形状不规则的物体)
3.计算物体的质量: m=ρV
有些物体的质量太大不便于直接测量
三、密度公式的应用
1.计算物质的密度: ρ=m/V
例 某届亚运会纪念币,它的质量为16 .1g,体积为1 .8dm3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
例 用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103
千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子等一些形状不规则的物体)
解:由公式ρ=m/V得
V= m/ρ=445g/8.9g/cm3= 50cm3
注:如果知道铜丝的横截面积还可以计算出这捆铜丝的长度。
3.计算物体的质量: m=ρV
例 矗立在天安门广场的人民英雄纪念碑,它的碑心石是一块巨大的花岗岩,在长14.7m,宽2.9m,厚1m的碑心石上刻着“人民英雄永垂不朽”。怎样知道它的质量?
解:V=14.7m×2.9m×1m= 42.6m3
由公式ρ=m/V得
m=ρV= 2.6×103kg/m3 ×42.6m3= 110.76×103kg
答:碑心石的质量是110.76×103kg。
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
练习 一个铝球,它的体积是500cm3,质量是540g,问是否是实心的?(已知ρ铝= 2.7g/cm3)
比较质量法:假定铝球是实心的,计算铝球质量是1350g,因为1350g>540g ,判定该铝球是空心的。
比较体积法:质量是540g的实心铝球计算体积应是200cm3,因为200cm3<500cm3,判定该铝球是空心的。
比较密度法:用质量比体积可以得到该球的平均密度是1.08g/cm3,因为1.08kg/cm3<2.7g/cm3,判定该铝球是空心的。
