苏科版七年级数学下册 10.3 解二元一次方程组 课件(共15张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 10.3 解二元一次方程组 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 15:01:17 | ||
图片预览





文档简介
(共15张PPT)
10.3 解二元一次方程组
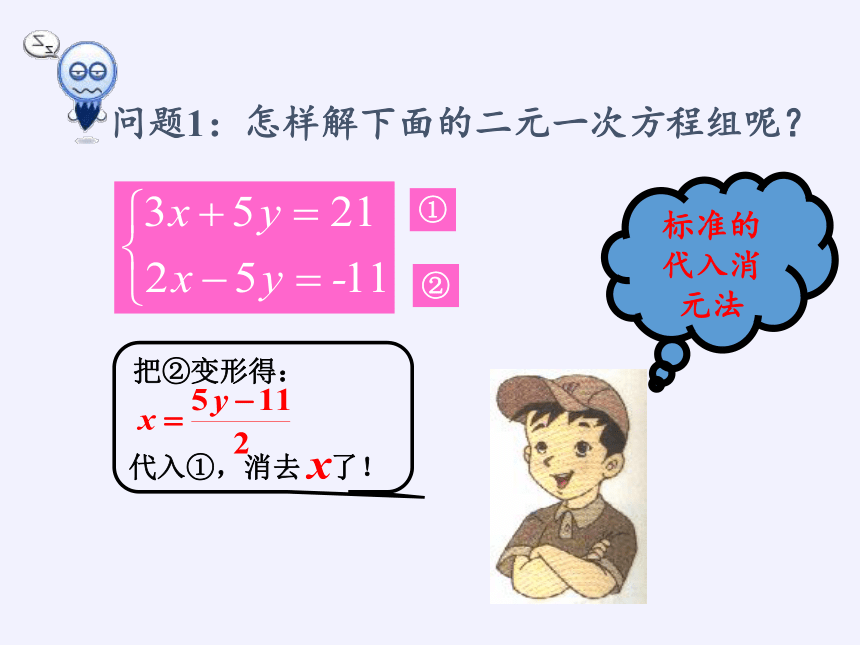
问题1:怎样解下面的二元一次方程组呢?
①
②
代入①,消去 了!
把②变形得:
标准的代入消元法
问题2:还有其他办法求解吗?
①
②
简便的代入消元法
把②变形得
可以直接代入①呀!
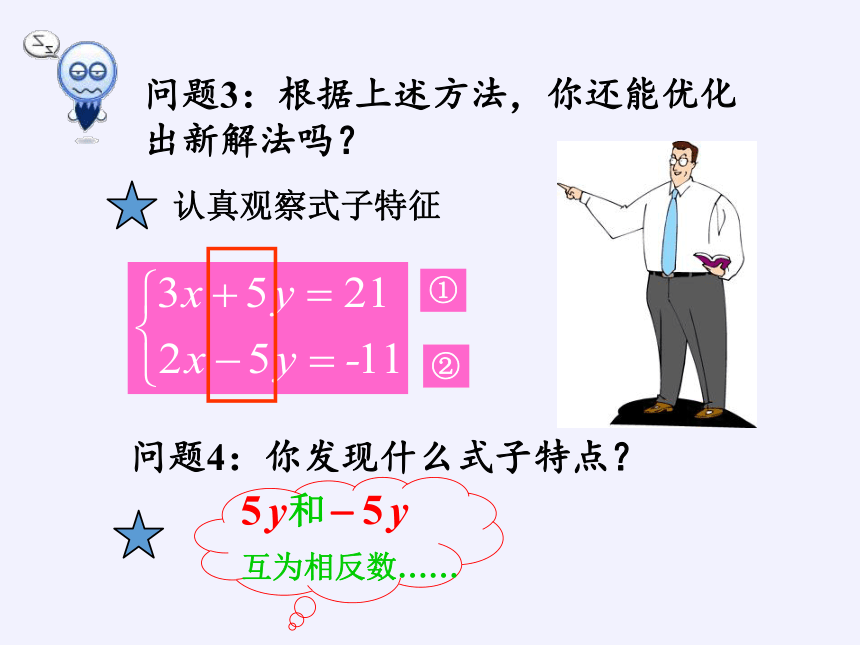
问题3:根据上述方法,你还能优化出新解法吗?
①
②
认真观察式子特征
问题4:你发现什么式子特点?
和
互为相反数……
①
②
3x+5y +2x - 5y =10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
(3x + 5y)+(2x - 5y)= 21 + (-11)
等式性质
问题5:你有何策略消去未知数y吗?
问题6:新思路,新体验,你有什么感想?
整体相加
式子简化
思想:转化划归思想
特点:灵活巧妙
依据:等式的性质1
前提:观察式子结构
①
②
问题7:类比学习,你对下面的方程组的解法有什么新的见解?
学会知识迁移是一件了不起的事!
(为自己鼓个掌)
①左边 - ② 左边 = ① 右边 - ②右边
①
②
由①+②得: 5x=10
2x-5y=7 ①
2x+3y=-1 ②
由 ②-①得:8y=-8
问题8:自我提炼,方法总结?
若:同一未知数的系数相反
则:两式相加
若:同一未知数的系数相等
则:两式相减
从简化角度出发,利用消元手法
加减消元法
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做
加减消元法,简称加减法.
例1.指出下列方程组求解过程中有错误步骤
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
二元一次方程组
②
①
一元一次方程
11x=4.4
②- ①
两方程相减,消未知数y
x=0.4
解得x
y=0.2
例2.再议加减消元法
今天你学会了没有?
代入
②-①,得: 11x=4.4
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
总结:加减消元法解方程组基本思路是什么?主要步骤有哪些?
观察
同一个未知数的系
数相同或互为相反数
写解
检验
写出方程组的解
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
例3.选择你喜欢的方程组求解。
4s+3t=5
2s-t=-5
5x-6y=9
7x-4y=-5
设计简单说明:
精心设计问题串,促进知识自然生成;
围绕学生学习最近发展区,形成学习经验反差,诱发学习热情;
培养学生类比学习,知识迁移,学会总结,概念自然生成。
谢 谢
10.3 解二元一次方程组
问题1:怎样解下面的二元一次方程组呢?
①
②
代入①,消去 了!
把②变形得:
标准的代入消元法
问题2:还有其他办法求解吗?
①
②
简便的代入消元法
把②变形得
可以直接代入①呀!
问题3:根据上述方法,你还能优化出新解法吗?
①
②
认真观察式子特征
问题4:你发现什么式子特点?
和
互为相反数……
①
②
3x+5y +2x - 5y =10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
(3x + 5y)+(2x - 5y)= 21 + (-11)
等式性质
问题5:你有何策略消去未知数y吗?
问题6:新思路,新体验,你有什么感想?
整体相加
式子简化
思想:转化划归思想
特点:灵活巧妙
依据:等式的性质1
前提:观察式子结构
①
②
问题7:类比学习,你对下面的方程组的解法有什么新的见解?
学会知识迁移是一件了不起的事!
(为自己鼓个掌)
①左边 - ② 左边 = ① 右边 - ②右边
①
②
由①+②得: 5x=10
2x-5y=7 ①
2x+3y=-1 ②
由 ②-①得:8y=-8
问题8:自我提炼,方法总结?
若:同一未知数的系数相反
则:两式相加
若:同一未知数的系数相等
则:两式相减
从简化角度出发,利用消元手法
加减消元法
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做
加减消元法,简称加减法.
例1.指出下列方程组求解过程中有错误步骤
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
二元一次方程组
②
①
一元一次方程
11x=4.4
②- ①
两方程相减,消未知数y
x=0.4
解得x
y=0.2
例2.再议加减消元法
今天你学会了没有?
代入
②-①,得: 11x=4.4
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
总结:加减消元法解方程组基本思路是什么?主要步骤有哪些?
观察
同一个未知数的系
数相同或互为相反数
写解
检验
写出方程组的解
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
例3.选择你喜欢的方程组求解。
4s+3t=5
2s-t=-5
5x-6y=9
7x-4y=-5
设计简单说明:
精心设计问题串,促进知识自然生成;
围绕学生学习最近发展区,形成学习经验反差,诱发学习热情;
培养学生类比学习,知识迁移,学会总结,概念自然生成。
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
