高中数学人教A版(2019)必修 第二册 6.2平面向量的运算(1) 课件 (共38张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修 第二册 6.2平面向量的运算(1) 课件 (共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 745.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 10:30:26 | ||
图片预览







文档简介
(共38张PPT)
6.2平面向量的运算(1)
复习回顾
向量、零向量、单位向量、平行向量、相等向量的含义分别是什么?
复习回顾
向量、零向量、单位向量、平行向量、相等向量的含义分别是什么?
向量:既有大小又有方向的量
零向量:长度为0的向量
单位向量:长度等于1个单位长度的向量
平行向量:方向相同或相反的非零向量;规定:0与任意向量平行
相等向量:长度相等且方向相同的向量
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
猜想向量加法的运算律是什么?与数的运算律有什么不同?
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
类比数的加法,猜想向量的加法,应怎样定义向量的加法?
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
类比数的加法,猜想向量的加法,应怎样定义向量的加法?
类比矢量的合成,猜想向量的加法,应怎样定义向量的加法?
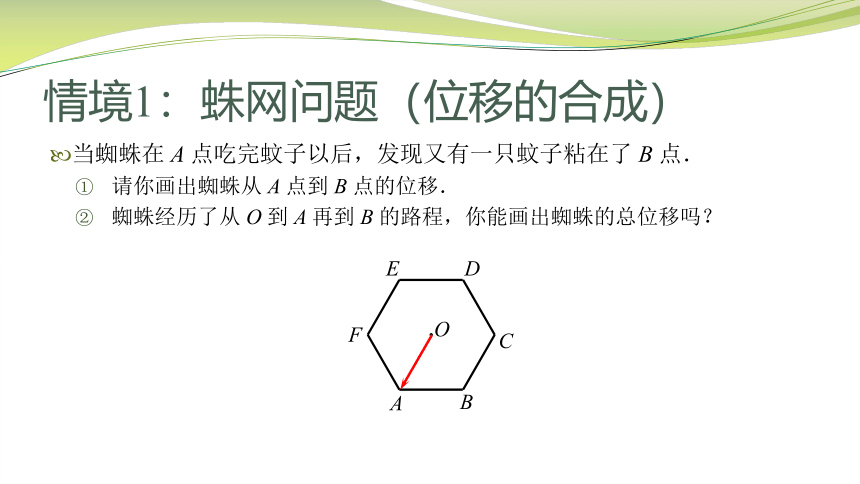
情境1:蛛网问题(位移的合成)
当蜘蛛在 A 点吃完蚊子以后,发现又有一只蚊子粘在了 B 点.
请你画出蜘蛛从 A 点到 B 点的位移.
蜘蛛经历了从 O 到 A 再到 B 的路程,你能画出蜘蛛的总位移吗?
A
O
B
C
D
E
F
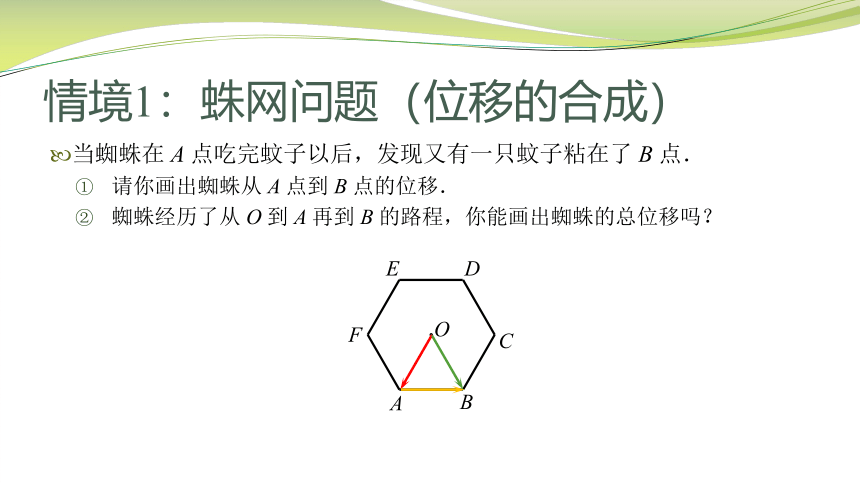
情境1:蛛网问题(位移的合成)
当蜘蛛在 A 点吃完蚊子以后,发现又有一只蚊子粘在了 B 点.
请你画出蜘蛛从 A 点到 B 点的位移.
蜘蛛经历了从 O 到 A 再到 B 的路程,你能画出蜘蛛的总位移吗?
A
O
B
C
D
E
F
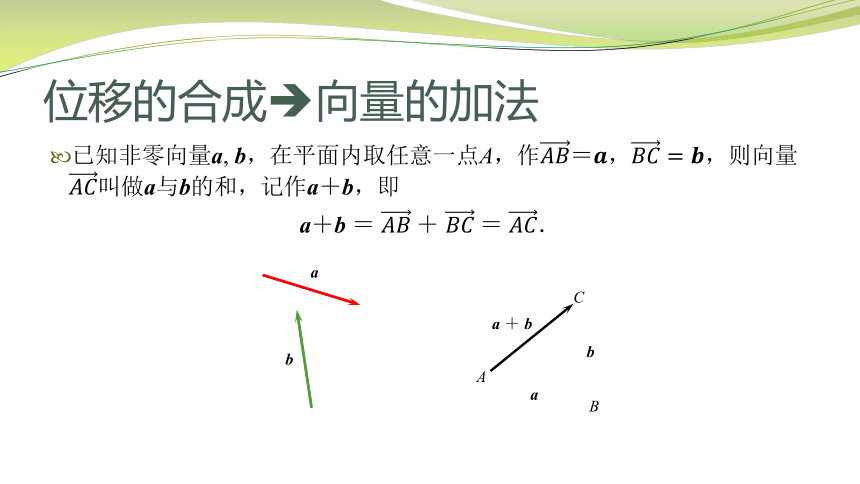
位移的合成 向量的加法
已知非零向量a, b,在平面内取任意一点A,作则向量叫做a与b的和,记作a+b,即
a+b = + = .
a
b
a
b
A
B
a + b
C
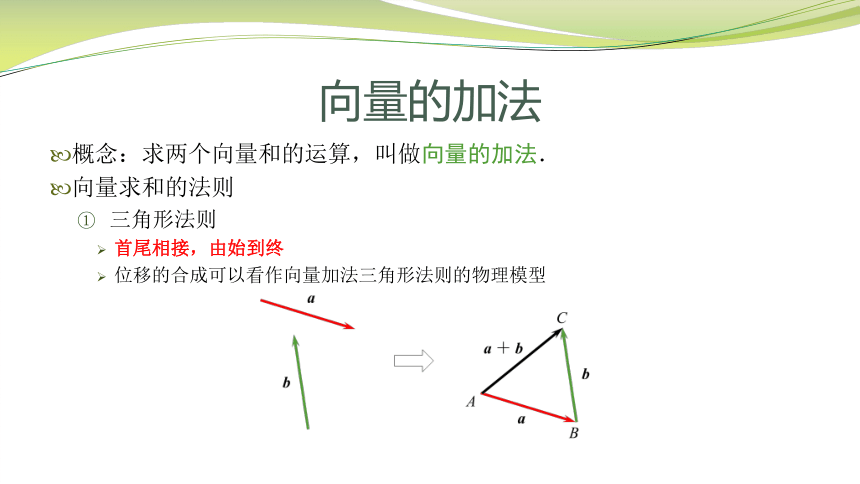
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
首尾相接,由始到终
位移的合成可以看作向量加法三角形法则的物理模型
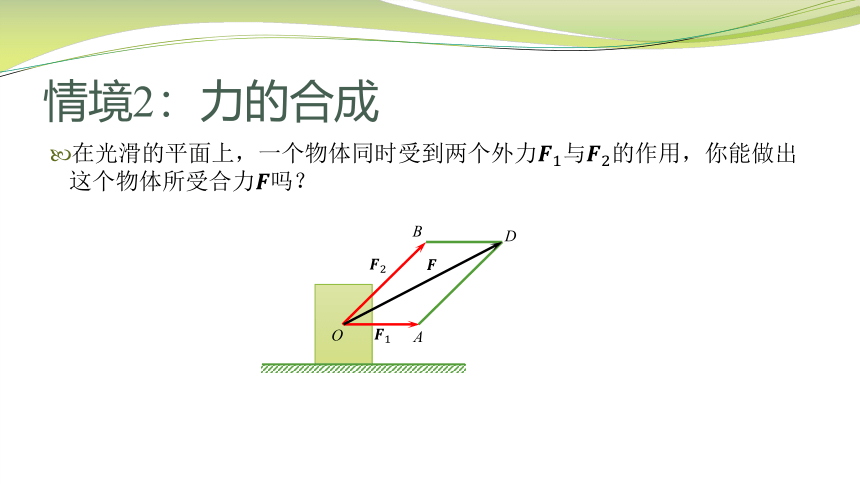
情境2:力的合成
在光滑的平面上,一个物体同时受到两个外力与的作用,你能做出这个物体所受合力吗?
O
A
B
D
力的合成 向量的加法
已知非零向量a, b,在平面内取任意一点A,作以AB, AC为邻边作□ABDC,则向量叫做a与b的和,记作a+b,即
a+b = + = .
a
b
a
b
A
B
a + b
C
D
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
首尾相连,由始到终
位移的合成可以看作向量加法三角形法则的物理模型
平行四边形法则
共起点,对角连
力的合成可以看作向量加法平行四边形法则的物理模型
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
平行四边形法则
对于零向量与任意向量a,我们规定
a + 0 = 0 + a = a.
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
a
b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
a
b
a
b
a + b
a
b
a + b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(2)
(3)
a
b
a
b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(2)
(3)
a
b
a
b
a
b
a + b
a
b
a + b
思考:向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法法则的应用
向量加法的平行四边形法则和三角形法则的区别和联系
区别 联系
三角形法则 (1) 首尾相接 (2) 适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1) 共起点 (2) 仅适用于不共线的两个向量求和 向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
(2)
(3)
探索:|a + b|, | a |, | b |之间的关系?
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
(2)
(3)
探索:|a + b|, | a |, | b |之间的关系?
一般地,我们有
|a + b| | a |+| b |,
当且仅当a, b方向相同时等号成立;
|a + b|,
当且仅当a, b方向相反时等号成立.
向量加法法则的应用
变式1 已知向量a, b, c,求作向量 a + b + c.
a
b
c
向量加法法则的应用
变式1 已知向量a, b, c,求作向量 a + b + c.
a
b
c
a
b
c
a + b + c
a
b
c
a + b + c
a + b
a + b
多个向量求和(多边形法则)
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
想一想
数的加法满足交换律、结合律,向量的加法是否也满足交换律和结合律呢?
数的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
向量的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
?
向量加法的运算律
向量加法的交换律:a + b = b + a
a
b
a + b
b
a
向量加法的运算律
向量加法的结合律:( a + b ) + c = a + ( b + c )
a
b
c
a + b
a + b + c
b + c
向量加法的运算律
向量的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
向量加法运算律的应用
例2 化简
(1)
(2) ;
(3)
向量加法运算律的应用
例2 化简
(1)
(2) ;
(3)
解 (1) 原式 ;
(2) 原式 ;
(3) 原式 .
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1) 用向量表示江水速度、船实际航行的速度;
A
北
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1) 用向量表示江水速度、船实际航行的速度;
解 (1) 表示船速, 表示江水速度,以AD, AB为邻边作□ABCD,
则表示船实际航行的速度.
A
北
A
B
D
C
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(2) 求船实际航行的速度的大小与方向(与江水速度间夹角的正切值).
A
B
D
C
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(2) 求船实际航行的速度的大小与方向(与江水速度间的夹角的正切值).
解 (2) 在Rt△ ABC中,, ,于是
.
因为tan CBA
故,船实际航行速度的大小为 km/h,方向与江水速度夹角的正切值为.
A
B
D
C
小结
内容
方法
小结
内容
一个概念:向量的加法,两个向量的和仍然是一个向量.
两个法则:向量加法的 三角形法则 和 平行四边形法则 .
一个不等式: |a + b| | a |+| b |
两条运算律:向量加法的 交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
方法
具体与抽象的数学思维方法
类比的思想方法
祝你学业进步!
6.2平面向量的运算(1)
复习回顾
向量、零向量、单位向量、平行向量、相等向量的含义分别是什么?
复习回顾
向量、零向量、单位向量、平行向量、相等向量的含义分别是什么?
向量:既有大小又有方向的量
零向量:长度为0的向量
单位向量:长度等于1个单位长度的向量
平行向量:方向相同或相反的非零向量;规定:0与任意向量平行
相等向量:长度相等且方向相同的向量
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
猜想向量加法的运算律是什么?与数的运算律有什么不同?
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
类比数的加法,猜想向量的加法,应怎样定义向量的加法?
研究问题
我们知道,数能进行运算,因为有了运算而使数的威力无穷.
向量能否也能像数一样进行运算呢?
类比数的加法,猜想向量的加法,应怎样定义向量的加法?
类比矢量的合成,猜想向量的加法,应怎样定义向量的加法?
情境1:蛛网问题(位移的合成)
当蜘蛛在 A 点吃完蚊子以后,发现又有一只蚊子粘在了 B 点.
请你画出蜘蛛从 A 点到 B 点的位移.
蜘蛛经历了从 O 到 A 再到 B 的路程,你能画出蜘蛛的总位移吗?
A
O
B
C
D
E
F
情境1:蛛网问题(位移的合成)
当蜘蛛在 A 点吃完蚊子以后,发现又有一只蚊子粘在了 B 点.
请你画出蜘蛛从 A 点到 B 点的位移.
蜘蛛经历了从 O 到 A 再到 B 的路程,你能画出蜘蛛的总位移吗?
A
O
B
C
D
E
F
位移的合成 向量的加法
已知非零向量a, b,在平面内取任意一点A,作则向量叫做a与b的和,记作a+b,即
a+b = + = .
a
b
a
b
A
B
a + b
C
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
首尾相接,由始到终
位移的合成可以看作向量加法三角形法则的物理模型
情境2:力的合成
在光滑的平面上,一个物体同时受到两个外力与的作用,你能做出这个物体所受合力吗?
O
A
B
D
力的合成 向量的加法
已知非零向量a, b,在平面内取任意一点A,作以AB, AC为邻边作□ABDC,则向量叫做a与b的和,记作a+b,即
a+b = + = .
a
b
a
b
A
B
a + b
C
D
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
首尾相连,由始到终
位移的合成可以看作向量加法三角形法则的物理模型
平行四边形法则
共起点,对角连
力的合成可以看作向量加法平行四边形法则的物理模型
向量的加法
概念:求两个向量和的运算,叫做向量的加法.
向量求和的法则
三角形法则
平行四边形法则
对于零向量与任意向量a,我们规定
a + 0 = 0 + a = a.
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
a
b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
a
b
a
b
a + b
a
b
a + b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(2)
(3)
a
b
a
b
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(2)
(3)
a
b
a
b
a
b
a + b
a
b
a + b
思考:向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法法则的应用
向量加法的平行四边形法则和三角形法则的区别和联系
区别 联系
三角形法则 (1) 首尾相接 (2) 适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1) 共起点 (2) 仅适用于不共线的两个向量求和 向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
(2)
(3)
探索:|a + b|, | a |, | b |之间的关系?
向量加法法则的应用
例1 在下列各小题中,已知向量a, b,求作向量 a + b .
(1)
(2)
(3)
探索:|a + b|, | a |, | b |之间的关系?
一般地,我们有
|a + b| | a |+| b |,
当且仅当a, b方向相同时等号成立;
|a + b|,
当且仅当a, b方向相反时等号成立.
向量加法法则的应用
变式1 已知向量a, b, c,求作向量 a + b + c.
a
b
c
向量加法法则的应用
变式1 已知向量a, b, c,求作向量 a + b + c.
a
b
c
a
b
c
a + b + c
a
b
c
a + b + c
a + b
a + b
多个向量求和(多边形法则)
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
想一想
数的加法满足交换律、结合律,向量的加法是否也满足交换律和结合律呢?
数的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
向量的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
?
向量加法的运算律
向量加法的交换律:a + b = b + a
a
b
a + b
b
a
向量加法的运算律
向量加法的结合律:( a + b ) + c = a + ( b + c )
a
b
c
a + b
a + b + c
b + c
向量加法的运算律
向量的加法运算律
交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
向量加法运算律的应用
例2 化简
(1)
(2) ;
(3)
向量加法运算律的应用
例2 化简
(1)
(2) ;
(3)
解 (1) 原式 ;
(2) 原式 ;
(3) 原式 .
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1) 用向量表示江水速度、船实际航行的速度;
A
北
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1) 用向量表示江水速度、船实际航行的速度;
解 (1) 表示船速, 表示江水速度,以AD, AB为邻边作□ABCD,
则表示船实际航行的速度.
A
北
A
B
D
C
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(2) 求船实际航行的速度的大小与方向(与江水速度间夹角的正切值).
A
B
D
C
向量加法的实际应用
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输,如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(2) 求船实际航行的速度的大小与方向(与江水速度间的夹角的正切值).
解 (2) 在Rt△ ABC中,, ,于是
.
因为tan CBA
故,船实际航行速度的大小为 km/h,方向与江水速度夹角的正切值为.
A
B
D
C
小结
内容
方法
小结
内容
一个概念:向量的加法,两个向量的和仍然是一个向量.
两个法则:向量加法的 三角形法则 和 平行四边形法则 .
一个不等式: |a + b| | a |+| b |
两条运算律:向量加法的 交换律 a + b = b + a
结合律 ( a + b ) + c = a + ( b + c )
方法
具体与抽象的数学思维方法
类比的思想方法
祝你学业进步!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
