2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.2导数的概念及其几何意义2课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.2导数的概念及其几何意义2课件(18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 14:28:38 | ||
图片预览


文档简介
(共18张PPT)
5.1.2 导数的概念及其几何意义
__________
复习回顾
1.导数(瞬时变化率)定义:
如果当 无限趋近于 0 时,平均变化率 无限趋近于一个确定的值,
即 有极限,则称_________________________,
并把这个确定的值叫做______________________(也称为__________ ) ,记作______或______.
用极限符号表示这个定义,就是__________________________________
y = f (x) 在x = x0处可导
瞬时变化率
y=f (x)在x=x0处的导数
第一步,写出 并化简;
第二步,求极限 , 若 存在,则
2.求函数 y=f (x)在 x=x0 处导数的步骤
探究新知
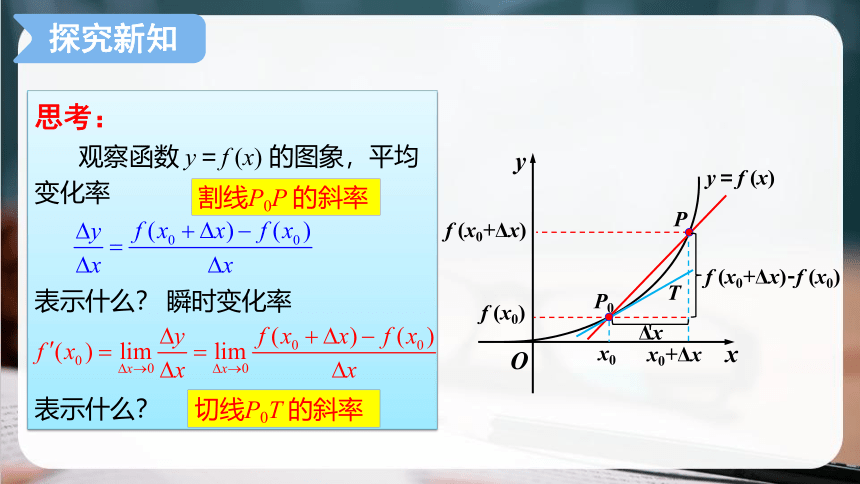
思考:
观察函数 y=f (x) 的图象,平均变化率
表示什么? 瞬时变化率
表示什么?
割线P0P 的斜率
切线P0T 的斜率
P0
x
y
O
y=f (x)
f (x0+Δx)
f (x0)
x0
x0+Δx
f (x0+Δx)-f (x0)
Δx
T
P
探究新知
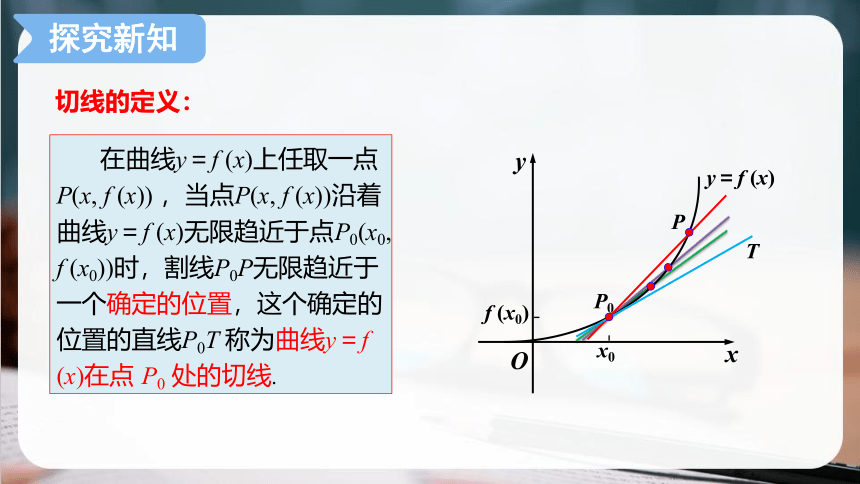
在曲线y=f (x)上任取一点P(x, f (x)) ,当点P(x, f (x))沿着曲线y=f (x)无限趋近于点P0(x0, f (x0))时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
x
y
O
y=f (x)
f (x0)
x0
T
切线的定义:
P0
P
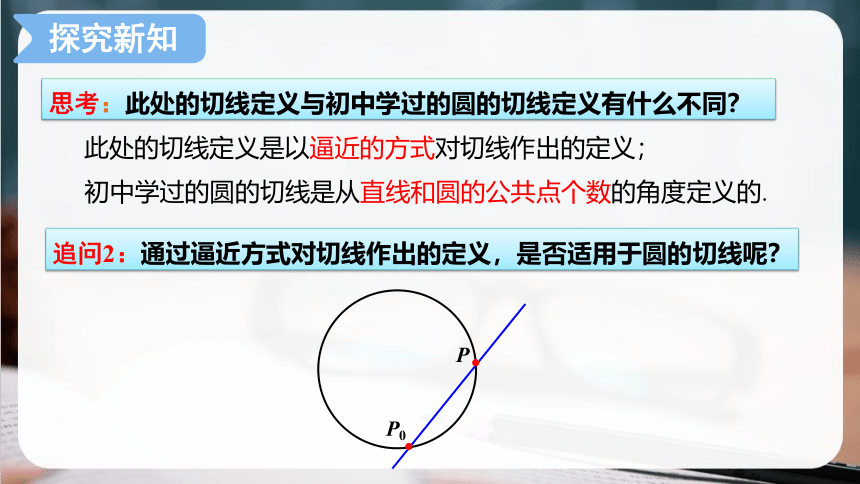
思考:此处的切线定义与初中学过的圆的切线定义有什么不同?
探究新知
初中学过的圆的切线是从直线和圆的公共点个数的角度定义的.
此处的切线定义是以逼近的方式对切线作出的定义;
追问2:通过逼近方式对切线作出的定义,是否适用于圆的切线呢?
P0
P
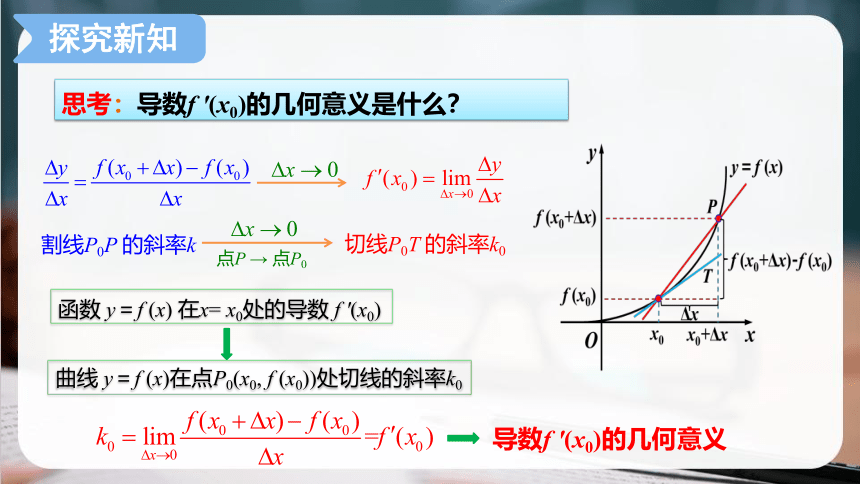
思考:导数f ′(x0)的几何意义是什么?
探究新知
割线P0P 的斜率k
切线P0T 的斜率k0
点P → 点P0
函数 y=f (x) 在x= x0处的导数 f ′(x0)
曲线 y=f (x)在点P0(x0, f (x0))处切线的斜率k0
导数f ′(x0)的几何意义
P
x
y
O
T
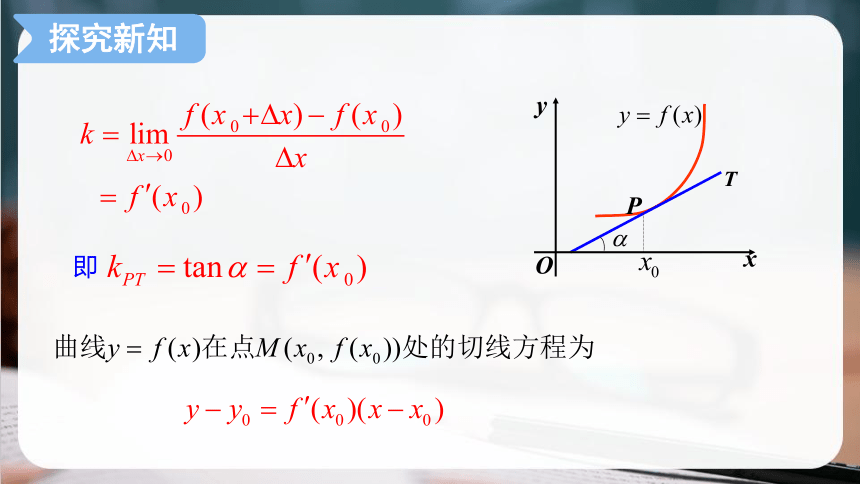
即
探究新知
1.求曲线y=-2x2+1在点(1,-1)处的切线方程.
小试牛刀
解:设f (x)=-2x2+1
所以所求切线方程为y-(-1)=(-4)(x-1), 即4x+y-3=0.
解决切线问题的关键: 利用导数的几何意义求出切线的斜率k0=f′(x0).
点斜式
探究新知
在点P0附近的曲线可以用点P0处的切线P0T 近似代替,这是微积分中重要的思想方法—以直代曲.
x
y
O
y=f (x)
f (x0)
x0
T
P0
P
思考:图中哪条直线最贴近点P0附近的曲线?
典例分析
例1 下图是高台跳水运动中运动员在运动过程中的重心相对于水面的高度随时间变化的函数h(t)=-4.9t2+4.8t+11的图象. 根据图象,请描述、比较曲线分别在t0, t1, t2 附近的变化情况.
在t0, t1, t2 附近的曲线
在t=t0, t1, t2处的切线
近似代替
斜率刻画
斜率的正负:增减趋势
斜率的大小:增减快慢
以直代曲
例2 如图表示人体血管中的药物浓c=f(t)(单位:mg/ml)随时间t (单位: min)变化的函数图像, 根据图像, 估计t=0.2,0.4,0.6,0.8(min)时,血管中药物浓度的瞬时变化率, 把数据用表格的形式列出.(精确到0.1)
典例分析
血管中药物浓度的瞬时变化率, 就是药物浓度.
函数f (t)在此时刻的导数,从图象上看,它表示曲线在该点处的切线的斜率.
数形结合以直代曲
以简单对象刻画复杂的对象
t 0.2 0.4 0.6 0.8
药物浓度的 瞬时变化率
下表给出了药物浓度瞬时变化率的估计值,
导函数的概念
探究新知
这也是求函数在点 x0 处的导数的方法之一.
(2)导函数 f′(x)是指某一区间内任意点x而言的,就是函数 f(x)的导数.
(3)函数 f(x)在点x0处的导数 f′(x0) 就是导函数 f′(x) 在x=x0处的函数值, .
f′(x0)与f′(x)的联系与区别
解1:
典例分析
解2:
典例分析
3.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学思想方法.
课堂小结
5.1.2 导数的概念及其几何意义
__________
复习回顾
1.导数(瞬时变化率)定义:
如果当 无限趋近于 0 时,平均变化率 无限趋近于一个确定的值,
即 有极限,则称_________________________,
并把这个确定的值叫做______________________(也称为__________ ) ,记作______或______.
用极限符号表示这个定义,就是__________________________________
y = f (x) 在x = x0处可导
瞬时变化率
y=f (x)在x=x0处的导数
第一步,写出 并化简;
第二步,求极限 , 若 存在,则
2.求函数 y=f (x)在 x=x0 处导数的步骤
探究新知
思考:
观察函数 y=f (x) 的图象,平均变化率
表示什么? 瞬时变化率
表示什么?
割线P0P 的斜率
切线P0T 的斜率
P0
x
y
O
y=f (x)
f (x0+Δx)
f (x0)
x0
x0+Δx
f (x0+Δx)-f (x0)
Δx
T
P
探究新知
在曲线y=f (x)上任取一点P(x, f (x)) ,当点P(x, f (x))沿着曲线y=f (x)无限趋近于点P0(x0, f (x0))时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
x
y
O
y=f (x)
f (x0)
x0
T
切线的定义:
P0
P
思考:此处的切线定义与初中学过的圆的切线定义有什么不同?
探究新知
初中学过的圆的切线是从直线和圆的公共点个数的角度定义的.
此处的切线定义是以逼近的方式对切线作出的定义;
追问2:通过逼近方式对切线作出的定义,是否适用于圆的切线呢?
P0
P
思考:导数f ′(x0)的几何意义是什么?
探究新知
割线P0P 的斜率k
切线P0T 的斜率k0
点P → 点P0
函数 y=f (x) 在x= x0处的导数 f ′(x0)
曲线 y=f (x)在点P0(x0, f (x0))处切线的斜率k0
导数f ′(x0)的几何意义
P
x
y
O
T
即
探究新知
1.求曲线y=-2x2+1在点(1,-1)处的切线方程.
小试牛刀
解:设f (x)=-2x2+1
所以所求切线方程为y-(-1)=(-4)(x-1), 即4x+y-3=0.
解决切线问题的关键: 利用导数的几何意义求出切线的斜率k0=f′(x0).
点斜式
探究新知
在点P0附近的曲线可以用点P0处的切线P0T 近似代替,这是微积分中重要的思想方法—以直代曲.
x
y
O
y=f (x)
f (x0)
x0
T
P0
P
思考:图中哪条直线最贴近点P0附近的曲线?
典例分析
例1 下图是高台跳水运动中运动员在运动过程中的重心相对于水面的高度随时间变化的函数h(t)=-4.9t2+4.8t+11的图象. 根据图象,请描述、比较曲线分别在t0, t1, t2 附近的变化情况.
在t0, t1, t2 附近的曲线
在t=t0, t1, t2处的切线
近似代替
斜率刻画
斜率的正负:增减趋势
斜率的大小:增减快慢
以直代曲
例2 如图表示人体血管中的药物浓c=f(t)(单位:mg/ml)随时间t (单位: min)变化的函数图像, 根据图像, 估计t=0.2,0.4,0.6,0.8(min)时,血管中药物浓度的瞬时变化率, 把数据用表格的形式列出.(精确到0.1)
典例分析
血管中药物浓度的瞬时变化率, 就是药物浓度.
函数f (t)在此时刻的导数,从图象上看,它表示曲线在该点处的切线的斜率.
数形结合以直代曲
以简单对象刻画复杂的对象
t 0.2 0.4 0.6 0.8
药物浓度的 瞬时变化率
下表给出了药物浓度瞬时变化率的估计值,
导函数的概念
探究新知
这也是求函数在点 x0 处的导数的方法之一.
(2)导函数 f′(x)是指某一区间内任意点x而言的,就是函数 f(x)的导数.
(3)函数 f(x)在点x0处的导数 f′(x0) 就是导函数 f′(x) 在x=x0处的函数值, .
f′(x0)与f′(x)的联系与区别
解1:
典例分析
解2:
典例分析
3.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学思想方法.
课堂小结
