2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题2课件(13张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题2课件(13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 14:30:32 | ||
图片预览




文档简介
(共13张PPT)
5.1.1 变化率问题
__________
物体运动的平均速度
物体运动的瞬时速度
无限逼近
取极限
复习引入
(1) 平均速度:
(2) 瞬时速度:
几何意义?
1.瞬时速度的本质是平均速度的极限.
2.求物体在时刻t0的瞬时速度一般步骤:
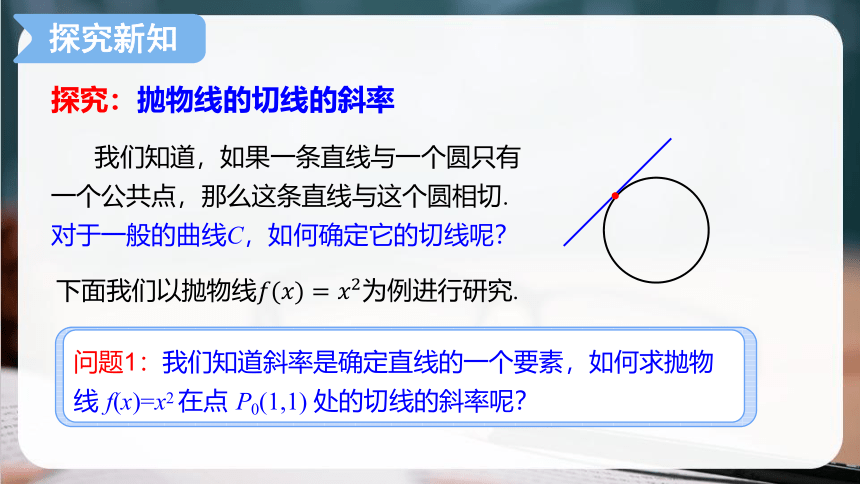
探究:抛物线的切线的斜率
探究新知
我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切.
对于一般的曲线C,如何确定它的切线呢?
下面我们以抛物线为例进行研究.
问题1:我们知道斜率是确定直线的一个要素,如何求抛物线 f(x)=x2 在点 P0(1,1) 处的切线的斜率呢?
追问1:如果一条直线与一条曲线只有一个公共点,那么这条直线与这条曲线一定相切吗?
探究新知
追问2:如果一条直线与一条曲线相切,那么它们只有一个公共点吗?
因此,我们不能像研究直线和圆的位置关系那样,通过交点的个数来定义相切了.
不一定
不一定
探究新知
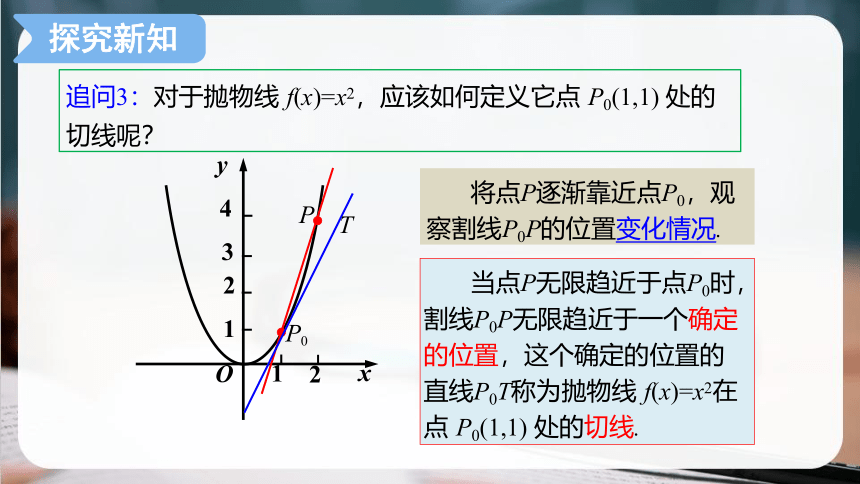
追问3:对于抛物线 f(x)=x2,应该如何定义它点 P0(1,1) 处的切线呢?
几何意义:函数图象上过点 (1,h(1))和点(1+Δt, h(1+Δt))的直线斜率
类比上节课的研究思路,例如研究运动员在 t =1s的瞬时速度
几何意义是什么?
探究新知
x
y
O
1
2
1
2
3
4
P
P0
将点P逐渐靠近点P0,观察割线P0P的位置变化情况.
T
当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T称为抛物线 f(x)=x2在点 P0(1,1) 处的切线.
追问3:对于抛物线 f(x)=x2,应该如何定义它点 P0(1,1) 处的切线呢?
追问4:如何求抛物线 f(x)=x2在点 P0(1,1) 处的切线P0T 的斜率k0呢?
探究新知
割线位置
切线位置
无限逼近
割线斜率
切线斜率
无限逼近
取极限
记点P的横坐标 x=1+Δx,则点P的坐标即为 (1+Δx,(1+Δx)2).
于是割线P0P 的斜率
让横坐标变化量 Δx趋近于0,观察割线斜率的变化情况.
探究新知
当Δx无限趋近于0,割线斜率k无限趋近于2.
探究新知
我们把2叫做“当Δx无限趋近于0时, 的极限“,记为
从几何图形上看,当横坐标间隔| Δx |无限变小时, 当点P无限趋近于点P0时,割线P0P无限趋近于点P0处的切线P0T .
割线P0P的斜率k 无限趋近于点P0处的切线的斜率k0.
因此,切线P0T 的斜率k0=2.
x
y
O
1
2
1
2
3
4
P
P0
T
探究新知
x
y
O
1
2
1
2
3
4
P0
记点P的横坐标 x=2+Δx,则点P的坐标即为 (2+Δx,(2+Δx) 2).于是割线P0P 的斜率
故抛物线 f(x)=x2在点 P0(2,4) 处的切线P0T 的斜率为4.
问题2:你能用上述方法,求抛物线 f(x)=x2在点 P0(2,4) 处的切线P0T 的斜率吗?
P
探究新知
x
y
O
1
2
1
2
3
4
P0
记点P的横坐标 x= x0+Δx,则点P的坐标即为 (x0 +Δx,(x0 +Δx)2).于是割线P0P 的斜率
故抛物线 f(x)=x2在点 P0(x0, x02) 处的切线P0T 的斜率为2x0.
问题3:一般地,如何求抛物线 f(x)=x2在点 P0(x0, x02) 处的切线P0T 的斜率呢?
P
切线斜率的本质是瞬时变化率
小试牛刀
1.已知抛物线 f(x)=x2+1. 求:
(1)抛物线在点(0,1) 处的切线的斜率;
(2)抛物线在点(0,1) 处的切线方程.
解:(1)
故抛物线在点(0,1) 处的切线的斜率为0.
(2)抛物线在点(0,1) 处的切线方程为 y =1.
物体运动的平均速度
物体运动的瞬时速度
函数的平均变化率
函数的瞬时变化率
几何意义
割线的斜率
几何意义
切线的斜率
无限逼近
无限逼近
课堂小结
5.1.1 变化率问题
__________
物体运动的平均速度
物体运动的瞬时速度
无限逼近
取极限
复习引入
(1) 平均速度:
(2) 瞬时速度:
几何意义?
1.瞬时速度的本质是平均速度的极限.
2.求物体在时刻t0的瞬时速度一般步骤:
探究:抛物线的切线的斜率
探究新知
我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切.
对于一般的曲线C,如何确定它的切线呢?
下面我们以抛物线为例进行研究.
问题1:我们知道斜率是确定直线的一个要素,如何求抛物线 f(x)=x2 在点 P0(1,1) 处的切线的斜率呢?
追问1:如果一条直线与一条曲线只有一个公共点,那么这条直线与这条曲线一定相切吗?
探究新知
追问2:如果一条直线与一条曲线相切,那么它们只有一个公共点吗?
因此,我们不能像研究直线和圆的位置关系那样,通过交点的个数来定义相切了.
不一定
不一定
探究新知
追问3:对于抛物线 f(x)=x2,应该如何定义它点 P0(1,1) 处的切线呢?
几何意义:函数图象上过点 (1,h(1))和点(1+Δt, h(1+Δt))的直线斜率
类比上节课的研究思路,例如研究运动员在 t =1s的瞬时速度
几何意义是什么?
探究新知
x
y
O
1
2
1
2
3
4
P
P0
将点P逐渐靠近点P0,观察割线P0P的位置变化情况.
T
当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T称为抛物线 f(x)=x2在点 P0(1,1) 处的切线.
追问3:对于抛物线 f(x)=x2,应该如何定义它点 P0(1,1) 处的切线呢?
追问4:如何求抛物线 f(x)=x2在点 P0(1,1) 处的切线P0T 的斜率k0呢?
探究新知
割线位置
切线位置
无限逼近
割线斜率
切线斜率
无限逼近
取极限
记点P的横坐标 x=1+Δx,则点P的坐标即为 (1+Δx,(1+Δx)2).
于是割线P0P 的斜率
让横坐标变化量 Δx趋近于0,观察割线斜率的变化情况.
探究新知
当Δx无限趋近于0,割线斜率k无限趋近于2.
探究新知
我们把2叫做“当Δx无限趋近于0时, 的极限“,记为
从几何图形上看,当横坐标间隔| Δx |无限变小时, 当点P无限趋近于点P0时,割线P0P无限趋近于点P0处的切线P0T .
割线P0P的斜率k 无限趋近于点P0处的切线的斜率k0.
因此,切线P0T 的斜率k0=2.
x
y
O
1
2
1
2
3
4
P
P0
T
探究新知
x
y
O
1
2
1
2
3
4
P0
记点P的横坐标 x=2+Δx,则点P的坐标即为 (2+Δx,(2+Δx) 2).于是割线P0P 的斜率
故抛物线 f(x)=x2在点 P0(2,4) 处的切线P0T 的斜率为4.
问题2:你能用上述方法,求抛物线 f(x)=x2在点 P0(2,4) 处的切线P0T 的斜率吗?
P
探究新知
x
y
O
1
2
1
2
3
4
P0
记点P的横坐标 x= x0+Δx,则点P的坐标即为 (x0 +Δx,(x0 +Δx)2).于是割线P0P 的斜率
故抛物线 f(x)=x2在点 P0(x0, x02) 处的切线P0T 的斜率为2x0.
问题3:一般地,如何求抛物线 f(x)=x2在点 P0(x0, x02) 处的切线P0T 的斜率呢?
P
切线斜率的本质是瞬时变化率
小试牛刀
1.已知抛物线 f(x)=x2+1. 求:
(1)抛物线在点(0,1) 处的切线的斜率;
(2)抛物线在点(0,1) 处的切线方程.
解:(1)
故抛物线在点(0,1) 处的切线的斜率为0.
(2)抛物线在点(0,1) 处的切线方程为 y =1.
物体运动的平均速度
物体运动的瞬时速度
函数的平均变化率
函数的瞬时变化率
几何意义
割线的斜率
几何意义
切线的斜率
无限逼近
无限逼近
课堂小结
