2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值(2)课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值(2)课件(18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 14:37:04 | ||
图片预览





文档简介
(共18张PPT)
5.3.2 函数的极值与最大(小)值(2)
__________
如果在 x0 附近的左侧f '(x)>0, 右侧f '(x)<0 ,那么 f (x0)为极大值;
解方程 f '(x) = 0. 当 f '(x0) = 0 时:
如果在 x0 附近的左侧f '(x)<0, 右侧f '(x)>0 ,那么 f (x0)为极小值.
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M 满足:
(1)对于任意的x∈I,都有f(x)≤M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最大值.
一般地,设函数y=f(x)的定义域为I ,如果存在实数M 满足:
(2)对于任意的x∈I ,都有f(x)≥M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最小值 .
复习回顾
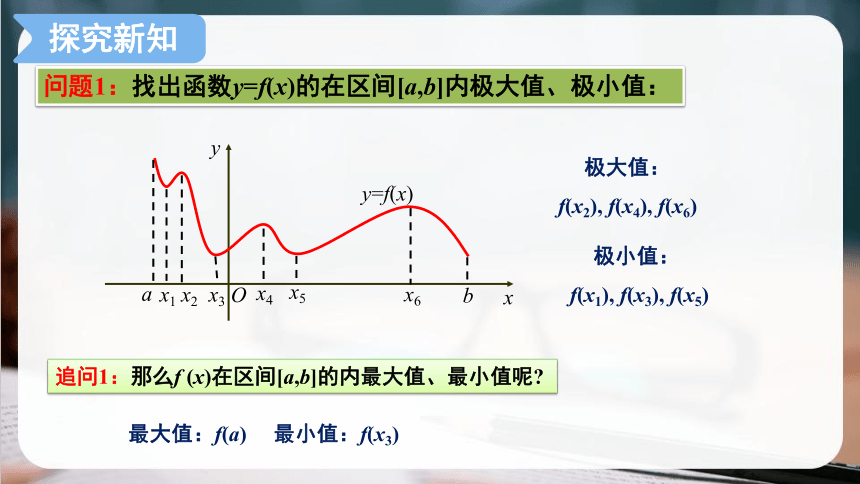
问题1:找出函数y=f(x)的在区间[a,b]内极大值、极小值:
追问1:那么f (x)在区间[a,b]的内最大值、最小值呢
极大值:
f(x2), f(x4), f(x6)
极小值:
f(x1), f(x3), f(x5)
最大值:f(a) 最小值:f(x3)
探究新知
x
O
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
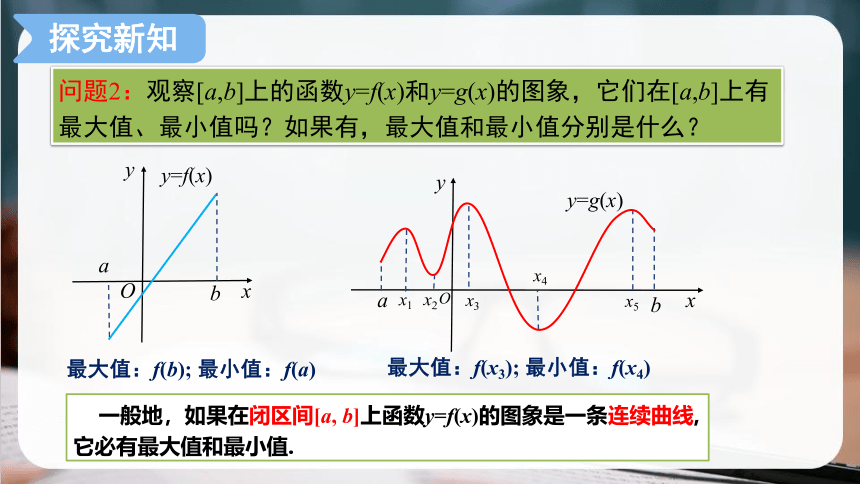
问题2:观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
x
y
O
a
b
y=f(x)
x
y
O
a
b
x2
x1
x3
x4
x5
y=g(x)
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
一般地,如果在闭区间[a, b]上函数y=f(x)的图象是一条连续曲线,它必有最大值和最小值.
探究新知
追问1:函数最值与极值有什么关系?
求最值的方法:只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
1.函数的最大值、最小值是比较整个定义域上的函数值得出的,函数的极大值、极小值是比较极值点附近的函数值得出的.
2.函数的极值可以有多个,但函数在其定义域上的最大值、最小值最多各有一个.
3.极值只能在区间内取得,最值则可以在端点处取得;有最值未必有极值;极值有可能成为最值,最值只要不在端点处取得必定是极值.
探究新知
追问2:为什么给定函数的区间必须是闭区间?
因为不能保证f(x)在开区间上有最大值和最小值(最值有可能在区间端点处取得).
探究新知
O
x
y
a
b
y=f(x)
y=f(x)
O
x
y
a
b
O
x
y
a
b
y=f(x)
O
x
y
a
b
y=f(x)
例1 求 在[0,3]的最大值与最小值.
又因为f(0)=4,f(3)=1
典例分析
解:因为
x (0, 2) 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以,当x=0,时函数f(x)在[0,3]上取得最大值4,
当x=2时,函数f(x)在[0,3]上取得最小值 .
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
方法归纳
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
巩固练习
1.求下列函数在给定区间上的最大值与最小值:
解: (1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
巩固练习
1.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (1)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
典例分析
所以,当x=1时, f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以, f(x) ≥ f(1)=0, 即
解:将不等式 转化为
设 ,那么
令 ,解得
故当x>0时, .
除点(1,0)外,曲线C1: 在 y 轴右侧的部分位于曲线C2 :y=lnx的下方.
巩固练习
所以,当x=1时, f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以, f(x) ≥ f(1)=0, 即x-lnx-1≥0
解:将不等式lnx≤ x-1转化为x-lnx-1≥0
令 ,解得
故当x>0时, lnx≤ x-1.
x
y
O
y=x-1
y=lnx
除点(1,0)外,曲线C1:y=x-1
在 y 轴右侧的部分位于曲线C2 :y=lnx的上方.
设f(x)= x-lnx-1,那么f ′(x)= 1-
例3 给定.
(1)判断函数的单调性,并求出的极值;
(2)画出函数的大致图象;
(3)求出方程= ()的解的个数.
解:(1)函数的定义域为
所以,在区间上单调递减,在区间上单调递增.
当时,有极小值=
典例分析
x (-∞, -2) -2 (-2, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
当、的变化情况如表所示:
令f '(x) =0,解得:
因为f '(x)=(x+1)'ex+(x+1)(ex)'=ex+(x+1)ex =(x+2)ex
(2)令=0,解得:
当时, 0; 当时, 0.
所以的图象经过特殊点A( ), B,C.
当时, 与一次函数相比, 指数函数 呈爆炸性增长, 从而
当时, ,
根据以上信息,我们画出的大致图象如图所示:
(3)方程=()的解的个数为函数的图象与直线的交点个数.
由(1)及图可得,当时,有最小值
所以,方程= 的解得个数有如下结论;
当< 时,解为0个;
当 或时,解为1个;
当<0时,解为2个.
f (x)=(x+1)ex
x
y
O
1
1
-1
-2
-1
(1)求出函数f(x)的定义域;
(2)求导数f '(x)及函数f '(x)的零点;
(3)用零点将f(x) 定义域为若干个区间,列表给出f '(x)在各个区间上的正负,并得出f(x)单调性与极值;
(4)确定f(x)图象经过的一些特殊点,以及图象的变化趋势;
(5)画出f(x)的大致图象.
方法归纳
通常可以按如下步骤画出函数f(x)的大致图象:
例3 某制造商制造并出售球形瓶装的某种饮料,瓶子的制造成本是分,其 (单位:cm)中是瓶子的半径,已知每出售1mL的饮料制造商可获得0.2分,且制造商能制作的瓶子的最大半径是6cm.
(1)瓶子半径多大时,能使每瓶饮料的利润最大
(2)瓶子半径多大时,每瓶饮料的利润最小
典例分析
问题:饮料瓶大小对饮料公司利润的影响
(1)你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些?你想从数学上知道它的道理吗?
(2)是不是饮料瓶越大,饮料公司的利润越大?
我们利用导数工具来解决这个问题.
解:由题意可知,每瓶饮料的利润是
=
所以,令0,解得=2.
当时,<0;当时,0.
因此,当半径>2时,0 ,单调递增,即半径越大,利润越高;当半径2时,<0,单调递减,即半径越大,利润越低.
(1)半径为6cm时,利润最大
(2)半径2cm时,利润最小,这时<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润时负值.
换一个角度:如果我们不用导数工具,直接从函数f(r)的图象上观察,你有什么发现?
r
y
O
3
2
1
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
课堂小结
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
5.3.2 函数的极值与最大(小)值(2)
__________
如果在 x0 附近的左侧f '(x)>0, 右侧f '(x)<0 ,那么 f (x0)为极大值;
解方程 f '(x) = 0. 当 f '(x0) = 0 时:
如果在 x0 附近的左侧f '(x)<0, 右侧f '(x)>0 ,那么 f (x0)为极小值.
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M 满足:
(1)对于任意的x∈I,都有f(x)≤M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最大值.
一般地,设函数y=f(x)的定义域为I ,如果存在实数M 满足:
(2)对于任意的x∈I ,都有f(x)≥M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最小值 .
复习回顾
问题1:找出函数y=f(x)的在区间[a,b]内极大值、极小值:
追问1:那么f (x)在区间[a,b]的内最大值、最小值呢
极大值:
f(x2), f(x4), f(x6)
极小值:
f(x1), f(x3), f(x5)
最大值:f(a) 最小值:f(x3)
探究新知
x
O
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
问题2:观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
x
y
O
a
b
y=f(x)
x
y
O
a
b
x2
x1
x3
x4
x5
y=g(x)
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
一般地,如果在闭区间[a, b]上函数y=f(x)的图象是一条连续曲线,它必有最大值和最小值.
探究新知
追问1:函数最值与极值有什么关系?
求最值的方法:只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
1.函数的最大值、最小值是比较整个定义域上的函数值得出的,函数的极大值、极小值是比较极值点附近的函数值得出的.
2.函数的极值可以有多个,但函数在其定义域上的最大值、最小值最多各有一个.
3.极值只能在区间内取得,最值则可以在端点处取得;有最值未必有极值;极值有可能成为最值,最值只要不在端点处取得必定是极值.
探究新知
追问2:为什么给定函数的区间必须是闭区间?
因为不能保证f(x)在开区间上有最大值和最小值(最值有可能在区间端点处取得).
探究新知
O
x
y
a
b
y=f(x)
y=f(x)
O
x
y
a
b
O
x
y
a
b
y=f(x)
O
x
y
a
b
y=f(x)
例1 求 在[0,3]的最大值与最小值.
又因为f(0)=4,f(3)=1
典例分析
解:因为
x (0, 2) 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以,当x=0,时函数f(x)在[0,3]上取得最大值4,
当x=2时,函数f(x)在[0,3]上取得最小值 .
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
方法归纳
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
巩固练习
1.求下列函数在给定区间上的最大值与最小值:
解: (1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
巩固练习
1.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (1)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
典例分析
所以,当x=1时, f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以, f(x) ≥ f(1)=0, 即
解:将不等式 转化为
设 ,那么
令 ,解得
故当x>0时, .
除点(1,0)外,曲线C1: 在 y 轴右侧的部分位于曲线C2 :y=lnx的下方.
巩固练习
所以,当x=1时, f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以, f(x) ≥ f(1)=0, 即x-lnx-1≥0
解:将不等式lnx≤ x-1转化为x-lnx-1≥0
令 ,解得
故当x>0时, lnx≤ x-1.
x
y
O
y=x-1
y=lnx
除点(1,0)外,曲线C1:y=x-1
在 y 轴右侧的部分位于曲线C2 :y=lnx的上方.
设f(x)= x-lnx-1,那么f ′(x)= 1-
例3 给定.
(1)判断函数的单调性,并求出的极值;
(2)画出函数的大致图象;
(3)求出方程= ()的解的个数.
解:(1)函数的定义域为
所以,在区间上单调递减,在区间上单调递增.
当时,有极小值=
典例分析
x (-∞, -2) -2 (-2, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
当、的变化情况如表所示:
令f '(x) =0,解得:
因为f '(x)=(x+1)'ex+(x+1)(ex)'=ex+(x+1)ex =(x+2)ex
(2)令=0,解得:
当时, 0; 当时, 0.
所以的图象经过特殊点A( ), B,C.
当时, 与一次函数相比, 指数函数 呈爆炸性增长, 从而
当时, ,
根据以上信息,我们画出的大致图象如图所示:
(3)方程=()的解的个数为函数的图象与直线的交点个数.
由(1)及图可得,当时,有最小值
所以,方程= 的解得个数有如下结论;
当< 时,解为0个;
当 或时,解为1个;
当<0时,解为2个.
f (x)=(x+1)ex
x
y
O
1
1
-1
-2
-1
(1)求出函数f(x)的定义域;
(2)求导数f '(x)及函数f '(x)的零点;
(3)用零点将f(x) 定义域为若干个区间,列表给出f '(x)在各个区间上的正负,并得出f(x)单调性与极值;
(4)确定f(x)图象经过的一些特殊点,以及图象的变化趋势;
(5)画出f(x)的大致图象.
方法归纳
通常可以按如下步骤画出函数f(x)的大致图象:
例3 某制造商制造并出售球形瓶装的某种饮料,瓶子的制造成本是分,其 (单位:cm)中是瓶子的半径,已知每出售1mL的饮料制造商可获得0.2分,且制造商能制作的瓶子的最大半径是6cm.
(1)瓶子半径多大时,能使每瓶饮料的利润最大
(2)瓶子半径多大时,每瓶饮料的利润最小
典例分析
问题:饮料瓶大小对饮料公司利润的影响
(1)你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些?你想从数学上知道它的道理吗?
(2)是不是饮料瓶越大,饮料公司的利润越大?
我们利用导数工具来解决这个问题.
解:由题意可知,每瓶饮料的利润是
=
所以,令0,解得=2.
当时,<0;当时,0.
因此,当半径>2时,0 ,单调递增,即半径越大,利润越高;当半径2时,<0,单调递减,即半径越大,利润越低.
(1)半径为6cm时,利润最大
(2)半径2cm时,利润最小,这时<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润时负值.
换一个角度:如果我们不用导数工具,直接从函数f(r)的图象上观察,你有什么发现?
r
y
O
3
2
1
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
课堂小结
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
