同底数的幂的乘法 )
图片预览






文档简介
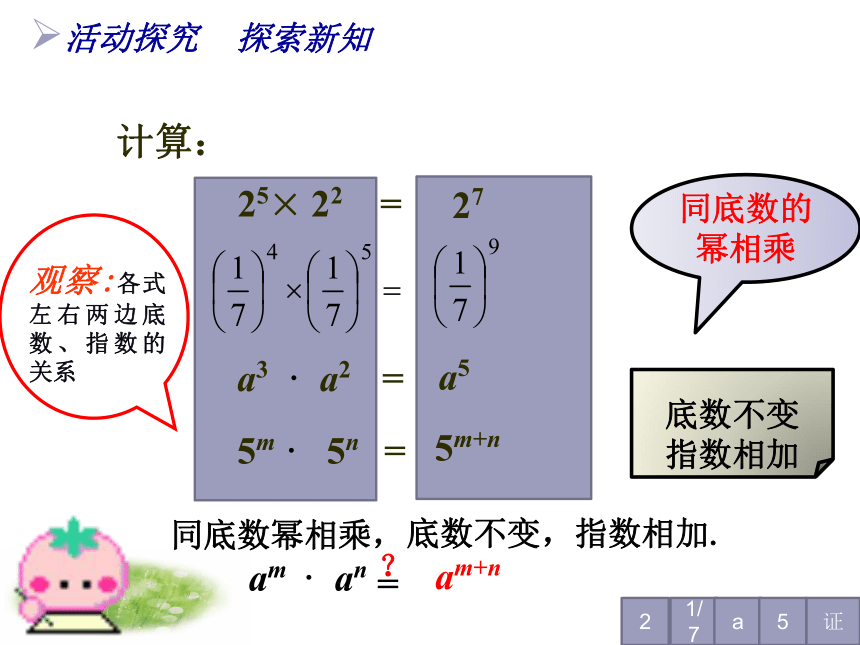
课件25张PPT。同底数幂的乘法 义务教育人教版《数学》八年级上册同底数幂的乘法同底数幂的乘法同底数幂的乘法同底数幂的乘法整式乘法——银河-1号巨型计算机 银河-1号巨型计算机 创设情境 新知导入 曙光5000A高性能计算机,它每秒可进行3× 1015次运算,若工作105秒可进行多少次运算? 1015 × 105=等于多少呢? ?3 × 1015 × 105( )活动探究 探索新知25× 22 =计算:a3 · a2 =
2721/7a5
5m+n5m · 5n =
am · an
底数不变
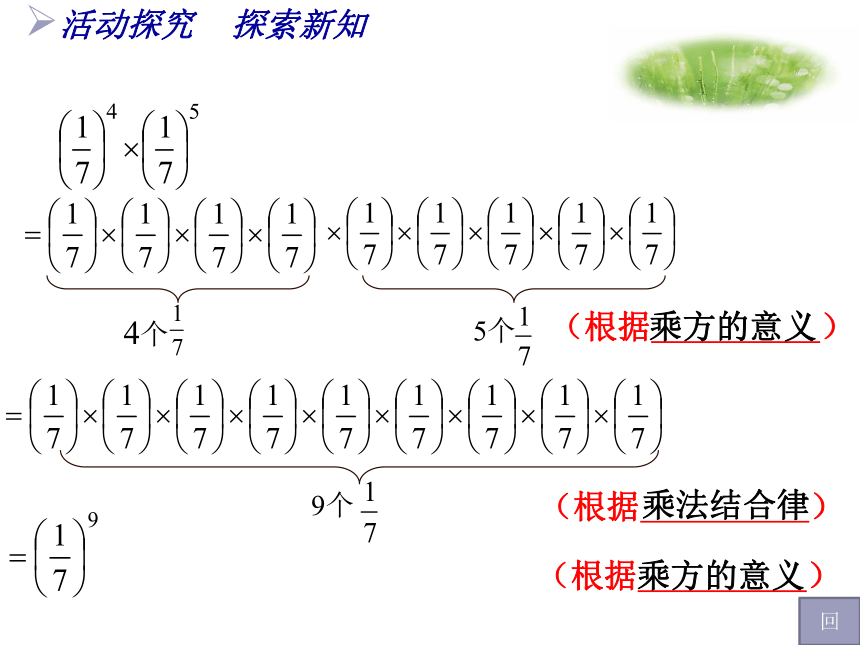
指数相加同底数的幂相乘=am+n证a5同底数幂相乘,底数不变,指数相加.?活动探究 探索新知=(2×2×2×2×2)×(2×2)5个22个2(根据 )乘方的意义=2×2×2×2×2×2×27个2(根据 )乘法结合律=27 (根据 )乘方的意义25× 22=2725× 22回活动探究 探索新知4个5个9个(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义回2019年2月3日19时44分a3 · a2活动探究 探索新知=(a · a · a ) · ( a · a )3个a(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义2个a= a · a · a · a · a5个a=a5 回5m · 5n活动探究 探索新知= (5×5…×5) ×( 5×5 …×5 )m个5n个5=5×5×5 …×5(m+n)个5=5m+n(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义回n个a(aa…a)am· an=am+n (m,n都是正整数) 即am·an = am+n (m,n都是正整数)(乘方的意义)m个a(m+n)个a= aa…a(aa…a)(乘法结合律)(乘方的意义)活动探究 探索新知验证: am· an==am+n am · an = am+n (m,n都是正整数)同底数幂相乘,底数 ,指数 .不变相加如: 46×49=46+9=415活动探究 探索新知同底数幂的乘法性质: 曙光5000A高性能计算机,它每秒可进行3× 1015次运算,若工作105秒可进行多少次运算? 3 ×(1015 × 105)=3 ×1015+5=3 ×1020三个或三个以上的同底数幂相乘,此性质仍然成立.am · an = am+n (m,n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有类似的性质呢? 怎样用公式表示?底数 ,指数 .不变相加 如: am·an·ap = am+n+p (m,n,p都是正整数)活动探究 探索新知同底数幂的乘法性质:计算:(1) x5 · x3;巩固新知 尝试训练★小试牛刀(3) 23×2×25;
(2) a6 · a;
(5) y · y2+n· y3-n;
(6) (y -1)·(y-1)2+n·( y-1)3-n.
底数、指数可以是一个具体的数或字母,也可以是一个单项式或多项式.am· an = am+n (4) xm · xm+1;
巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x-y)3·(x-y)2+ n.
第2关
判断 :
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9×34×27; (2) (-2)12·23+n .
第1关
口答:
(1) m4 · m3; (2)5m · 5m+1 ;
(3) 33×3×35; (4) (x-y) 3·(x-y)2+ n.巩固新知 尝试训练★智勇闯关巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x-y) 3·(x-y)2+ n.
第2关
判断:
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9×34×27; (2) (-2)12·23+n.
(1) x3·x5=x15 ( ); 巩固新知 尝试训练 ★智勇闯关
第2关只要底数相同的幂就可以做乘法:底数不变,指数相加×××判断:(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x -y) 3·(x-y)2+ n.
第2关
判断:
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9 ×34×27; (2) (-2)12·23+n.
化成同底:
(-2)12=212
巩固新知 尝试训练 ★智勇闯关第3关(1) 9 ×34×27;(2) (-2)12·23+n .化成同底:27=33
9=32计算:.变式训练: (-2)13·23+n巩固新知 自我检测计算:同底数幂相乘,
底数 指数
am·an = am+n
(m, n都是正整数)我学到了什么? 知识 方法 “特殊→一般→特殊”
例子 公式 应用不变,相加.回顾反思 知识小结 若8×4 = 2x+1,求x 的值.知识拓展 发展思维 1.P142练习
P148 习题15.1 1.(1)(2) 2.(1) 2.思考题:
计算:
1+21+22+23+24+25+26+27+28+29-210 作业:欢迎指导
谢 谢同底幂的乘法同底幂的乘法同底幂的乘法同底幂的乘法同底数幂的乘法湖北省宜昌市第九中学 褚艳娟
2721/7a5
5m+n5m · 5n =
am · an
底数不变
指数相加同底数的幂相乘=am+n证a5同底数幂相乘,底数不变,指数相加.?活动探究 探索新知=(2×2×2×2×2)×(2×2)5个22个2(根据 )乘方的意义=2×2×2×2×2×2×27个2(根据 )乘法结合律=27 (根据 )乘方的意义25× 22=2725× 22回活动探究 探索新知4个5个9个(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义回2019年2月3日19时44分a3 · a2活动探究 探索新知=(a · a · a ) · ( a · a )3个a(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义2个a= a · a · a · a · a5个a=a5 回5m · 5n活动探究 探索新知= (5×5…×5) ×( 5×5 …×5 )m个5n个5=5×5×5 …×5(m+n)个5=5m+n(根据 )乘方的意义(根据 )乘法结合律(根据 )乘方的意义回n个a(aa…a)am· an=am+n (m,n都是正整数) 即am·an = am+n (m,n都是正整数)(乘方的意义)m个a(m+n)个a= aa…a(aa…a)(乘法结合律)(乘方的意义)活动探究 探索新知验证: am· an==am+n am · an = am+n (m,n都是正整数)同底数幂相乘,底数 ,指数 .不变相加如: 46×49=46+9=415活动探究 探索新知同底数幂的乘法性质: 曙光5000A高性能计算机,它每秒可进行3× 1015次运算,若工作105秒可进行多少次运算? 3 ×(1015 × 105)=3 ×1015+5=3 ×1020三个或三个以上的同底数幂相乘,此性质仍然成立.am · an = am+n (m,n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有类似的性质呢? 怎样用公式表示?底数 ,指数 .不变相加 如: am·an·ap = am+n+p (m,n,p都是正整数)活动探究 探索新知同底数幂的乘法性质:计算:(1) x5 · x3;巩固新知 尝试训练★小试牛刀(3) 23×2×25;
(2) a6 · a;
(5) y · y2+n· y3-n;
(6) (y -1)·(y-1)2+n·( y-1)3-n.
底数、指数可以是一个具体的数或字母,也可以是一个单项式或多项式.am· an = am+n (4) xm · xm+1;
巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x-y)3·(x-y)2+ n.
第2关
判断 :
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9×34×27; (2) (-2)12·23+n .
第1关
口答:
(1) m4 · m3; (2)5m · 5m+1 ;
(3) 33×3×35; (4) (x-y) 3·(x-y)2+ n.巩固新知 尝试训练★智勇闯关巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x-y) 3·(x-y)2+ n.
第2关
判断:
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9×34×27; (2) (-2)12·23+n.
(1) x3·x5=x15 ( ); 巩固新知 尝试训练 ★智勇闯关
第2关只要底数相同的幂就可以做乘法:底数不变,指数相加×××判断:(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .巩固新知 尝试训练★智勇闯关第1关
口答:
(1) m4 · m3; (2) 5m · 5m+1 ;
(3) 33×3×35; (4) (x -y) 3·(x-y)2+ n.
第2关
判断:
(1)x3·x5=x15 ( );(2) x3·x3=2x6 ( );(3) b7+b7=b14 ( ) .
第3关
计算:
(1) 9 ×34×27; (2) (-2)12·23+n.
化成同底:
(-2)12=212
巩固新知 尝试训练 ★智勇闯关第3关(1) 9 ×34×27;(2) (-2)12·23+n .化成同底:27=33
9=32计算:.变式训练: (-2)13·23+n巩固新知 自我检测计算:同底数幂相乘,
底数 指数
am·an = am+n
(m, n都是正整数)我学到了什么? 知识 方法 “特殊→一般→特殊”
例子 公式 应用不变,相加.回顾反思 知识小结 若8×4 = 2x+1,求x 的值.知识拓展 发展思维 1.P142练习
P148 习题15.1 1.(1)(2) 2.(1) 2.思考题:
计算:
1+21+22+23+24+25+26+27+28+29-210 作业:欢迎指导
谢 谢同底幂的乘法同底幂的乘法同底幂的乘法同底幂的乘法同底数幂的乘法湖北省宜昌市第九中学 褚艳娟
