苏科版七年级数学下册 8.1 同底数幂的乘法 教案(表格式)
文档属性
| 名称 | 苏科版七年级数学下册 8.1 同底数幂的乘法 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 28.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 15:13:26 | ||
图片预览

文档简介
8.1同底数幂的乘法
教学内容 8.1同底数幂的乘法
教学目标 知识与能力 掌握同底数幂的乘法法则,学生能灵活地运用法则进行计算;
过程与方法 在了解同底数幂的乘法运算的意义的基础上,“发现” 同底数幂的乘法性质,培养学生观察、概括和抽象的能力
情感与态度 培养学生观察、概括与抽象的能力。
教学重点 熟悉同底数幂的乘法性质、幂的意义和乘法运算律等内容
教学难点 区分幂的意义与乘法的意义,发展学生的推理能力和有条理的表达能力。
教具学具 多媒体课件 电子白板
教学过程 教师活动 学生活动 设计意图
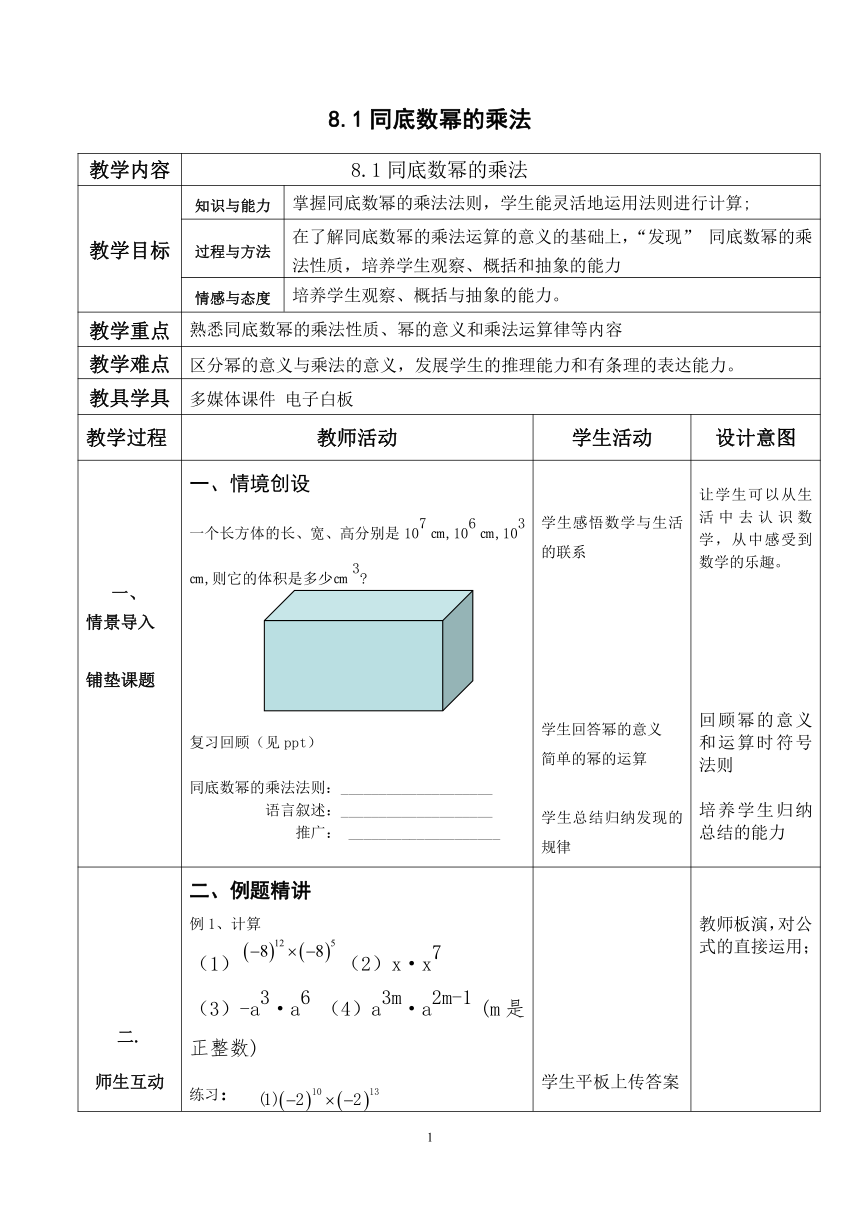
一、 情景导入 铺垫课题 一、情境创设 一个长方体的长、宽、高分别是107㎝,106㎝,103㎝,则它的体积是多少㎝3 复习回顾(见ppt) 同底数幂的乘法法则:____________________ 语言叙述:____________________ 推广: ____________________ 学生感悟数学与生活的联系 学生回答幂的意义 简单的幂的运算 学生总结归纳发现的规律 让学生可以从生活中去认识数学,从中感受到数学的乐趣。 回顾幂的意义和运算时符号法则 培养学生归纳总结的能力
二. 师生互动 探索研究 二、例题精讲 例1、计算 (1) (2)x·x7 (3)-a3·a6 (4)a3m·a2m-1 (m是正整数) 练习: (3) 25×23×24 例2、计算 (1) (-x)2·(-x3) (2) (-a2) ·(-a) 3 练习:计算: (1) a7·(-a)6; (2) (-n)4·(-n3) (3) (-y) ·y2·(-y)3 例3、计算,结果用幂的形式表示 (1)(2y+1)2 · (2y+1)5; (2)(x-y)5 · (y-x)2; (3)a4·a6+a5·a5. 练习:计算 1.(a-b)(a-b)3(a-b)2 2.(m-n)(n-m)4(m-n)3 3.an·an+1+a2n·a(n是正整数) 迁移应用: 填空; (1)a3·a( )=a8 (2)a4·_____·a2=a10 (3)若a4·am=a10,则m=____ (4)若x·xa·x4=x2a+3,则a=____. 幂的乘法的逆应用:____________________ 巩固练习: 1.已知am=2,an=3,求am+n的值; 2.已知3x+1=81,求x. 3、如果地球卫星绕地球运行速度是 ,求卫星运行1h的路程。 学生平板上传答案 教师点评学生答案中存在问题 学生回答,注意符号;教师点评学生答案中存在问题 学生上台板演; 教师点评。 学生思考、尝试回答;教师点评答案,分析,让学生找出规律,总结。 学生练习,回答问题。 教师板演,对公式的直接运用; 巩固所学知识,强化同底数幂乘法法则的应用 教师板演,对公式的运用中的幂的符号的处理。 教师板演,对公式的运用中的整体思想的运用。 教师引导学生找出答案规律,得出同底数幂的运算法则的逆运算。 教师点评
三、 归纳总结 知识回顾 课堂小结 本节课你学到了什么? 学生讨论,积极思考,踊跃发言。 培养学生归纳总结的能力。
四、 布置作业 学生课后练习 及时巩固课堂所学
3
教学内容 8.1同底数幂的乘法
教学目标 知识与能力 掌握同底数幂的乘法法则,学生能灵活地运用法则进行计算;
过程与方法 在了解同底数幂的乘法运算的意义的基础上,“发现” 同底数幂的乘法性质,培养学生观察、概括和抽象的能力
情感与态度 培养学生观察、概括与抽象的能力。
教学重点 熟悉同底数幂的乘法性质、幂的意义和乘法运算律等内容
教学难点 区分幂的意义与乘法的意义,发展学生的推理能力和有条理的表达能力。
教具学具 多媒体课件 电子白板
教学过程 教师活动 学生活动 设计意图
一、 情景导入 铺垫课题 一、情境创设 一个长方体的长、宽、高分别是107㎝,106㎝,103㎝,则它的体积是多少㎝3 复习回顾(见ppt) 同底数幂的乘法法则:____________________ 语言叙述:____________________ 推广: ____________________ 学生感悟数学与生活的联系 学生回答幂的意义 简单的幂的运算 学生总结归纳发现的规律 让学生可以从生活中去认识数学,从中感受到数学的乐趣。 回顾幂的意义和运算时符号法则 培养学生归纳总结的能力
二. 师生互动 探索研究 二、例题精讲 例1、计算 (1) (2)x·x7 (3)-a3·a6 (4)a3m·a2m-1 (m是正整数) 练习: (3) 25×23×24 例2、计算 (1) (-x)2·(-x3) (2) (-a2) ·(-a) 3 练习:计算: (1) a7·(-a)6; (2) (-n)4·(-n3) (3) (-y) ·y2·(-y)3 例3、计算,结果用幂的形式表示 (1)(2y+1)2 · (2y+1)5; (2)(x-y)5 · (y-x)2; (3)a4·a6+a5·a5. 练习:计算 1.(a-b)(a-b)3(a-b)2 2.(m-n)(n-m)4(m-n)3 3.an·an+1+a2n·a(n是正整数) 迁移应用: 填空; (1)a3·a( )=a8 (2)a4·_____·a2=a10 (3)若a4·am=a10,则m=____ (4)若x·xa·x4=x2a+3,则a=____. 幂的乘法的逆应用:____________________ 巩固练习: 1.已知am=2,an=3,求am+n的值; 2.已知3x+1=81,求x. 3、如果地球卫星绕地球运行速度是 ,求卫星运行1h的路程。 学生平板上传答案 教师点评学生答案中存在问题 学生回答,注意符号;教师点评学生答案中存在问题 学生上台板演; 教师点评。 学生思考、尝试回答;教师点评答案,分析,让学生找出规律,总结。 学生练习,回答问题。 教师板演,对公式的直接运用; 巩固所学知识,强化同底数幂乘法法则的应用 教师板演,对公式的运用中的幂的符号的处理。 教师板演,对公式的运用中的整体思想的运用。 教师引导学生找出答案规律,得出同底数幂的运算法则的逆运算。 教师点评
三、 归纳总结 知识回顾 课堂小结 本节课你学到了什么? 学生讨论,积极思考,踊跃发言。 培养学生归纳总结的能力。
四、 布置作业 学生课后练习 及时巩固课堂所学
3
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
