2021-2022学年人教版七年级数学下册5.2.2平行线的判定课后培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线的判定课后培优(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 13:41:43 | ||
图片预览


文档简介
平行线的判定
一、单选题
1.下列语句正确的个数是( )
(1)经过平面内一点有且只有一条直线与已知直线垂直;
(2)经过平面内一点有且只有一条直线与已知直线平行;
(3)在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(4)在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线也互相平行.
A.1个 B.2个 C.3个 D.4个
2.如图,能判定直线的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠1=∠4
3.如图所示,点E在BA的延长线上,点F在BC的延长线上,则下列条件中能判定AB∥CD的是( )
A.∠1=∠2 B.∠DAE=∠B
C.∠D+∠BCD=180° D.∠3=∠4
4.如图,下列条件中不能判定的是( )
A. B. C. D.
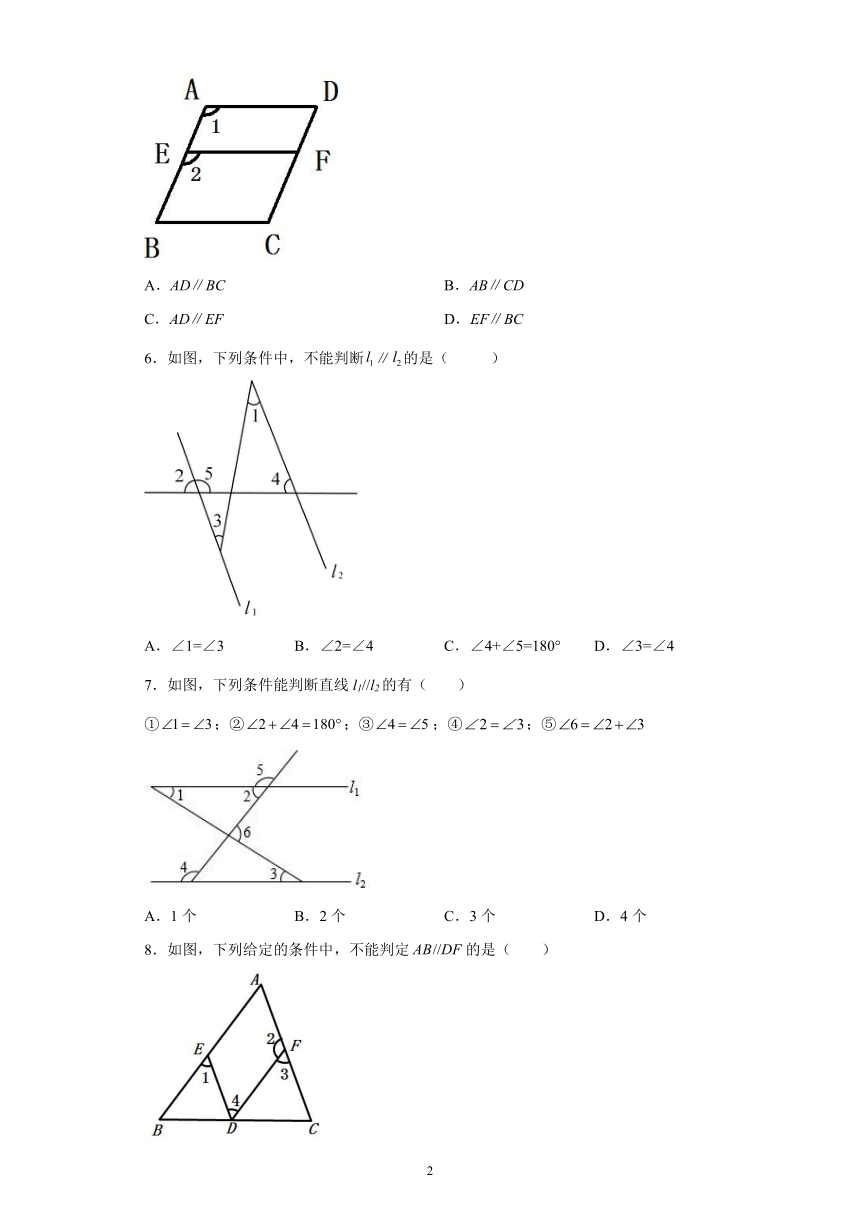
5.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
6.如图,下列条件中,不能判断∥的是( )
A.∠1=∠3 B.∠2=∠4 C.∠4+∠5=180° D.∠3=∠4
7.如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
8.如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
9.如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
10.如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
11.一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°.
B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°.
D.第一次向右拐140°,第二次向左拐40°.
二、多选题
12.如图,下列条件中,能判断直线a∥b的是( )
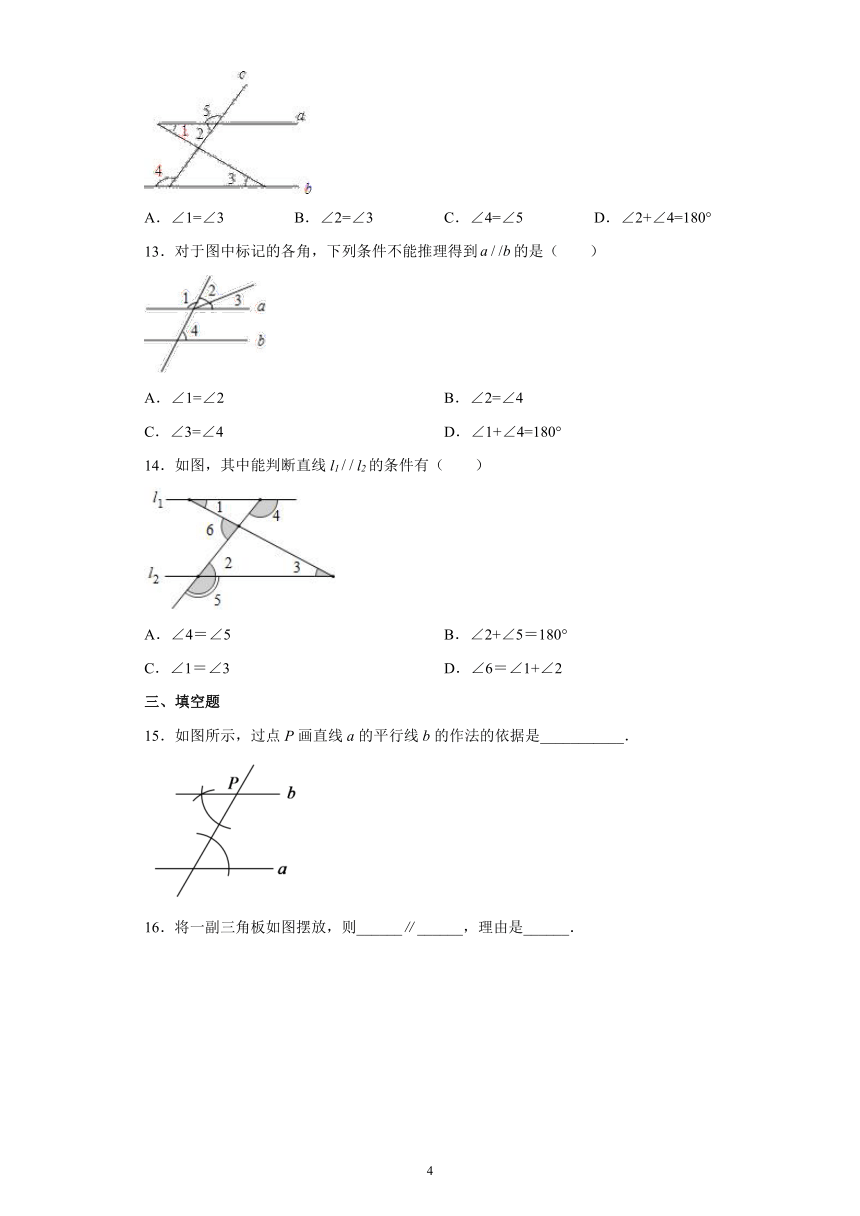
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
13.对于图中标记的各角,下列条件不能推理得到的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
14.如图,其中能判断直线l1l2的条件有( )
A.∠4=∠5 B.∠2+∠5=180°
C.∠1=∠3 D.∠6=∠1+∠2
三、填空题
15.如图所示,过点P画直线a的平行线b的作法的依据是___________.
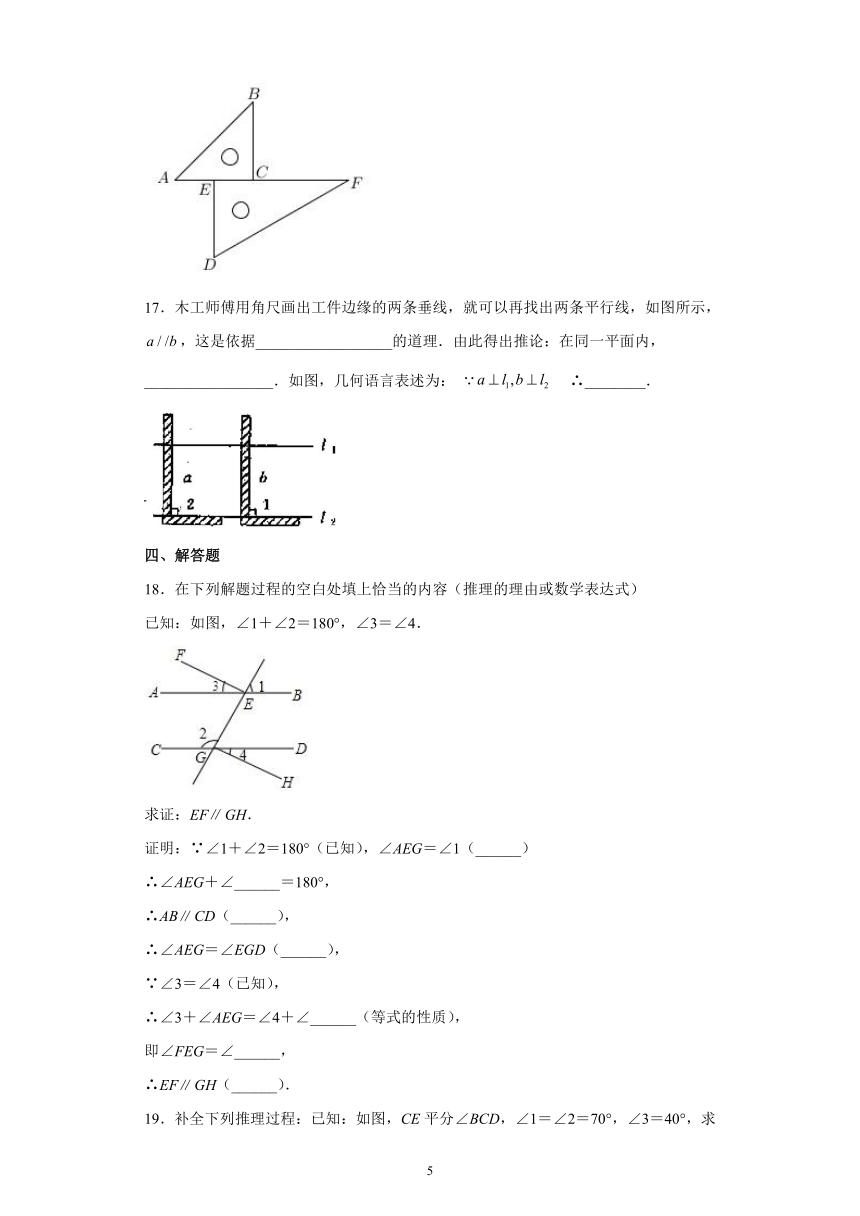
16.将一副三角板如图摆放,则______∥______,理由是______.
17.木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示, ,这是依据__________________的道理.由此得出推论:在同一平面内,_________________.如图,几何语言表述为: ∴________.
四、解答题
18.在下列解题过程的空白处填上恰当的内容(推理的理由或数学表达式)
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EFGH.
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(______)
∴∠AEG+∠______=180°,
∴ABCD(______),
∴∠AEG=∠EGD(______),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠______(等式的性质),
即∠FEG=∠______,
∴EFGH(______).
19.补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
20.如图所示,已知平分,求证: .
21.已知:如图,∠ADE=∠DEF,∠EFC+∠C=180°,请判断AD与 BC之间的关系,请说明理由.
22.如图,,平分,平分,.
(1)求证:;
(2)与平行吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:经过平面内一点有且只有一条直线与已知直线垂直,故(1)正确;
经过直线外一点有且只有一条直线与已知直线平行,故(2)不正确;
平面内,平行具有传递性,故(3)正确;
同一平面内,如果两条直线都与第三条直线垂直,则同位角(内错角)相等,这两条直线互相平行,故(4)正确,
∴正确的有(1)、(3)、(4),
故选:C.
2.D
解:我们根据两直线相交,对顶角相等得知∠3=∠4恒成立,此选项为干扰项.根据平行线判定定理,我们可以知道,∠1+∠2=180°(同旁内角互补,两直线平行);∠1=∠3(内错角相等,两直线平行),∠1=∠4(同位角相等,两直线平行),我们可以知道D为正确答案.
故答案为:D.
3.D
解:A、当∠1=∠2时,可得:AD∥BC,故本选项不合题意;
B、当∠DAE=∠B时,可得AD∥BC,故本选项不合题意;
C、当∠D+∠BCD=180°时,可得:AD∥BC,故本选项不合题意;
D、当∠3=∠4时,可得:AB∥CD,故本选项符合题意;
故选:D
4.A
解:A、∵∠1=∠2,∠1+∠3=∠2+∠5=180°,
∴∠3=∠5,
因为”同旁内角互补,两直线平行“,
所以本选项不能判断AB∥CD;
B、∵∠3=∠4,
∴AB∥CD,
故本选项能判定AB∥CD;
C、∵,
∴AB∥CD,
故本选项能判定AB∥CD;
D、∵∠1=∠5,
∴AB∥CD,
故本选项能判定AB∥CD;
故选:A.
5.C
解:略
6.D
解:、,内错角相等,
,故本选项错误,不符合题意;
、,同位角相等,
,故本选项错误,不符合题意;
、,同旁内角互补,
,故本选项错误,不符合题意;
、,它们不是内错角或同位角,
与的关系无法判定,故本选项正确,符合题意.
故选:D.
7.D
解:①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
8.A
解:A选项:当∠1=∠A时,可知是DE和AC被AB所截得到的同位角,可得到DE∥AC,而不是AB∥DF,故符合题意;
B选项:当∠A=∠3时,可知是AB、DF被AC所截得到的同位角,可得AB∥DF,故不符合题意;
C选项:当∠1=∠4时,可知是AB、DF被DE所截得到的内错角,可得AB∥DF,故不符合题意;
D选项:当∠2+∠A=180°时,是一对同旁内角,可得AB∥DF;故不符合题意;
故选A.
9.D
解:根据内错角相等,两直线平行,
∵∠A=∠2,
∴AB∥CD,
故选:D.
10.A
解:由图形得,有两个相等的同位角,所以依据为:同位角相等,两直线平行.
故选:A.
11.B
解:A.如图,由内错角相等可知,第二次拐弯后与原来平行,但方向相反,故不符合题意;
B.如图,由同位角相等可知,第二次拐弯后与原来平行,且方向相同,故符合题意;
C.如图,由内错角不相等可知,第二次拐弯后与原来不平行,故不符合题意;
D.如图,由同位角不相等可知,第二次拐弯后与原来不平行,故不符合题意.
故选:B.
12.ACD
解:A、∵,∴,内错角相等,两直线平行,符合题意;
B、,无法判定,不符合题意;
C、∵∠4=∠5,∴,同位角相等,两直线平行,符合题意;
D、∵,∴,同旁内角互补,两直线平行,符合题意;
故选ACD
13.ABC
解:A、∠1=∠2,因为它们不是,被截得的同位角或内错角,符合题意;
B、∠2=∠4,因为它们不是,被截得的同位角或内错角,符合题意;
C、∠3=∠4,因为它们不是,被截得的同位角或内错角,符合题意;
D、∠1+∠4=180°,∠1的对顶角与∠4是,被截得的同旁内角,能推理得到,不符合题意.
故选:ABC.
14.ACD
解:A∵∠4=∠5,
∴l1∥l2,故本条件符合题意;
B由∠2+∠5=180°不能得到l1∥l2,故本条件符合题意;
C∵∠1=∠3,
∴l1∥l2,故本条件符合题意;
D∵∠6=∠2+∠3=∠1+∠2,
∴∠1=∠3,
∴l1∥l2,故本条件符合题意.
故选ACD.
15.内错角相等,两直线平行
解:由作图可知,
,
(内错角相等两直线平行),
故答案为:内错角相等,两直线平行.
16. 内错角相等,两直线平行
解:一副三角板如图摆放,
∴,
∴(内错角相等,两直线平行),
故答案为:;;内错角相等,两直线平行.
17. 同位角相等,两直线平行 垂直于同一直线的两条直线互相平行
解:,
,(同位角相等,两直线平行)
由此得出推论:
在同一平面内,垂直于同一直线的两条直线互相平行,
几何语言表述为:
,
∴,
故答案为:同位角相等,两直线平行;垂直于同一直线的两条直线互相平行;.
18.对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
解:证明:∵∠1+∠2=180°(已知),∠AEG=∠1(对顶角相等)
∴∠AEG+∠2=180°,
∴ABCD(同旁内角互补,两直线平行),
∴∠AEG=∠EGD(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠EGD(等式性质),
即∠FEG=∠EGH
∴EFGH(内错角相等,两直线平行)
故答案为:对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
19.见解析
解:证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
20.证明见解析.
解:
∵OF平分∠EOD (已知)
∴∠EOD =2∠FOD(角平分线的性质)
又∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠AGE=130°(已知)
∴∠AGO=50°(平角的定义)
∴∠EOD=∠AGO
∴AB//CD(内错角相等,两直线平行)
21.AD∥BC,理由见解析.
解:AD∥BC,理由如下:
∵∠ADE=∠DEF,∠EFC+∠C=180°,
∴AD∥EF,EF∥BC,
∴AD∥BC.
22.(1)见解析;(2),理由见解析.
解:(1)∵BE平分,平分,
∴,,
∵∠ABC=∠ADC ,
∴∠2=∠CDF,
∵∠1=∠2 ,
∴∠1=∠CDF,,
∴AB∥CD;
(2)AD∥BC,理由如下:
∵AB∥CD,
∴,
∵∠ABC=∠ADC ,
∴∠ADC+∠C=180°,
∴AD∥BC
答案第1页,共2页
一、单选题
1.下列语句正确的个数是( )
(1)经过平面内一点有且只有一条直线与已知直线垂直;
(2)经过平面内一点有且只有一条直线与已知直线平行;
(3)在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(4)在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线也互相平行.
A.1个 B.2个 C.3个 D.4个
2.如图,能判定直线的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠1=∠4
3.如图所示,点E在BA的延长线上,点F在BC的延长线上,则下列条件中能判定AB∥CD的是( )
A.∠1=∠2 B.∠DAE=∠B
C.∠D+∠BCD=180° D.∠3=∠4
4.如图,下列条件中不能判定的是( )
A. B. C. D.
5.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
6.如图,下列条件中,不能判断∥的是( )
A.∠1=∠3 B.∠2=∠4 C.∠4+∠5=180° D.∠3=∠4
7.如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
8.如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
9.如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
10.如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
11.一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°.
B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°.
D.第一次向右拐140°,第二次向左拐40°.
二、多选题
12.如图,下列条件中,能判断直线a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
13.对于图中标记的各角,下列条件不能推理得到的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
14.如图,其中能判断直线l1l2的条件有( )
A.∠4=∠5 B.∠2+∠5=180°
C.∠1=∠3 D.∠6=∠1+∠2
三、填空题
15.如图所示,过点P画直线a的平行线b的作法的依据是___________.
16.将一副三角板如图摆放,则______∥______,理由是______.
17.木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示, ,这是依据__________________的道理.由此得出推论:在同一平面内,_________________.如图,几何语言表述为: ∴________.
四、解答题
18.在下列解题过程的空白处填上恰当的内容(推理的理由或数学表达式)
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EFGH.
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(______)
∴∠AEG+∠______=180°,
∴ABCD(______),
∴∠AEG=∠EGD(______),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠______(等式的性质),
即∠FEG=∠______,
∴EFGH(______).
19.补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
20.如图所示,已知平分,求证: .
21.已知:如图,∠ADE=∠DEF,∠EFC+∠C=180°,请判断AD与 BC之间的关系,请说明理由.
22.如图,,平分,平分,.
(1)求证:;
(2)与平行吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:经过平面内一点有且只有一条直线与已知直线垂直,故(1)正确;
经过直线外一点有且只有一条直线与已知直线平行,故(2)不正确;
平面内,平行具有传递性,故(3)正确;
同一平面内,如果两条直线都与第三条直线垂直,则同位角(内错角)相等,这两条直线互相平行,故(4)正确,
∴正确的有(1)、(3)、(4),
故选:C.
2.D
解:我们根据两直线相交,对顶角相等得知∠3=∠4恒成立,此选项为干扰项.根据平行线判定定理,我们可以知道,∠1+∠2=180°(同旁内角互补,两直线平行);∠1=∠3(内错角相等,两直线平行),∠1=∠4(同位角相等,两直线平行),我们可以知道D为正确答案.
故答案为:D.
3.D
解:A、当∠1=∠2时,可得:AD∥BC,故本选项不合题意;
B、当∠DAE=∠B时,可得AD∥BC,故本选项不合题意;
C、当∠D+∠BCD=180°时,可得:AD∥BC,故本选项不合题意;
D、当∠3=∠4时,可得:AB∥CD,故本选项符合题意;
故选:D
4.A
解:A、∵∠1=∠2,∠1+∠3=∠2+∠5=180°,
∴∠3=∠5,
因为”同旁内角互补,两直线平行“,
所以本选项不能判断AB∥CD;
B、∵∠3=∠4,
∴AB∥CD,
故本选项能判定AB∥CD;
C、∵,
∴AB∥CD,
故本选项能判定AB∥CD;
D、∵∠1=∠5,
∴AB∥CD,
故本选项能判定AB∥CD;
故选:A.
5.C
解:略
6.D
解:、,内错角相等,
,故本选项错误,不符合题意;
、,同位角相等,
,故本选项错误,不符合题意;
、,同旁内角互补,
,故本选项错误,不符合题意;
、,它们不是内错角或同位角,
与的关系无法判定,故本选项正确,符合题意.
故选:D.
7.D
解:①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
8.A
解:A选项:当∠1=∠A时,可知是DE和AC被AB所截得到的同位角,可得到DE∥AC,而不是AB∥DF,故符合题意;
B选项:当∠A=∠3时,可知是AB、DF被AC所截得到的同位角,可得AB∥DF,故不符合题意;
C选项:当∠1=∠4时,可知是AB、DF被DE所截得到的内错角,可得AB∥DF,故不符合题意;
D选项:当∠2+∠A=180°时,是一对同旁内角,可得AB∥DF;故不符合题意;
故选A.
9.D
解:根据内错角相等,两直线平行,
∵∠A=∠2,
∴AB∥CD,
故选:D.
10.A
解:由图形得,有两个相等的同位角,所以依据为:同位角相等,两直线平行.
故选:A.
11.B
解:A.如图,由内错角相等可知,第二次拐弯后与原来平行,但方向相反,故不符合题意;
B.如图,由同位角相等可知,第二次拐弯后与原来平行,且方向相同,故符合题意;
C.如图,由内错角不相等可知,第二次拐弯后与原来不平行,故不符合题意;
D.如图,由同位角不相等可知,第二次拐弯后与原来不平行,故不符合题意.
故选:B.
12.ACD
解:A、∵,∴,内错角相等,两直线平行,符合题意;
B、,无法判定,不符合题意;
C、∵∠4=∠5,∴,同位角相等,两直线平行,符合题意;
D、∵,∴,同旁内角互补,两直线平行,符合题意;
故选ACD
13.ABC
解:A、∠1=∠2,因为它们不是,被截得的同位角或内错角,符合题意;
B、∠2=∠4,因为它们不是,被截得的同位角或内错角,符合题意;
C、∠3=∠4,因为它们不是,被截得的同位角或内错角,符合题意;
D、∠1+∠4=180°,∠1的对顶角与∠4是,被截得的同旁内角,能推理得到,不符合题意.
故选:ABC.
14.ACD
解:A∵∠4=∠5,
∴l1∥l2,故本条件符合题意;
B由∠2+∠5=180°不能得到l1∥l2,故本条件符合题意;
C∵∠1=∠3,
∴l1∥l2,故本条件符合题意;
D∵∠6=∠2+∠3=∠1+∠2,
∴∠1=∠3,
∴l1∥l2,故本条件符合题意.
故选ACD.
15.内错角相等,两直线平行
解:由作图可知,
,
(内错角相等两直线平行),
故答案为:内错角相等,两直线平行.
16. 内错角相等,两直线平行
解:一副三角板如图摆放,
∴,
∴(内错角相等,两直线平行),
故答案为:;;内错角相等,两直线平行.
17. 同位角相等,两直线平行 垂直于同一直线的两条直线互相平行
解:,
,(同位角相等,两直线平行)
由此得出推论:
在同一平面内,垂直于同一直线的两条直线互相平行,
几何语言表述为:
,
∴,
故答案为:同位角相等,两直线平行;垂直于同一直线的两条直线互相平行;.
18.对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
解:证明:∵∠1+∠2=180°(已知),∠AEG=∠1(对顶角相等)
∴∠AEG+∠2=180°,
∴ABCD(同旁内角互补,两直线平行),
∴∠AEG=∠EGD(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠EGD(等式性质),
即∠FEG=∠EGH
∴EFGH(内错角相等,两直线平行)
故答案为:对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
19.见解析
解:证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
20.证明见解析.
解:
∵OF平分∠EOD (已知)
∴∠EOD =2∠FOD(角平分线的性质)
又∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠AGE=130°(已知)
∴∠AGO=50°(平角的定义)
∴∠EOD=∠AGO
∴AB//CD(内错角相等,两直线平行)
21.AD∥BC,理由见解析.
解:AD∥BC,理由如下:
∵∠ADE=∠DEF,∠EFC+∠C=180°,
∴AD∥EF,EF∥BC,
∴AD∥BC.
22.(1)见解析;(2),理由见解析.
解:(1)∵BE平分,平分,
∴,,
∵∠ABC=∠ADC ,
∴∠2=∠CDF,
∵∠1=∠2 ,
∴∠1=∠CDF,,
∴AB∥CD;
(2)AD∥BC,理由如下:
∵AB∥CD,
∴,
∵∠ABC=∠ADC ,
∴∠ADC+∠C=180°,
∴AD∥BC
答案第1页,共2页
