2021-2022学年人教版数学七年级下册5.3.1平行线的性质课后培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.3.1平行线的性质课后培优(Word版含答案) | 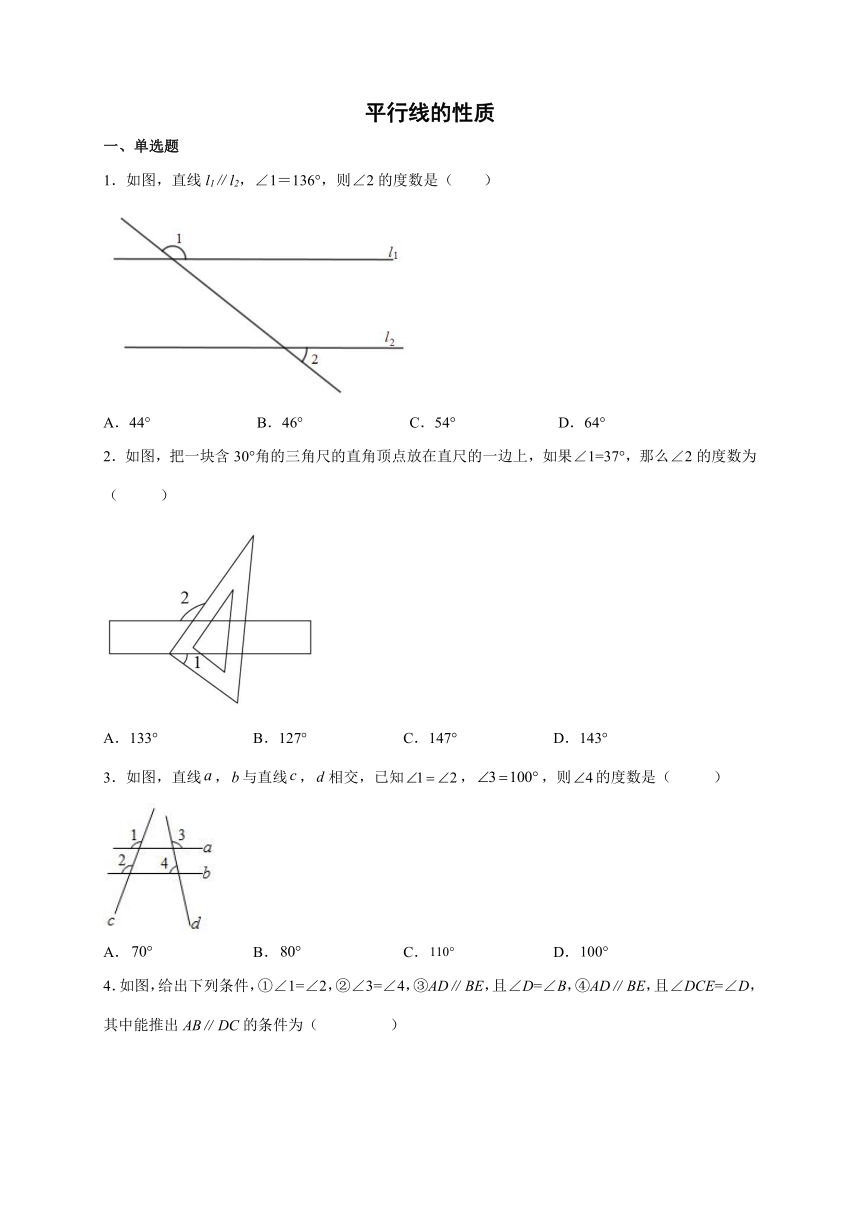 | |
| 格式 | docx | ||
| 文件大小 | 490.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 13:47:46 | ||
图片预览





文档简介
平行线的性质
一、单选题
1.如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A.44° B.46° C.54° D.64°
2.如图,把一块含30°角的三角尺的直角顶点放在直尺的一边上,如果∠1=37°,那么∠2的度数为( )
A.133° B.127° C.147° D.143°
3.如图,直线,与直线,相交,已知,,则的度数是( )
A. B. C. D.
4.如图,给出下列条件,①∠1=∠2,②∠3=∠4,③ADBE,且∠D=∠B,④ADBE,且∠DCE=∠D,其中能推出ABDC的条件为( )
A.①② B.②③ C.③④ D.②③④
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向右拐 50° ,第二次向左拐130° B.第一次向右拐 50° ,第二次向右拐130°
C.第一次向左拐 50° ,第二次向左拐130° D.第一次向左拐 30° ,第二次向右拐 30°
6.如图,将木条a,b与c钉在一起,∠1=100°,∠2=60°.要使木条a与b平行,木条a顺时针旋转的度数至少是( )
A.10° B.20° C.30° D.40°
7.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于( )
A.60° B.50° C.45° D.30°
8.如图,某位同学将一副三角板随意摆放在桌上,则图中的度数是( )
A.70° B.80° C.90° D.100°
9.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
10.已知直线,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.55° B.45° C.30° D.25°
二、多选题
11.下列说法中,是平行线判定的是( )
A.两条直线平行, 同旁内角互补 B.同位角相等, 两条直线平行
C.内错角相等, 两条直线平行 D.垂直于同一条直线的两条直线平行
12.如图,已知,不能判断的条件是( )
A. B. C. D.
13.如图,如果,,则下列结论正确的为( )
A. B. C.平分 D.
14.如图,AB∥EF∥DC,EG∥BD, 则图中与∠1相等的角有( )
A.∠DHE B.∠DBA C.∠CDB D.∠DEF
三、填空题
15.如图,已知AE∥BC,∠BAC=105°,∠DAE=48°,则∠C=______.
16.如图,∠C=90°,∠CAB=30°,AD∥BE,∠DAE=120°.给出以下结论:①∠2=∠EAB;②CA平分∠DAB;③∠1+∠2=90°;④BC∥AE.其中正确的结论有______.(写出所有正确结论的序号)
17.如图,若,,,那么_____.(用、表示)
18.如图,若∠1+∠2=180°,∠3=70°,则∠4=_______.
19.如图,AB∥CD,M在AB上,N在CD上,求∠1+∠2+∠3+∠4=_______.
四、解答题
20.完成下面的证明,
已知:如图,,CD、EF分别是、的平分线.
求证:.
证明:∵(______________)
∴______________(______________)
∴______________(______________)
∵、分别是、的平分线(______________)
∴,______________(______________)
∴(______________)
∴(______________)
21.如图,已知AB∥CD,∠A=60°,∠ECD=120°,求∠ECA的度数.
22.如图,平分交于点E,且.
(1)求证:;
(2)设点F为线段上一动点,连接.试判断这三个角的度数的和是否为某一固定值;若是,试求出这一固定值;若不是,请说明理由.
23.如图,直线EF分别与直线AB,CD相交于点A,C,AD平分∠BAC,交CD于点D,若∠1=∠2,且∠ADC=54°.
(1)直线AB、CD平行吗?为什么?
(2)求∠1的度数.
24.如图,已知于点F,于点D,,求证.
试卷第1页,共3页
参考答案:
1.A
解:∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
2.B
解:
,三角形为直角三角形
直尺上下两条线平行
故选B
3.B
解:如图,
,
,
,
则的度数是.
故选:B.
4.B
解:①∠1=∠2,
②∠3=∠4,
③ADBE,
∠D=∠B,
④∠DCE=∠D,
能推出ABDC的条件为②③
故选B
5.D
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D
6.B
解:如图,当时,∠2+∠3=180°
∵∠2=60°
∴∠3=120°
∵∠1=∠3
∴∠1=120°
∵现在木条a与木条c的夹角∠1=100°
∴木条a顺时针旋转的度数至少是120°﹣100°=20°
故选:B.
7.A
解:略
8.C
解:如图,过点作,
,
,
,
,
故选:C.
9.D
解:如图1,
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°,
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故选:D.
10.A
解:,,
,
直线,
,
故选:A.
11.BCD
解:A.两条直线平行, 同旁内角互补,是性质,不符合题意;
B.同位角相等, 两条直线平行,是判定定理,符合题意;
C.内错角相等, 两条直线平行,是判定定理,符合题意;
D.垂直于同一条直线的两条直线平行,是判定,符合题意;
故选:BCD.
12.ABD
解:能判断BECF的条件是∠1=∠4,理由:
∵ABCD,
∴∠CBA=∠BCD,
而∠1=∠4,
∴∠CBA ∠1=∠BCD ∠4,
即∠2=∠3,
∴BECF.
其中、、均不能判断
故选:ABD.
13.ABD
解:∵DE∥BC,
∴∠DCB=∠1,∠AED=∠ACB,故B符合题意;
∵∠1=∠2,
∴∠2=∠DCB,
∴FG∥DC,故A符合题意;
∴∠BFG=∠BDC,
又∵∠BDC+∠ADC=180°,
∴∠BFG+∠ADC=180°,故D符合题意;
∵∠BCD≠∠ACD,
∴CD平分∠ACB是错误的,故C不符合题意;
故选ABD.
14.ABC
解:∵AB∥EF∥DC,EG∥BD,
∴∠1=∠DBA(两直线平行,同位角相等),
∠DBA=∠DHE(两直线平行,同位角相等),
∠DBA=∠CDB(两直线平行,内错角相等),
∠DEF=∠A(两直线平行,同位角相等),
∴∠1=∠DHE=∠DBA=∠CDB,
故选:ABC.
15.27°
解:∵∠BAC=105°,∠DAE=48°,
∴∠EAC=180°-∠BAC-∠DAE=27°,
∵,
∴∠C=∠EAC=27°,
故答案为:27°.
16.①③##③①
解:∵∠BAC=30°,∠C=90°,
∴∠ABC=60°,
∴∠ABE+∠2=180°-∠ABC=180°-60°=120°,
∵AD∥BE,
∴∠ABE=∠BAD,
∵∠DAE=120°,
∴∠BAD+∠EAB=120°,即∠ABE+∠EAB=120°,
∴∠2=∠EAB,故①正确,符合题意;
∵∠BAC=30°,∠DAE=120°,
∴∠EAB+∠1=90°,
∵∠EAB=∠2,
∴∠1+∠2=90°,故③正确,符合题意;
∵∠1+∠EAB=90°,
∴∠1=90°-∠EAB,
∴∠1的大小随∠EAB的大小变化而变化,
∵∠EAB的度数不固定,
∴∠1=30°不一定成立,即∠1=∠BAC不一定成立,
∴AC不一定平分∠DAB,故②错误,不符合题意;
同理可知,∠2=60°不一定成立,
∴BC∥AE不一定成立,故④错误,不符合题意.
故答案为:①③.
17.
解:过点作,
,
,
,
,
故答案为:.
18.
解:如图,,
,
,
,
,
故答案为:.
19.540°
解:如图,过点E、F作EG、FH平行于AB,
∵AB∥CD,
∵AB∥EG∥FH∥CD,
∴∠1+∠MEG=180°,∠GEF+∠EFH=180°,∠HFN+∠4=180°,
∴∠1+∠MEF+∠EFN+∠4=540°,
故答案为:540°.
20.已知;DC;内错角相等,两直线平行;∠4;两直线平行,同位角相等;已知;2∠4;角平分线的定义;等量代换;同位角相等,两直线平行
解:∵(已知)
∴DC(内错角相等,两直线平行)
∴4(两直线平行,同位角相等)
∵、分别是、的平分线(已知)
∴,2∠4(角平分线的定义)
∴(等量代换)
∴(同位角相等,两直线平行).
21.∠ECA的度数为120°.
解:∵AB∥CD,∠A=60°,
∴∠A+∠ACD=180°,
∴∠ACD=120°,
∵∠ECD=120°,
∴∠ECA=360°-∠ECD-∠ACD=360°-120°-120°=120°,
故∠ECA的度数为120°.
22.(1)证明见解析
(2)是固定值;;理由见解析
解:∵,,
∴,
∴,
∵,
∴,
∴.
∴.
答案第1页,共2页
一、单选题
1.如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A.44° B.46° C.54° D.64°
2.如图,把一块含30°角的三角尺的直角顶点放在直尺的一边上,如果∠1=37°,那么∠2的度数为( )
A.133° B.127° C.147° D.143°
3.如图,直线,与直线,相交,已知,,则的度数是( )
A. B. C. D.
4.如图,给出下列条件,①∠1=∠2,②∠3=∠4,③ADBE,且∠D=∠B,④ADBE,且∠DCE=∠D,其中能推出ABDC的条件为( )
A.①② B.②③ C.③④ D.②③④
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向右拐 50° ,第二次向左拐130° B.第一次向右拐 50° ,第二次向右拐130°
C.第一次向左拐 50° ,第二次向左拐130° D.第一次向左拐 30° ,第二次向右拐 30°
6.如图,将木条a,b与c钉在一起,∠1=100°,∠2=60°.要使木条a与b平行,木条a顺时针旋转的度数至少是( )
A.10° B.20° C.30° D.40°
7.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于( )
A.60° B.50° C.45° D.30°
8.如图,某位同学将一副三角板随意摆放在桌上,则图中的度数是( )
A.70° B.80° C.90° D.100°
9.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
10.已知直线,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.55° B.45° C.30° D.25°
二、多选题
11.下列说法中,是平行线判定的是( )
A.两条直线平行, 同旁内角互补 B.同位角相等, 两条直线平行
C.内错角相等, 两条直线平行 D.垂直于同一条直线的两条直线平行
12.如图,已知,不能判断的条件是( )
A. B. C. D.
13.如图,如果,,则下列结论正确的为( )
A. B. C.平分 D.
14.如图,AB∥EF∥DC,EG∥BD, 则图中与∠1相等的角有( )
A.∠DHE B.∠DBA C.∠CDB D.∠DEF
三、填空题
15.如图,已知AE∥BC,∠BAC=105°,∠DAE=48°,则∠C=______.
16.如图,∠C=90°,∠CAB=30°,AD∥BE,∠DAE=120°.给出以下结论:①∠2=∠EAB;②CA平分∠DAB;③∠1+∠2=90°;④BC∥AE.其中正确的结论有______.(写出所有正确结论的序号)
17.如图,若,,,那么_____.(用、表示)
18.如图,若∠1+∠2=180°,∠3=70°,则∠4=_______.
19.如图,AB∥CD,M在AB上,N在CD上,求∠1+∠2+∠3+∠4=_______.
四、解答题
20.完成下面的证明,
已知:如图,,CD、EF分别是、的平分线.
求证:.
证明:∵(______________)
∴______________(______________)
∴______________(______________)
∵、分别是、的平分线(______________)
∴,______________(______________)
∴(______________)
∴(______________)
21.如图,已知AB∥CD,∠A=60°,∠ECD=120°,求∠ECA的度数.
22.如图,平分交于点E,且.
(1)求证:;
(2)设点F为线段上一动点,连接.试判断这三个角的度数的和是否为某一固定值;若是,试求出这一固定值;若不是,请说明理由.
23.如图,直线EF分别与直线AB,CD相交于点A,C,AD平分∠BAC,交CD于点D,若∠1=∠2,且∠ADC=54°.
(1)直线AB、CD平行吗?为什么?
(2)求∠1的度数.
24.如图,已知于点F,于点D,,求证.
试卷第1页,共3页
参考答案:
1.A
解:∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
2.B
解:
,三角形为直角三角形
直尺上下两条线平行
故选B
3.B
解:如图,
,
,
,
则的度数是.
故选:B.
4.B
解:①∠1=∠2,
②∠3=∠4,
③ADBE,
∠D=∠B,
④∠DCE=∠D,
能推出ABDC的条件为②③
故选B
5.D
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D
6.B
解:如图,当时,∠2+∠3=180°
∵∠2=60°
∴∠3=120°
∵∠1=∠3
∴∠1=120°
∵现在木条a与木条c的夹角∠1=100°
∴木条a顺时针旋转的度数至少是120°﹣100°=20°
故选:B.
7.A
解:略
8.C
解:如图,过点作,
,
,
,
,
故选:C.
9.D
解:如图1,
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°,
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故选:D.
10.A
解:,,
,
直线,
,
故选:A.
11.BCD
解:A.两条直线平行, 同旁内角互补,是性质,不符合题意;
B.同位角相等, 两条直线平行,是判定定理,符合题意;
C.内错角相等, 两条直线平行,是判定定理,符合题意;
D.垂直于同一条直线的两条直线平行,是判定,符合题意;
故选:BCD.
12.ABD
解:能判断BECF的条件是∠1=∠4,理由:
∵ABCD,
∴∠CBA=∠BCD,
而∠1=∠4,
∴∠CBA ∠1=∠BCD ∠4,
即∠2=∠3,
∴BECF.
其中、、均不能判断
故选:ABD.
13.ABD
解:∵DE∥BC,
∴∠DCB=∠1,∠AED=∠ACB,故B符合题意;
∵∠1=∠2,
∴∠2=∠DCB,
∴FG∥DC,故A符合题意;
∴∠BFG=∠BDC,
又∵∠BDC+∠ADC=180°,
∴∠BFG+∠ADC=180°,故D符合题意;
∵∠BCD≠∠ACD,
∴CD平分∠ACB是错误的,故C不符合题意;
故选ABD.
14.ABC
解:∵AB∥EF∥DC,EG∥BD,
∴∠1=∠DBA(两直线平行,同位角相等),
∠DBA=∠DHE(两直线平行,同位角相等),
∠DBA=∠CDB(两直线平行,内错角相等),
∠DEF=∠A(两直线平行,同位角相等),
∴∠1=∠DHE=∠DBA=∠CDB,
故选:ABC.
15.27°
解:∵∠BAC=105°,∠DAE=48°,
∴∠EAC=180°-∠BAC-∠DAE=27°,
∵,
∴∠C=∠EAC=27°,
故答案为:27°.
16.①③##③①
解:∵∠BAC=30°,∠C=90°,
∴∠ABC=60°,
∴∠ABE+∠2=180°-∠ABC=180°-60°=120°,
∵AD∥BE,
∴∠ABE=∠BAD,
∵∠DAE=120°,
∴∠BAD+∠EAB=120°,即∠ABE+∠EAB=120°,
∴∠2=∠EAB,故①正确,符合题意;
∵∠BAC=30°,∠DAE=120°,
∴∠EAB+∠1=90°,
∵∠EAB=∠2,
∴∠1+∠2=90°,故③正确,符合题意;
∵∠1+∠EAB=90°,
∴∠1=90°-∠EAB,
∴∠1的大小随∠EAB的大小变化而变化,
∵∠EAB的度数不固定,
∴∠1=30°不一定成立,即∠1=∠BAC不一定成立,
∴AC不一定平分∠DAB,故②错误,不符合题意;
同理可知,∠2=60°不一定成立,
∴BC∥AE不一定成立,故④错误,不符合题意.
故答案为:①③.
17.
解:过点作,
,
,
,
,
故答案为:.
18.
解:如图,,
,
,
,
,
故答案为:.
19.540°
解:如图,过点E、F作EG、FH平行于AB,
∵AB∥CD,
∵AB∥EG∥FH∥CD,
∴∠1+∠MEG=180°,∠GEF+∠EFH=180°,∠HFN+∠4=180°,
∴∠1+∠MEF+∠EFN+∠4=540°,
故答案为:540°.
20.已知;DC;内错角相等,两直线平行;∠4;两直线平行,同位角相等;已知;2∠4;角平分线的定义;等量代换;同位角相等,两直线平行
解:∵(已知)
∴DC(内错角相等,两直线平行)
∴4(两直线平行,同位角相等)
∵、分别是、的平分线(已知)
∴,2∠4(角平分线的定义)
∴(等量代换)
∴(同位角相等,两直线平行).
21.∠ECA的度数为120°.
解:∵AB∥CD,∠A=60°,
∴∠A+∠ACD=180°,
∴∠ACD=120°,
∵∠ECD=120°,
∴∠ECA=360°-∠ECD-∠ACD=360°-120°-120°=120°,
故∠ECA的度数为120°.
22.(1)证明见解析
(2)是固定值;;理由见解析
解:∵,,
∴,
∴,
∵,
∴,
∴.
∴.
答案第1页,共2页
