2021—2022学年苏科版数学八年级下册9.1~9.3阶段复习提升练(旋转、中心对称、平行四边形)(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.1~9.3阶段复习提升练(旋转、中心对称、平行四边形)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 421.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 14:10:16 | ||
图片预览



文档简介
9.1~9.3 阶段复习提升练(旋转、中心对称、平行四边形)
-2021-2022学年八年级数学下册(苏科版)
一、选择题
1、(2020春 西湖区校级期中)下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
2、(2020·苏州·中考真题)如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为( )
A. B. C. D.
(2题) (5题) (6题)
3、(2020春 罗山县期末)已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
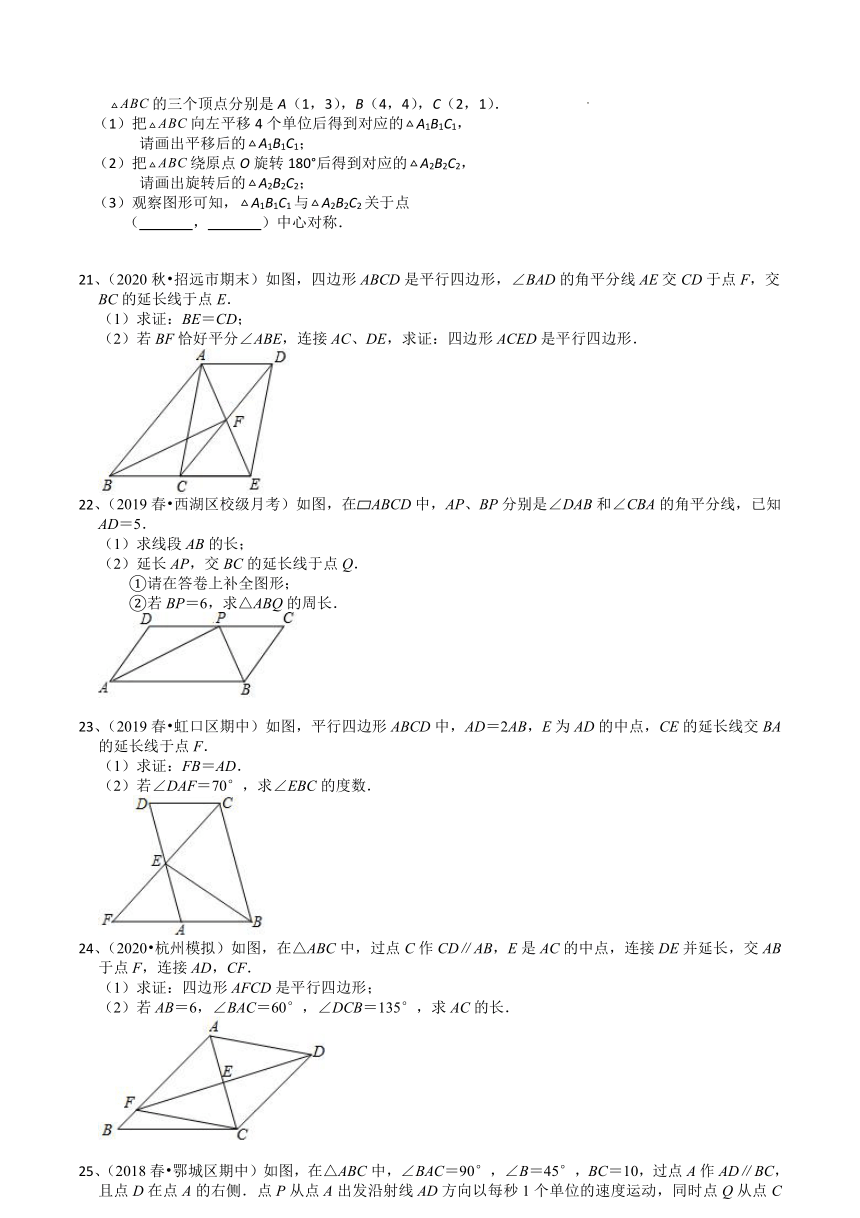
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;
③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
4、(2020秋 新华区校级月考)用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
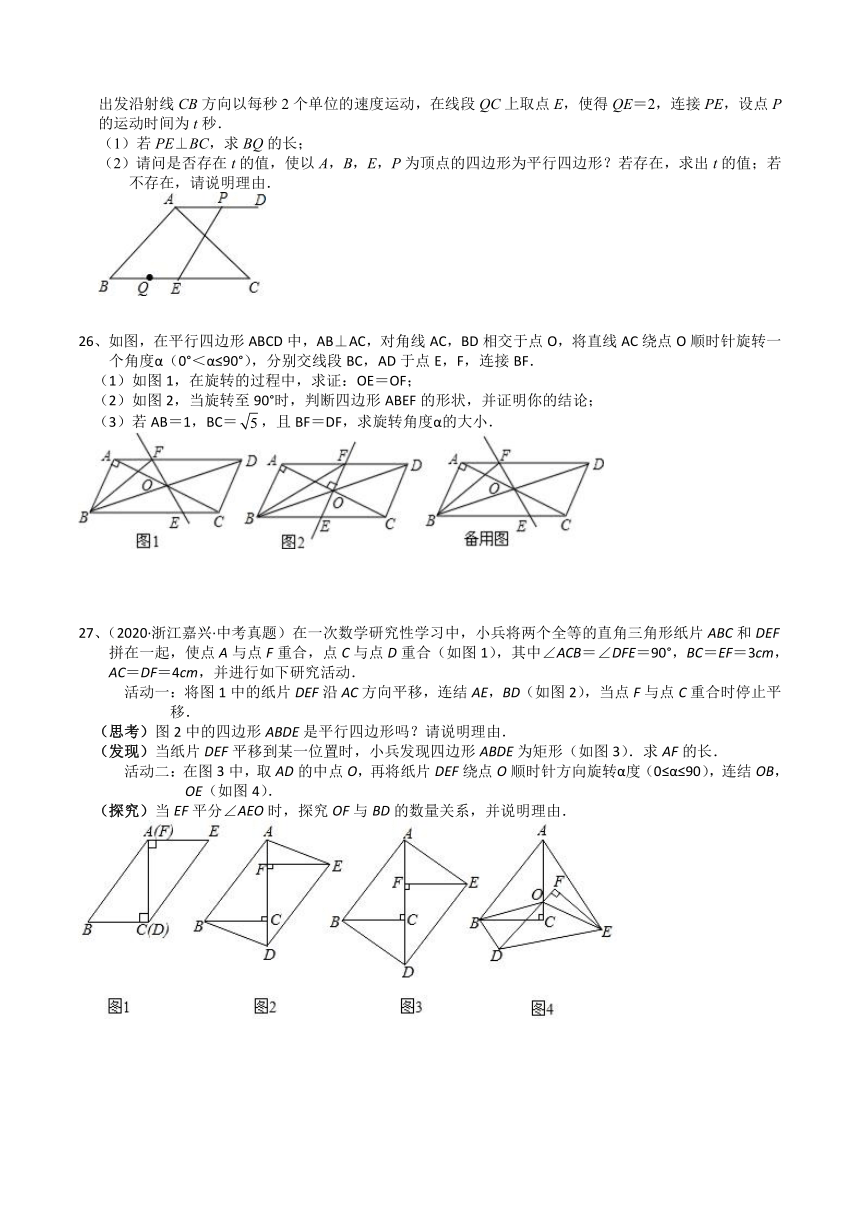
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
5、(2021春 沙坪坝区校级月考)如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使四边形AECF是平行四边形,则添加的条件不能是( )
A.AE=CF B.BE=FD C.BF=DE D.∠1=∠2
6、(2020春 萧山区期末)如图,在 ABCD中,E是CD上一点,BE=BC.若∠A:∠ADC=1:2,则∠ABE的度数是( )
A.70° B.65° C.60° D.55°
7、(2020 贵阳模拟)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是 .
(7题) (8题)
8、(2020春 青川县期末)如图,平行四边形ABCD中,AC和BD交于点O,若AC=8,BD=6,则边AD长的取值范围是( )
A.1<AD<7 B.5<AD<11 C.6<AD<8 D.3<AD<4
9、(2020春 沙坪坝区期末)平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cm
A.14 B.16 C.12或14 D.14或16
10、如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
(10题) (11题) (12题)
二、填空题
11、如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,
则____________
12、如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
13、(2021·山东枣庄·中考真题)如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为_______.
(13题) (15题) (16题)
14、(2020春 临邑县期末)平行四边形ABCD的对角线AC,BD交于点O,△OAB的周长比△BOC的周长小3cm,若AB=5cm,则平行四边形ABCD的周长是 cm.
15、(2020春 仙居县期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,若AB=5,AD=3,则BD的长为 .
16、(2020 长春模拟)如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
17、(2019秋 江北区校级期末)如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
(17题) (18题)
18、(2020 江西模拟)如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为 .
三、解答题
19、(2020 衢州模拟)如图,在 ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
20、(2020·广西中考真题)如图,在平面直角坐标系中,
的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把向左平移4个单位后得到对应的A1B1C1,
请画出平移后的A1B1C1;
(2)把绕原点O旋转180°后得到对应的A2B2C2,
请画出旋转后的A2B2C2;
(3)观察图形可知,A1B1C1与A2B2C2关于点
( , )中心对称.
21、(2020秋 招远市期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
22、(2019春 西湖区校级月考)如图,在 ABCD中,AP、BP分别是∠DAB和∠CBA的角平分线,已知AD=5.
(1)求线段AB的长;
(2)延长AP,交BC的延长线于点Q.
①请在答卷上补全图形;
②若BP=6,求△ABQ的周长.
23、(2019春 虹口区期中)如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
24、(2020 杭州模拟)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
25、(2018春 鄂城区期中)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
26、如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=,且BF=DF,求旋转角度α的大小.
27、(2020·浙江嘉兴·中考真题)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.
(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
9.1~9.3 阶段复习提升练(旋转、中心对称、平行四边形)
-2021-2022学年八年级数学下册(苏科版)(解析)
一、选择题
1、(2020春 西湖区校级期中)下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
【点拨】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.
【解析】解:根据中心对称图形的定义可知从左到右第1个图形和第三个图形是中心对称图形,第二和第四个图形不是中心对称图形.
故选:C.
2、(2020·苏州·中考真题)如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为( )
A. B. C. D.
【分析】本题考查了三角形内角和定理,旋转的性质的应用及等腰三角形得性质.
根据旋转的性质得出边和角相等,找到角之间的关系,再根据三角形内角和定理进行求解,即可求出答案.
【详解】
解:设=x°.
根据旋转的性质,得∠C=∠= x°,=AC, =AB. ∴∠=∠B.
∵,∴∠C=∠CA=x°. ∴∠=∠C+∠CA=2x°. ∴∠B=2x°.
∵∠C+∠B+∠CAB=180°,,
∴x+2x+108=180. 解得x=24. ∴的度数为24°.
故选:C.
3、(2020春 罗山县期末)已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;
③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
【点拨】平行四边形的判定方法共有五种,在四边形中如果有:1、四边形的两组对边分别平行;
2、一组对边平行且相等;3、两组对边分别相等;4、对角线互相平分;
5、两组对角分别相等.则四边形是平行四边形.
根据已知,结合题意,画出图形,再根据平行四边形的判定,逐一判断即可.
【解析】解:①也可能是等腰梯形.
②可得AD∥BC,故正确.
③可判定△ABO≌△CDO,就有AB=CD,故可判定为平行四边形,正确.
④也可能是等腰梯形.
故选:C.
4、(2020秋 新华区校级月考)用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
【点拨】本题考查的是反证法的应用,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解析】解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
5、(2021春 沙坪坝区校级月考)如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使四边形AECF是平行四边形,则添加的条件不能是( )
A.AE=CF B.BE=FD C.BF=DE D.∠1=∠2
【点拨】可以针对平行四边形的各种判定方法,给出条件.答案可以有多种,主要条件明确,说法有理即可.
【解析】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠ABD=∠CDB;
又∵BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE;∴AE∥CF;
∴四边形AECF是平行四边形,故B正确;
∵四边形ABCD是平行四边形,∴AB=CD,∠ABD=∠CDB;
又∵BF=DE,∴BF﹣EF=DE﹣EF,∴BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD;∴∠AEF=∠CFE;∴AE∥CF;
∴四边形AECF是平行四边形,故C正确;
∵四边形ABCD是平行四边形,∴AB=CD,∠ABD=∠CDB;
又∵∠1=∠2,∴△ABE≌△CDF(ASA),∴AE=CF,∠AEB=∠CFD;
∴∠AEF=∠CFE;∴AE∥CF;∴四边形AECF是平行四边形,故D正确;
添加AE=CF后,不能得出△ABE≌△CDF,进而得不出四边形AECF是平行四边形,
故选:A.
6、(2020春 萧山区期末)如图,在 ABCD中,E是CD上一点,BE=BC.若∠A:∠ADC=1:2,则∠ABE的度数是( )
A.70° B.65° C.60° D.55°
【点拨】根据平行四边形的性质和∠A:∠ADC=1:2,可以得到∠A的度数,从而可以得到∠C的度数,然后根据BE=BC,可以判断△BCE的形状,再根据平行线的性质,可以得到∠ABE和∠BEC的关系,从而可以得到∠ABE的度数.
【解析】解:∵四边形ABCD是平行四边形,∴∠A+∠ADC=180°,∠A=∠C,
∵∠A:∠ADC=1:2,
∴∠A=60°,∠ADC=120°,∴∠C=60°,
∵BE=BC,∴△BCE是等边三角形,∴∠BEC=60°,
∵DC∥AB,∴∠BEC=∠ABE,∴∠ABE=60°,
故选:C.
7、(2020 贵阳模拟)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是 .
【点拨】直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【解析】解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长=AO+OB+AB=8+6=14.
故答案为:14.
8、(2020春 青川县期末)如图,平行四边形ABCD中,AC和BD交于点O,若AC=8,BD=6,则边AD长的取值范围是( )
A.1<AD<7 B.5<AD<11 C.6<AD<8 D.3<AD<4
【点拨】根据平行四边形对角线互相平分可得AO=4,DO=3,再根据三角形的三边关系可得4﹣3<AD<4+3,再解即可.
【解析】解:∵四边形ABCD是平行四边形,
∴AO=AC,DO=BD,
∵AC=8,BD=6,
∴AO=4,DO=3,
∴4﹣3<AD<4+3,
解得:1<AD<7,
故选:A.
9、(2020春 沙坪坝区期末)平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cm
A.14 B.16 C.12或14 D.14或16
【点拨】根据题意画出图形,由平行四边形得出对边平行,又由角平分线可以得出△ABE为等腰三角形,然后分别讨论BE=2cm,CE=3cm或BE=3cm,CE=2cm,继而求得答案.
【解析】解:如图,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DAE=∠AEB,
∵AE为角平分线,∴∠DAE=∠BAE,∴∠AEB=∠BAE,∴AB=BE,
∴①当AB=BE=2cm,CE=3cm时,BC=BE+CE=5cm,
则平行四边形的周长=2(2+5)=14(cm);
②当AB=BE=3cm时,CE=2cm,BC=BE+CE=5cm,
则平行四边形的周长=2(3+5)=16(cm);
故选:D.
10、如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
【分析】本题考查的是平行四边形的判定和性质、等边三角形的性质以及三角形面积等知识,熟练掌握平行四边形的判定与性质和等边三角形的性质,证明四边形BCDF为平行四边形是解题关键.
由平行四边形的判定定理判断②,再由平行四边形的性质和平行线的性质判断①,然后由三角形三边关系判断③,最后由等边三角形的性质分别求出△ACD、△ACB、△ABE的面积,计算即可判断④.
【详解】
解:∵∠ACB=90°,∠ABC=30°,,
∵△ACD是等边三角形,∴∠ACD=60°,
∴∠ACD=∠BAC,∴CD∥AB,
∵F为AB的中点,∴BF=AB,
∴BF∥AB,CD=BF,∴四边形BCDF为平行四边形,故②正确;
∵四边形BCDF为平行四边形,∴DF∥BC,
又∵∠ACB=90°,∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,∴DA+DF>BE,故③错误;
设AC=x,则AB=2x,,
,故④正确;
故选:D.
二、填空题
11、如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,
则____________
【分析】此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ADF与△CBE是等腰三角形是关键.
由平行四边形ABCD中,∠ADC,∠BCD的平分线分别交AB于点F、E,易证得△ADF与△CBE是等腰三角形,又由AB=5,BC=3,即可求得答案.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=5,AD=BC=3,
∴∠AFD=∠CDF,∠DCE=∠BEC,
∵∠ADC,∠BCD的平分线分别交AB于点F、E,
∴∠ADF=∠CDF,∠BCE=∠DCE,
∴∠AFD=∠ADF,∠BCE=∠BEC,
∴AF=AD=3,BC=BE=3,
∴EF=AF+BE-AB=3+3-5=1.
故答案为1.
12、如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
【分析】此题考查平行四边形的性质,全等三角形的判定及性质,熟记全等三角形的判定是解题的关键.
证明△MOD≌△NOB,得到S△MOD=S△NOB,利用平行四边形的性质得到S阴影=,由此求出答案.
【详解】
解:∵四边形ABCD是平行四边形,∴BC,OB=OD,∴∠MDO=∠NBO,
∵∠MOD=∠NOB,∴△MOD≌△NOB,∴S△MOD=S△NOB,
∴S阴影=,
故答案为:1.
13、(2021·山东枣庄·中考真题)如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为_______.
试题分析:坐标与图形变化-旋转
连接AA′、CC′,作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.∵直线MN为:x=1,设直线CC′为y=kx+b,
由题意:, ∴, ∴直线CC′为y=x+,
∵直线EF⊥CC′,经过CC′中点(,), ∴直线EF为y=﹣3x+2,
由得, ∴P(1,﹣1).
14、(2020春 临邑县期末)平行四边形ABCD的对角线AC,BD交于点O,△OAB的周长比△BOC的周长小3cm,若AB=5cm,则平行四边形ABCD的周长是 cm.
【点拨】根据平行四边形性质得出OA=OC,AB=CD,AD=BC,求出BC=8cm,即可得出平行四边形的周长.
【解析】解:∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC,
∵△OAB的周长比△OBC的周长小3cm,∴(BC+OC+OB)﹣(AB+OA+OB)=3cm,
∴BC﹣AB=3cm,∴BC=AB+3cm=8cm,
∴平行四边形ABCD的周长=2(AB+BC)=26cm;
故答案为:26.
15、(2020春 仙居县期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,若AB=5,AD=3,则BD的长为 .
【点拨】根据AC⊥BC,AB=5,AD=3,可以得到AC的长,再根据平行四边形的性质,可以得到DE和BE的长,然后根据勾股定理即可求得BD的长.
【解析】解:∵四边形ABCD是平行四边形,∴AD=BC,
∵AC⊥BC,AB=5,AD=3,∴∠ACB=90°,BC=3,∴AC=4,
作DE⊥BC交BC的延长线于点E,
∵AC⊥BC,∴AC∥DE,
又∵AD∥CE,∴四边形ACED是平行四边形,∴AC=DE,AD=CE,∴DE=4,BE=6,
∵∠DEB=90°,∴BD===2,
故答案为:2.
16、(2020 长春模拟)如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
【点拨】本题主要考查了平行四边形的性质,全等三角形的判定与性质以及等腰三角形的性质的综合运用,解决问题的关键是作辅助线构造全等三角形,利用全等三角形的对应边相等,对应角相等进行推算.
延长AE,BC交于点G,判定△ADE≌△GCE,即可得出CG=AD=5,AE=GE,再根据三线合一即可得到FE⊥AG,进而得出Rt△AEF中,EF=AF=4.
【解析】解:如图,延长AE,BC交于点G,
∵点E是CD的中点,∴DE=CE,
∵平行四边形ABCD中,AD∥BC,∴∠D=∠ECG,
又∵∠AED=∠GEC,∴△ADE≌△GCE,∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,∴AF=GF=3+5=8,
又∵E是AG的中点,∴FE⊥AG,∴Rt△AEF中,EF=AF=4,
故答案为:4.
17、(2019秋 江北区校级期末)如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
【点拨】本题考查了平行四边形的判定和性质的应用,题目是一道综合性比较强的题目,难度适中,解题的关键是把握“化动为静”的解题思想.
当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【解析】解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,∴PD=AD﹣AP=12﹣t,
∵AD∥BC,∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
18、(2020 江西模拟)如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为 .
【点拨】分两种情况:(1)当∠BPC=90°时,①由直角三角形的性质即可得出BP=2;
②当点P在边AD上,AP=DP=2时,由等边三角形的性质和勾股定理求出BP即可;
(2)当∠BCP=90°时,CP=PD=,由勾股定理求出BP即可.
【解析】解:分两种情况:
(1)当∠BPC=90°时,
①点P在AB边上时,∵∠B=60°,∴∠BCP=30°,∴BP=BC=2;
②点P在边AD上,AP=DP=2时,如图2所示:
∵四边形ABCD是平行四边形,∴CD=AB=2,∠D=∠B=60°,
∴DP=CD,∴△PCD是等边三角形,PC=CD=2,
∴BP===2;
(2)当∠BCP=90°时,如图3所示:则CPD=90°,
∵CD=AB=2,∠D=∠ABC=60°,∴∠PCD=30°,
∴PD=CD=1,CP=PD=,∴BP==;
综上所述:当△PBC为直角三角形时,BP的长为2或2或.
故答案为:2或2或.
三、解答题
19、(2020 衢州模拟)如图,在 ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
【点拨】本题中,在连接BD交AC于O,则可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
【解析】证明:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO
∵AE=CF,
∴AO﹣AE=CO﹣CF.
即EO=FO.
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形).
20、(2020·广西中考真题)如图,在平面直角坐标系中,的三个顶点分别是A(1,3),B(4,4),
C(2,1).
(1)把向左平移4个单位后得到对应的A1B1C1,请画出平移后的A1B1C1;
(2)把绕原点O旋转180°后得到对应的A2B2C2,请画出旋转后的A2B2C2;
(3)观察图形可知,A1B1C1与A2B2C2关于点( , )中心对称.
【分析】
(1)依据平移的方向和距离,即可得到平移后的△A1B1C1;
(2)依据△ABC绕原点O旋转180°,即可画出旋转后的△A2B2C2;
(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.
【详解】
解:(1)如图所示,分别确定平移后的对应点,
得到A1B1C1即为所求;
(2)如图所示,分别确定旋转后的对应点,
得到A2B2C2即为所求;
(3)由图可得,A1B1C1与A2B2C2关于点成中心对称.
故答案为:﹣2,0.
21、(2020秋 招远市期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
【点拨】本题考查了平行四边形的性质和判定,全等三角形的性质和判定,等腰三角形的判定和平行线的性质等知识点,能综合运用定理进行推理是解此题的关键.
(1)根据平行四边形的性质得出AD∥BC,AB=CD,根据平行线的性质得出∠DAE=∠AEB,求出∠BAE=∠AEB,根据等腰三角形的判定得出即可;
(2)根据等腰三角形的性质得出AF=EF,求出△ADF≌△ECF,根据全等三角形的性质得出DF=CF,再根据平行四边形的判定得出即可.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,
∴BE=AB,∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,∴AF=EF,
在△ADF和△ECF中,,∴△ADF≌△ECF(ASA),∴DF=CF,
又∵AF=EF,∴四边形ACED是平行四边形.
22、(2019春 西湖区校级月考)如图,在 ABCD中,AP、BP分别是∠DAB和∠CBA的角平分线,已知AD=5.
(1)求线段AB的长;
(2)延长AP,交BC的延长线于点Q.
①请在答卷上补全图形;
②若BP=6,求△ABQ的周长.
【点拨】(1)依据平行线的性质以及角平分线的定义即可得到DP=AD=5,CP=BC=5,进而得出AB的长;
(2)依据平行线的性质以及角平分线的定义即可得到AB=QB,再根据BP平分∠ABQ,即可得出BP⊥AQ,AP=QP,依据勾股定理得出AP的长,进而得到△ABQ的周长.
【解析】解:(1)∵在 ABCD中,AD=5,∴BC=5,
∵AB∥CD,∴∠BAP=∠DPA,
∵AP平分∠BAD,∴∠BAP=∠DAP,∴∠DAP=∠DPA,∴DP=AD=5,
同理可得,CP=BC=5,∴CD=10,∴AB=10;
(2)①如图所示:
②∵AD∥BQ,∴∠Q=∠DAP,
又∵∠DAP=∠BAP,∴∠Q=∠BAP,∴AB=QB=10,
又∵BP平分∠ABQ,∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP===8,
∴AQ=16,∴△ABQ的周长为:16+10+10=36.
23、(2019春 虹口区期中)如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
【点拨】(1)证△DEC≌△AEF(AAS),得出DC=FA,进而得出结论;
(2)由平行四边形的对边平行证出∠CBF=∠DAF=70°,∠AEB=∠EBC,由等腰三角形的性质得出∠AEB=∠ABE,即可得出答案.
【解析】(1)证明∵E为AD的中点,∴DE=AE,
∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC,∴∠EDC=∠EAF,
在△DEC和△AEF中,,∴△DEC≌△AEF(AAS),∴DC=FA,
∵AD=2AB,∴AB=DE=EA=FA,∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,∴∠AEB=∠ABE,∴∠EBC=∠ABE=35°.
24、(2020 杭州模拟)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
【点拨】(1)先证△AEF≌△CED(AAS),得AF=CD,再由CD∥AB,即AF∥CD,即可得出结论;
(2)过C作CM⊥AB于M,先证△BCM是等腰直角三角形,得BM=CM,再由含30°角的直角三角形的性质得AC=2AM,BM=CM=AM,由AM+BM=AB求出AM=3﹣3,即可求解.
【解析】(1)证明:∵E是AC的中点,∴AE=CE,
∵CD∥AB,∴∠AFE=∠CDE,
在△AEF和△CED中,,∴△AEF≌△CED(AAS),∴AF=CD,
又∵CD∥AB,即AF∥CD,∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:则∠CMB=∠CMA=90°,
∵CD∥AB,∴∠B+∠DCB=180°,∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,∴BM=CM,
∵∠BAC=60°,∴∠ACM=30°,∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,∴AM+AM=6,解得:AM=3﹣3,∴AC=2AM=6﹣6.
25、(2018春 鄂城区期中)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
【点拨】本题考查了平行四边形的判定、等腰直角三角形的判定与性质、等腰三角形的性质等知识;根据题意得出t的方程是解决问题的突破口.
(1)作AM⊥BC于M,由已知条件得出AB=AC,由等腰三角形的性质得出BM=CM,由直角三角形斜边上的中线性质得出AM=BC=5,证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5﹣t,由CE=CQ﹣QE=2t﹣2得出方程,解方程即可;
(2)由平行四边形的判定得出AP=BE,得出方程,解方程即可.
【解析】解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,
∴BM=CM,∴AM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10, 解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
26、如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=,且BF=DF,求旋转角度α的大小.
【分析】此题是四边形综合题,主要考查了平行四边形的性质和判定,全等三角形的判定和性质,等腰三角形的判定和性质,等腰直角三角形的性质,旋转的性质,判断出△ABO是等腰直角三角形是解本题的关键.
(1)由平行四边形的性质得出∠OAF=∠OCE,OA=OC,进而判断出△AOF≌△COE,即可得出结论;
(2)先判断出∠BAC=∠AOF,得出AB∥EF,即可得出结论;
(3)先求出AC=2,进而得出A=1=AB,即可判断出△ABO是等腰直角三角形,进一步判断出△BFD是等腰三角形,利用等腰三角形的三线合一得出∠BOF=90°,即可得出结论.
【详解】
(1)证明:在 ABCD中,AD∥BC,∴∠OAF=∠OCE,
∵OA=OC,∠AOF=∠COE,∴△AOF≌△COE(ASA),∴OE=OF;
(2)当旋转角为90°时,四边形ABEF是平行四边形,理由:
∵AB⊥AC,∴∠BAC=90°,
∵∠AOF=90°,∴∠BAC=∠AOF,∴AB∥EF,
∵AF∥BE,∴四边形ABEF是平行四边形;
(3)在Rt△ABC中,AB=1,BC=,∴AC==2,
∴OA=1=AB,∴△ABO是等腰直角三角形,∴∠AOB=45°,
∵BF=DF,∴△BFD是等腰三角形,
∵四边形ABCD是平行四边形,∴OB=OD,
∴OF⊥BD(等腰三角形底边上的中线是底边上的高),
∴∠BOF=90°,∴∠α=∠AOF=∠BOF﹣∠AOB=45°.
27、(2020·浙江嘉兴·中考真题)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.
(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
【答案】【思考】是,理由见解析;【发现】;【探究】BD=2OF,理由见解析;
【分析】本题考查了图形的综合变换,涉及了三角形全等的判定与性质、平行四边形的判定与性质等,准确识图,熟练掌握和灵活运用相关知识是解题的关键.
【思考】由全等三角形的性质得出AB=DE,∠BAC=∠EDF,则AB∥DE,可得出结论;
【发现】连接BE交AD于点O,设AF=x(cm),则OA=OE=(x+4),得出OF=OA﹣AF=2﹣x,由勾股定理可得,解方程求出x,则AF可求出;
【探究】如图2,延长OF交AE于点H,证明△EFO≌△EFH(ASA),得出EO=EH,FO=FH,则∠EHO=∠EOH=∠OBD=∠ODB,可证得△EOH≌△OBD(AAS),得出BD=OH,则结论得证.
【详解】
解:【思考】四边形ABDE是平行四边形.
证明:如图,∵△ABC≌△DEF,
∴AB=DE,∠BAC=∠EDF,∴AB∥DE,∴四边形ABDE是平行四边形;
【发现】
如图1,连接BE交AD于点O,
∵四边形ABDE为矩形,∴OA=OD=OB=OE,
设AF=x(cm),则OA=OE=(x+4),∴OF=OA﹣AF=2﹣x,
在Rt△OFE中,∵OF2+EF2=OE2,
∴,解得:x=,∴AF=cm.
【探究】BD=2OF,
证明:如图2,延长OF交AE于点H,
∵四边形ABDE为矩形,∴∠OAB=∠OBA=∠ODE=∠OED,OA=OB=OE=OD,
∴∠OBD=∠ODB,∠OAE=∠OEA,
∴∠ABD+∠BDE+∠DEA+∠EAB=360°,∴∠ABD+∠BAE=180°,
∴AE∥BD,∴∠OHE=∠ODB,
∵EF平分∠OEH,∴∠OEF=∠HEF,
∵∠EFO=∠EFH=90°,EF=EF,∴△EFO≌△EFH(ASA),∴EO=EH,FO=FH,
∴∠EHO=∠EOH=∠OBD=∠ODB,
∴△EOH≌△OBD(AAS),∴BD=OH=2OF.
-2021-2022学年八年级数学下册(苏科版)
一、选择题
1、(2020春 西湖区校级期中)下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
2、(2020·苏州·中考真题)如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为( )
A. B. C. D.
(2题) (5题) (6题)
3、(2020春 罗山县期末)已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;
③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
4、(2020秋 新华区校级月考)用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
5、(2021春 沙坪坝区校级月考)如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使四边形AECF是平行四边形,则添加的条件不能是( )
A.AE=CF B.BE=FD C.BF=DE D.∠1=∠2
6、(2020春 萧山区期末)如图,在 ABCD中,E是CD上一点,BE=BC.若∠A:∠ADC=1:2,则∠ABE的度数是( )
A.70° B.65° C.60° D.55°
7、(2020 贵阳模拟)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是 .
(7题) (8题)
8、(2020春 青川县期末)如图,平行四边形ABCD中,AC和BD交于点O,若AC=8,BD=6,则边AD长的取值范围是( )
A.1<AD<7 B.5<AD<11 C.6<AD<8 D.3<AD<4
9、(2020春 沙坪坝区期末)平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cm
A.14 B.16 C.12或14 D.14或16
10、如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
(10题) (11题) (12题)
二、填空题
11、如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,
则____________
12、如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
13、(2021·山东枣庄·中考真题)如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为_______.
(13题) (15题) (16题)
14、(2020春 临邑县期末)平行四边形ABCD的对角线AC,BD交于点O,△OAB的周长比△BOC的周长小3cm,若AB=5cm,则平行四边形ABCD的周长是 cm.
15、(2020春 仙居县期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,若AB=5,AD=3,则BD的长为 .
16、(2020 长春模拟)如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
17、(2019秋 江北区校级期末)如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
(17题) (18题)
18、(2020 江西模拟)如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为 .
三、解答题
19、(2020 衢州模拟)如图,在 ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
20、(2020·广西中考真题)如图,在平面直角坐标系中,
的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把向左平移4个单位后得到对应的A1B1C1,
请画出平移后的A1B1C1;
(2)把绕原点O旋转180°后得到对应的A2B2C2,
请画出旋转后的A2B2C2;
(3)观察图形可知,A1B1C1与A2B2C2关于点
( , )中心对称.
21、(2020秋 招远市期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
22、(2019春 西湖区校级月考)如图,在 ABCD中,AP、BP分别是∠DAB和∠CBA的角平分线,已知AD=5.
(1)求线段AB的长;
(2)延长AP,交BC的延长线于点Q.
①请在答卷上补全图形;
②若BP=6,求△ABQ的周长.
23、(2019春 虹口区期中)如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
24、(2020 杭州模拟)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
25、(2018春 鄂城区期中)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
26、如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=,且BF=DF,求旋转角度α的大小.
27、(2020·浙江嘉兴·中考真题)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.
(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
9.1~9.3 阶段复习提升练(旋转、中心对称、平行四边形)
-2021-2022学年八年级数学下册(苏科版)(解析)
一、选择题
1、(2020春 西湖区校级期中)下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
【点拨】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.
【解析】解:根据中心对称图形的定义可知从左到右第1个图形和第三个图形是中心对称图形,第二和第四个图形不是中心对称图形.
故选:C.
2、(2020·苏州·中考真题)如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为( )
A. B. C. D.
【分析】本题考查了三角形内角和定理,旋转的性质的应用及等腰三角形得性质.
根据旋转的性质得出边和角相等,找到角之间的关系,再根据三角形内角和定理进行求解,即可求出答案.
【详解】
解:设=x°.
根据旋转的性质,得∠C=∠= x°,=AC, =AB. ∴∠=∠B.
∵,∴∠C=∠CA=x°. ∴∠=∠C+∠CA=2x°. ∴∠B=2x°.
∵∠C+∠B+∠CAB=180°,,
∴x+2x+108=180. 解得x=24. ∴的度数为24°.
故选:C.
3、(2020春 罗山县期末)已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;
③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
【点拨】平行四边形的判定方法共有五种,在四边形中如果有:1、四边形的两组对边分别平行;
2、一组对边平行且相等;3、两组对边分别相等;4、对角线互相平分;
5、两组对角分别相等.则四边形是平行四边形.
根据已知,结合题意,画出图形,再根据平行四边形的判定,逐一判断即可.
【解析】解:①也可能是等腰梯形.
②可得AD∥BC,故正确.
③可判定△ABO≌△CDO,就有AB=CD,故可判定为平行四边形,正确.
④也可能是等腰梯形.
故选:C.
4、(2020秋 新华区校级月考)用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
【点拨】本题考查的是反证法的应用,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解析】解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
5、(2021春 沙坪坝区校级月考)如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使四边形AECF是平行四边形,则添加的条件不能是( )
A.AE=CF B.BE=FD C.BF=DE D.∠1=∠2
【点拨】可以针对平行四边形的各种判定方法,给出条件.答案可以有多种,主要条件明确,说法有理即可.
【解析】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠ABD=∠CDB;
又∵BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE;∴AE∥CF;
∴四边形AECF是平行四边形,故B正确;
∵四边形ABCD是平行四边形,∴AB=CD,∠ABD=∠CDB;
又∵BF=DE,∴BF﹣EF=DE﹣EF,∴BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD;∴∠AEF=∠CFE;∴AE∥CF;
∴四边形AECF是平行四边形,故C正确;
∵四边形ABCD是平行四边形,∴AB=CD,∠ABD=∠CDB;
又∵∠1=∠2,∴△ABE≌△CDF(ASA),∴AE=CF,∠AEB=∠CFD;
∴∠AEF=∠CFE;∴AE∥CF;∴四边形AECF是平行四边形,故D正确;
添加AE=CF后,不能得出△ABE≌△CDF,进而得不出四边形AECF是平行四边形,
故选:A.
6、(2020春 萧山区期末)如图,在 ABCD中,E是CD上一点,BE=BC.若∠A:∠ADC=1:2,则∠ABE的度数是( )
A.70° B.65° C.60° D.55°
【点拨】根据平行四边形的性质和∠A:∠ADC=1:2,可以得到∠A的度数,从而可以得到∠C的度数,然后根据BE=BC,可以判断△BCE的形状,再根据平行线的性质,可以得到∠ABE和∠BEC的关系,从而可以得到∠ABE的度数.
【解析】解:∵四边形ABCD是平行四边形,∴∠A+∠ADC=180°,∠A=∠C,
∵∠A:∠ADC=1:2,
∴∠A=60°,∠ADC=120°,∴∠C=60°,
∵BE=BC,∴△BCE是等边三角形,∴∠BEC=60°,
∵DC∥AB,∴∠BEC=∠ABE,∴∠ABE=60°,
故选:C.
7、(2020 贵阳模拟)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是 .
【点拨】直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【解析】解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长=AO+OB+AB=8+6=14.
故答案为:14.
8、(2020春 青川县期末)如图,平行四边形ABCD中,AC和BD交于点O,若AC=8,BD=6,则边AD长的取值范围是( )
A.1<AD<7 B.5<AD<11 C.6<AD<8 D.3<AD<4
【点拨】根据平行四边形对角线互相平分可得AO=4,DO=3,再根据三角形的三边关系可得4﹣3<AD<4+3,再解即可.
【解析】解:∵四边形ABCD是平行四边形,
∴AO=AC,DO=BD,
∵AC=8,BD=6,
∴AO=4,DO=3,
∴4﹣3<AD<4+3,
解得:1<AD<7,
故选:A.
9、(2020春 沙坪坝区期末)平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cm
A.14 B.16 C.12或14 D.14或16
【点拨】根据题意画出图形,由平行四边形得出对边平行,又由角平分线可以得出△ABE为等腰三角形,然后分别讨论BE=2cm,CE=3cm或BE=3cm,CE=2cm,继而求得答案.
【解析】解:如图,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DAE=∠AEB,
∵AE为角平分线,∴∠DAE=∠BAE,∴∠AEB=∠BAE,∴AB=BE,
∴①当AB=BE=2cm,CE=3cm时,BC=BE+CE=5cm,
则平行四边形的周长=2(2+5)=14(cm);
②当AB=BE=3cm时,CE=2cm,BC=BE+CE=5cm,
则平行四边形的周长=2(3+5)=16(cm);
故选:D.
10、如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
【分析】本题考查的是平行四边形的判定和性质、等边三角形的性质以及三角形面积等知识,熟练掌握平行四边形的判定与性质和等边三角形的性质,证明四边形BCDF为平行四边形是解题关键.
由平行四边形的判定定理判断②,再由平行四边形的性质和平行线的性质判断①,然后由三角形三边关系判断③,最后由等边三角形的性质分别求出△ACD、△ACB、△ABE的面积,计算即可判断④.
【详解】
解:∵∠ACB=90°,∠ABC=30°,,
∵△ACD是等边三角形,∴∠ACD=60°,
∴∠ACD=∠BAC,∴CD∥AB,
∵F为AB的中点,∴BF=AB,
∴BF∥AB,CD=BF,∴四边形BCDF为平行四边形,故②正确;
∵四边形BCDF为平行四边形,∴DF∥BC,
又∵∠ACB=90°,∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,∴DA+DF>BE,故③错误;
设AC=x,则AB=2x,,
,故④正确;
故选:D.
二、填空题
11、如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,
则____________
【分析】此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ADF与△CBE是等腰三角形是关键.
由平行四边形ABCD中,∠ADC,∠BCD的平分线分别交AB于点F、E,易证得△ADF与△CBE是等腰三角形,又由AB=5,BC=3,即可求得答案.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=5,AD=BC=3,
∴∠AFD=∠CDF,∠DCE=∠BEC,
∵∠ADC,∠BCD的平分线分别交AB于点F、E,
∴∠ADF=∠CDF,∠BCE=∠DCE,
∴∠AFD=∠ADF,∠BCE=∠BEC,
∴AF=AD=3,BC=BE=3,
∴EF=AF+BE-AB=3+3-5=1.
故答案为1.
12、如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
【分析】此题考查平行四边形的性质,全等三角形的判定及性质,熟记全等三角形的判定是解题的关键.
证明△MOD≌△NOB,得到S△MOD=S△NOB,利用平行四边形的性质得到S阴影=,由此求出答案.
【详解】
解:∵四边形ABCD是平行四边形,∴BC,OB=OD,∴∠MDO=∠NBO,
∵∠MOD=∠NOB,∴△MOD≌△NOB,∴S△MOD=S△NOB,
∴S阴影=,
故答案为:1.
13、(2021·山东枣庄·中考真题)如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为_______.
试题分析:坐标与图形变化-旋转
连接AA′、CC′,作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.∵直线MN为:x=1,设直线CC′为y=kx+b,
由题意:, ∴, ∴直线CC′为y=x+,
∵直线EF⊥CC′,经过CC′中点(,), ∴直线EF为y=﹣3x+2,
由得, ∴P(1,﹣1).
14、(2020春 临邑县期末)平行四边形ABCD的对角线AC,BD交于点O,△OAB的周长比△BOC的周长小3cm,若AB=5cm,则平行四边形ABCD的周长是 cm.
【点拨】根据平行四边形性质得出OA=OC,AB=CD,AD=BC,求出BC=8cm,即可得出平行四边形的周长.
【解析】解:∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC,
∵△OAB的周长比△OBC的周长小3cm,∴(BC+OC+OB)﹣(AB+OA+OB)=3cm,
∴BC﹣AB=3cm,∴BC=AB+3cm=8cm,
∴平行四边形ABCD的周长=2(AB+BC)=26cm;
故答案为:26.
15、(2020春 仙居县期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,若AB=5,AD=3,则BD的长为 .
【点拨】根据AC⊥BC,AB=5,AD=3,可以得到AC的长,再根据平行四边形的性质,可以得到DE和BE的长,然后根据勾股定理即可求得BD的长.
【解析】解:∵四边形ABCD是平行四边形,∴AD=BC,
∵AC⊥BC,AB=5,AD=3,∴∠ACB=90°,BC=3,∴AC=4,
作DE⊥BC交BC的延长线于点E,
∵AC⊥BC,∴AC∥DE,
又∵AD∥CE,∴四边形ACED是平行四边形,∴AC=DE,AD=CE,∴DE=4,BE=6,
∵∠DEB=90°,∴BD===2,
故答案为:2.
16、(2020 长春模拟)如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
【点拨】本题主要考查了平行四边形的性质,全等三角形的判定与性质以及等腰三角形的性质的综合运用,解决问题的关键是作辅助线构造全等三角形,利用全等三角形的对应边相等,对应角相等进行推算.
延长AE,BC交于点G,判定△ADE≌△GCE,即可得出CG=AD=5,AE=GE,再根据三线合一即可得到FE⊥AG,进而得出Rt△AEF中,EF=AF=4.
【解析】解:如图,延长AE,BC交于点G,
∵点E是CD的中点,∴DE=CE,
∵平行四边形ABCD中,AD∥BC,∴∠D=∠ECG,
又∵∠AED=∠GEC,∴△ADE≌△GCE,∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,∴AF=GF=3+5=8,
又∵E是AG的中点,∴FE⊥AG,∴Rt△AEF中,EF=AF=4,
故答案为:4.
17、(2019秋 江北区校级期末)如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
【点拨】本题考查了平行四边形的判定和性质的应用,题目是一道综合性比较强的题目,难度适中,解题的关键是把握“化动为静”的解题思想.
当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【解析】解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,∴PD=AD﹣AP=12﹣t,
∵AD∥BC,∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
18、(2020 江西模拟)如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为 .
【点拨】分两种情况:(1)当∠BPC=90°时,①由直角三角形的性质即可得出BP=2;
②当点P在边AD上,AP=DP=2时,由等边三角形的性质和勾股定理求出BP即可;
(2)当∠BCP=90°时,CP=PD=,由勾股定理求出BP即可.
【解析】解:分两种情况:
(1)当∠BPC=90°时,
①点P在AB边上时,∵∠B=60°,∴∠BCP=30°,∴BP=BC=2;
②点P在边AD上,AP=DP=2时,如图2所示:
∵四边形ABCD是平行四边形,∴CD=AB=2,∠D=∠B=60°,
∴DP=CD,∴△PCD是等边三角形,PC=CD=2,
∴BP===2;
(2)当∠BCP=90°时,如图3所示:则CPD=90°,
∵CD=AB=2,∠D=∠ABC=60°,∴∠PCD=30°,
∴PD=CD=1,CP=PD=,∴BP==;
综上所述:当△PBC为直角三角形时,BP的长为2或2或.
故答案为:2或2或.
三、解答题
19、(2020 衢州模拟)如图,在 ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
【点拨】本题中,在连接BD交AC于O,则可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
【解析】证明:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO
∵AE=CF,
∴AO﹣AE=CO﹣CF.
即EO=FO.
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形).
20、(2020·广西中考真题)如图,在平面直角坐标系中,的三个顶点分别是A(1,3),B(4,4),
C(2,1).
(1)把向左平移4个单位后得到对应的A1B1C1,请画出平移后的A1B1C1;
(2)把绕原点O旋转180°后得到对应的A2B2C2,请画出旋转后的A2B2C2;
(3)观察图形可知,A1B1C1与A2B2C2关于点( , )中心对称.
【分析】
(1)依据平移的方向和距离,即可得到平移后的△A1B1C1;
(2)依据△ABC绕原点O旋转180°,即可画出旋转后的△A2B2C2;
(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.
【详解】
解:(1)如图所示,分别确定平移后的对应点,
得到A1B1C1即为所求;
(2)如图所示,分别确定旋转后的对应点,
得到A2B2C2即为所求;
(3)由图可得,A1B1C1与A2B2C2关于点成中心对称.
故答案为:﹣2,0.
21、(2020秋 招远市期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
【点拨】本题考查了平行四边形的性质和判定,全等三角形的性质和判定,等腰三角形的判定和平行线的性质等知识点,能综合运用定理进行推理是解此题的关键.
(1)根据平行四边形的性质得出AD∥BC,AB=CD,根据平行线的性质得出∠DAE=∠AEB,求出∠BAE=∠AEB,根据等腰三角形的判定得出即可;
(2)根据等腰三角形的性质得出AF=EF,求出△ADF≌△ECF,根据全等三角形的性质得出DF=CF,再根据平行四边形的判定得出即可.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,
∴BE=AB,∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,∴AF=EF,
在△ADF和△ECF中,,∴△ADF≌△ECF(ASA),∴DF=CF,
又∵AF=EF,∴四边形ACED是平行四边形.
22、(2019春 西湖区校级月考)如图,在 ABCD中,AP、BP分别是∠DAB和∠CBA的角平分线,已知AD=5.
(1)求线段AB的长;
(2)延长AP,交BC的延长线于点Q.
①请在答卷上补全图形;
②若BP=6,求△ABQ的周长.
【点拨】(1)依据平行线的性质以及角平分线的定义即可得到DP=AD=5,CP=BC=5,进而得出AB的长;
(2)依据平行线的性质以及角平分线的定义即可得到AB=QB,再根据BP平分∠ABQ,即可得出BP⊥AQ,AP=QP,依据勾股定理得出AP的长,进而得到△ABQ的周长.
【解析】解:(1)∵在 ABCD中,AD=5,∴BC=5,
∵AB∥CD,∴∠BAP=∠DPA,
∵AP平分∠BAD,∴∠BAP=∠DAP,∴∠DAP=∠DPA,∴DP=AD=5,
同理可得,CP=BC=5,∴CD=10,∴AB=10;
(2)①如图所示:
②∵AD∥BQ,∴∠Q=∠DAP,
又∵∠DAP=∠BAP,∴∠Q=∠BAP,∴AB=QB=10,
又∵BP平分∠ABQ,∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP===8,
∴AQ=16,∴△ABQ的周长为:16+10+10=36.
23、(2019春 虹口区期中)如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
【点拨】(1)证△DEC≌△AEF(AAS),得出DC=FA,进而得出结论;
(2)由平行四边形的对边平行证出∠CBF=∠DAF=70°,∠AEB=∠EBC,由等腰三角形的性质得出∠AEB=∠ABE,即可得出答案.
【解析】(1)证明∵E为AD的中点,∴DE=AE,
∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC,∴∠EDC=∠EAF,
在△DEC和△AEF中,,∴△DEC≌△AEF(AAS),∴DC=FA,
∵AD=2AB,∴AB=DE=EA=FA,∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,∴∠AEB=∠ABE,∴∠EBC=∠ABE=35°.
24、(2020 杭州模拟)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
【点拨】(1)先证△AEF≌△CED(AAS),得AF=CD,再由CD∥AB,即AF∥CD,即可得出结论;
(2)过C作CM⊥AB于M,先证△BCM是等腰直角三角形,得BM=CM,再由含30°角的直角三角形的性质得AC=2AM,BM=CM=AM,由AM+BM=AB求出AM=3﹣3,即可求解.
【解析】(1)证明:∵E是AC的中点,∴AE=CE,
∵CD∥AB,∴∠AFE=∠CDE,
在△AEF和△CED中,,∴△AEF≌△CED(AAS),∴AF=CD,
又∵CD∥AB,即AF∥CD,∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:则∠CMB=∠CMA=90°,
∵CD∥AB,∴∠B+∠DCB=180°,∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,∴BM=CM,
∵∠BAC=60°,∴∠ACM=30°,∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,∴AM+AM=6,解得:AM=3﹣3,∴AC=2AM=6﹣6.
25、(2018春 鄂城区期中)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
【点拨】本题考查了平行四边形的判定、等腰直角三角形的判定与性质、等腰三角形的性质等知识;根据题意得出t的方程是解决问题的突破口.
(1)作AM⊥BC于M,由已知条件得出AB=AC,由等腰三角形的性质得出BM=CM,由直角三角形斜边上的中线性质得出AM=BC=5,证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5﹣t,由CE=CQ﹣QE=2t﹣2得出方程,解方程即可;
(2)由平行四边形的判定得出AP=BE,得出方程,解方程即可.
【解析】解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,
∴BM=CM,∴AM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10, 解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
26、如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=,且BF=DF,求旋转角度α的大小.
【分析】此题是四边形综合题,主要考查了平行四边形的性质和判定,全等三角形的判定和性质,等腰三角形的判定和性质,等腰直角三角形的性质,旋转的性质,判断出△ABO是等腰直角三角形是解本题的关键.
(1)由平行四边形的性质得出∠OAF=∠OCE,OA=OC,进而判断出△AOF≌△COE,即可得出结论;
(2)先判断出∠BAC=∠AOF,得出AB∥EF,即可得出结论;
(3)先求出AC=2,进而得出A=1=AB,即可判断出△ABO是等腰直角三角形,进一步判断出△BFD是等腰三角形,利用等腰三角形的三线合一得出∠BOF=90°,即可得出结论.
【详解】
(1)证明:在 ABCD中,AD∥BC,∴∠OAF=∠OCE,
∵OA=OC,∠AOF=∠COE,∴△AOF≌△COE(ASA),∴OE=OF;
(2)当旋转角为90°时,四边形ABEF是平行四边形,理由:
∵AB⊥AC,∴∠BAC=90°,
∵∠AOF=90°,∴∠BAC=∠AOF,∴AB∥EF,
∵AF∥BE,∴四边形ABEF是平行四边形;
(3)在Rt△ABC中,AB=1,BC=,∴AC==2,
∴OA=1=AB,∴△ABO是等腰直角三角形,∴∠AOB=45°,
∵BF=DF,∴△BFD是等腰三角形,
∵四边形ABCD是平行四边形,∴OB=OD,
∴OF⊥BD(等腰三角形底边上的中线是底边上的高),
∴∠BOF=90°,∴∠α=∠AOF=∠BOF﹣∠AOB=45°.
27、(2020·浙江嘉兴·中考真题)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.
(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
【答案】【思考】是,理由见解析;【发现】;【探究】BD=2OF,理由见解析;
【分析】本题考查了图形的综合变换,涉及了三角形全等的判定与性质、平行四边形的判定与性质等,准确识图,熟练掌握和灵活运用相关知识是解题的关键.
【思考】由全等三角形的性质得出AB=DE,∠BAC=∠EDF,则AB∥DE,可得出结论;
【发现】连接BE交AD于点O,设AF=x(cm),则OA=OE=(x+4),得出OF=OA﹣AF=2﹣x,由勾股定理可得,解方程求出x,则AF可求出;
【探究】如图2,延长OF交AE于点H,证明△EFO≌△EFH(ASA),得出EO=EH,FO=FH,则∠EHO=∠EOH=∠OBD=∠ODB,可证得△EOH≌△OBD(AAS),得出BD=OH,则结论得证.
【详解】
解:【思考】四边形ABDE是平行四边形.
证明:如图,∵△ABC≌△DEF,
∴AB=DE,∠BAC=∠EDF,∴AB∥DE,∴四边形ABDE是平行四边形;
【发现】
如图1,连接BE交AD于点O,
∵四边形ABDE为矩形,∴OA=OD=OB=OE,
设AF=x(cm),则OA=OE=(x+4),∴OF=OA﹣AF=2﹣x,
在Rt△OFE中,∵OF2+EF2=OE2,
∴,解得:x=,∴AF=cm.
【探究】BD=2OF,
证明:如图2,延长OF交AE于点H,
∵四边形ABDE为矩形,∴∠OAB=∠OBA=∠ODE=∠OED,OA=OB=OE=OD,
∴∠OBD=∠ODB,∠OAE=∠OEA,
∴∠ABD+∠BDE+∠DEA+∠EAB=360°,∴∠ABD+∠BAE=180°,
∴AE∥BD,∴∠OHE=∠ODB,
∵EF平分∠OEH,∴∠OEF=∠HEF,
∵∠EFO=∠EFH=90°,EF=EF,∴△EFO≌△EFH(ASA),∴EO=EH,FO=FH,
∴∠EHO=∠EOH=∠OBD=∠ODB,
∴△EOH≌△OBD(AAS),∴BD=OH=2OF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
