2021—2022学年苏科版数学八年级下册9.5专题练平行四边形与中位线(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.5专题练平行四边形与中位线(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1023.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 14:10:18 | ||
图片预览



文档简介
专题练:平行四边形与中位线
-2021-2022学年八年级数学下册(苏科版)
一、选择题
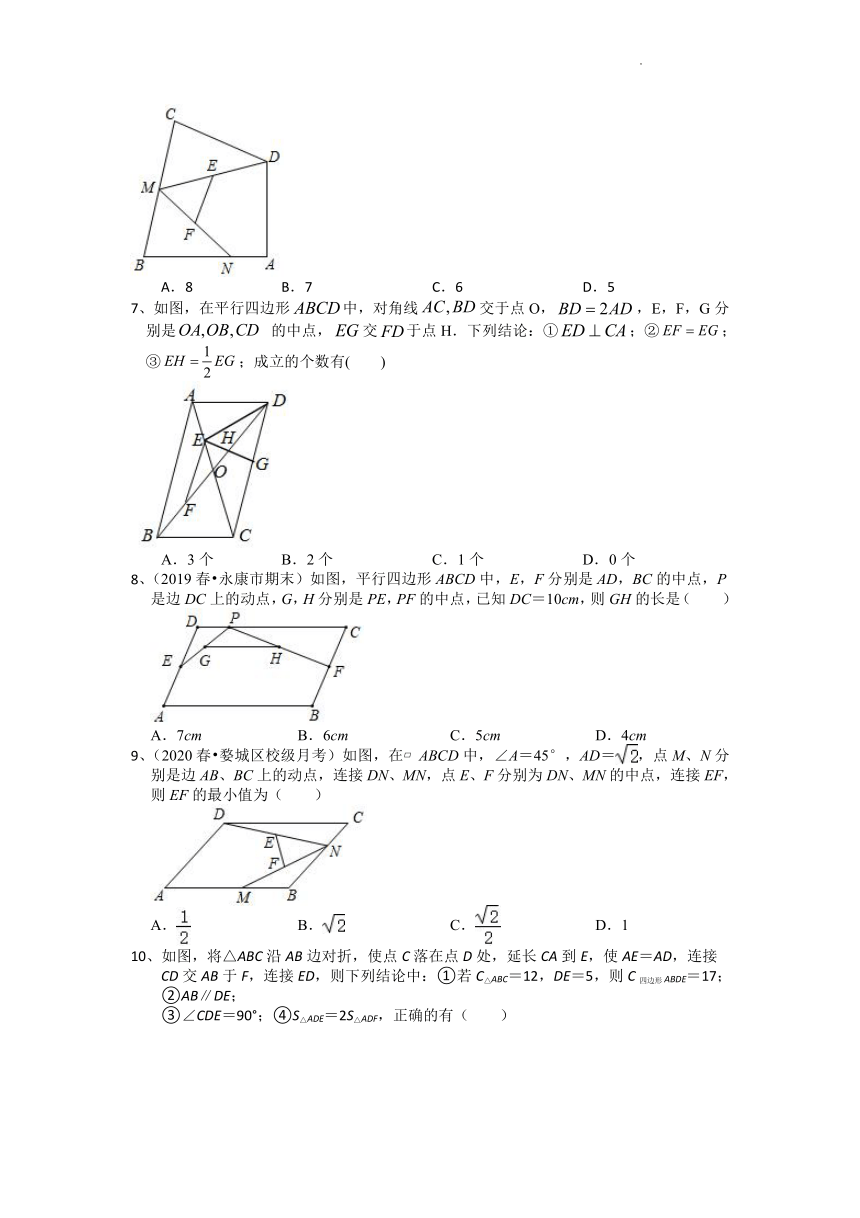
1、(2020春 湖州期末)如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( )
A.8cm B.5cm C.3cm D.2cm
2、(2020春 长兴县期中)如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10 C.12 D.14
3、(2021 河南模拟)如图, ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5 B.2 C.2.5 D.3
4、如图,△ABC的边AB,BC,CA的中点分别是D,E,F,已知AB=8,AC=10,则四边形ADEF的周长是( )
A.8 B.9 C.10 D.18
5、(2020春 北仑区期末)如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
6、如图,四边形中,,,,点,分别为线段,上的动点(含端点,但点不与点重合),点,分别为,的中点,则长度的最大值为( )
A.8 B.7 C.6 D.5
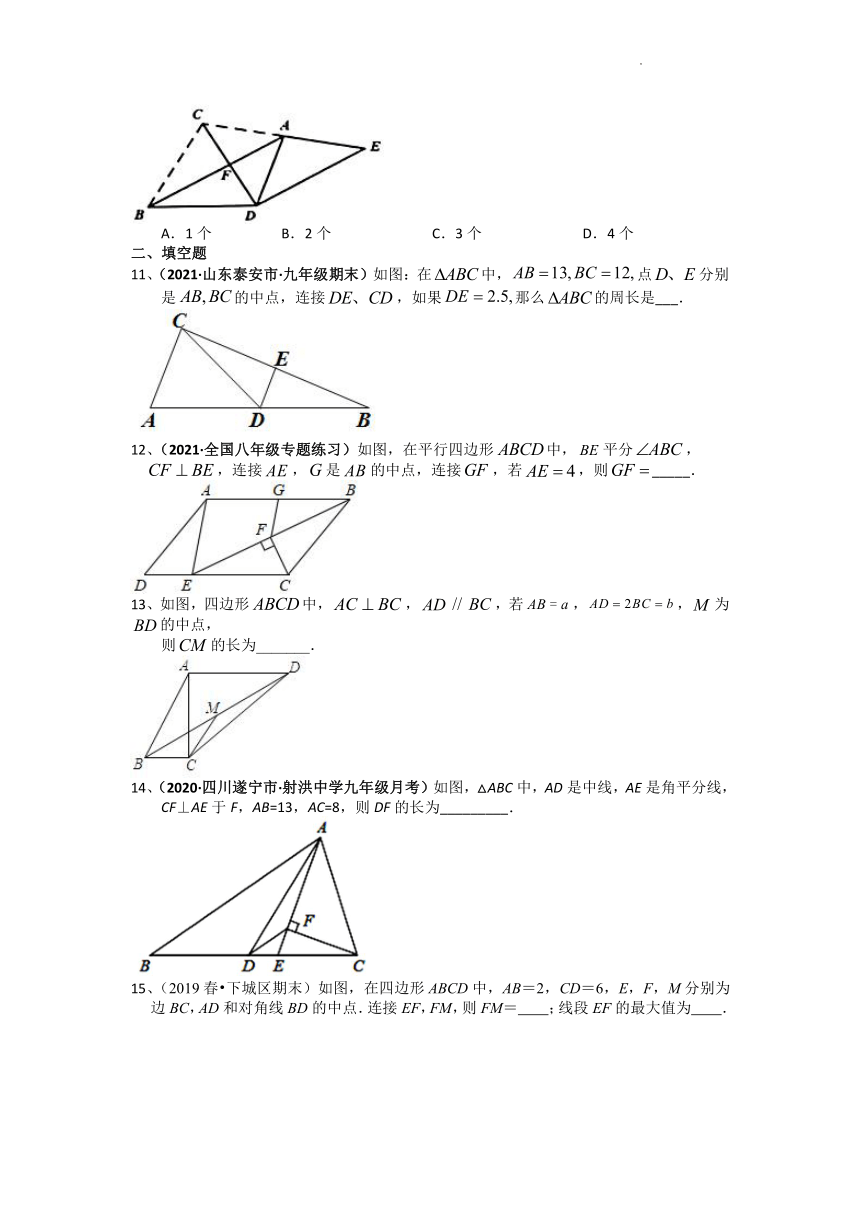
7、如图,在平行四边形中,对角线交于点O,,E,F,G分别是 的中点,交于点H.下列结论:①;②;③;成立的个数有( )
A.3个 B.2个 C.1个 D.0个
8、(2019春 永康市期末)如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( )
A.7cm B.6cm C.5cm D.4cm
9、(2020春 婺城区校级月考)如图,在 ABCD中,∠A=45°,AD=,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A. B. C. D.1
10、如图,将△ABC沿AB边对折,使点C落在点D处,延长CA到E,使AE=AD,连接CD交AB于F,连接ED,则下列结论中:①若C△ABC=12,DE=5,则C四边形ABDE=17;②AB∥DE;
③∠CDE=90°;④S△ADE=2S△ADF,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
12、(2021·全国八年级专题练习)如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
13、如图,四边形中,,,若,,为的中点,
则的长为_______.
14、(2020·四川遂宁市·射洪中学九年级月考)如图,△ABC中,AD是中线,AE是角平分线, CF⊥AE于F,AB=13,AC=8,则DF的长为_________.
15、(2019春 下城区期末)如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点.连接EF,FM,则FM= ;线段EF的最大值为 .
16、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
17、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E在线段上且,点F是边的中点,若,,且,则的长是_______.
18、如图,已知,点A在边OX上,,过点A作于点C,以AC为一边在内作等边三角形ABC,点P是围成的区域(包括各边)内的一点,过点P作交OX于点D,作交OY于点E,则的最大值与最小值的积是______.
三、解答题
19、(2020春 临海市期末)如图,在 ABCD中,点F是边AB的中点,连接DF并延长交CB的延长线于点E.求证:EB=BC.
20、如图,在△ABC中,D是BC上一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
21、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E,点F分别是 的中点.连结 .
(1)求证:四边形是平行四边形.
(2)若平分,求平行四边形的周长.
22、(2019春 岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
23、在中,,E、F分别是、的中点,延长到点D,使,连接、、、,与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
24、(2020春 兰州期末)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=4,求DG的长度.
25、如图,在中有如下3个论断;①点是的边的中点;②点是边的中点;③.选择其中两个作为题设另一个为结论,可以写出所有以下三个命题,(1):①②③,(2):①③②,(3):②③①.
(1)正确的命题有______.(填番号)
(2)请对命题(2)的正误作出证明.
26、(2020 长春模拟)【感知】如图①,BD、CE分别是△ABC的外角平分线,过点A作AM⊥BD于M,AN⊥CE于N,连接MN,易证:MN=(AB+BC+AC)(不需要证明).
【探究】如图②,若BD、CE分别是△ABC的两个内角的平分线,且AM⊥BD于M,AN⊥CE于N,连接MN.试猜想MN与边AB、AC和BC之间的数量关系,并证明你的结论.
【应用】如图③,在四边形ABCD中,∠ABC=∠ADC=90°,射线BE平分∠ABC,AM⊥BE于点M,连接MD,延长BC至F,若∠DCF=∠ACD=75°,AB=2,直接写出MD的长度.
专题练:平行四边形与中位线
-2021-2022学年八年级数学下册(苏科版)(解析)
一、选择题
1、(2020春 湖州期末)如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( )
A.8cm B.5cm C.3cm D.2cm
【点拨】根据平行四边形的性质,可以得到AE=CE,AD=BC,再根据△ABE的周长比△BEC的周长小3cm,AB=5cm,即可得到BC的长,从而可以得到AD的长,本题得以解决.
【解析】解:∵四边形ABCD是平行四边形,
∴AE=CE,AD=BC,
∵△ABE的周长比△BEC的周长小3cm,
∴(BC+CE+BE)﹣(AB+AE+BE)=3,
∴BC﹣AB=3,
∵AB=5cm,
∴BC=8cm,
∴AD=8cm,
故选:A.
2、(2020春 长兴县期中)如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10 C.12 D.14
【点拨】根据线段中点的性质、三角形中位线定理得到BD=AB,BE=BC,DE=AC,计算即可.
【解析】解:∵点D、E分别是边AB、BC的中点,
∴BD=AB,BE=BC,DE=AC,
∴AB=2BD,BC=2BE,AC=2DE,
∴△ABC的周长=AB+BC+AC=2BD+2BE+2DE=2(BD+BE+DE)=2×△DBE的周长=2×7=14,
故选:D.
3、(2021 河南模拟)如图, ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5 B.2 C.2.5 D.3
【点拨】根据平行四边形的性质得出OA=3,OB=5,进而利用勾股定理得出AB的长,利用三角形中位线得出OE即可.
【解析】解:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴OA=3,OB=5,AB∥DC,
∵∠OCD=90°,
∴∠BAO=90°,
∴AB=,
∵E是BC边的中点,OA=OC,
∴2OE=AB,
∴OE=2,
故选:B.
4、如图,△ABC的边AB,BC,CA的中点分别是D,E,F,已知AB=8,AC=10,则四边形ADEF的周长是( )
A.8 B.9 C.10 D.18
【答案】D
【分析】本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
根据线段中点的概念求出AD、AF,根据三角形中位线定理求出DE、EF,计算即可.
【详解】解:∵△ABC的边AB、BC、CA的中点分别是D、E、F,
∴AD=AB=4,AF=AC=5,DE=AC=5,EF=AB=4,
∴四边形ADEF的周长=4+5+5+4=18,
故选:D.
5、(2020春 北仑区期末)如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
【点拨】此题考查了三角形的中位线定理,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
根据勾股定理得到AB=5,根据平行线的性质和角平分线的定义得到∠ABD=∠ADB,求得AB=AD=5,连接BF并延长交AD于G,根据全等三角形的性质得到BF=FG,AG=BC=3,求得DG=5﹣3=2,根据三角形中位线定理即可得到结论.
【解析】解:∵AC⊥BC,∴∠ACB=90°,
∵BC=3,AC=4,∴AB=5,
∵AD∥BC,∴∠ADB=∠DBC,
∵BD为∠ABC的平分线,∴∠ABD=∠CBD,
∴∠ABD=∠ADB,∴AB=AD=5,
连接BF并延长交AD于G,
∵AD∥BC,∴∠GAC=∠BCA,
∵F是AC的中点,∴AF=CF,
∵∠AFG=∠CFB,∴△AFG≌△CFB(AAS),
∴BF=FG,AG=BC=3,∴DG=5﹣3=2,
∵E是BD的中点,∴EF=DG=1.
故选:A.
6、如图,四边形中,,,,点,分别为线段,上的动点(含端点,但点不与点重合),点,分别为,的中点,则长度的最大值为( )
A.8 B.7 C.6 D.5
【分析】本题考查的是三角形中位线定理、勾股定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
连接DN,根据三角形中位线定理得到EF=DN,根据题意得到当点N与点B重合时,DN最大,根据勾股定理计算,得到答案.
【详解】
解:连接DN,
∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
7、如图,在平行四边形中,对角线交于点O,,E,F,G分别是 的中点,交于点H.下列结论:①;②;③;成立的个数有( )
A.3个 B.2个 C.1个 D.0个
【答案】A
【分析】本题考查了平行四边形性质和判定,三角形中位线定理,三角形面积,直角三角形斜边上中线等于斜边一半,等腰三角形性质等;熟练运用三角形中位线定理、等腰三角形“三线合一”、直角三角形斜边上中线等于斜边一半等性质是解题关键.
由平行四边形性质和等腰三角形“三线合一”即可得ED⊥CA,根据三角形中位线定理可得EF =AB;由直角三角形斜边上中线等于斜边一半可得EG=CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得EH=EG.
【详解】
解:如图,连接FG,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC,AD∥BC,AB=CD,AB∥CD,
∵BD=2AD,∴OD=AD,∵点E为OA中点,∴ED⊥CA,故①正确;
∵E,F,G分别是OA,OB,CD的中点,∴EF∥AB,EF=AB,
∵∠CED=90°,CG=DG=CD,∴EG=CD,∴EF=EG,故②正确;
∵EF∥CD,EF=DG,∴四边形DEFG是平行四边形,
∴EH=HG,即EH=EG,故③正确;
故选:A.
8、(2019春 永康市期末)如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( )
A.7cm B.6cm C.5cm D.4cm
【点拨】本题主要考查了平行四边形的性质以及三角形中位线定理的知识,解题的关键是证明出GH是△PEF的中位线,此题难度不大.
连接EF,先证明出四边形ABFE是平行四边形,再证明GH是△PEF的中位线,进而求出GH的长度.
【解析】解:连接EF,
∵四边形ABCD是平行四边形,∴AB=CD,AD=BD,AD∥BC,
∵E,F分别是AD,BC的中点,∴AE=BF,
∴四边形ABFE是平行四边形,∴AB=EF=10cm,
∵G,H分别是PE,PF的中点,∴GH是△PEF的中位线,
∴GH=EF=×10=5cm,
故选:C.
9、(2020春 婺城区校级月考)如图,在 ABCD中,∠A=45°,AD=,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A. B. C. D.1
【点拨】本题考查平行四边形的性质、三角形的中位线定理、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是确定EF的最小值,就是DM的最小值.
连接DM,利用三角形中位线定理,可知EF=DM,求出DM的最小值即可求出EF的最小值.
【解析】解:如图,连接DM,
∵E、F分别为DN、MN的中点,
∴EF=DM,
∴EF的最小值,就是DM的最小值,
当DM⊥AB时,DM最小,
Rt△ADM中,∠A=45°,AD=,
∴DM=AD=1,
∴EF=DM=,
∴EF的最小值是.
故选:A.
10、如图,将△ABC沿AB边对折,使点C落在点D处,延长CA到E,使AE=AD,连接CD交AB于F,连接ED,则下列结论中:①若C△ABC=12,DE=5,则C四边形ABDE=17;②AB∥DE;
③∠CDE=90°;④S△ADE=2S△ADF,正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】本题主要考查了图形的翻折,三角形的面积,平行线的判定和性质等知识点,熟练应用同位角相等两直线平行,内错角相等两直线平行,两直线平行同位角相等是解题的关键.
①由题知AE=AC,BD=BC,可得结论正确;
②由三角形外角知∠CAB+∠DAB=∠ADE+∠AED,又知∠CAB=∠DAB,∠ADE=∠AED,即可得∠CAB=∠DAB=∠ADE=∠AED,即可得证结论;
③由对称知CD⊥AB,由AB∥DE可得结论;
④由③知S△ADE=DF DE,S△ADF=DF AF,证AF是中位线可得AF=DE,即可得证结论.
【详解】
解:①由图形翻折可知,AD=AC,BD=BC,
∵AE=AD,∴AE=AC,∴C四边形ABDE=C△ABC+DE,
∵C△ABC=12,DE=5,∴C四边形ABDE=17,故①正确;
②由图形翻折知,∠CAB=∠DAB,
∵AE=AD,∴∠ADE=∠AED,
又∵∠CAB+∠DAB=∠ADE+∠AED,∴∠CAB=∠DAB=∠ADE=∠AED,∴AB∥DE,故②正确;
③由②知,AB∥DE,
由图形翻折知,CD⊥AB,∴∠CFA=∠CDE=90°,故③正确;
④由③知,∠CFA=∠CDE=90°,∴S△ADE=DF DE,S△ADF=DF AF,
∵AE=AC,AB∥DE,CF=DF,∴AF是△DEF的中位线,∴AF=DE,∴S△ADE=2S△ADF,故④正确,
故选:D.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
【答案】30
【分析】根据三角形的中位线性质,求出AC的长,再求出ΔABC的周长.
【详解】∵点 D 、 E 分别是 AB 、 BC 的中点,∴DE是ΔABC的中位线,∴ DE=AC ,
∵ DE=2.5 ,∴ AC=5 ,∵ AB=13 , BC=12 ,∴ C△ABC=AB+BC+AC=13+12+5=30.
故答案为:30.
12、(2021·全国八年级专题练习)如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
【答案】2
【分析】根据平行四边形的性质结合角平分线的定义可求解,即可得,利用等腰三角形的性质得到,进而可得是的中位线,根据三角形的中位线的性质可求解.
【详解】解:在平行四边形中,,∴,
∵平分,∴,∴,∴,
∵,∴,∵是的中点,∴是的中位线,∴
∵,∴;故答案为:2.
13、如图,四边形中,,,若,,为的中点,
则的长为_______.
【答案】
【分析】本题考查平行四边形的判定与性质、中位线的性质等知识,是重要考点,难度较易,掌握相关知识、作出正确的辅助线是解题关键.
延长,使,根据题意先证明四边形是平行四边形,可解得,继而得到是的中点,再结合中位线的性质解题即可.
【详解】解:延长,使,
四边形是平行四边形,∴DE=AB,
,
是的中点,
为的中点,
故答案为:.
14、(2020·四川遂宁市·射洪中学九年级月考)如图,△ABC中,AD是中线,AE是角平分线, CF⊥AE于F,AB=13,AC=8,则DF的长为_________.
【答案】2.5
【分析】延长CF交AB于H,证明△AFH≌△AFC,根据全等三角形的性质得到AH=AC=7,CF=FH,求出HB,根据三角形中位线定理计算即可.
【详解】解:延长CF交AB于H,
∵AE平分∠BAC,∴∠HAF=∠CAF,
在△AFH和△AFC中, ,
∴△AFH≌△AFC(ASA),∴AH=AC,CF=FH,
∵AB=13,AC=8,∴AH=AC=8,∴HB=AB-AH=13-8=5,
∵CF=FH,CD=DB,∴DF=HB=2.5,故答案为:2.5.
15、(2019春 下城区期末)如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点.连接EF,FM,则FM= ;线段EF的最大值为 .
【点拨】此题考查三角形中位线定理,关键是利用三角形的中位线平行于第三边,并且等于第三边的一半解答.
连接EM,利用三角形中位线定理解答即可.
【解析】解:连接EM,
∵E,F,M分别为边BC,AD和对角线BD的中点,
∴FM=,EM=,
当EF=EM+MF时,线段EF最大,即EF=1+3=4,
故答案为:1;4.
16、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
【答案】①④
【分析】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的性质等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.
根据全等三角形的判定与性质和平行四边形的判定与性质分别推理论证,即可得到结论.
【详解】解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,∴BF-OB=DE-OD,即OF=OE,∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,∴不能判定四边形AECF是平行四边形;
③∠EAB=∠FCO不能判定四边形AECF平行四边形;
④∵AF∥CE,∴∠AFB=∠CED,
在△ABF和△CDE中,,∴△ABF≌△CDE(AAS),∴BF=DE,
∴BF-OB=DE-OD,即OF=OE,
又∵OA=OC,∴四边形AECF是平行四边形;
故答案为:①④.
17、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E在线段上且,点F是边的中点,若,,且,则的长是_______.
【答案】
【分析】本题考查了平行四边形的判定与性质,三角形中位线定理,勾股定理,解决本题的关键是掌握平行四边形的判定与性质.
过点作于点,过点作交于点,连接,可得是等腰直角三角形,证明是三角形的中位线,可得四边形是平行四边形,再根据勾股定理即可得的长.
【详解】解:如图,过点作于点,过点作交于点,连接,
,是等腰直角三角形,,
,,,
,,是三角形的中位线,
,,,
点是边的中点,,,,
四边形是平行四边形,,
,,,,
,,,
,.
故答案为:.
18、如图,已知,点A在边OX上,,过点A作于点C,以AC为一边在内作等边三角形ABC,点P是围成的区域(包括各边)内的一点,过点P作交OX于点D,作交OY于点E,则的最大值与最小值的积是______.
【答案】40
【分析】
结合题意,得四边形ODPE是平行四边形,从而得到;结合点P是围成的区域(包括各边)内的一点,推导得当点P在AC上时,取最小值;当点P与点B重合时,取最大值;再分别根据两种情况,结合平行四边形、等边三角形、勾股定理的性质计算,即可完成求解.
【详解】
过点P做交于点H
∵∴
∵∴ ∴
∵,∴四边形ODPE是平行四边形
∴,∴
∴
∵点P是围成的区域(包括各边)内的一点
结合图形,得:当点P在AC上时,取最小值;当点P与点B重合时,取最大值;
当点P在AC上时,
∵,,∴,∴最小值;
当点P与点B重合时,如下图,AC和BD相交于点G
∴
∵,,
∴ , ,
∵等边三角形ABC,∴ ,
∴
∴ ,∴
∴GB是等边三角形ABC的角平分线,∴
又∵,即 ,∴是的中位线,∴
∴, ,∴
∵,∴ ,∴
∴,∴最大值
∴最大值与最小值的积
故答案为:40.
三、解答题
19、(2020春 临海市期末)如图,在 ABCD中,点F是边AB的中点,连接DF并延长交CB的延长线于点E.求证:EB=BC.
【点拨】本题考查了平行四边形性质,全等三角形的性质和判定,平行线的性质的应用,关键是推出△ADF≌△BEF.
根据平行四边形性质得出AD=BC,AD∥BC,推出∠A=∠FBE,∠ADF=∠E,证△ADF≌△BEF,推出BE=DA即可.
【解析】解:∵F是AB边的中点,
∴AF=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠A=∠FBE,∠ADF=∠E,
在△ADF和△BEF中,
∴△ADF≌△BEF(AAS),
∴AD=BE,
∵AD=BC,
∴EB=BC.
20、如图,在△ABC中,D是BC上一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
【分析】根据三角形的中位线定理可判定四边形EFGH为平行四边形,根据平行四边形的性质即可得到EG、HF互相平分.
【详解】连结EH、FG.,
∵E、H分别是BD、AD的中点,∴EH∥AB ,EH=AB.
同理,FG∥AB ,FG=AB.
∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形,∴EG、HF互相平分.
21、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E,点F分别是 的中点.连结 .
(1)求证:四边形是平行四边形.
(2)若平分,求平行四边形的周长.
【答案】(1)见解析;(2)18
【分析】(1)由平行四边形的性质和中点的性质可得DE=BF,即可得结论;
(2)由角平分线的性质和平行线的性质可证AB=AE=3,即可求解.
【详解】解:证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∵点E,点F分别是AD,BC的中点,
∴AE=DE=AD,BF=CF=BC,∴DE=BF,
又∵DE∥BF,∴四边形BEDF是平行四边形;
(2)∵BE平分∠ABC,∴∠ABE=∠EBC,
又∵AD∥BC,∴∠AEB=∠EBC,
∴∠ABE=∠AEB,∴AE=AB=3,∴AD=2AE=6,
∴平行四边形ABCD的周长=2×(3+6)=18.
22、(2019春 岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
【点拨】连接DE,FG,由BD与CE为中位线,利用中位线定理得到ED与BC平行,FG与BC平行,且都等于BC的一半,等量代换得到ED与FG平行且相等,进而得到四边形EFGD为平行四边形,利用平行四边形的性质即可得证.
【解析】证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
23、在中,,E、F分别是、的中点,延长到点D,使,连接、、、,与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
【答案】(1)理由见详解;(2)
【分析】本题主要考查三角形中位线、平行四边形的判定与性质及勾股定理,熟练掌握三角形中位线、平行四边形的判定与性质及勾股定理是解题的关键.
(1)由题意易得,,进而可得,则四边形是平行四边形,然后问题得证;
(2)由(1)可得,,,由勾股定理可得,进而可得,然后根据勾股定理可求解.
【详解】
解:(1)∵E、F分别是、的中点,∴,,
∵,∴
∴四边形是平行四边形,∴与互相平分;
(2)由(1)得:与互相平分,,,
∵,∴,,,
∵,∴,
∴,∴,
∴,∴.
24、(2020春 兰州期末)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=4,求DG的长度.
【点拨】本题考查了平行四边形的判定与性质、三角形中位线定理,解决本题的关键是综合运用平行四边形的判定与性质、三角形中位线定理.
(1)根据三角形中位线定理即可证明四边形DEFG是平行四边形;
(2)根据OB⊥OC,∠EOM和∠OCB互余,可以证明OM=MF,OM=EM,可得EF=2OM=8,由(1)有四边形DEFG是平行四边形,可得DG=EF=8.
【解析】解:(1)证明:∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,
同理EF∥BC,EF=BC,
∴DG=EF,DG∥EF,∴四边形DEFG是平行四边形;
(2)∵OB⊥OC∴∠BOC=90°,
∵∠EOM+∠COM=90°,∠EOM+∠OCB=90°,∴∠COM=∠OCB,
∵EF∥BC,∴∠OFE=∠OCB,∴∠MOF=∠MFO,∴OM=MF,
∵∠OEM+∠OFM=90°,∠EOM+∠MOF=90°
∴∠EOM=∠MEO,∴OM=EM,∴EF=2OM=8,
由(1)有四边形DEFG是平行四边形,∴DG=EF=8.
25、如图,在中有如下3个论断;①点是的边的中点;②点是边的中点;③.选择其中两个作为题设另一个为结论,可以写出所有以下三个命题,(1):①②③,(2):①③②,(3):②③①.
(1)正确的命题有______.(填番号)
(2)请对命题(2)的正误作出证明.
【答案】(1)(1)、(2)、(3);(2)证明见解析
【分析】本题考查中位线定理,解题的关键是掌握中位线定理的证明方法,通过构造全等三角形和平行四边形的性质和判断去证明中位线定理.
(1)这三个命题都是正确的,利用构造全等三角形的方法和平行四边形的性质和判定证明命题的正确性;
(2)延长至点,使,连接,证明,得到四边形为平行四边形,就可以证明结论.
【详解】
(1)命题(1):延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴,
∵为中点,∴,∴,
∴四边形为平行四边形,∴即;
命题(2):延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴即,
∵即,∴四边形为平行四边形,∴,
又∵,∴,∴点为的中点;
命题(3):延长线段至点,使得,
如下图:连接,
∵点为的中点,∴,
在中和中,,∴(SAS),
∴且,
由可得:,即,
又∵即,∴四边形为平行四边形,∴,
又∵,∴,则点为的中点;
(2)延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴即,
∵即,∴四边形为平行四边形,∴,
又∵,∴,∴点为的中点.
26、(2020 长春模拟)【感知】如图①,BD、CE分别是△ABC的外角平分线,过点A作AM⊥BD于M,AN⊥CE于N,连接MN,易证:MN=(AB+BC+AC)(不需要证明).
【探究】如图②,若BD、CE分别是△ABC的两个内角的平分线,且AM⊥BD于M,AN⊥CE于N,连接MN.试猜想MN与边AB、AC和BC之间的数量关系,并证明你的结论.
【应用】如图③,在四边形ABCD中,∠ABC=∠ADC=90°,射线BE平分∠ABC,AM⊥BE于点M,连接MD,延长BC至F,若∠DCF=∠ACD=75°,AB=2,直接写出MD的长度.
【点拨】本题考查四边形综合题,考查了等腰三角形的判定和性质,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,应用三角形中位线定理解决问题.
【感知】如图①,设AN的延长线交BC的延长线于K,AM的延长线交CB的延长线于J.利用三角形的中位线定理解决问题即可.
【探究】如图②,结论:MN=(AB+AC﹣BC).利用三角形的中位线定理解决问题即可.
【应用】如图③中,延长AM交BC于J,延长AD交BC的延长线于K.利用DM=(AC+BC﹣AC)求解即可.
【解析】解:【感知】如图①中,设AN的延长线交BC的延长线于K,AM的延长线交CB的延长线于J.
∵AM⊥BD,∴∠AMB=∠BMJ=90°,
∵∠ABM=∠JBM,∠ABM+∠BAM=90°,∠JBM+∠J=90°,
∴∠BAM=∠J,∴BA=BJ,同法可证:CA=CK,
∴AM=MJ,AN=NK,∴MN=JK=(JB+BC+CK)=(AB+BC+AC).
【探究】如图②中,结论:MN=(AB+AC﹣BC).
理由:延长AM交BC于F,延长AN交BC于G.
∵AM⊥BD,∴∠AMB=∠BMF=90°,
∵∠ABM=∠FBM,∠ABM+∠BAM=90°,∠FBM+∠BFM=90°,
∴∠BAM=∠BFM,∴BA=BF,同法可证:CA=CG,
∴AM=MF,AN=NG,∴MN=FG=(BF+CG﹣BC)=(AB+AC﹣BC).
【应用】如图③中,延长AM交BC于J,延长AD交BC的延长线于K.
由题意∠ACB=180°﹣∠ACD﹣∠DCF=30°,
∵∠ABC=90°,AB=2,∴AC=2AB=4,BC=AB=2,
同法可证DM=JK=(AC+BC﹣AB)=(4+2﹣2)=1+.
-2021-2022学年八年级数学下册(苏科版)
一、选择题
1、(2020春 湖州期末)如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( )
A.8cm B.5cm C.3cm D.2cm
2、(2020春 长兴县期中)如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10 C.12 D.14
3、(2021 河南模拟)如图, ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5 B.2 C.2.5 D.3
4、如图,△ABC的边AB,BC,CA的中点分别是D,E,F,已知AB=8,AC=10,则四边形ADEF的周长是( )
A.8 B.9 C.10 D.18
5、(2020春 北仑区期末)如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
6、如图,四边形中,,,,点,分别为线段,上的动点(含端点,但点不与点重合),点,分别为,的中点,则长度的最大值为( )
A.8 B.7 C.6 D.5
7、如图,在平行四边形中,对角线交于点O,,E,F,G分别是 的中点,交于点H.下列结论:①;②;③;成立的个数有( )
A.3个 B.2个 C.1个 D.0个
8、(2019春 永康市期末)如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( )
A.7cm B.6cm C.5cm D.4cm
9、(2020春 婺城区校级月考)如图,在 ABCD中,∠A=45°,AD=,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A. B. C. D.1
10、如图,将△ABC沿AB边对折,使点C落在点D处,延长CA到E,使AE=AD,连接CD交AB于F,连接ED,则下列结论中:①若C△ABC=12,DE=5,则C四边形ABDE=17;②AB∥DE;
③∠CDE=90°;④S△ADE=2S△ADF,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
12、(2021·全国八年级专题练习)如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
13、如图,四边形中,,,若,,为的中点,
则的长为_______.
14、(2020·四川遂宁市·射洪中学九年级月考)如图,△ABC中,AD是中线,AE是角平分线, CF⊥AE于F,AB=13,AC=8,则DF的长为_________.
15、(2019春 下城区期末)如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点.连接EF,FM,则FM= ;线段EF的最大值为 .
16、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
17、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E在线段上且,点F是边的中点,若,,且,则的长是_______.
18、如图,已知,点A在边OX上,,过点A作于点C,以AC为一边在内作等边三角形ABC,点P是围成的区域(包括各边)内的一点,过点P作交OX于点D,作交OY于点E,则的最大值与最小值的积是______.
三、解答题
19、(2020春 临海市期末)如图,在 ABCD中,点F是边AB的中点,连接DF并延长交CB的延长线于点E.求证:EB=BC.
20、如图,在△ABC中,D是BC上一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
21、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E,点F分别是 的中点.连结 .
(1)求证:四边形是平行四边形.
(2)若平分,求平行四边形的周长.
22、(2019春 岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
23、在中,,E、F分别是、的中点,延长到点D,使,连接、、、,与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
24、(2020春 兰州期末)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=4,求DG的长度.
25、如图,在中有如下3个论断;①点是的边的中点;②点是边的中点;③.选择其中两个作为题设另一个为结论,可以写出所有以下三个命题,(1):①②③,(2):①③②,(3):②③①.
(1)正确的命题有______.(填番号)
(2)请对命题(2)的正误作出证明.
26、(2020 长春模拟)【感知】如图①,BD、CE分别是△ABC的外角平分线,过点A作AM⊥BD于M,AN⊥CE于N,连接MN,易证:MN=(AB+BC+AC)(不需要证明).
【探究】如图②,若BD、CE分别是△ABC的两个内角的平分线,且AM⊥BD于M,AN⊥CE于N,连接MN.试猜想MN与边AB、AC和BC之间的数量关系,并证明你的结论.
【应用】如图③,在四边形ABCD中,∠ABC=∠ADC=90°,射线BE平分∠ABC,AM⊥BE于点M,连接MD,延长BC至F,若∠DCF=∠ACD=75°,AB=2,直接写出MD的长度.
专题练:平行四边形与中位线
-2021-2022学年八年级数学下册(苏科版)(解析)
一、选择题
1、(2020春 湖州期末)如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( )
A.8cm B.5cm C.3cm D.2cm
【点拨】根据平行四边形的性质,可以得到AE=CE,AD=BC,再根据△ABE的周长比△BEC的周长小3cm,AB=5cm,即可得到BC的长,从而可以得到AD的长,本题得以解决.
【解析】解:∵四边形ABCD是平行四边形,
∴AE=CE,AD=BC,
∵△ABE的周长比△BEC的周长小3cm,
∴(BC+CE+BE)﹣(AB+AE+BE)=3,
∴BC﹣AB=3,
∵AB=5cm,
∴BC=8cm,
∴AD=8cm,
故选:A.
2、(2020春 长兴县期中)如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10 C.12 D.14
【点拨】根据线段中点的性质、三角形中位线定理得到BD=AB,BE=BC,DE=AC,计算即可.
【解析】解:∵点D、E分别是边AB、BC的中点,
∴BD=AB,BE=BC,DE=AC,
∴AB=2BD,BC=2BE,AC=2DE,
∴△ABC的周长=AB+BC+AC=2BD+2BE+2DE=2(BD+BE+DE)=2×△DBE的周长=2×7=14,
故选:D.
3、(2021 河南模拟)如图, ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5 B.2 C.2.5 D.3
【点拨】根据平行四边形的性质得出OA=3,OB=5,进而利用勾股定理得出AB的长,利用三角形中位线得出OE即可.
【解析】解:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴OA=3,OB=5,AB∥DC,
∵∠OCD=90°,
∴∠BAO=90°,
∴AB=,
∵E是BC边的中点,OA=OC,
∴2OE=AB,
∴OE=2,
故选:B.
4、如图,△ABC的边AB,BC,CA的中点分别是D,E,F,已知AB=8,AC=10,则四边形ADEF的周长是( )
A.8 B.9 C.10 D.18
【答案】D
【分析】本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
根据线段中点的概念求出AD、AF,根据三角形中位线定理求出DE、EF,计算即可.
【详解】解:∵△ABC的边AB、BC、CA的中点分别是D、E、F,
∴AD=AB=4,AF=AC=5,DE=AC=5,EF=AB=4,
∴四边形ADEF的周长=4+5+5+4=18,
故选:D.
5、(2020春 北仑区期末)如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
【点拨】此题考查了三角形的中位线定理,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
根据勾股定理得到AB=5,根据平行线的性质和角平分线的定义得到∠ABD=∠ADB,求得AB=AD=5,连接BF并延长交AD于G,根据全等三角形的性质得到BF=FG,AG=BC=3,求得DG=5﹣3=2,根据三角形中位线定理即可得到结论.
【解析】解:∵AC⊥BC,∴∠ACB=90°,
∵BC=3,AC=4,∴AB=5,
∵AD∥BC,∴∠ADB=∠DBC,
∵BD为∠ABC的平分线,∴∠ABD=∠CBD,
∴∠ABD=∠ADB,∴AB=AD=5,
连接BF并延长交AD于G,
∵AD∥BC,∴∠GAC=∠BCA,
∵F是AC的中点,∴AF=CF,
∵∠AFG=∠CFB,∴△AFG≌△CFB(AAS),
∴BF=FG,AG=BC=3,∴DG=5﹣3=2,
∵E是BD的中点,∴EF=DG=1.
故选:A.
6、如图,四边形中,,,,点,分别为线段,上的动点(含端点,但点不与点重合),点,分别为,的中点,则长度的最大值为( )
A.8 B.7 C.6 D.5
【分析】本题考查的是三角形中位线定理、勾股定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
连接DN,根据三角形中位线定理得到EF=DN,根据题意得到当点N与点B重合时,DN最大,根据勾股定理计算,得到答案.
【详解】
解:连接DN,
∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
7、如图,在平行四边形中,对角线交于点O,,E,F,G分别是 的中点,交于点H.下列结论:①;②;③;成立的个数有( )
A.3个 B.2个 C.1个 D.0个
【答案】A
【分析】本题考查了平行四边形性质和判定,三角形中位线定理,三角形面积,直角三角形斜边上中线等于斜边一半,等腰三角形性质等;熟练运用三角形中位线定理、等腰三角形“三线合一”、直角三角形斜边上中线等于斜边一半等性质是解题关键.
由平行四边形性质和等腰三角形“三线合一”即可得ED⊥CA,根据三角形中位线定理可得EF =AB;由直角三角形斜边上中线等于斜边一半可得EG=CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得EH=EG.
【详解】
解:如图,连接FG,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC,AD∥BC,AB=CD,AB∥CD,
∵BD=2AD,∴OD=AD,∵点E为OA中点,∴ED⊥CA,故①正确;
∵E,F,G分别是OA,OB,CD的中点,∴EF∥AB,EF=AB,
∵∠CED=90°,CG=DG=CD,∴EG=CD,∴EF=EG,故②正确;
∵EF∥CD,EF=DG,∴四边形DEFG是平行四边形,
∴EH=HG,即EH=EG,故③正确;
故选:A.
8、(2019春 永康市期末)如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( )
A.7cm B.6cm C.5cm D.4cm
【点拨】本题主要考查了平行四边形的性质以及三角形中位线定理的知识,解题的关键是证明出GH是△PEF的中位线,此题难度不大.
连接EF,先证明出四边形ABFE是平行四边形,再证明GH是△PEF的中位线,进而求出GH的长度.
【解析】解:连接EF,
∵四边形ABCD是平行四边形,∴AB=CD,AD=BD,AD∥BC,
∵E,F分别是AD,BC的中点,∴AE=BF,
∴四边形ABFE是平行四边形,∴AB=EF=10cm,
∵G,H分别是PE,PF的中点,∴GH是△PEF的中位线,
∴GH=EF=×10=5cm,
故选:C.
9、(2020春 婺城区校级月考)如图,在 ABCD中,∠A=45°,AD=,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A. B. C. D.1
【点拨】本题考查平行四边形的性质、三角形的中位线定理、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是确定EF的最小值,就是DM的最小值.
连接DM,利用三角形中位线定理,可知EF=DM,求出DM的最小值即可求出EF的最小值.
【解析】解:如图,连接DM,
∵E、F分别为DN、MN的中点,
∴EF=DM,
∴EF的最小值,就是DM的最小值,
当DM⊥AB时,DM最小,
Rt△ADM中,∠A=45°,AD=,
∴DM=AD=1,
∴EF=DM=,
∴EF的最小值是.
故选:A.
10、如图,将△ABC沿AB边对折,使点C落在点D处,延长CA到E,使AE=AD,连接CD交AB于F,连接ED,则下列结论中:①若C△ABC=12,DE=5,则C四边形ABDE=17;②AB∥DE;
③∠CDE=90°;④S△ADE=2S△ADF,正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】本题主要考查了图形的翻折,三角形的面积,平行线的判定和性质等知识点,熟练应用同位角相等两直线平行,内错角相等两直线平行,两直线平行同位角相等是解题的关键.
①由题知AE=AC,BD=BC,可得结论正确;
②由三角形外角知∠CAB+∠DAB=∠ADE+∠AED,又知∠CAB=∠DAB,∠ADE=∠AED,即可得∠CAB=∠DAB=∠ADE=∠AED,即可得证结论;
③由对称知CD⊥AB,由AB∥DE可得结论;
④由③知S△ADE=DF DE,S△ADF=DF AF,证AF是中位线可得AF=DE,即可得证结论.
【详解】
解:①由图形翻折可知,AD=AC,BD=BC,
∵AE=AD,∴AE=AC,∴C四边形ABDE=C△ABC+DE,
∵C△ABC=12,DE=5,∴C四边形ABDE=17,故①正确;
②由图形翻折知,∠CAB=∠DAB,
∵AE=AD,∴∠ADE=∠AED,
又∵∠CAB+∠DAB=∠ADE+∠AED,∴∠CAB=∠DAB=∠ADE=∠AED,∴AB∥DE,故②正确;
③由②知,AB∥DE,
由图形翻折知,CD⊥AB,∴∠CFA=∠CDE=90°,故③正确;
④由③知,∠CFA=∠CDE=90°,∴S△ADE=DF DE,S△ADF=DF AF,
∵AE=AC,AB∥DE,CF=DF,∴AF是△DEF的中位线,∴AF=DE,∴S△ADE=2S△ADF,故④正确,
故选:D.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
【答案】30
【分析】根据三角形的中位线性质,求出AC的长,再求出ΔABC的周长.
【详解】∵点 D 、 E 分别是 AB 、 BC 的中点,∴DE是ΔABC的中位线,∴ DE=AC ,
∵ DE=2.5 ,∴ AC=5 ,∵ AB=13 , BC=12 ,∴ C△ABC=AB+BC+AC=13+12+5=30.
故答案为:30.
12、(2021·全国八年级专题练习)如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
【答案】2
【分析】根据平行四边形的性质结合角平分线的定义可求解,即可得,利用等腰三角形的性质得到,进而可得是的中位线,根据三角形的中位线的性质可求解.
【详解】解:在平行四边形中,,∴,
∵平分,∴,∴,∴,
∵,∴,∵是的中点,∴是的中位线,∴
∵,∴;故答案为:2.
13、如图,四边形中,,,若,,为的中点,
则的长为_______.
【答案】
【分析】本题考查平行四边形的判定与性质、中位线的性质等知识,是重要考点,难度较易,掌握相关知识、作出正确的辅助线是解题关键.
延长,使,根据题意先证明四边形是平行四边形,可解得,继而得到是的中点,再结合中位线的性质解题即可.
【详解】解:延长,使,
四边形是平行四边形,∴DE=AB,
,
是的中点,
为的中点,
故答案为:.
14、(2020·四川遂宁市·射洪中学九年级月考)如图,△ABC中,AD是中线,AE是角平分线, CF⊥AE于F,AB=13,AC=8,则DF的长为_________.
【答案】2.5
【分析】延长CF交AB于H,证明△AFH≌△AFC,根据全等三角形的性质得到AH=AC=7,CF=FH,求出HB,根据三角形中位线定理计算即可.
【详解】解:延长CF交AB于H,
∵AE平分∠BAC,∴∠HAF=∠CAF,
在△AFH和△AFC中, ,
∴△AFH≌△AFC(ASA),∴AH=AC,CF=FH,
∵AB=13,AC=8,∴AH=AC=8,∴HB=AB-AH=13-8=5,
∵CF=FH,CD=DB,∴DF=HB=2.5,故答案为:2.5.
15、(2019春 下城区期末)如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点.连接EF,FM,则FM= ;线段EF的最大值为 .
【点拨】此题考查三角形中位线定理,关键是利用三角形的中位线平行于第三边,并且等于第三边的一半解答.
连接EM,利用三角形中位线定理解答即可.
【解析】解:连接EM,
∵E,F,M分别为边BC,AD和对角线BD的中点,
∴FM=,EM=,
当EF=EM+MF时,线段EF最大,即EF=1+3=4,
故答案为:1;4.
16、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
【答案】①④
【分析】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的性质等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.
根据全等三角形的判定与性质和平行四边形的判定与性质分别推理论证,即可得到结论.
【详解】解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,∴BF-OB=DE-OD,即OF=OE,∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,∴不能判定四边形AECF是平行四边形;
③∠EAB=∠FCO不能判定四边形AECF平行四边形;
④∵AF∥CE,∴∠AFB=∠CED,
在△ABF和△CDE中,,∴△ABF≌△CDE(AAS),∴BF=DE,
∴BF-OB=DE-OD,即OF=OE,
又∵OA=OC,∴四边形AECF是平行四边形;
故答案为:①④.
17、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E在线段上且,点F是边的中点,若,,且,则的长是_______.
【答案】
【分析】本题考查了平行四边形的判定与性质,三角形中位线定理,勾股定理,解决本题的关键是掌握平行四边形的判定与性质.
过点作于点,过点作交于点,连接,可得是等腰直角三角形,证明是三角形的中位线,可得四边形是平行四边形,再根据勾股定理即可得的长.
【详解】解:如图,过点作于点,过点作交于点,连接,
,是等腰直角三角形,,
,,,
,,是三角形的中位线,
,,,
点是边的中点,,,,
四边形是平行四边形,,
,,,,
,,,
,.
故答案为:.
18、如图,已知,点A在边OX上,,过点A作于点C,以AC为一边在内作等边三角形ABC,点P是围成的区域(包括各边)内的一点,过点P作交OX于点D,作交OY于点E,则的最大值与最小值的积是______.
【答案】40
【分析】
结合题意,得四边形ODPE是平行四边形,从而得到;结合点P是围成的区域(包括各边)内的一点,推导得当点P在AC上时,取最小值;当点P与点B重合时,取最大值;再分别根据两种情况,结合平行四边形、等边三角形、勾股定理的性质计算,即可完成求解.
【详解】
过点P做交于点H
∵∴
∵∴ ∴
∵,∴四边形ODPE是平行四边形
∴,∴
∴
∵点P是围成的区域(包括各边)内的一点
结合图形,得:当点P在AC上时,取最小值;当点P与点B重合时,取最大值;
当点P在AC上时,
∵,,∴,∴最小值;
当点P与点B重合时,如下图,AC和BD相交于点G
∴
∵,,
∴ , ,
∵等边三角形ABC,∴ ,
∴
∴ ,∴
∴GB是等边三角形ABC的角平分线,∴
又∵,即 ,∴是的中位线,∴
∴, ,∴
∵,∴ ,∴
∴,∴最大值
∴最大值与最小值的积
故答案为:40.
三、解答题
19、(2020春 临海市期末)如图,在 ABCD中,点F是边AB的中点,连接DF并延长交CB的延长线于点E.求证:EB=BC.
【点拨】本题考查了平行四边形性质,全等三角形的性质和判定,平行线的性质的应用,关键是推出△ADF≌△BEF.
根据平行四边形性质得出AD=BC,AD∥BC,推出∠A=∠FBE,∠ADF=∠E,证△ADF≌△BEF,推出BE=DA即可.
【解析】解:∵F是AB边的中点,
∴AF=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠A=∠FBE,∠ADF=∠E,
在△ADF和△BEF中,
∴△ADF≌△BEF(AAS),
∴AD=BE,
∵AD=BC,
∴EB=BC.
20、如图,在△ABC中,D是BC上一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
【分析】根据三角形的中位线定理可判定四边形EFGH为平行四边形,根据平行四边形的性质即可得到EG、HF互相平分.
【详解】连结EH、FG.,
∵E、H分别是BD、AD的中点,∴EH∥AB ,EH=AB.
同理,FG∥AB ,FG=AB.
∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形,∴EG、HF互相平分.
21、(20-21浙江杭州市十三中教育集团(总校)八下期中)如图所示,在平行四边形中,点E,点F分别是 的中点.连结 .
(1)求证:四边形是平行四边形.
(2)若平分,求平行四边形的周长.
【答案】(1)见解析;(2)18
【分析】(1)由平行四边形的性质和中点的性质可得DE=BF,即可得结论;
(2)由角平分线的性质和平行线的性质可证AB=AE=3,即可求解.
【详解】解:证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∵点E,点F分别是AD,BC的中点,
∴AE=DE=AD,BF=CF=BC,∴DE=BF,
又∵DE∥BF,∴四边形BEDF是平行四边形;
(2)∵BE平分∠ABC,∴∠ABE=∠EBC,
又∵AD∥BC,∴∠AEB=∠EBC,
∴∠ABE=∠AEB,∴AE=AB=3,∴AD=2AE=6,
∴平行四边形ABCD的周长=2×(3+6)=18.
22、(2019春 岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
【点拨】连接DE,FG,由BD与CE为中位线,利用中位线定理得到ED与BC平行,FG与BC平行,且都等于BC的一半,等量代换得到ED与FG平行且相等,进而得到四边形EFGD为平行四边形,利用平行四边形的性质即可得证.
【解析】证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
23、在中,,E、F分别是、的中点,延长到点D,使,连接、、、,与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
【答案】(1)理由见详解;(2)
【分析】本题主要考查三角形中位线、平行四边形的判定与性质及勾股定理,熟练掌握三角形中位线、平行四边形的判定与性质及勾股定理是解题的关键.
(1)由题意易得,,进而可得,则四边形是平行四边形,然后问题得证;
(2)由(1)可得,,,由勾股定理可得,进而可得,然后根据勾股定理可求解.
【详解】
解:(1)∵E、F分别是、的中点,∴,,
∵,∴
∴四边形是平行四边形,∴与互相平分;
(2)由(1)得:与互相平分,,,
∵,∴,,,
∵,∴,
∴,∴,
∴,∴.
24、(2020春 兰州期末)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=4,求DG的长度.
【点拨】本题考查了平行四边形的判定与性质、三角形中位线定理,解决本题的关键是综合运用平行四边形的判定与性质、三角形中位线定理.
(1)根据三角形中位线定理即可证明四边形DEFG是平行四边形;
(2)根据OB⊥OC,∠EOM和∠OCB互余,可以证明OM=MF,OM=EM,可得EF=2OM=8,由(1)有四边形DEFG是平行四边形,可得DG=EF=8.
【解析】解:(1)证明:∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,
同理EF∥BC,EF=BC,
∴DG=EF,DG∥EF,∴四边形DEFG是平行四边形;
(2)∵OB⊥OC∴∠BOC=90°,
∵∠EOM+∠COM=90°,∠EOM+∠OCB=90°,∴∠COM=∠OCB,
∵EF∥BC,∴∠OFE=∠OCB,∴∠MOF=∠MFO,∴OM=MF,
∵∠OEM+∠OFM=90°,∠EOM+∠MOF=90°
∴∠EOM=∠MEO,∴OM=EM,∴EF=2OM=8,
由(1)有四边形DEFG是平行四边形,∴DG=EF=8.
25、如图,在中有如下3个论断;①点是的边的中点;②点是边的中点;③.选择其中两个作为题设另一个为结论,可以写出所有以下三个命题,(1):①②③,(2):①③②,(3):②③①.
(1)正确的命题有______.(填番号)
(2)请对命题(2)的正误作出证明.
【答案】(1)(1)、(2)、(3);(2)证明见解析
【分析】本题考查中位线定理,解题的关键是掌握中位线定理的证明方法,通过构造全等三角形和平行四边形的性质和判断去证明中位线定理.
(1)这三个命题都是正确的,利用构造全等三角形的方法和平行四边形的性质和判定证明命题的正确性;
(2)延长至点,使,连接,证明,得到四边形为平行四边形,就可以证明结论.
【详解】
(1)命题(1):延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴,
∵为中点,∴,∴,
∴四边形为平行四边形,∴即;
命题(2):延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴即,
∵即,∴四边形为平行四边形,∴,
又∵,∴,∴点为的中点;
命题(3):延长线段至点,使得,
如下图:连接,
∵点为的中点,∴,
在中和中,,∴(SAS),
∴且,
由可得:,即,
又∵即,∴四边形为平行四边形,∴,
又∵,∴,则点为的中点;
(2)延长至点,使,连接,
∵点为中点,∴,
在和中,,∴(SAS),
∴且,∴即,
∵即,∴四边形为平行四边形,∴,
又∵,∴,∴点为的中点.
26、(2020 长春模拟)【感知】如图①,BD、CE分别是△ABC的外角平分线,过点A作AM⊥BD于M,AN⊥CE于N,连接MN,易证:MN=(AB+BC+AC)(不需要证明).
【探究】如图②,若BD、CE分别是△ABC的两个内角的平分线,且AM⊥BD于M,AN⊥CE于N,连接MN.试猜想MN与边AB、AC和BC之间的数量关系,并证明你的结论.
【应用】如图③,在四边形ABCD中,∠ABC=∠ADC=90°,射线BE平分∠ABC,AM⊥BE于点M,连接MD,延长BC至F,若∠DCF=∠ACD=75°,AB=2,直接写出MD的长度.
【点拨】本题考查四边形综合题,考查了等腰三角形的判定和性质,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,应用三角形中位线定理解决问题.
【感知】如图①,设AN的延长线交BC的延长线于K,AM的延长线交CB的延长线于J.利用三角形的中位线定理解决问题即可.
【探究】如图②,结论:MN=(AB+AC﹣BC).利用三角形的中位线定理解决问题即可.
【应用】如图③中,延长AM交BC于J,延长AD交BC的延长线于K.利用DM=(AC+BC﹣AC)求解即可.
【解析】解:【感知】如图①中,设AN的延长线交BC的延长线于K,AM的延长线交CB的延长线于J.
∵AM⊥BD,∴∠AMB=∠BMJ=90°,
∵∠ABM=∠JBM,∠ABM+∠BAM=90°,∠JBM+∠J=90°,
∴∠BAM=∠J,∴BA=BJ,同法可证:CA=CK,
∴AM=MJ,AN=NK,∴MN=JK=(JB+BC+CK)=(AB+BC+AC).
【探究】如图②中,结论:MN=(AB+AC﹣BC).
理由:延长AM交BC于F,延长AN交BC于G.
∵AM⊥BD,∴∠AMB=∠BMF=90°,
∵∠ABM=∠FBM,∠ABM+∠BAM=90°,∠FBM+∠BFM=90°,
∴∠BAM=∠BFM,∴BA=BF,同法可证:CA=CG,
∴AM=MF,AN=NG,∴MN=FG=(BF+CG﹣BC)=(AB+AC﹣BC).
【应用】如图③中,延长AM交BC于J,延长AD交BC的延长线于K.
由题意∠ACB=180°﹣∠ACD﹣∠DCF=30°,
∵∠ABC=90°,AB=2,∴AC=2AB=4,BC=AB=2,
同法可证DM=JK=(AC+BC﹣AB)=(4+2﹣2)=1+.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
