4.1 光的折射 同步练习题(Word版含答案)
文档属性
| 名称 | 4.1 光的折射 同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 772.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-04 16:25:10 | ||
图片预览


文档简介
4.1 光的折射
一、单选题
1.如图所示,边长为的正方体透明介质放在水平面上,在地面上离面距离为的点有一个光源,向透明介质的左侧面射出一束光,当此光线与水平面夹角为时,在面的折射光线刚好照射到点,则该透明介质对光的折射率为( )
A. B. C. D.
2.一束红光由空气射入玻璃,这束红光的( )
A.频率不变,波长变长 B.速度不变,波长变短
C.频率增高,波长变长 D.速度变慢,波长变短
3.一束光线从空气射向某种液体时,入射角为45°,反射光线和折射光线之间的夹角为105°,则光在该液体中的折射率为( )
A. B.2 C. D.
4.发出白光的细线光源(长度为)竖直放置,上端a恰好在水面以下,如图所示.现考虑线光源发出的靠近水面法线(图中的虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以表示红光所成的像的长度,以表示紫光所成的像的长度,则( )
A. B.
C. D.
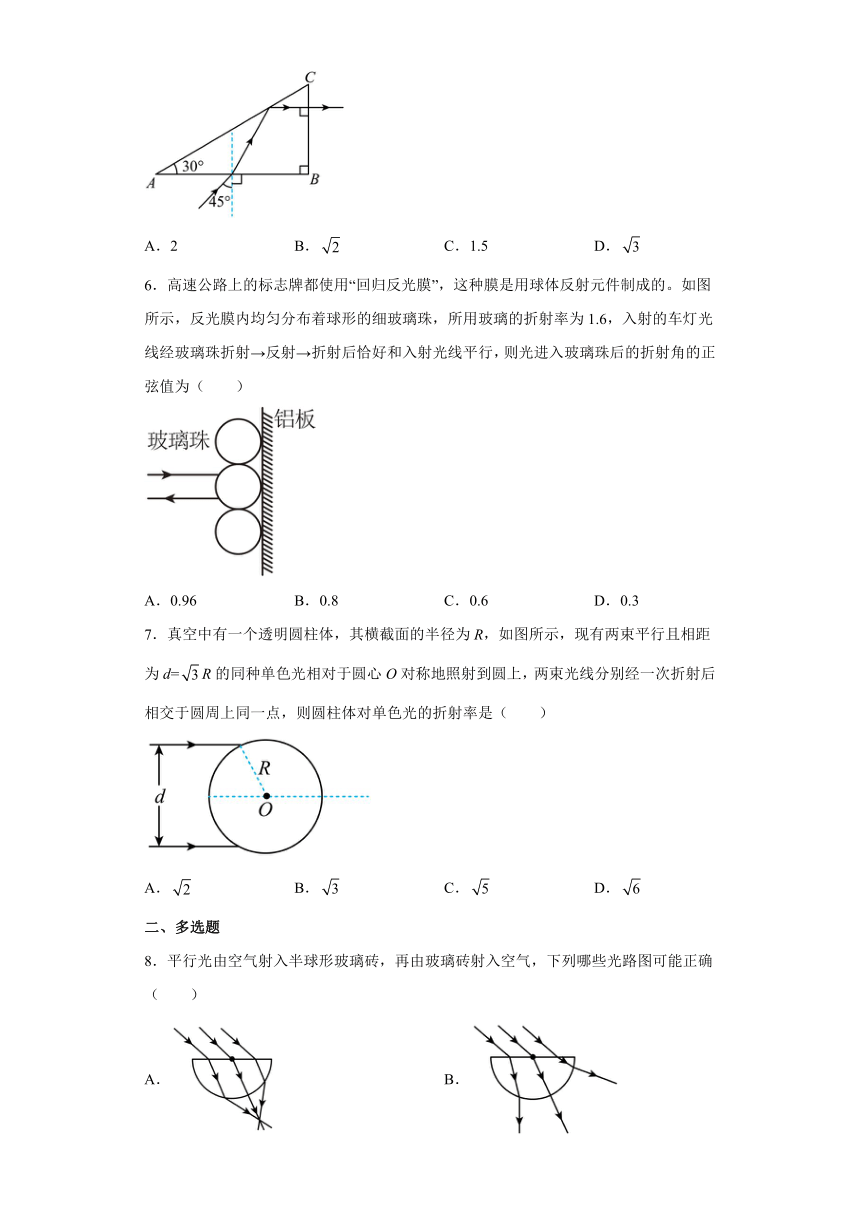
5.如图所示,在空气中有一直角棱镜,,一束单色光从边射入棱镜,入射角为,垂直于边射出,则该棱镜的折射率为( )
A.2 B. C.1.5 D.
6.高速公路上的标志牌都使用“回归反光膜”,这种膜是用球体反射元件制成的。如图所示,反光膜内均匀分布着球形的细玻璃珠,所用玻璃的折射率为1.6,入射的车灯光线经玻璃珠折射→反射→折射后恰好和入射光线平行,则光进入玻璃珠后的折射角的正弦值为( )
A.0.96 B.0.8 C.0.6 D.0.3
7.真空中有一个透明圆柱体,其横截面的半径为R,如图所示,现有两束平行且相距为d=R的同种单色光相对于圆心O对称地照射到圆上,两束光线分别经一次折射后相交于圆周上同一点,则圆柱体对单色光的折射率是( )
A. B. C. D.
二、多选题
8.平行光由空气射入半球形玻璃砖,再由玻璃砖射入空气,下列哪些光路图可能正确( )
A. B.
C. D.
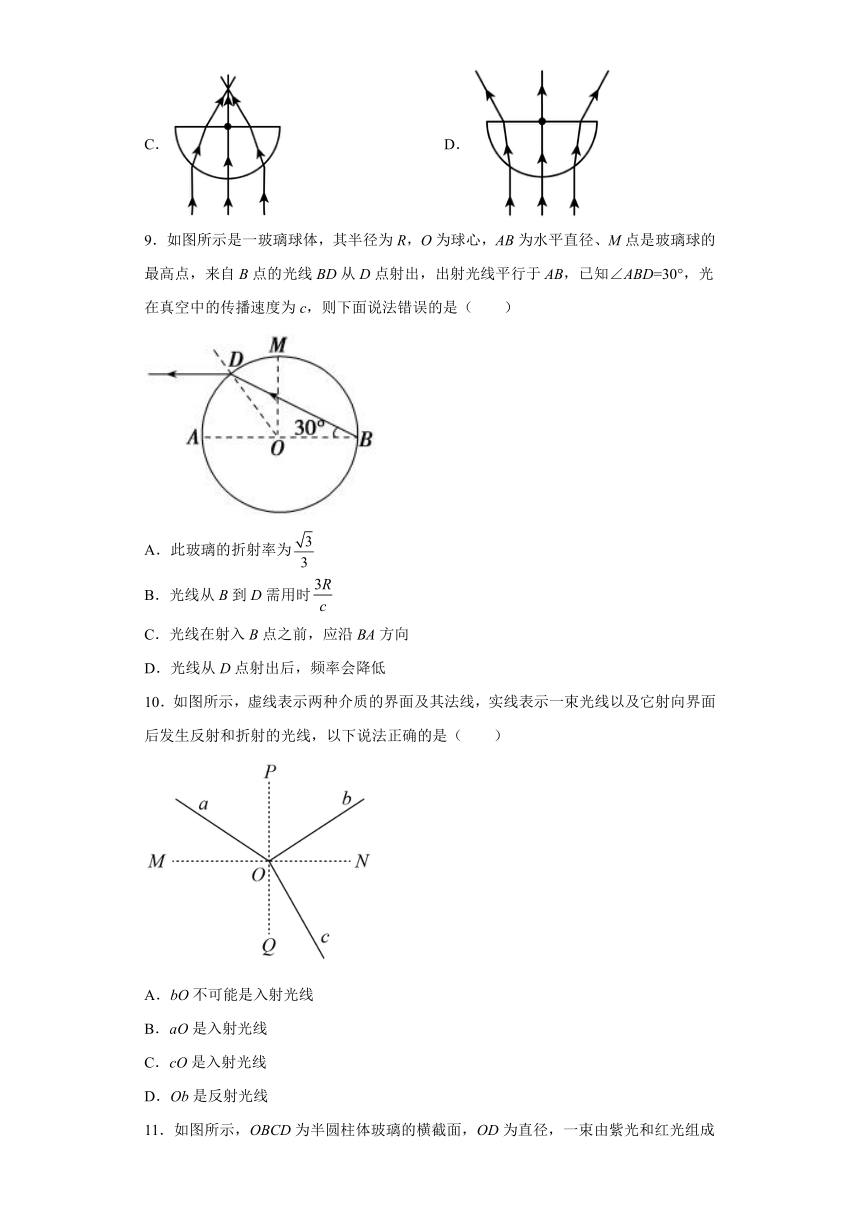
9.如图所示是一玻璃球体,其半径为R,O为球心,AB为水平直径、M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则下面说法错误的是( )
A.此玻璃的折射率为
B.光线从B到D需用时
C.光线在射入B点之前,应沿BA方向
D.光线从D点射出后,频率会降低
10.如图所示,虚线表示两种介质的界面及其法线,实线表示一束光线以及它射向界面后发生反射和折射的光线,以下说法正确的是( )
A.bO不可能是入射光线
B.aO是入射光线
C.cO是入射光线
D.Ob是反射光线
11.如图所示,OBCD为半圆柱体玻璃的横截面,OD为直径,一束由紫光和红光组成的复色光沿AO方向从真空射入玻璃分成OB、OC两束光。下列说法正确的是( )
A.光束OB是红光
B.紫光在真空中的波长比红光在真空中的波长小
C.紫光在玻璃中的频率比红光在玻璃中的频率小
D.两束光分别在OB、OC段传播时所用的时间相等
三、填空题
12.一束单色光从真空斜射向某种介质的表面,光路如图所示.由此可知介质的折射率等于___________.
13.如图所示,白光通过三棱镜后被分解为由红到紫按顺序排列的彩色光带(光谱),这种现象叫做光的色散.其原因是由于玻璃对各种色光的折射率不同.根据图我们可以得到:
①紫光的偏折角最大,红光的偏折角最小;
②由折射定律可以推理得:玻璃对紫光的折射率最________,对红光的折射率最________;
③根据光速与折射率的关系可以推理得:紫光在玻璃中的速度________,红光在玻璃中的光速最________.
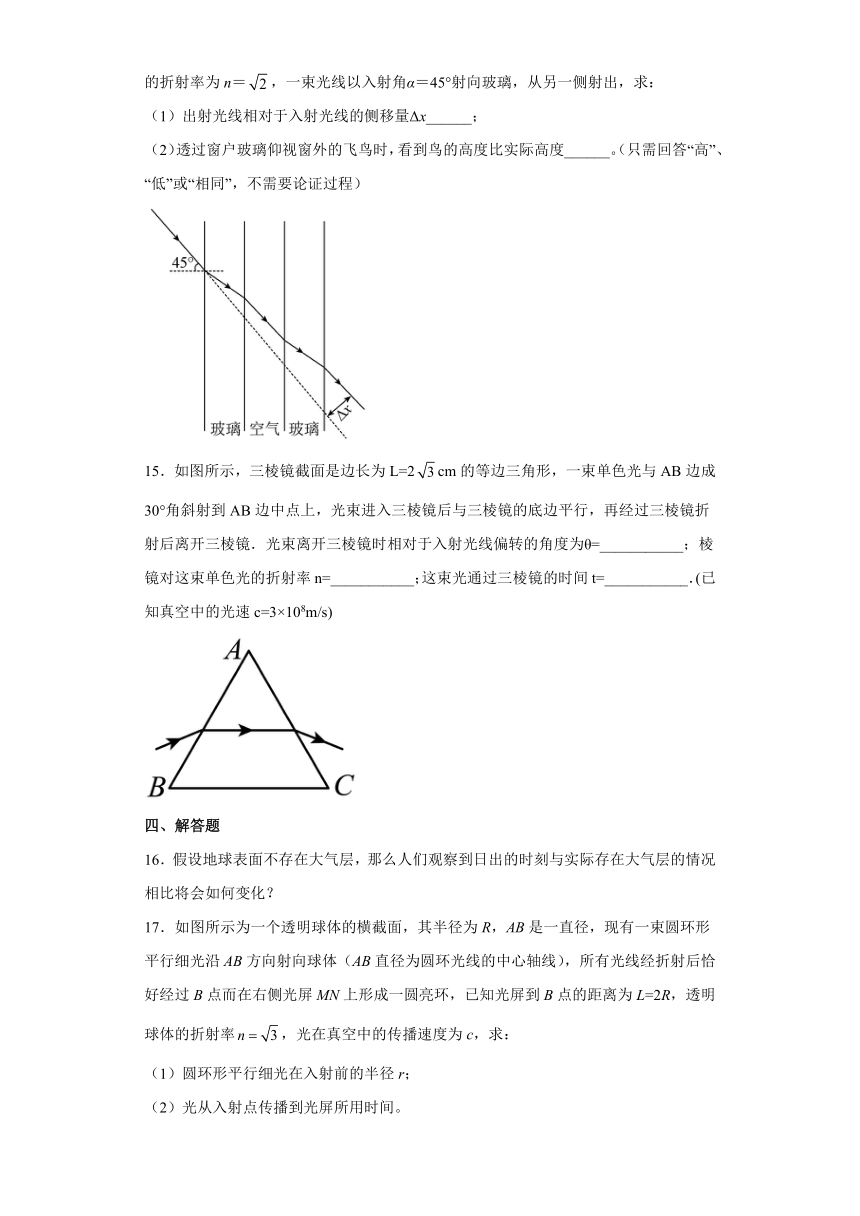
14.目前新建住宅为取得良好的保温效果,窗户广泛采用双层玻璃,如图所示,某双层玻璃由厚度均为d=0.5cm的单层玻璃组成,两玻璃板平行且中间有干燥的空气,玻璃的折射率为n=,一束光线以入射角α=45°射向玻璃,从另一侧射出,求:
(1)出射光线相对于入射光线的侧移量Δx______;
(2)透过窗户玻璃仰视窗外的飞鸟时,看到鸟的高度比实际高度______。(只需回答“高”、“低”或“相同”,不需要论证过程)
15.如图所示,三棱镜截面是边长为L=2cm的等边三角形,一束单色光与AB边成30°角斜射到AB边中点上,光束进入三棱镜后与三棱镜的底边平行,再经过三棱镜折射后离开三棱镜.光束离开三棱镜时相对于入射光线偏转的角度为θ=___________;棱镜对这束单色光的折射率n=___________;这束光通过三棱镜的时间t=___________.(已知真空中的光速c=3×108m/s)
四、解答题
16.假设地球表面不存在大气层,那么人们观察到日出的时刻与实际存在大气层的情况相比将会如何变化?
17.如图所示为一个透明球体的横截面,其半径为R,AB是一直径,现有一束圆环形平行细光沿AB方向射向球体(AB直径为圆环光线的中心轴线),所有光线经折射后恰好经过B点而在右侧光屏MN上形成一圆亮环,已知光屏到B点的距离为L=2R,透明球体的折射率,光在真空中的传播速度为c,求:
(1)圆环形平行细光在入射前的半径r;
(2)光从入射点传播到光屏所用时间。
18.如图所示,一个盛水容器内装有深度为H的水,激光笔发出一束激光射向水面O点,经折射后在水槽底部形成一光斑P。已知入射角,水的折射率,真空中光速为c,,。求:
(1)激光从O点传播到P点的时间t;
(2)打开出水口放水,当水面下降到原来一半深度时,光斑P仍然在容器底部,求光斑P移动的距离x。
19.如图,MN下方足够大的空间有一长方体玻璃,其折射率n=,玻璃的上边界MN是屏幕,玻璃中有一个正三棱柱的真空区域,三棱柱轴线与纸面垂直。图中竖直截面正三角形的边长为12 cm,顶点C紧靠屏幕,距离可忽略,底边AB与屏幕平行。一束激光在竖直截面内垂直于AB边射向AC边的中点O,结果在屏幕MN上出现了两个光斑,分布在C点的两侧。光在真空中的传播速度c=3×108 m/s。求:
(1)光在玻璃中的传播速度;(结果可以用根号表示)
(2)射到C点左侧的光斑离C点的距离。
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
ABCD.根据题意画出如光路图
设光在 AB面的入射点为E,由题意可知入射角
根据几何关系可知
故
设折射角为 r,根据几何关系有
因此折射率
故选C。
2.D
【解析】
【详解】
光在介质中传播,周期和频率由光源决定,所以红光的周期及频率保持不变,根据速度
玻璃的折射率大于空气,所以速度减小,波长
所以波长变短。
故选D。
3.C
【解析】
【详解】
由反射定律可知,反射角为45°,由几何关系可知,折射角为30°,故光在该液体中的折射率为
C正确。
故选C。
4.D
【解析】
【详解】
如图所示
由于紫光光折射率比红光大,故同一点发出的光经水面折射后,紫光比红光偏折角大,经反向延长后所成的虚像长度小即
故D正确,ABC错误。
故选D。
5.B
【解析】
【详解】
如图所示,由几何关系得,,由折射定律,则得该棱镜的折射率为
ACD错误,B正确。
故选B。
6.C
【解析】
【详解】
根据题意,画出光路图如图所示
根据几何关系可知
则根据折射率公式有
则
解得
故ABD错误C正确。
故选C。
7.B
【解析】
【详解】
光路图如图
由几何关系
故
又因为
故
所以折射率为
故选B。
8.AC
【解析】
【详解】
AB.当平行光射到玻璃砖的上表面时,入射角相同,则折射角一定相同且折射角小于入射角,即折射光线一定平行;从玻璃砖中进入空气时,折射角大于入射角,图A正确,B错误;
CD.当竖直向上的平行光射入玻璃砖时,折射角小于入射角,三条光线将汇聚;从玻璃砖上表面射出时再次汇聚,则图C正确,D错误。
故选AC。
9.ACD
【解析】
【详解】
A.如图
由几何知识得入射角
折射角
则此玻璃的折射率为
A错误,符合题意;
B.由几何知识得,BD长度
光在玻璃球内传播的速度
所以光线从B到D的时间为
B正确,不符合题意;
C.光线在射入B点之前,若应沿BA方向,则不可能在玻璃球内发生折射,C错误,符合题意;
D.光在传播过程中频率不变,D错误,符合题意。
故选ACD。
10.ABD
【解析】
【详解】
由于反射角等于入射角,反射光线、入射光线关于法线对称,所以aO、Ob可能是入射光线和反射光线,PQ是法线。又因为折射光线与入射光线分别位于法线两侧,所以aO是入射光线,Ob是反射光线,Oc是折射光线。
故选ABD。
11.BD
【解析】
【详解】
A.由于OB光偏折程度比OC光大,所以OB光的折射率大,可知,光束OB是紫光,OC是红光,故A错误;
B.由公式得
由于紫光的频率比红的大,则紫光在真空中的波长比红光在真空中的波长小,故B正确;
C.紫光在真空中的频率比红光在真空中的频率大,光束在真空中与在玻璃中频率相同,则紫光在玻璃中的频率比红光在玻璃中的频率大,故C错误;
D.光路图如图所示
设任一光线的入射角为i,折射角为r,光在玻璃中传播的路程是s,半圆柱的半径为R,则光在玻璃中的速度为,由几何知识得
则光在玻璃中传播时间为
由折射定律得,则
由题图知,两束光的入射角i相同,R、c相等,所以两束光分别在OB、OC段传播时所用的时间相等,故D正确。
故选BD。
12.
【解析】
【详解】
试题分析: 根据光的折射定律=.
考点:光的折射
13. 大 小 小 大
【解析】
【分析】
紫光的偏折角最大,红光的偏折角最小,玻璃对紫光的折射率最大,对红光的折射率最小,由公式分析光在玻璃砖中的速度大小.
【详解】
①由图知紫光的偏折角最大,红光的偏折角最小;
②由折射定律可以推理得:玻璃对紫光的折射率最大,对红光的折射率最小;
③根据光速与折射率的关系可以推理得:紫光在玻璃中的速度最小,红光在玻璃中的光速最大.
【点睛】
从光的色散实验发现可见光是复色光,知道在介质中,紫光的折射率最大,红光的折射率最小.紫光在玻璃中的速度最小,红光在玻璃中的光速最大
14. 0.30cm 高
【解析】
【分析】
【详解】
(1)由光的折射定律
知折射角的正弦值
sinr==
折射角
r=30°
由光路图中的几何关系,得
解得
Δx=0.30cm
(2)由光路可逆原理,可得射入房内的光线的反向延长线高于实际的光线。
15. 60° ,1×10-10s
【解析】
【详解】
解:如图所示,由于光束进入三棱镜后与三棱镜的底边平行,可知,折射率:;根据可得:,这束光通过三棱镜的时间:
16.将延后
【解析】
【详解】
若地球表面不存在大气层,太阳光将在真空中沿直线传播,由于地球是圆形的,所以只有太阳升到某一位置时才能观察到;而正因为地球表面上有大气层,太阳光射入大气层时会发生折射现象,能够提前观察到;所以如果地球表面不存在大气层,那么观察到的日出时刻与实际存在大气层时的情况相比将延后。
17.(1);(2)
【解析】
【详解】
(1)如图所示,设细光的入射角为,由几何关系可得
由折射定律可得
解得
圆环形平行细光在入射前的半径为
(2)光在介质中的传播速度为
光在介质中传播的时间为
光从B点进入空气中的折射角也为
光从B到MN的时间为
所以光从入射点传播到光屏所用时间为
18.(1);(2)
【解析】
【详解】
(1)根据折射定理
解得折射角大小
β=37°
光在水中的速度
激光从O点传播到P点的时间
(2)根据
由几何关系有:
x=h(tanα-tanβ)
当,代入数据解得
【点睛】
19.(1)×108 m/s;(2)6 cm
【解析】
【详解】
(1)光在玻璃中的传播速度
解得
(2)如图所示,在AC边,光的入射角i=60°
由光的折射定律
代入数据解得
r=30°
由几何关系可知△ODC为等边三角形,则
DC=OC=6 cm
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,边长为的正方体透明介质放在水平面上,在地面上离面距离为的点有一个光源,向透明介质的左侧面射出一束光,当此光线与水平面夹角为时,在面的折射光线刚好照射到点,则该透明介质对光的折射率为( )
A. B. C. D.
2.一束红光由空气射入玻璃,这束红光的( )
A.频率不变,波长变长 B.速度不变,波长变短
C.频率增高,波长变长 D.速度变慢,波长变短
3.一束光线从空气射向某种液体时,入射角为45°,反射光线和折射光线之间的夹角为105°,则光在该液体中的折射率为( )
A. B.2 C. D.
4.发出白光的细线光源(长度为)竖直放置,上端a恰好在水面以下,如图所示.现考虑线光源发出的靠近水面法线(图中的虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以表示红光所成的像的长度,以表示紫光所成的像的长度,则( )
A. B.
C. D.
5.如图所示,在空气中有一直角棱镜,,一束单色光从边射入棱镜,入射角为,垂直于边射出,则该棱镜的折射率为( )
A.2 B. C.1.5 D.
6.高速公路上的标志牌都使用“回归反光膜”,这种膜是用球体反射元件制成的。如图所示,反光膜内均匀分布着球形的细玻璃珠,所用玻璃的折射率为1.6,入射的车灯光线经玻璃珠折射→反射→折射后恰好和入射光线平行,则光进入玻璃珠后的折射角的正弦值为( )
A.0.96 B.0.8 C.0.6 D.0.3
7.真空中有一个透明圆柱体,其横截面的半径为R,如图所示,现有两束平行且相距为d=R的同种单色光相对于圆心O对称地照射到圆上,两束光线分别经一次折射后相交于圆周上同一点,则圆柱体对单色光的折射率是( )
A. B. C. D.
二、多选题
8.平行光由空气射入半球形玻璃砖,再由玻璃砖射入空气,下列哪些光路图可能正确( )
A. B.
C. D.
9.如图所示是一玻璃球体,其半径为R,O为球心,AB为水平直径、M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则下面说法错误的是( )
A.此玻璃的折射率为
B.光线从B到D需用时
C.光线在射入B点之前,应沿BA方向
D.光线从D点射出后,频率会降低
10.如图所示,虚线表示两种介质的界面及其法线,实线表示一束光线以及它射向界面后发生反射和折射的光线,以下说法正确的是( )
A.bO不可能是入射光线
B.aO是入射光线
C.cO是入射光线
D.Ob是反射光线
11.如图所示,OBCD为半圆柱体玻璃的横截面,OD为直径,一束由紫光和红光组成的复色光沿AO方向从真空射入玻璃分成OB、OC两束光。下列说法正确的是( )
A.光束OB是红光
B.紫光在真空中的波长比红光在真空中的波长小
C.紫光在玻璃中的频率比红光在玻璃中的频率小
D.两束光分别在OB、OC段传播时所用的时间相等
三、填空题
12.一束单色光从真空斜射向某种介质的表面,光路如图所示.由此可知介质的折射率等于___________.
13.如图所示,白光通过三棱镜后被分解为由红到紫按顺序排列的彩色光带(光谱),这种现象叫做光的色散.其原因是由于玻璃对各种色光的折射率不同.根据图我们可以得到:
①紫光的偏折角最大,红光的偏折角最小;
②由折射定律可以推理得:玻璃对紫光的折射率最________,对红光的折射率最________;
③根据光速与折射率的关系可以推理得:紫光在玻璃中的速度________,红光在玻璃中的光速最________.
14.目前新建住宅为取得良好的保温效果,窗户广泛采用双层玻璃,如图所示,某双层玻璃由厚度均为d=0.5cm的单层玻璃组成,两玻璃板平行且中间有干燥的空气,玻璃的折射率为n=,一束光线以入射角α=45°射向玻璃,从另一侧射出,求:
(1)出射光线相对于入射光线的侧移量Δx______;
(2)透过窗户玻璃仰视窗外的飞鸟时,看到鸟的高度比实际高度______。(只需回答“高”、“低”或“相同”,不需要论证过程)
15.如图所示,三棱镜截面是边长为L=2cm的等边三角形,一束单色光与AB边成30°角斜射到AB边中点上,光束进入三棱镜后与三棱镜的底边平行,再经过三棱镜折射后离开三棱镜.光束离开三棱镜时相对于入射光线偏转的角度为θ=___________;棱镜对这束单色光的折射率n=___________;这束光通过三棱镜的时间t=___________.(已知真空中的光速c=3×108m/s)
四、解答题
16.假设地球表面不存在大气层,那么人们观察到日出的时刻与实际存在大气层的情况相比将会如何变化?
17.如图所示为一个透明球体的横截面,其半径为R,AB是一直径,现有一束圆环形平行细光沿AB方向射向球体(AB直径为圆环光线的中心轴线),所有光线经折射后恰好经过B点而在右侧光屏MN上形成一圆亮环,已知光屏到B点的距离为L=2R,透明球体的折射率,光在真空中的传播速度为c,求:
(1)圆环形平行细光在入射前的半径r;
(2)光从入射点传播到光屏所用时间。
18.如图所示,一个盛水容器内装有深度为H的水,激光笔发出一束激光射向水面O点,经折射后在水槽底部形成一光斑P。已知入射角,水的折射率,真空中光速为c,,。求:
(1)激光从O点传播到P点的时间t;
(2)打开出水口放水,当水面下降到原来一半深度时,光斑P仍然在容器底部,求光斑P移动的距离x。
19.如图,MN下方足够大的空间有一长方体玻璃,其折射率n=,玻璃的上边界MN是屏幕,玻璃中有一个正三棱柱的真空区域,三棱柱轴线与纸面垂直。图中竖直截面正三角形的边长为12 cm,顶点C紧靠屏幕,距离可忽略,底边AB与屏幕平行。一束激光在竖直截面内垂直于AB边射向AC边的中点O,结果在屏幕MN上出现了两个光斑,分布在C点的两侧。光在真空中的传播速度c=3×108 m/s。求:
(1)光在玻璃中的传播速度;(结果可以用根号表示)
(2)射到C点左侧的光斑离C点的距离。
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
ABCD.根据题意画出如光路图
设光在 AB面的入射点为E,由题意可知入射角
根据几何关系可知
故
设折射角为 r,根据几何关系有
因此折射率
故选C。
2.D
【解析】
【详解】
光在介质中传播,周期和频率由光源决定,所以红光的周期及频率保持不变,根据速度
玻璃的折射率大于空气,所以速度减小,波长
所以波长变短。
故选D。
3.C
【解析】
【详解】
由反射定律可知,反射角为45°,由几何关系可知,折射角为30°,故光在该液体中的折射率为
C正确。
故选C。
4.D
【解析】
【详解】
如图所示
由于紫光光折射率比红光大,故同一点发出的光经水面折射后,紫光比红光偏折角大,经反向延长后所成的虚像长度小即
故D正确,ABC错误。
故选D。
5.B
【解析】
【详解】
如图所示,由几何关系得,,由折射定律,则得该棱镜的折射率为
ACD错误,B正确。
故选B。
6.C
【解析】
【详解】
根据题意,画出光路图如图所示
根据几何关系可知
则根据折射率公式有
则
解得
故ABD错误C正确。
故选C。
7.B
【解析】
【详解】
光路图如图
由几何关系
故
又因为
故
所以折射率为
故选B。
8.AC
【解析】
【详解】
AB.当平行光射到玻璃砖的上表面时,入射角相同,则折射角一定相同且折射角小于入射角,即折射光线一定平行;从玻璃砖中进入空气时,折射角大于入射角,图A正确,B错误;
CD.当竖直向上的平行光射入玻璃砖时,折射角小于入射角,三条光线将汇聚;从玻璃砖上表面射出时再次汇聚,则图C正确,D错误。
故选AC。
9.ACD
【解析】
【详解】
A.如图
由几何知识得入射角
折射角
则此玻璃的折射率为
A错误,符合题意;
B.由几何知识得,BD长度
光在玻璃球内传播的速度
所以光线从B到D的时间为
B正确,不符合题意;
C.光线在射入B点之前,若应沿BA方向,则不可能在玻璃球内发生折射,C错误,符合题意;
D.光在传播过程中频率不变,D错误,符合题意。
故选ACD。
10.ABD
【解析】
【详解】
由于反射角等于入射角,反射光线、入射光线关于法线对称,所以aO、Ob可能是入射光线和反射光线,PQ是法线。又因为折射光线与入射光线分别位于法线两侧,所以aO是入射光线,Ob是反射光线,Oc是折射光线。
故选ABD。
11.BD
【解析】
【详解】
A.由于OB光偏折程度比OC光大,所以OB光的折射率大,可知,光束OB是紫光,OC是红光,故A错误;
B.由公式得
由于紫光的频率比红的大,则紫光在真空中的波长比红光在真空中的波长小,故B正确;
C.紫光在真空中的频率比红光在真空中的频率大,光束在真空中与在玻璃中频率相同,则紫光在玻璃中的频率比红光在玻璃中的频率大,故C错误;
D.光路图如图所示
设任一光线的入射角为i,折射角为r,光在玻璃中传播的路程是s,半圆柱的半径为R,则光在玻璃中的速度为,由几何知识得
则光在玻璃中传播时间为
由折射定律得,则
由题图知,两束光的入射角i相同,R、c相等,所以两束光分别在OB、OC段传播时所用的时间相等,故D正确。
故选BD。
12.
【解析】
【详解】
试题分析: 根据光的折射定律=.
考点:光的折射
13. 大 小 小 大
【解析】
【分析】
紫光的偏折角最大,红光的偏折角最小,玻璃对紫光的折射率最大,对红光的折射率最小,由公式分析光在玻璃砖中的速度大小.
【详解】
①由图知紫光的偏折角最大,红光的偏折角最小;
②由折射定律可以推理得:玻璃对紫光的折射率最大,对红光的折射率最小;
③根据光速与折射率的关系可以推理得:紫光在玻璃中的速度最小,红光在玻璃中的光速最大.
【点睛】
从光的色散实验发现可见光是复色光,知道在介质中,紫光的折射率最大,红光的折射率最小.紫光在玻璃中的速度最小,红光在玻璃中的光速最大
14. 0.30cm 高
【解析】
【分析】
【详解】
(1)由光的折射定律
知折射角的正弦值
sinr==
折射角
r=30°
由光路图中的几何关系,得
解得
Δx=0.30cm
(2)由光路可逆原理,可得射入房内的光线的反向延长线高于实际的光线。
15. 60° ,1×10-10s
【解析】
【详解】
解:如图所示,由于光束进入三棱镜后与三棱镜的底边平行,可知,折射率:;根据可得:,这束光通过三棱镜的时间:
16.将延后
【解析】
【详解】
若地球表面不存在大气层,太阳光将在真空中沿直线传播,由于地球是圆形的,所以只有太阳升到某一位置时才能观察到;而正因为地球表面上有大气层,太阳光射入大气层时会发生折射现象,能够提前观察到;所以如果地球表面不存在大气层,那么观察到的日出时刻与实际存在大气层时的情况相比将延后。
17.(1);(2)
【解析】
【详解】
(1)如图所示,设细光的入射角为,由几何关系可得
由折射定律可得
解得
圆环形平行细光在入射前的半径为
(2)光在介质中的传播速度为
光在介质中传播的时间为
光从B点进入空气中的折射角也为
光从B到MN的时间为
所以光从入射点传播到光屏所用时间为
18.(1);(2)
【解析】
【详解】
(1)根据折射定理
解得折射角大小
β=37°
光在水中的速度
激光从O点传播到P点的时间
(2)根据
由几何关系有:
x=h(tanα-tanβ)
当,代入数据解得
【点睛】
19.(1)×108 m/s;(2)6 cm
【解析】
【详解】
(1)光在玻璃中的传播速度
解得
(2)如图所示,在AC边,光的入射角i=60°
由光的折射定律
代入数据解得
r=30°
由几何关系可知△ODC为等边三角形,则
DC=OC=6 cm
答案第1页,共2页
答案第1页,共2页
