6.1 函数
图片预览





文档简介
课件15张PPT。第六章 一次函数一、函 数一、复习回顾
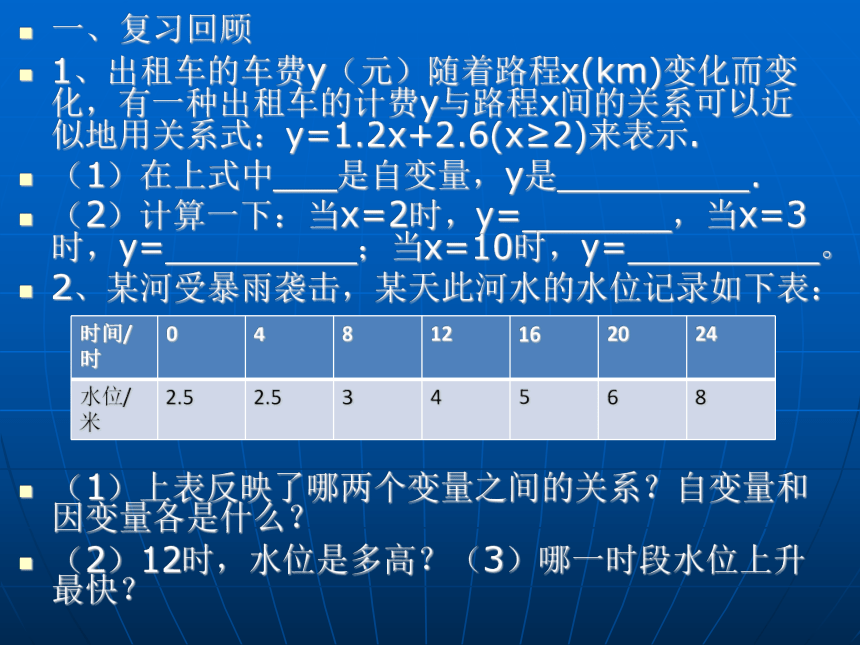
1、出租车的车费y(元)随着路程x(km)变化而变化,有一种出租车的计费y与路程x间的关系可以近似地用关系式:y=1.2x+2.6(x≥2)来表示.
(1)在上式中___是自变量,y是_________.
(2)计算一下:当x=2时,y=_______,当x=3时,y=_________;当x=10时,y=_________。
2、某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多高?(3)哪一时段水位上升最快?自主探究P98图6-1填写表格并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?
_______随着_____的变化而变化
3、对于给定的时间t,相应的高度h确定吗?
4、对于给定的每一个时间 t ,高度 h
对应有几个值?自主探究P99做一做1填写表格并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?
_______随着____的变化而变化
3、对于给定的每一个层数n ,总数y对应有几个值?
自主探究P99做一做2并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?___随着__的变化而变化
3、给定一个v值,你能求出相应的s值吗,计算当v分别为50,60,100时,相应的滑行距离s是多少?
4、对于给定的每一个速度v ,滑行距离 s 对应有几个值? 上面的三个问题中,有什么共同特点?一般的,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应的就确定一个y值,那么我们称y是x的函数(fun_ction),其中x是自变量,
y是因变量。列举生活中某个变化过程,看看其中
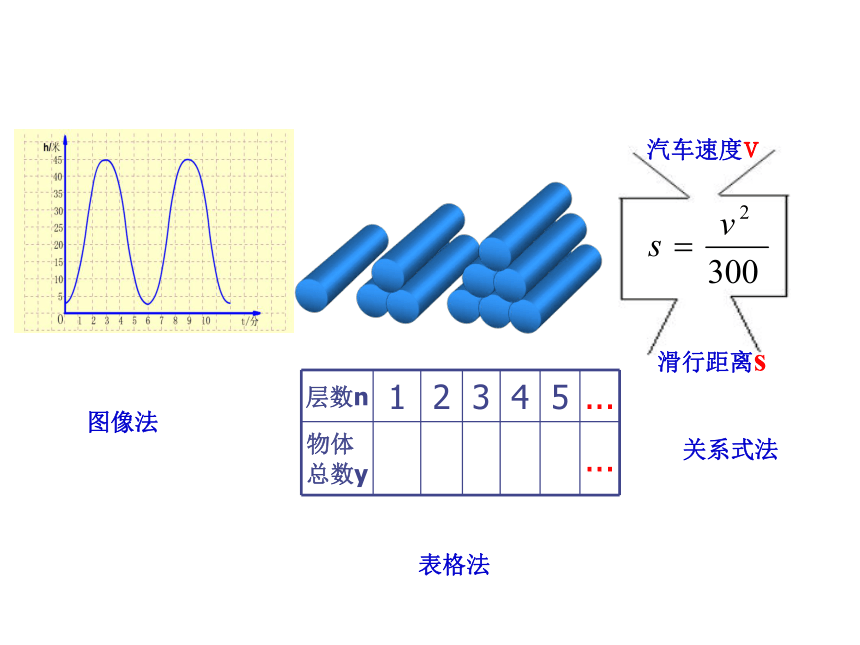
是否存在函数关系?只要用心,生活中处处有数学图像法表格法关系式法函数的表示方法:(1)图象法;
(2)表格法;
(3)关系式法。下面两幅图中,x都是自变量,则y是不是x的函数,为什么?例题1、下图中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若是,用了函数的哪种表示方法?图象法相信你能行练一练2、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?已知等腰三角形ABC的底边BC长为4,高AD的长x在变化,则△ABC的面积y=___,___是___的函数。 若正方形的边长为x,则面积y与边长x之间的关系是什么?y=x2xy是x的函数吗?y是x的函数你真行不断反思,感悟知识,
成就未来! 1、必做:配套练习册练习6.2 1-3 2、选做:配套练习册4(探索尝 试) 布置作业:三角形底边为8 cm,当它的高由小到大变化时,三角形的面积也随之发生了变化.
1.在这个变化过程中,自变量是____,因变量是___,___是___的函数。
2.如果三角形的高为h cm,面积S表示为_____。 谢谢,再见!
1、出租车的车费y(元)随着路程x(km)变化而变化,有一种出租车的计费y与路程x间的关系可以近似地用关系式:y=1.2x+2.6(x≥2)来表示.
(1)在上式中___是自变量,y是_________.
(2)计算一下:当x=2时,y=_______,当x=3时,y=_________;当x=10时,y=_________。
2、某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多高?(3)哪一时段水位上升最快?自主探究P98图6-1填写表格并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?
_______随着_____的变化而变化
3、对于给定的时间t,相应的高度h确定吗?
4、对于给定的每一个时间 t ,高度 h
对应有几个值?自主探究P99做一做1填写表格并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?
_______随着____的变化而变化
3、对于给定的每一个层数n ,总数y对应有几个值?
自主探究P99做一做2并完成下列问题
1、在这个变化过程中有几个变量?
2、自变量是什么?因变量是什么?___随着__的变化而变化
3、给定一个v值,你能求出相应的s值吗,计算当v分别为50,60,100时,相应的滑行距离s是多少?
4、对于给定的每一个速度v ,滑行距离 s 对应有几个值? 上面的三个问题中,有什么共同特点?一般的,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应的就确定一个y值,那么我们称y是x的函数(fun_ction),其中x是自变量,
y是因变量。列举生活中某个变化过程,看看其中
是否存在函数关系?只要用心,生活中处处有数学图像法表格法关系式法函数的表示方法:(1)图象法;
(2)表格法;
(3)关系式法。下面两幅图中,x都是自变量,则y是不是x的函数,为什么?例题1、下图中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若是,用了函数的哪种表示方法?图象法相信你能行练一练2、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?已知等腰三角形ABC的底边BC长为4,高AD的长x在变化,则△ABC的面积y=___,___是___的函数。 若正方形的边长为x,则面积y与边长x之间的关系是什么?y=x2xy是x的函数吗?y是x的函数你真行不断反思,感悟知识,
成就未来! 1、必做:配套练习册练习6.2 1-3 2、选做:配套练习册4(探索尝 试) 布置作业:三角形底边为8 cm,当它的高由小到大变化时,三角形的面积也随之发生了变化.
1.在这个变化过程中,自变量是____,因变量是___,___是___的函数。
2.如果三角形的高为h cm,面积S表示为_____。 谢谢,再见!
