苏科版七年级数学下册 10.1 二元一次方程 课件(共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 10.1 二元一次方程 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 470.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
10.1 二元一次方程
身边的数学!
甲
乙
2
5
6
7
8
1
3
4
1
3
2
5
8
4
6
7
甲
乙
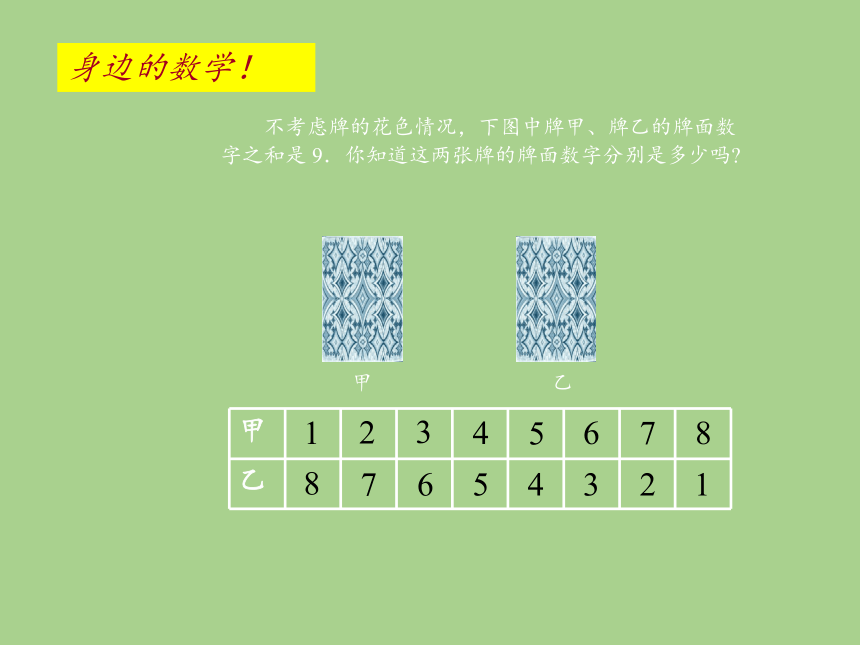
不考虑牌的花色情况,下图中牌甲、牌乙的牌面数字之和是 9.你知道这两张牌的牌面数字分别是多少吗
身边的数学!
设牌甲、牌乙的牌面数字分别是 x,y .
由题意得:
甲
乙
方程是表示生活中具有相等的数量关系的数学模型.
牌甲的牌面数字 牌乙的牌面数字 9
身边的数学!
解:设买钢笔 x 支,买笔记本 y 本.
用方程表示下列问题中的相等关系:
1.七年级(1)班为了奖励优秀学生,花 60 元购买钢笔和笔记本.已知每支钢笔 5元,每本笔记本 3 元,钢笔和笔记本分别买了多少
由题意得:
试一试:
用方程表示下列问题中的等量关系:
2.小明买了面值是 50 分的邮票和面值
是 80 分的邮票若干枚,共花了 6.3 元.小
明买了两种邮票各多少枚
由题意得:
解:设小明买了面值是 50 分的邮票 x 枚,面值是 80 分的邮票 y 枚.
试一试:
含有两个未知数,并且含有未知数的
项的次数都是 1 的方程叫做二元一次方程.
观察以上三个方程:它们有哪些共同的特点
探索(一)
判断下列方程是否为二元一次方程,并说
明理由.
含有三个未知数.
x 2 次数是 2.
x y 次数是 2.
√
√
不是整式方程.
口答:
不考虑牌的花色情况,设牌甲、牌乙的牌面数字分别是 x 与 y ,则由题意得:
甲
乙
满足方程 x + y = 9.
都是方程
x + y = 9 的解.
使方程两边相等的未知数的值叫做方程的解.
探索(二)
如 是方程 的一个解.
适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.
二元一次方程的一个解记作
探索(二)
若已知数甲和数乙分别是 x 与 y ,甲乙两数之和是 9,则由题意得: .
思考:这个方程的解是什么
…
探索(二)
思考:一个二元一次方程有多少个解?
一般地,一个二元一次方程有无数个解。
1.方程 2 x + 3 y +10= 35 有多少个解
你能分别给出一对正整数解、一对异号两数解、一对分数解吗
议一议:
(1)用含 x 的代数式表示 y ;
注意:也可用含 y 的代数式表示 x.
(2)任意取 x 的值代入,求出相应的 y 值;
(3)写出原方程的解.
2.如何求方程 2 x + 3 y +10= 35的解
议一议:
思考: 此时的二元一次方程 2x + 3 y+10 = 35仍有无数个解吗
某球员在一场篮球比赛中共得 35 分(其中罚球得 10 分).问:他分别投中了多少个两分球和三分球
根据下列语句,分别设适当的未知数,列出二元一次方程:
例题:
(1) 该球员最多投中了多少个三分球
(2) 该球员除罚球外最多投中了多少个球
(3) 如果该球员除罚球外投中了 10 个球,那么他投中的两分球、三分球各几个
2.根据所列的表格,回答下列问题:
1.请你设计一张表格,列出这名球员投中
的两分球和三分球的各种可能情况.
练一练:
设有2分的硬币x枚,5分的硬币y枚,硬币的总值为1元.
(1)可以列出方程:_________________;
(2)如果全是 2 分的硬币,共有多少枚
如果全是 5 分的硬币,共有多少枚
(3)用列表格的方式,列出2分和5分硬币枚数所有的可能情况.(课后完成)
2.用二元一次方程表达实际问题的关键是什么
1.谈谈“用二元一次方程表达实际问题”
与“用一元一次方程表达实际问题”的异同.
作业:完成课本P95,练一练1.2;
习题1.2.3.4
例: 甲种物品每个 4 kg,乙种物品每个7 kg.现有甲种物品 x 个,乙种物品 y 个,共 76 kg.
(1)列出关于 x、y 的二元一次方程;
(2)如果 x = 12,求 y 的值.
谢 谢
10.1 二元一次方程
身边的数学!
甲
乙
2
5
6
7
8
1
3
4
1
3
2
5
8
4
6
7
甲
乙
不考虑牌的花色情况,下图中牌甲、牌乙的牌面数字之和是 9.你知道这两张牌的牌面数字分别是多少吗
身边的数学!
设牌甲、牌乙的牌面数字分别是 x,y .
由题意得:
甲
乙
方程是表示生活中具有相等的数量关系的数学模型.
牌甲的牌面数字 牌乙的牌面数字 9
身边的数学!
解:设买钢笔 x 支,买笔记本 y 本.
用方程表示下列问题中的相等关系:
1.七年级(1)班为了奖励优秀学生,花 60 元购买钢笔和笔记本.已知每支钢笔 5元,每本笔记本 3 元,钢笔和笔记本分别买了多少
由题意得:
试一试:
用方程表示下列问题中的等量关系:
2.小明买了面值是 50 分的邮票和面值
是 80 分的邮票若干枚,共花了 6.3 元.小
明买了两种邮票各多少枚
由题意得:
解:设小明买了面值是 50 分的邮票 x 枚,面值是 80 分的邮票 y 枚.
试一试:
含有两个未知数,并且含有未知数的
项的次数都是 1 的方程叫做二元一次方程.
观察以上三个方程:它们有哪些共同的特点
探索(一)
判断下列方程是否为二元一次方程,并说
明理由.
含有三个未知数.
x 2 次数是 2.
x y 次数是 2.
√
√
不是整式方程.
口答:
不考虑牌的花色情况,设牌甲、牌乙的牌面数字分别是 x 与 y ,则由题意得:
甲
乙
满足方程 x + y = 9.
都是方程
x + y = 9 的解.
使方程两边相等的未知数的值叫做方程的解.
探索(二)
如 是方程 的一个解.
适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.
二元一次方程的一个解记作
探索(二)
若已知数甲和数乙分别是 x 与 y ,甲乙两数之和是 9,则由题意得: .
思考:这个方程的解是什么
…
探索(二)
思考:一个二元一次方程有多少个解?
一般地,一个二元一次方程有无数个解。
1.方程 2 x + 3 y +10= 35 有多少个解
你能分别给出一对正整数解、一对异号两数解、一对分数解吗
议一议:
(1)用含 x 的代数式表示 y ;
注意:也可用含 y 的代数式表示 x.
(2)任意取 x 的值代入,求出相应的 y 值;
(3)写出原方程的解.
2.如何求方程 2 x + 3 y +10= 35的解
议一议:
思考: 此时的二元一次方程 2x + 3 y+10 = 35仍有无数个解吗
某球员在一场篮球比赛中共得 35 分(其中罚球得 10 分).问:他分别投中了多少个两分球和三分球
根据下列语句,分别设适当的未知数,列出二元一次方程:
例题:
(1) 该球员最多投中了多少个三分球
(2) 该球员除罚球外最多投中了多少个球
(3) 如果该球员除罚球外投中了 10 个球,那么他投中的两分球、三分球各几个
2.根据所列的表格,回答下列问题:
1.请你设计一张表格,列出这名球员投中
的两分球和三分球的各种可能情况.
练一练:
设有2分的硬币x枚,5分的硬币y枚,硬币的总值为1元.
(1)可以列出方程:_________________;
(2)如果全是 2 分的硬币,共有多少枚
如果全是 5 分的硬币,共有多少枚
(3)用列表格的方式,列出2分和5分硬币枚数所有的可能情况.(课后完成)
2.用二元一次方程表达实际问题的关键是什么
1.谈谈“用二元一次方程表达实际问题”
与“用一元一次方程表达实际问题”的异同.
作业:完成课本P95,练一练1.2;
习题1.2.3.4
例: 甲种物品每个 4 kg,乙种物品每个7 kg.现有甲种物品 x 个,乙种物品 y 个,共 76 kg.
(1)列出关于 x、y 的二元一次方程;
(2)如果 x = 12,求 y 的值.
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
