人教版八年级下册数学一次函数实际应用题 专题训练(word版含解析)
文档属性
| 名称 | 人教版八年级下册数学一次函数实际应用题 专题训练(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 439.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览



文档简介
人教版八年级下册数学一次函数实际应用题专题训练
1.五一节快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元.
(1)分别表示出甲旅行社收费y1 和乙旅行社收费y2与旅游人数x的函数关系式;
(2)某单位有8至18人参加旅游(含8人和18人),问哪家旅行社的收费更优惠?
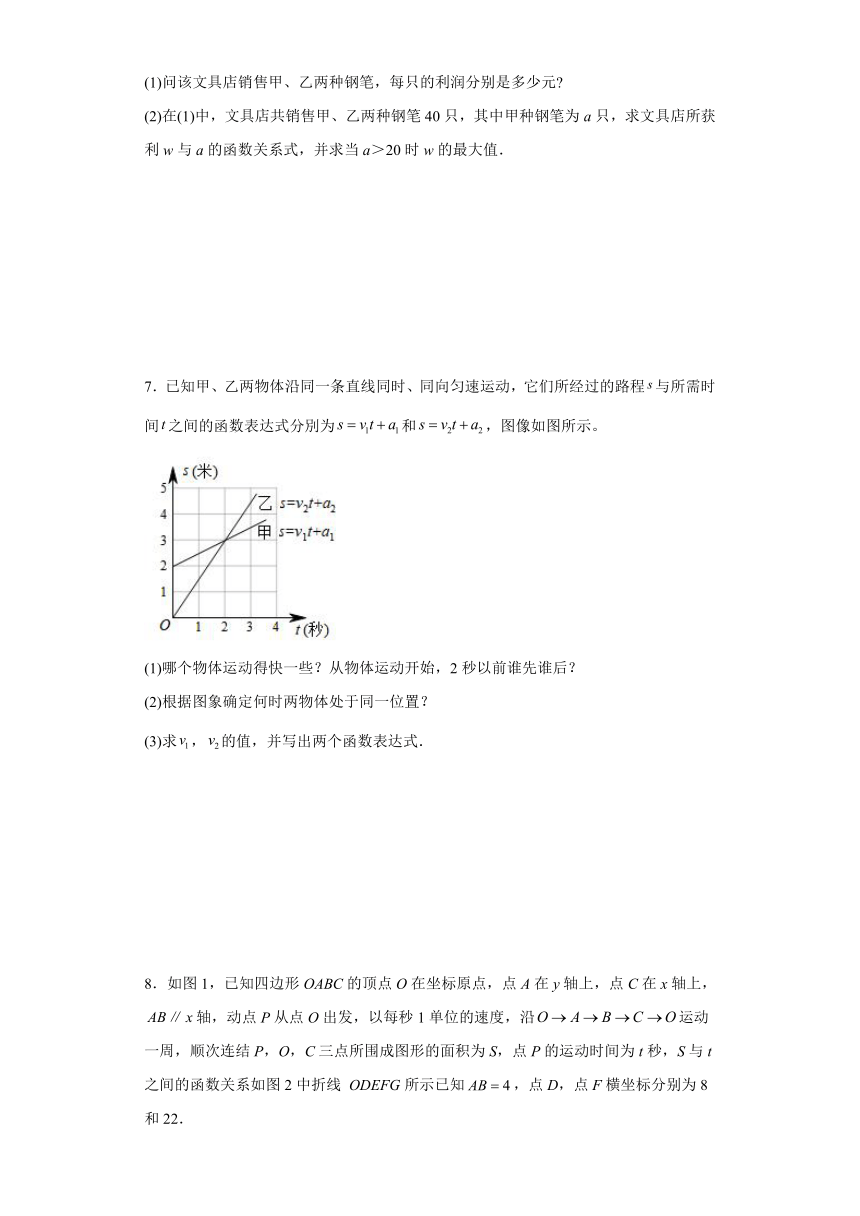
2.目前,全国各地都在积极开展新冠肺炎疫苗接种工作,某生物公司接到批量生产疫苗任务,要求5天内加工完成22万支疫苗,该公司安排甲,乙两车间共同完成加工任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止,设甲,乙两车间各自生产疫苗y(万支)与甲车间加工时间x(天)之间的关系如图1所示;两车间未生产疫苗w(万支)与甲车间加工时间x(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产疫苗 万支,第一天甲、乙两车间共生产疫苗 万支, ;
(2)当时,求甲、乙车间生产的疫苗数(万支)之差;
(3)若5.5万支疫苗恰好装满一辆货车,那么加工多长时间装满第一辆货车?再加工多长时间恰好装满第三辆货车?
3.某学校准备购买A、B两种型号的垃圾箱,通过市场调研发现:买2个A型垃圾箱和1个B型垃圾箱共需100元;买1个A型垃圾箱和2个B型垃圾箱共需110元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)若该校需购买A,B两种型号的垃圾箱共30个,其中A型垃圾箱不超过16个,求购买垃圾箱的总费用w(元)与A型垃圾箱的数量a(个)之间的函数关系式,并说明总费用至少要多少元?
4.济南某社区为倡导健康生活,推进全民健身,去年购进A,B两种健身器材若干件.经了解,B种健身器材的单价是A种健身器材的1.5倍,用6000元购买A种健身器材比用3600元购买B种健身器材多15件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共60件,且B种健身器材的数量不少于A种健身器材的4倍,请你确定一种购买方案使得购进A,B两种健身器材的费用最少.
5.某学校为进一步做好疫情防控工作,计划购进A,B两种口罩.已知每箱A种口罩比每箱B种口罩多10包,每箱A种口罩和每箱B种口罩的价格分别是630元和600元,而每包A种口罩和每包B种口罩的价格分别是这一批口罩平均每包价格的0.9倍和1.2倍.
(1)求这一批口罩平均每包的价格是多少元.
(2)如果购进A,B两种口罩共5500包,最多购进3500包A种口罩,为了使总费用最低,应购进A种口罩和B种口罩各多少包?总费用最低是多少元?
6.某文具店销售甲、乙两种钢笔,销售5只甲种、2只乙种钢笔,可获利润30元;销售2只甲种、1只乙种钢笔,可获利润13元.
(1)问该文具店销售甲、乙两种钢笔,每只的利润分别是多少元
(2)在(1)中,文具店共销售甲、乙两种钢笔40只,其中甲种钢笔为a只,求文具店所获利w与a的函数关系式,并求当a>20时w的最大值.
7.已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程与所需时间之间的函数表达式分別为和,图像如图所示。
(1)哪个物体运动得快一些?从物体运动开始,2秒以前谁先谁后?
(2)根据图象确定何时两物体处于同一位置?
(3)求,的值,并写出两个函数表达式.
8.如图1,已知四边形OABC的顶点O在坐标原点,点A在y轴上,点C在x轴上,轴,动点P从点O出发,以每秒1单位的速度,沿运动一周,顺次连结P,O,C三点所围成图形的面积为S,点P的运动时间为t秒,S与t之间的函数关系如图2中折线 ODEFG所示已知,点D,点F横坐标分别为8和22.
(1)求a和b的值.
(2)求直线EF的函数解析式.
(3)当P在BC上时,用t表示P点的纵坐标.
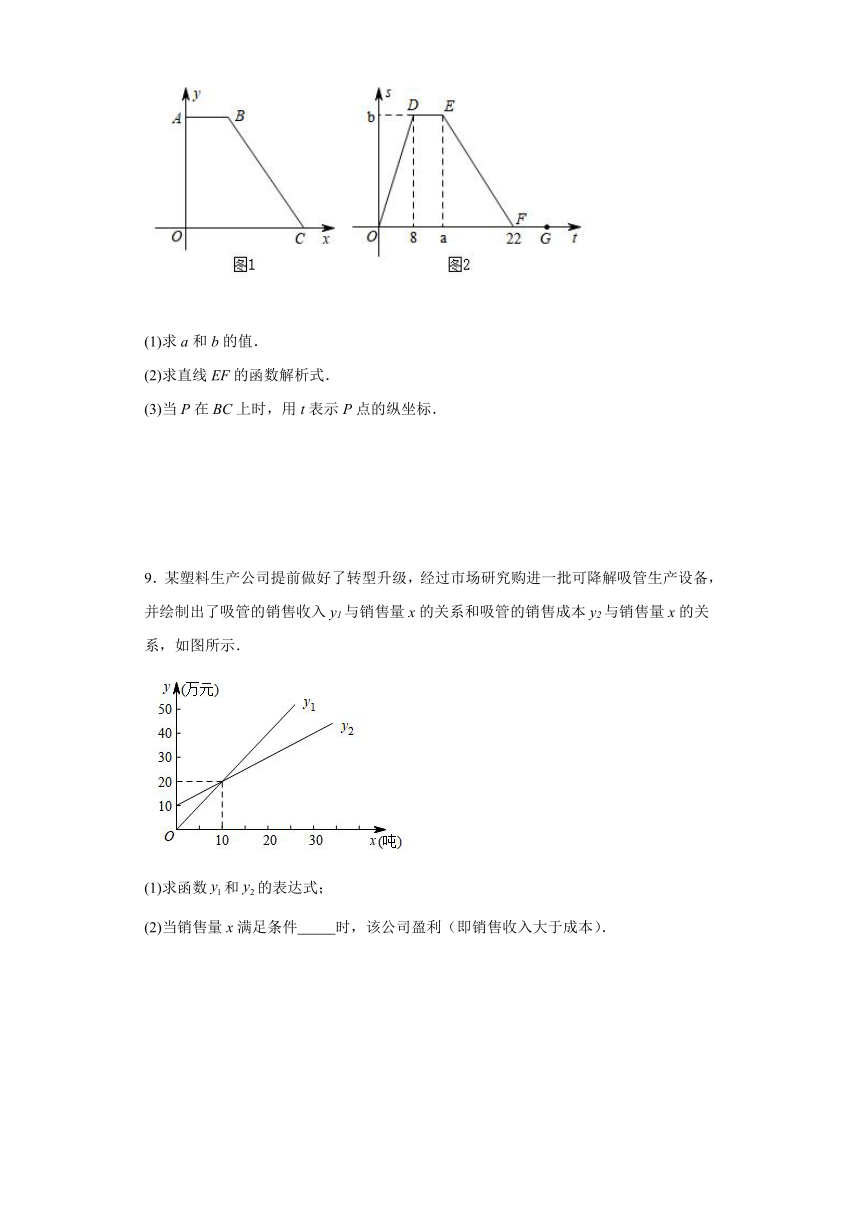
9.某塑料生产公司提前做好了转型升级,经过市场研究购进一批可降解吸管生产设备,并绘制出了吸管的销售收入y1与销售量x的关系和吸管的销售成本y2与销售量x的关系,如图所示.
(1)求函数和的表达式;
(2)当销售量x满足条件 时,该公司盈利(即销售收入大于成本).
10.某超市在冬至这天,购进了大量羊腿和羊排.顾客甲买了4斤羊腿,3斤羊排,一共花了272元;顾客乙买了2斤羊腿,1斤羊排,一共花了116元.
(1)羊腿和羊排的售价分别是每斤多少元?
(2)第二天进货时,超市老板根据前一天的销售情况,决定购进羊腿和羊排共180斤,且羊腿的重量不少于120斤,若在售价不变的情况下,每斤羊腿可盈利6元,而羊排的利润率为25%,问超市老板应该如何进货才能使得这批羊肉卖完时获利最大?最大利润是多少?
11.如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:
(1)求蜡烛在燃烧过程中高度与时间之间的函数表达式
(2)经过多少小时蜡烛燃烧完毕?
12.肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)直接写出A型桌椅每套 元,B型桌椅每套 元;
(2)若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.
①求y与x之间的函数关系,并直接写出x的取值范围;
②求出总费用最少的购置方案.
13.为了贯彻落实市委市政府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A,B两贫困村的计划.现决定从某地运送168箱小鸡到A,B两村养殖,若用大、小货车共18辆,则恰好能一次性运完这批小鸡,已知这两种大、小货车的载货能力分别为10箱/辆和8箱/辆,其运往A、B两村的运费如下表:
目的地车型 A村(元/辆) B村(元/辆)
大货车 80 90
小货车 40 60
(1)试求这18辆车中大、小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往4村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数表达式,并直接写出自变量取值范围;
(3)在(2)的条件下,若运往A村的小鸡不少于96箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
14.我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水吨,应交水费元.
(1)若,请写出与的函数关系式.
(2)若,请写出与的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
15.如图,在平面直角坐标系中,直线与直线相交于点.
(1)求m,b的值;
(2)求的面积;
(3)点P是x轴上的一点,过P作垂于x轴的直线与的交点分别为C,D,若P点的横坐标为n,当时直接写出n的取值范围.
16.经开区某中学计划举行一次知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.
(1)求甲、乙两种奖品的单价;
(2)根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品不少于乙种奖品的一半,应如何购买才能使总费用最少?并求出最少费用.
17.为加快“智慧校园”建设,某市准备为试点学校采购一批A、B两种型号的一体机.经过市场调查发现,今年每套B型一体机的价格比每套A型一体机的价格多0.6万元,且用960万元恰好能购买500套A型一体机和200套B型一体机.
(1)求今年每套A型、B型一体机的价格各是多少万元?
(2)该市明年计划采购A型、B型一体机共1100套,考虑物价因素,预计明年每套A型一体机的价格比今年上涨25%,若购买B型一体机的总费用不低于购买A型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
18.甲、乙两人相约周末登山,甲、乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)______米;
(2)求出甲距地面的高度与登山时间的关系式,并指出一次项系数的实际意义;
(3)若乙提速后,乙登山上升速度是甲登山上升速度的3倍,则在整个爬山过程中,登山多长时间时,甲乙两人距离地面的高度差为70米?
19.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为 km;
(2)两车经过 h相遇;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
20.已知A,B两地相距的路程为12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OCD和线段EF,分别表示甲、乙两人与A地的路程y甲、y乙与他们所行时间x(h)之间的函数关系,且OC与EF相交于点P.
(1)求y乙与x的函数关系式以及两人相遇地点P与A地的路程;
(2)求线段OC对应的y甲与x的函数关系式;
(3)求经过多少h,甲、乙两人相距的路程为6km.
试卷第1页,共3页
参考答案:
1.
(1)
x≤4时,y1=100x,
x>4时,y1=4×100+×100(x-4)=50x+200,
所以,y1=,
y2=0.7×100x=70x,
即y2=70x;
(2)
当y1 <y2 时,即 50x+200<70x ,解之得 x>10
∴超过10人,甲旅行社收费优惠.
当y1 =y2 时,即 50x+200=70x ,解之得 x=10
∴旅游的人数为10人,甲、乙旅行社收费一样.
当y1 >y2 时,即 50x+200>70x ,解之得 x<10,
∴旅游人数8(含8人)至10人但少于10人,乙旅行社收费优惠.
2.
解:由图1可得,车间每天生产疫苗:(万支);
由图2可得,甲、乙两车间第一天共生产疫苗:(万支);
;
故答案为:2,3.5 ,1.5.
(2)
解:由(1)可知甲车间生产疫苗数量y(万支)与x(天)之间的函系式为.
下面再求乙车间生产疫苗数量y(万支)与x(天)之间的函系式:
当时,;
当时,;
当时,设与x的函数关系式为,由题意可得,
解得,
即当时,y与x的函数关系式为,
当时,甲车间生产的疫苗数(万支)为(万支);
当时,乙车间生产的疫苗数(万支)为(万支)
∴甲、乙车间生产的疫苗数(万支)之差(万支).
(3)
解:由图2可得,
当时,生产的疫苗有(万支),
当时,每天生产的疫苗有:(万支),
∴加工第4天时,可以装满第三辆车,
故答案为:2天,2天.
答:加工2天时装满第一辆货车,再加工2天恰好装满第三辆货车.
3.
解:每个A型垃圾箱x元,B型垃圾箱y元,
根据题意,得,
(①+②)÷3得③,
①-③得x=30,
②-③得y=40,
∴;
(2)
解:∵A型垃圾箱的数量为a个,B型垃圾箱的数量为(30-a)个,
∴w=30a+40(30-a)=1200-10a,
∵k=-10<0,w随a的增大而减小,a≤16,
∴a=16时,购买垃圾箱的总费用w最小=1200-160=1040元.
4.
设A种健身器材的单价为x元,B种健身器材的单价为1.5x元,
根据题意得: ﹣ =15,
解得:x=240,
经检验x=240是原方程的解,且符合题意,
则1.5×240=360(元),
答:A,B两种健身器材的单价分别是240元,360元;
(2)
设购买A种型号健身器材m件,则购买B种型号的健身器材(60﹣m)件,总费用为y元,
根据题意得: ,
解得:0≤x≤12,
y=240m+360(60﹣m)=﹣120m+21600,
∵﹣120<0,
∴y随m的增大而减小,
∴当m取最大值12时,即购买A种器材12件,购买B种健身器材60﹣12=48件时y最小.
答:购买A种健身器材12件B种健身器材48件时费用最小.
5.
(1)
解:设这一批口罩平均每包的价格是x元,
根据题意得:,
解得x=20,
经检验,x=20是原方程的解,并符合题意,
答:这一批口罩平均每包的价格是20元;
(2)
解:由(1)可知,A种口罩每包价格为20×0.9=18(元),
B种口罩每包价格为20×1.2=24(元),
设购进A种口罩t包,这批口罩的总费用为w元,根据题意得:
w=18t+24(5500﹣t)=﹣6t+132000,
∵w是t的一次函数,k=﹣6<0,
∴w随t的增大而减小,
由∵t≤3500,
∴当t=3500时,w最小,
此时B种口罩有:5500﹣3500=2000(包),w=﹣6×3500+132000=111000,
答:购进A种口罩3500包,B种口罩2000包时,能使总费用最低,总费用最低是111000元.
6.
解:设每只甲种钢笔的利润为x元,每只乙种钢笔的利润为y元,
由题意可得:,
解得:,
答:每只甲种钢笔的利润为4元,每只乙种钢笔的利润为5元;
【小题2】
由题意可得,
w=4a+5(40-a)=-a+200,
∴w随a的增大而减小,
∵a>20且a为整数,
∴当a=21时,w取得最大值,此时w=179,
由上可得,文具店所获利w与a的函数关系式为w=-a+200,当a>20时w的最大值是179.
7
(1)
根据函数图象可知,乙物体运动得快一些,2秒前甲先乙后
(2)
根据函数图象可知,当时,,两个物体处于同一位置
(3)
根据函数图象可知,甲:当时,路程,则米/秒
乙:当时,路程,则米/秒
将分别代入
即
解得
将分别代入
即
解得
,,,
8.
解:如图,过点B作 轴于点M,
综合图 、图可知,OD段点P在线段OA上运动时,S与t之间的函数关系;DE段是点P在线段AB上运动时,S与t之间的函数关系;EF段是点P在线段BC上运动时,S与t之间的函数关系;
,动点P以每秒1单位的速度运动,
,
;
又OD段对应的时间是8s,EF段对应的时间为22s-12s=10s
,.
在中, 轴,,
,
,
;
;
,.
(2)
设直线EF的函数解析式为,
,,
E(12,40);
设直线EF的函数解析式为过E (12,40),F(22,0),
解得
直线EF的函数解析式
(3)
设点P的纵坐标为,如图4,
直线EF的函数解析式,
,
P点的纵坐标为.
9.
解:设y1与x的函数关系式为y1=kx,
∵点(10,20)在该函数图象上,
∴10k=20,得k=2,
即y1与x的函数关系式为y1=2x;
设y2与x的函数关系式为y2=cx+d,
,
解得,
即y2与x的函数关系式为y2=x+10;
(2)
解:由图象可得,
当x>10时,该公司盈利,
故答案为:x>10.
10.
设羊腿的售价每斤为a元,羊排的售价每斤为b元,
根据题意,得,
解得,
答:羊腿和羊排的售价分别是38元,40元;
(2)
每斤羊排的进价为:40÷(1+25%)=32(元),每斤羊排的利润为:32×25%=8(元),
设购进羊腿x斤,这批羊肉卖完时总获利为w元,
∵羊腿的重量不少于120斤,
∴x≥120,
w=6x+8(180-x)=-2x+1440,
∵-2<0,∴w随x的增大而减小,
∴当x=120时,w取得最大值,且w最大=-2×120+1440=1200,
此时180-120=60(斤).
答:超市老板应该购进120斤羊腿,60斤羊排,才能使得这批羊肉卖完时获利最大为1200元.
11.
由图象可知过(0,15),(1,7)两点,
设一次函数表达式为y=kx+b,
∴,
解得,
∴此一次函数表达式为:y=-8x+15(0≤x≤).
(2)
令y=0
∴-8x+15=0
解得:x=,
答:经过小时蜡烛燃烧完毕.
12.
解:设A型桌椅每套a元,B型桌椅每套b元,
根据题意,得:,
解得:,
所以A型桌椅每套600元,B型桌椅每套800元;
(2)
解:①据题意,总费用y=600x+800(20-x)+20×10=-200x+16200,
∵A型桌椅不少于12套,B型桌椅不少于6套,
∴,解得:12≤x≤14,
所以y与x之间的函数关系为y=-200x+16200(12≤x≤14,x为整数);
②由①知y=-200x+16200,且-200<0,
∴y随x的增大而减小,
∴当x=14时,总费用y最少,最少费用为-200×14+16200=13400元,
即购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元.
13.
设大货车用a辆,小货车用b辆,根据题意得:
解得:.
∴大货车用12辆,小货车用6辆.
(2)
设前往A村的大货车为x辆,则前往B村的大货车为(12- x)辆,前往A村的小货车为(10- x)辆,前往B村的小货车为[6-(10-x)]辆,
y=80x+90(12-x)+40(10-x)+60[6-(10-x)]=10x+1240.
4≤x≤12,且x为整数.
(4≤x≤12,且x为整数)
(3)
由题意得:10x+8(10-x)≥96,解得:x≥8,
又∵4≤x≤12,
∴8≤x≤12且为整数,
∵y=10x+1240,k=10>0,y随x的增大而增大,
∴当x=8时,y最小,
最小值为y=10×8+1240=1320(元).
答:使总运费最少的调配方案是:8辆大货车、2辆小货车前往A村;4辆大货车、4辆小货车前往B村.最少运费为1320元.
【点睛】
本题考查了二元一次方程组的应用,一次函数的应用,一元一次不等式组的应用,理解题意列出方程组、关系式、不等式是解题的关键.
14.(1)
(2)
(3)13吨
【解析】
【分析】
(1)当0<x≤8时,根据水费=用水量×1.5,即可求出y与x的函数关系式;
(2)当x>8时,根据“每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费”,得出水费=8×1.5+(用水量-8)×2.2,即可求出y与x的函数关系式;
(3)当0<x≤8时,y≤12,由此可知这个月该户用水量超过8吨,将y=23代入(2)中所求的关系式,求出x的值即可.
(1)
根据题意可知:
当时,;
(2)
根据题意可知:
当时,;
(3)
当时,,
的最大值为(元,,
该户当月用水超过8吨.
令中,则,
解得:.
答:这个月该户用了13吨水.
15.
解:∵点B(m,4)直线l2:y=2x上,
∴4=2m,
∴m=2,
∴点B(2,4),
将点B(2,4)代入直线得:,
解得b=3;
(2)
将y=0代入,得:x=-6,
∴A(-6,0),
∴OA=6,
∴△AOB的面积==12;
(3)
令x=n,则,,
当C、D在点B左侧时,
则,
解得:;
当C、D在点B右侧时,
则,
解得:;
综上:n的取值范围为或.
16.
设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,
依题意,得:,
解得,
答:甲种奖品的单价为20元/件,乙种奖品的单价为10元/件.
(2)
设购买甲种奖品m件,则购买乙种奖品(60-m)件,设购买两种奖品的总费用为w元,
∵甲种奖品的数量不少于乙种奖品数量的一半,
∴m≥(60-m),
∴m≥20.
依题意,得:w=20m+10(60-m)=10m+600,
∵10>0,
∴w随m值的增大而增大,
∴当学校购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.
17.
设今年每套A型一体机的价格为x万元,每套B型一体机的价格为y万元,
由题意得:,
解得:
答:今年每套A型一体机的价格为1.2万元,每套B型一体机的价格为1.8万元;
(2)
设该市明年购买A型一体机m套,则购买B型一体机(1100-m)套,
由题意可得:1.8(1100-m)≥1.2(1+25%)m,
解得:m≤600,
设明年需投入W万元,
W=1.2×(1+25%)m+1.8(1100-m)
=-0.3m+1980,
∵-0.3<0,
∴W随m的增大而减小,
∵m≤600,
∴当m=600时,W有最小值-0.3×600+1980=1800,
故该市明年至少需投入1800万元才能完成采购计划.
18.
解:由图象可得b=15÷1×2=30米,
故答案为:30.
(2)
解:设甲距地面的高度与登山时间的关系式y=kx+m,
由图象可得,过点C(0,100)、D(20,300),
∴,解得,
∴甲距地面的高度与登山时间的关系式y=10x+100;
一次项的系数是表示甲登山的速度;
(3)
解:甲登山速度为(300-100)÷20=10(米/分钟),
当0≤x≤2时,y=15x;当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0 x 20),
当10x+100 (30x 30)=70时,解得:x=3;
当30x 30 (10x+100)=70时,解得:x=10;
当300 (10x+100)=70时,解得:x=13.
∴登山3分钟、10分钟或13分钟时,甲乙两人距离地面的高度差为70米.
19.
(1)
根据图象,得
甲、乙两地之间的距为900km.
故答案为:900;
(2)
由函数图象,当慢车行驶4h时,慢车和快车相遇.
故答案为:4;
(3)
由题意,得
快车与慢车的速度和为:900÷4=225(km/h),
慢车的速度为:900÷12=75(km/h),
快车的速度为:225﹣75=150 (km/h).
答:快车的速度为150km/h,慢车的速度为75km/h;
(4)
由题意,得快车走完全程的时间按为:900÷150=6(h),
6h时两车之间的距离为:225×(6﹣4)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
,
解得:,
则y=225x﹣900,自变量x的取值范围是4≤x≤6.
20.
解:设y乙与x的函数关系式是,
∵点E(0,12),F(2,0)在函数y乙=kx+b的图象上,
∴ ,解得 ,
即y乙与x的函数关系式是,
当x=0.5时,,
即两人相遇地点P与A地的距离是9km;
(2)
解:设线段OC对应的y甲与x的函数关系式是y甲=ax,
∵点(0.5,9)在函数y甲=ax的图象上,
∴9=0.5a, 解得a=18,
即线段OP对应的y甲与x的函数关系式是y甲=18x;
(3)
解:①令 即
或
解得:或
甲从A地到达B地的时间为:小时,
经检验:不符合题意,舍去,
②当甲到达B地时,乙离B地6千米所走时间为:
(小时),
综上所述,经过小时或1小时,甲、乙两人相距6km.
答案第1页,共2页
1.五一节快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元.
(1)分别表示出甲旅行社收费y1 和乙旅行社收费y2与旅游人数x的函数关系式;
(2)某单位有8至18人参加旅游(含8人和18人),问哪家旅行社的收费更优惠?
2.目前,全国各地都在积极开展新冠肺炎疫苗接种工作,某生物公司接到批量生产疫苗任务,要求5天内加工完成22万支疫苗,该公司安排甲,乙两车间共同完成加工任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止,设甲,乙两车间各自生产疫苗y(万支)与甲车间加工时间x(天)之间的关系如图1所示;两车间未生产疫苗w(万支)与甲车间加工时间x(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产疫苗 万支,第一天甲、乙两车间共生产疫苗 万支, ;
(2)当时,求甲、乙车间生产的疫苗数(万支)之差;
(3)若5.5万支疫苗恰好装满一辆货车,那么加工多长时间装满第一辆货车?再加工多长时间恰好装满第三辆货车?
3.某学校准备购买A、B两种型号的垃圾箱,通过市场调研发现:买2个A型垃圾箱和1个B型垃圾箱共需100元;买1个A型垃圾箱和2个B型垃圾箱共需110元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)若该校需购买A,B两种型号的垃圾箱共30个,其中A型垃圾箱不超过16个,求购买垃圾箱的总费用w(元)与A型垃圾箱的数量a(个)之间的函数关系式,并说明总费用至少要多少元?
4.济南某社区为倡导健康生活,推进全民健身,去年购进A,B两种健身器材若干件.经了解,B种健身器材的单价是A种健身器材的1.5倍,用6000元购买A种健身器材比用3600元购买B种健身器材多15件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共60件,且B种健身器材的数量不少于A种健身器材的4倍,请你确定一种购买方案使得购进A,B两种健身器材的费用最少.
5.某学校为进一步做好疫情防控工作,计划购进A,B两种口罩.已知每箱A种口罩比每箱B种口罩多10包,每箱A种口罩和每箱B种口罩的价格分别是630元和600元,而每包A种口罩和每包B种口罩的价格分别是这一批口罩平均每包价格的0.9倍和1.2倍.
(1)求这一批口罩平均每包的价格是多少元.
(2)如果购进A,B两种口罩共5500包,最多购进3500包A种口罩,为了使总费用最低,应购进A种口罩和B种口罩各多少包?总费用最低是多少元?
6.某文具店销售甲、乙两种钢笔,销售5只甲种、2只乙种钢笔,可获利润30元;销售2只甲种、1只乙种钢笔,可获利润13元.
(1)问该文具店销售甲、乙两种钢笔,每只的利润分别是多少元
(2)在(1)中,文具店共销售甲、乙两种钢笔40只,其中甲种钢笔为a只,求文具店所获利w与a的函数关系式,并求当a>20时w的最大值.
7.已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程与所需时间之间的函数表达式分別为和,图像如图所示。
(1)哪个物体运动得快一些?从物体运动开始,2秒以前谁先谁后?
(2)根据图象确定何时两物体处于同一位置?
(3)求,的值,并写出两个函数表达式.
8.如图1,已知四边形OABC的顶点O在坐标原点,点A在y轴上,点C在x轴上,轴,动点P从点O出发,以每秒1单位的速度,沿运动一周,顺次连结P,O,C三点所围成图形的面积为S,点P的运动时间为t秒,S与t之间的函数关系如图2中折线 ODEFG所示已知,点D,点F横坐标分别为8和22.
(1)求a和b的值.
(2)求直线EF的函数解析式.
(3)当P在BC上时,用t表示P点的纵坐标.
9.某塑料生产公司提前做好了转型升级,经过市场研究购进一批可降解吸管生产设备,并绘制出了吸管的销售收入y1与销售量x的关系和吸管的销售成本y2与销售量x的关系,如图所示.
(1)求函数和的表达式;
(2)当销售量x满足条件 时,该公司盈利(即销售收入大于成本).
10.某超市在冬至这天,购进了大量羊腿和羊排.顾客甲买了4斤羊腿,3斤羊排,一共花了272元;顾客乙买了2斤羊腿,1斤羊排,一共花了116元.
(1)羊腿和羊排的售价分别是每斤多少元?
(2)第二天进货时,超市老板根据前一天的销售情况,决定购进羊腿和羊排共180斤,且羊腿的重量不少于120斤,若在售价不变的情况下,每斤羊腿可盈利6元,而羊排的利润率为25%,问超市老板应该如何进货才能使得这批羊肉卖完时获利最大?最大利润是多少?
11.如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:
(1)求蜡烛在燃烧过程中高度与时间之间的函数表达式
(2)经过多少小时蜡烛燃烧完毕?
12.肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)直接写出A型桌椅每套 元,B型桌椅每套 元;
(2)若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.
①求y与x之间的函数关系,并直接写出x的取值范围;
②求出总费用最少的购置方案.
13.为了贯彻落实市委市政府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A,B两贫困村的计划.现决定从某地运送168箱小鸡到A,B两村养殖,若用大、小货车共18辆,则恰好能一次性运完这批小鸡,已知这两种大、小货车的载货能力分别为10箱/辆和8箱/辆,其运往A、B两村的运费如下表:
目的地车型 A村(元/辆) B村(元/辆)
大货车 80 90
小货车 40 60
(1)试求这18辆车中大、小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往4村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数表达式,并直接写出自变量取值范围;
(3)在(2)的条件下,若运往A村的小鸡不少于96箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
14.我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水吨,应交水费元.
(1)若,请写出与的函数关系式.
(2)若,请写出与的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
15.如图,在平面直角坐标系中,直线与直线相交于点.
(1)求m,b的值;
(2)求的面积;
(3)点P是x轴上的一点,过P作垂于x轴的直线与的交点分别为C,D,若P点的横坐标为n,当时直接写出n的取值范围.
16.经开区某中学计划举行一次知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.
(1)求甲、乙两种奖品的单价;
(2)根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品不少于乙种奖品的一半,应如何购买才能使总费用最少?并求出最少费用.
17.为加快“智慧校园”建设,某市准备为试点学校采购一批A、B两种型号的一体机.经过市场调查发现,今年每套B型一体机的价格比每套A型一体机的价格多0.6万元,且用960万元恰好能购买500套A型一体机和200套B型一体机.
(1)求今年每套A型、B型一体机的价格各是多少万元?
(2)该市明年计划采购A型、B型一体机共1100套,考虑物价因素,预计明年每套A型一体机的价格比今年上涨25%,若购买B型一体机的总费用不低于购买A型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
18.甲、乙两人相约周末登山,甲、乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)______米;
(2)求出甲距地面的高度与登山时间的关系式,并指出一次项系数的实际意义;
(3)若乙提速后,乙登山上升速度是甲登山上升速度的3倍,则在整个爬山过程中,登山多长时间时,甲乙两人距离地面的高度差为70米?
19.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为 km;
(2)两车经过 h相遇;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
20.已知A,B两地相距的路程为12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OCD和线段EF,分别表示甲、乙两人与A地的路程y甲、y乙与他们所行时间x(h)之间的函数关系,且OC与EF相交于点P.
(1)求y乙与x的函数关系式以及两人相遇地点P与A地的路程;
(2)求线段OC对应的y甲与x的函数关系式;
(3)求经过多少h,甲、乙两人相距的路程为6km.
试卷第1页,共3页
参考答案:
1.
(1)
x≤4时,y1=100x,
x>4时,y1=4×100+×100(x-4)=50x+200,
所以,y1=,
y2=0.7×100x=70x,
即y2=70x;
(2)
当y1 <y2 时,即 50x+200<70x ,解之得 x>10
∴超过10人,甲旅行社收费优惠.
当y1 =y2 时,即 50x+200=70x ,解之得 x=10
∴旅游的人数为10人,甲、乙旅行社收费一样.
当y1 >y2 时,即 50x+200>70x ,解之得 x<10,
∴旅游人数8(含8人)至10人但少于10人,乙旅行社收费优惠.
2.
解:由图1可得,车间每天生产疫苗:(万支);
由图2可得,甲、乙两车间第一天共生产疫苗:(万支);
;
故答案为:2,3.5 ,1.5.
(2)
解:由(1)可知甲车间生产疫苗数量y(万支)与x(天)之间的函系式为.
下面再求乙车间生产疫苗数量y(万支)与x(天)之间的函系式:
当时,;
当时,;
当时,设与x的函数关系式为,由题意可得,
解得,
即当时,y与x的函数关系式为,
当时,甲车间生产的疫苗数(万支)为(万支);
当时,乙车间生产的疫苗数(万支)为(万支)
∴甲、乙车间生产的疫苗数(万支)之差(万支).
(3)
解:由图2可得,
当时,生产的疫苗有(万支),
当时,每天生产的疫苗有:(万支),
∴加工第4天时,可以装满第三辆车,
故答案为:2天,2天.
答:加工2天时装满第一辆货车,再加工2天恰好装满第三辆货车.
3.
解:每个A型垃圾箱x元,B型垃圾箱y元,
根据题意,得,
(①+②)÷3得③,
①-③得x=30,
②-③得y=40,
∴;
(2)
解:∵A型垃圾箱的数量为a个,B型垃圾箱的数量为(30-a)个,
∴w=30a+40(30-a)=1200-10a,
∵k=-10<0,w随a的增大而减小,a≤16,
∴a=16时,购买垃圾箱的总费用w最小=1200-160=1040元.
4.
设A种健身器材的单价为x元,B种健身器材的单价为1.5x元,
根据题意得: ﹣ =15,
解得:x=240,
经检验x=240是原方程的解,且符合题意,
则1.5×240=360(元),
答:A,B两种健身器材的单价分别是240元,360元;
(2)
设购买A种型号健身器材m件,则购买B种型号的健身器材(60﹣m)件,总费用为y元,
根据题意得: ,
解得:0≤x≤12,
y=240m+360(60﹣m)=﹣120m+21600,
∵﹣120<0,
∴y随m的增大而减小,
∴当m取最大值12时,即购买A种器材12件,购买B种健身器材60﹣12=48件时y最小.
答:购买A种健身器材12件B种健身器材48件时费用最小.
5.
(1)
解:设这一批口罩平均每包的价格是x元,
根据题意得:,
解得x=20,
经检验,x=20是原方程的解,并符合题意,
答:这一批口罩平均每包的价格是20元;
(2)
解:由(1)可知,A种口罩每包价格为20×0.9=18(元),
B种口罩每包价格为20×1.2=24(元),
设购进A种口罩t包,这批口罩的总费用为w元,根据题意得:
w=18t+24(5500﹣t)=﹣6t+132000,
∵w是t的一次函数,k=﹣6<0,
∴w随t的增大而减小,
由∵t≤3500,
∴当t=3500时,w最小,
此时B种口罩有:5500﹣3500=2000(包),w=﹣6×3500+132000=111000,
答:购进A种口罩3500包,B种口罩2000包时,能使总费用最低,总费用最低是111000元.
6.
解:设每只甲种钢笔的利润为x元,每只乙种钢笔的利润为y元,
由题意可得:,
解得:,
答:每只甲种钢笔的利润为4元,每只乙种钢笔的利润为5元;
【小题2】
由题意可得,
w=4a+5(40-a)=-a+200,
∴w随a的增大而减小,
∵a>20且a为整数,
∴当a=21时,w取得最大值,此时w=179,
由上可得,文具店所获利w与a的函数关系式为w=-a+200,当a>20时w的最大值是179.
7
(1)
根据函数图象可知,乙物体运动得快一些,2秒前甲先乙后
(2)
根据函数图象可知,当时,,两个物体处于同一位置
(3)
根据函数图象可知,甲:当时,路程,则米/秒
乙:当时,路程,则米/秒
将分别代入
即
解得
将分别代入
即
解得
,,,
8.
解:如图,过点B作 轴于点M,
综合图 、图可知,OD段点P在线段OA上运动时,S与t之间的函数关系;DE段是点P在线段AB上运动时,S与t之间的函数关系;EF段是点P在线段BC上运动时,S与t之间的函数关系;
,动点P以每秒1单位的速度运动,
,
;
又OD段对应的时间是8s,EF段对应的时间为22s-12s=10s
,.
在中, 轴,,
,
,
;
;
,.
(2)
设直线EF的函数解析式为,
,,
E(12,40);
设直线EF的函数解析式为过E (12,40),F(22,0),
解得
直线EF的函数解析式
(3)
设点P的纵坐标为,如图4,
直线EF的函数解析式,
,
P点的纵坐标为.
9.
解:设y1与x的函数关系式为y1=kx,
∵点(10,20)在该函数图象上,
∴10k=20,得k=2,
即y1与x的函数关系式为y1=2x;
设y2与x的函数关系式为y2=cx+d,
,
解得,
即y2与x的函数关系式为y2=x+10;
(2)
解:由图象可得,
当x>10时,该公司盈利,
故答案为:x>10.
10.
设羊腿的售价每斤为a元,羊排的售价每斤为b元,
根据题意,得,
解得,
答:羊腿和羊排的售价分别是38元,40元;
(2)
每斤羊排的进价为:40÷(1+25%)=32(元),每斤羊排的利润为:32×25%=8(元),
设购进羊腿x斤,这批羊肉卖完时总获利为w元,
∵羊腿的重量不少于120斤,
∴x≥120,
w=6x+8(180-x)=-2x+1440,
∵-2<0,∴w随x的增大而减小,
∴当x=120时,w取得最大值,且w最大=-2×120+1440=1200,
此时180-120=60(斤).
答:超市老板应该购进120斤羊腿,60斤羊排,才能使得这批羊肉卖完时获利最大为1200元.
11.
由图象可知过(0,15),(1,7)两点,
设一次函数表达式为y=kx+b,
∴,
解得,
∴此一次函数表达式为:y=-8x+15(0≤x≤).
(2)
令y=0
∴-8x+15=0
解得:x=,
答:经过小时蜡烛燃烧完毕.
12.
解:设A型桌椅每套a元,B型桌椅每套b元,
根据题意,得:,
解得:,
所以A型桌椅每套600元,B型桌椅每套800元;
(2)
解:①据题意,总费用y=600x+800(20-x)+20×10=-200x+16200,
∵A型桌椅不少于12套,B型桌椅不少于6套,
∴,解得:12≤x≤14,
所以y与x之间的函数关系为y=-200x+16200(12≤x≤14,x为整数);
②由①知y=-200x+16200,且-200<0,
∴y随x的增大而减小,
∴当x=14时,总费用y最少,最少费用为-200×14+16200=13400元,
即购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元.
13.
设大货车用a辆,小货车用b辆,根据题意得:
解得:.
∴大货车用12辆,小货车用6辆.
(2)
设前往A村的大货车为x辆,则前往B村的大货车为(12- x)辆,前往A村的小货车为(10- x)辆,前往B村的小货车为[6-(10-x)]辆,
y=80x+90(12-x)+40(10-x)+60[6-(10-x)]=10x+1240.
4≤x≤12,且x为整数.
(4≤x≤12,且x为整数)
(3)
由题意得:10x+8(10-x)≥96,解得:x≥8,
又∵4≤x≤12,
∴8≤x≤12且为整数,
∵y=10x+1240,k=10>0,y随x的增大而增大,
∴当x=8时,y最小,
最小值为y=10×8+1240=1320(元).
答:使总运费最少的调配方案是:8辆大货车、2辆小货车前往A村;4辆大货车、4辆小货车前往B村.最少运费为1320元.
【点睛】
本题考查了二元一次方程组的应用,一次函数的应用,一元一次不等式组的应用,理解题意列出方程组、关系式、不等式是解题的关键.
14.(1)
(2)
(3)13吨
【解析】
【分析】
(1)当0<x≤8时,根据水费=用水量×1.5,即可求出y与x的函数关系式;
(2)当x>8时,根据“每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费”,得出水费=8×1.5+(用水量-8)×2.2,即可求出y与x的函数关系式;
(3)当0<x≤8时,y≤12,由此可知这个月该户用水量超过8吨,将y=23代入(2)中所求的关系式,求出x的值即可.
(1)
根据题意可知:
当时,;
(2)
根据题意可知:
当时,;
(3)
当时,,
的最大值为(元,,
该户当月用水超过8吨.
令中,则,
解得:.
答:这个月该户用了13吨水.
15.
解:∵点B(m,4)直线l2:y=2x上,
∴4=2m,
∴m=2,
∴点B(2,4),
将点B(2,4)代入直线得:,
解得b=3;
(2)
将y=0代入,得:x=-6,
∴A(-6,0),
∴OA=6,
∴△AOB的面积==12;
(3)
令x=n,则,,
当C、D在点B左侧时,
则,
解得:;
当C、D在点B右侧时,
则,
解得:;
综上:n的取值范围为或.
16.
设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,
依题意,得:,
解得,
答:甲种奖品的单价为20元/件,乙种奖品的单价为10元/件.
(2)
设购买甲种奖品m件,则购买乙种奖品(60-m)件,设购买两种奖品的总费用为w元,
∵甲种奖品的数量不少于乙种奖品数量的一半,
∴m≥(60-m),
∴m≥20.
依题意,得:w=20m+10(60-m)=10m+600,
∵10>0,
∴w随m值的增大而增大,
∴当学校购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.
17.
设今年每套A型一体机的价格为x万元,每套B型一体机的价格为y万元,
由题意得:,
解得:
答:今年每套A型一体机的价格为1.2万元,每套B型一体机的价格为1.8万元;
(2)
设该市明年购买A型一体机m套,则购买B型一体机(1100-m)套,
由题意可得:1.8(1100-m)≥1.2(1+25%)m,
解得:m≤600,
设明年需投入W万元,
W=1.2×(1+25%)m+1.8(1100-m)
=-0.3m+1980,
∵-0.3<0,
∴W随m的增大而减小,
∵m≤600,
∴当m=600时,W有最小值-0.3×600+1980=1800,
故该市明年至少需投入1800万元才能完成采购计划.
18.
解:由图象可得b=15÷1×2=30米,
故答案为:30.
(2)
解:设甲距地面的高度与登山时间的关系式y=kx+m,
由图象可得,过点C(0,100)、D(20,300),
∴,解得,
∴甲距地面的高度与登山时间的关系式y=10x+100;
一次项的系数是表示甲登山的速度;
(3)
解:甲登山速度为(300-100)÷20=10(米/分钟),
当0≤x≤2时,y=15x;当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0 x 20),
当10x+100 (30x 30)=70时,解得:x=3;
当30x 30 (10x+100)=70时,解得:x=10;
当300 (10x+100)=70时,解得:x=13.
∴登山3分钟、10分钟或13分钟时,甲乙两人距离地面的高度差为70米.
19.
(1)
根据图象,得
甲、乙两地之间的距为900km.
故答案为:900;
(2)
由函数图象,当慢车行驶4h时,慢车和快车相遇.
故答案为:4;
(3)
由题意,得
快车与慢车的速度和为:900÷4=225(km/h),
慢车的速度为:900÷12=75(km/h),
快车的速度为:225﹣75=150 (km/h).
答:快车的速度为150km/h,慢车的速度为75km/h;
(4)
由题意,得快车走完全程的时间按为:900÷150=6(h),
6h时两车之间的距离为:225×(6﹣4)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
,
解得:,
则y=225x﹣900,自变量x的取值范围是4≤x≤6.
20.
解:设y乙与x的函数关系式是,
∵点E(0,12),F(2,0)在函数y乙=kx+b的图象上,
∴ ,解得 ,
即y乙与x的函数关系式是,
当x=0.5时,,
即两人相遇地点P与A地的距离是9km;
(2)
解:设线段OC对应的y甲与x的函数关系式是y甲=ax,
∵点(0.5,9)在函数y甲=ax的图象上,
∴9=0.5a, 解得a=18,
即线段OP对应的y甲与x的函数关系式是y甲=18x;
(3)
解:①令 即
或
解得:或
甲从A地到达B地的时间为:小时,
经检验:不符合题意,舍去,
②当甲到达B地时,乙离B地6千米所走时间为:
(小时),
综上所述,经过小时或1小时,甲、乙两人相距6km.
答案第1页,共2页
