数学人教A版(2019)选择性必修第二册5.3函数的最大(小)值(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.3函数的最大(小)值(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 19:16:36 | ||
图片预览







文档简介
(共20张PPT)
第五章 一元函数的导数及其应
5.2.3函数的最大(小)值
学习目标
1.能利用导数求某些函数的在给定闭区间上不超过三次的多项式函数的最大值、最小值.
2.体会导数与单调性、极值、最大(小)值的关系.
温故知新
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
1.最大值:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值
2.最小值:
(1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
3.求函数最值的一般方法
一是利用函数性质 二是利用不等式
三是利用导数
新知探究
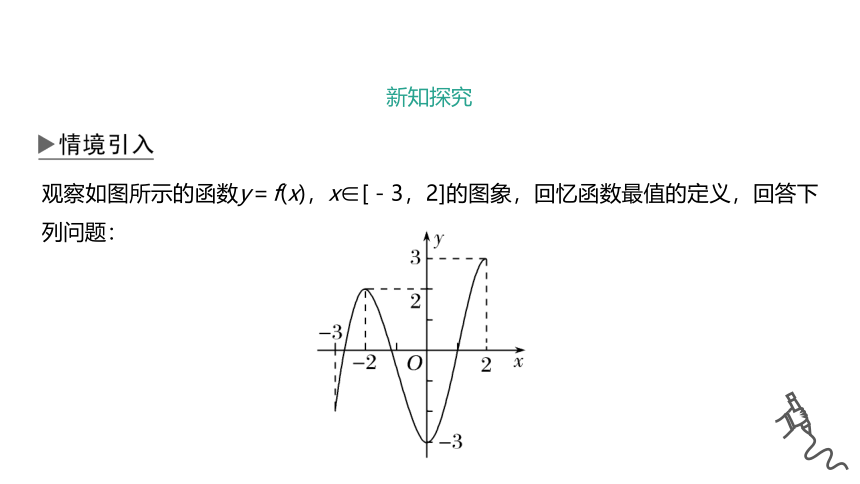
观察如图所示的函数y=f(x),x∈[-3,2]的图象,回忆函数最值的定义,回答下列问题:
问题1 图中所示函数最值点与最值分别是什么?
提示 最大值点是x=2,最大值是3;
最小值点是x=0,最小值是-3.
问题2 图中所示函数的极值点与极值分别是什么?
提示 极大值点是x=-2,极大值是2;
极小值点是x=0,极小值是-3.
问题3 一般地,函数的最值与函数的极值有什么关系?
提示 函数的最值可能是极值,也可能是区间端点的函数值.
探索新知
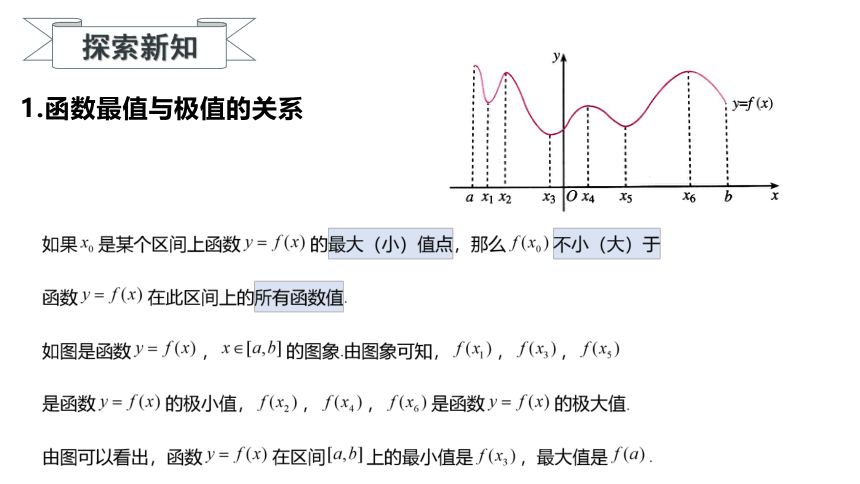
1.函数最值与极值的关系
1.
(1)函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,则该函数在[a,b]上一定能够取得最大值与最小值,函数的最值必在_____处或_______处取得.
(2)求函数y=f(x)在[a,b]上最值的步骤
①求函数y=f(x)在(a,b)内的______.
②将函数y=f(x)的各极值与________的函数值f(a),f(b)比较,其中最大的一个是________,最小的一个是________.
端点
极值点
极值
端点处
最大值
函数的最大值与最小值最多只有一个,极大值与极小值则可能有多个
函数f(x)在闭区间[a,b]上的最值
最小值
2.最值与极值的区别与联系
(1)极值是对某一点附近(即局部)而言,最值是对函数的定义区间的整体而言.
(2)在函数的定义区间内,极大(小)值可能有多个,但最大(小)值只有一个(或者没有).
(3)函数f(x)的极值点为定义域中的内点,而最值点可以是区间的端点.
(4)对于可导函数,函数的最大(小)值必在极大(小)值点或区间端点处取得.
题型一 求函数的最值
【例1】 求下列各函数的最值.
解 (1)f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,
∵f′(x)在[-1,1]内恒大于0,∴f(x)在[-1,1]上为增函数.
故当x=-1时,f(x)min=-12;
当x=1时,f(x)max=2.
即f(x)的最小值为-12,最大值为2.
解:
令
解得
x
0
(0, )
( , )
+
-
+
0
0
( , )
当x变化时, ,f(x)的变化情况如下表:
0
求函数y=f (x)在[a,b]上的最大值与最小值的步骤:
①求函数y=f (x)在(a,b)内的极值;
②将函数y=f (x)的各极值与端点处的函数值f (a), f (b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意
1) 函数的最值概念是全局性的
2) 函数的最大值(最小值)唯一
3) 函数的最大值大于等于最小值
4) 函数的最值可在端点处取得
题型二 含参数的函数的最值问题
【例2】 已知f(x)=ax-ln x,a∈R.
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;(2)是否存在实数a,使f(x)在区间(0,e]上的最小值是3,若存在,求出a的值;若不存在,说明理由.
①当a≤0时,f(x)在(0,e]上单调递减,
综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.
题型三 由函数的最值求参数问题
【例3】 已知函数f(x)=ax3-6ax2+b,x∈[-1,2]时,f(x)的最大值为3,最小值为-29,求a,b的值.
解 由题设知a≠0,否则f(x)=b为常数,与题设矛盾.
∵f′(x)=3ax2-12ax=3ax(x-4),
令f′(x)=0,得x1=0,x2=4(舍去).
(1)当a>0时,列表如下:
x -1 (-1,0) 0 (0,2) 2
f′(x) + 0 -
f(x) -7a+b ? b ? -16a+b
由表可知,当x=0时,f(x)取得最大值.
∴f(0)=3,即b=3.
又f(-1)=-7a+3,f(2)=-16a+3∴f(2)=-16a+3=-29,∴a=2.
(2)当a<0时,同理可得,当x=0时,f(x)取得最小值f(0)=-29,∴b=-29.
又f(-1)=-7a-29,f(2)=-16a-29>f(-1),
∴f(2)=-16a-29=3,∴a=-2.
综上可得,a=2,b=3或a=-2,b=-29.
1.通过学习函数最值的概念及求解方法,培养数学抽象和数学运算素养.
2.求函数在闭区间上的最值,只需比较极值和端点处的函数值即可;若函数在一个开区间内只有一个极值,这个极值就是最值.
3.已知最值求参数时,可先用参数表示最值,有时需分类讨论.
谢谢大家!
第五章 一元函数的导数及其应
5.2.3函数的最大(小)值
学习目标
1.能利用导数求某些函数的在给定闭区间上不超过三次的多项式函数的最大值、最小值.
2.体会导数与单调性、极值、最大(小)值的关系.
温故知新
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
1.最大值:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值
2.最小值:
(1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
3.求函数最值的一般方法
一是利用函数性质 二是利用不等式
三是利用导数
新知探究
观察如图所示的函数y=f(x),x∈[-3,2]的图象,回忆函数最值的定义,回答下列问题:
问题1 图中所示函数最值点与最值分别是什么?
提示 最大值点是x=2,最大值是3;
最小值点是x=0,最小值是-3.
问题2 图中所示函数的极值点与极值分别是什么?
提示 极大值点是x=-2,极大值是2;
极小值点是x=0,极小值是-3.
问题3 一般地,函数的最值与函数的极值有什么关系?
提示 函数的最值可能是极值,也可能是区间端点的函数值.
探索新知
1.函数最值与极值的关系
1.
(1)函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,则该函数在[a,b]上一定能够取得最大值与最小值,函数的最值必在_____处或_______处取得.
(2)求函数y=f(x)在[a,b]上最值的步骤
①求函数y=f(x)在(a,b)内的______.
②将函数y=f(x)的各极值与________的函数值f(a),f(b)比较,其中最大的一个是________,最小的一个是________.
端点
极值点
极值
端点处
最大值
函数的最大值与最小值最多只有一个,极大值与极小值则可能有多个
函数f(x)在闭区间[a,b]上的最值
最小值
2.最值与极值的区别与联系
(1)极值是对某一点附近(即局部)而言,最值是对函数的定义区间的整体而言.
(2)在函数的定义区间内,极大(小)值可能有多个,但最大(小)值只有一个(或者没有).
(3)函数f(x)的极值点为定义域中的内点,而最值点可以是区间的端点.
(4)对于可导函数,函数的最大(小)值必在极大(小)值点或区间端点处取得.
题型一 求函数的最值
【例1】 求下列各函数的最值.
解 (1)f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,
∵f′(x)在[-1,1]内恒大于0,∴f(x)在[-1,1]上为增函数.
故当x=-1时,f(x)min=-12;
当x=1时,f(x)max=2.
即f(x)的最小值为-12,最大值为2.
解:
令
解得
x
0
(0, )
( , )
+
-
+
0
0
( , )
当x变化时, ,f(x)的变化情况如下表:
0
求函数y=f (x)在[a,b]上的最大值与最小值的步骤:
①求函数y=f (x)在(a,b)内的极值;
②将函数y=f (x)的各极值与端点处的函数值f (a), f (b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意
1) 函数的最值概念是全局性的
2) 函数的最大值(最小值)唯一
3) 函数的最大值大于等于最小值
4) 函数的最值可在端点处取得
题型二 含参数的函数的最值问题
【例2】 已知f(x)=ax-ln x,a∈R.
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;(2)是否存在实数a,使f(x)在区间(0,e]上的最小值是3,若存在,求出a的值;若不存在,说明理由.
①当a≤0时,f(x)在(0,e]上单调递减,
综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.
题型三 由函数的最值求参数问题
【例3】 已知函数f(x)=ax3-6ax2+b,x∈[-1,2]时,f(x)的最大值为3,最小值为-29,求a,b的值.
解 由题设知a≠0,否则f(x)=b为常数,与题设矛盾.
∵f′(x)=3ax2-12ax=3ax(x-4),
令f′(x)=0,得x1=0,x2=4(舍去).
(1)当a>0时,列表如下:
x -1 (-1,0) 0 (0,2) 2
f′(x) + 0 -
f(x) -7a+b ? b ? -16a+b
由表可知,当x=0时,f(x)取得最大值.
∴f(0)=3,即b=3.
又f(-1)=-7a+3,f(2)=-16a+3
(2)当a<0时,同理可得,当x=0时,f(x)取得最小值f(0)=-29,∴b=-29.
又f(-1)=-7a-29,f(2)=-16a-29>f(-1),
∴f(2)=-16a-29=3,∴a=-2.
综上可得,a=2,b=3或a=-2,b=-29.
1.通过学习函数最值的概念及求解方法,培养数学抽象和数学运算素养.
2.求函数在闭区间上的最值,只需比较极值和端点处的函数值即可;若函数在一个开区间内只有一个极值,这个极值就是最值.
3.已知最值求参数时,可先用参数表示最值,有时需分类讨论.
谢谢大家!
