苏科版七年级数学下册 8.3 同底数幂的除法 课件(共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 8.3 同底数幂的除法 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 08:36:47 | ||
图片预览





文档简介
(共19张PPT)
8.3 同底数幂的除法
2.am÷an= (a≠0, m、n都是正 整数,且m>n)
1.同底数幂相除,底数____, 指数____.
不变
相减
am–n
自主预习
3.计算:
(1) 279÷97÷3
(2) b2m÷bm-1(m是大于1的整数)
(3) (-mn)9÷(mn)4
(4) (a-b)6÷(b-a)3÷(a-b)2
目标展示
1.掌握零指数幂与负指数幂。
2.会正确地运用。
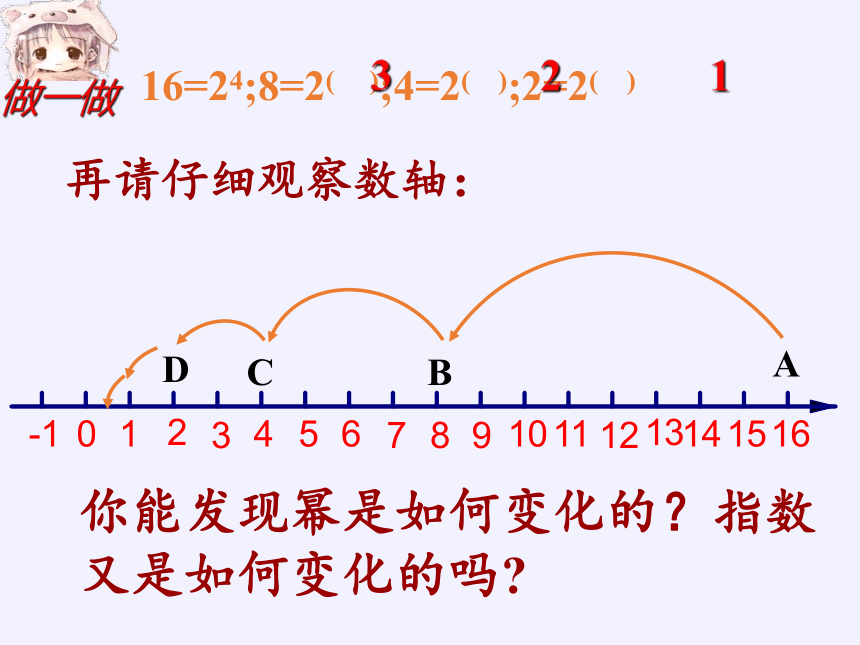
16=24;8=2( );4=2( );2=2( )
做一做
3
2
1
你能发现幂是如何变化的?指数又是如何变化的吗
A
B
C
D
再请仔细观察数轴:
3
2
1
0
–1
–2
–3
会填吗?
猜一猜
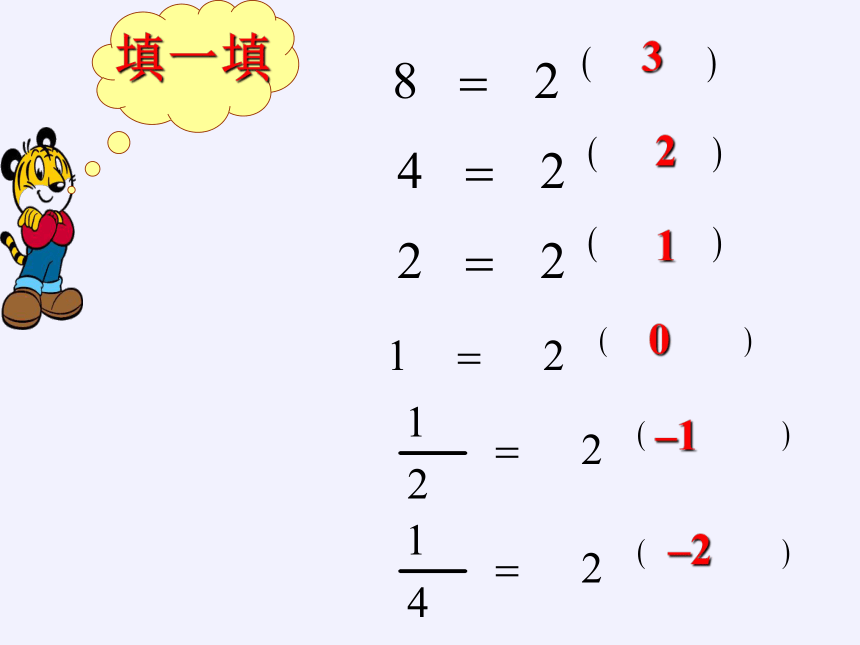
3
2
1
0
–1
–2
填一填
猜想:你能得到何结论
a0 — 零指数幂;
a–p — 负指数幂。
0
–1
–2
–3
1
a
0
=
)
0
a
(
a
1
a
n
n
=
-
(
)
,
0
a
n是正 整数
你能说明理由吗?
结论:
∴ 规定 a0 =1;
am–m
am÷am=
=
a0,
1=
当n是正整数时,
=a0÷a n
=a0–n
=a–n
∴ 规定 :
你能用文字语言叙述这个性质吗?
①任何不等于0的数的0次幂等于1.
② 任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
20=____. 22=___,
2-2=____, (-2)2=___,
(-2)-2=____, 10-3=____,
(-10)-3=____, (-10)0=___.
1
4
4
1
个性展示
个0
n
个0
n
(n为正整数)
请细心观察
结论:
例题解析
例:用小数或分数表示下列各数
(1) ;(2) ;(3)
解:
(1)
(2)
(3)
填空
(2) , 则x=___.
(3)256b=25×211,则b=__.
(5)若0.0000003=3×10m,则 m=___.
-5
2
-2
-7
(1)107=________ ,10-5=________.
10000000
0.00001
22-2-2+(-2)-2
5-16×(-2)3
(3)4-(-2)-2-32÷(-3)0
10-2×100+103÷105
计算
整合提升
我要说…
2.我从同伴身上学到了什么
1.这节课我学到了什么?
小结
1.计算:
(1) 279÷97÷3
(2) b2m÷bm-1(m是大于1的整数)
(3) (-mn)9÷(mn)4
(4) (a-b)6÷(b-a)3÷(a-b)2
2.已知am=3,an=2,求a2m-3n的值.
布置作业
见学案
谢 谢
8.3 同底数幂的除法
2.am÷an= (a≠0, m、n都是正 整数,且m>n)
1.同底数幂相除,底数____, 指数____.
不变
相减
am–n
自主预习
3.计算:
(1) 279÷97÷3
(2) b2m÷bm-1(m是大于1的整数)
(3) (-mn)9÷(mn)4
(4) (a-b)6÷(b-a)3÷(a-b)2
目标展示
1.掌握零指数幂与负指数幂。
2.会正确地运用。
16=24;8=2( );4=2( );2=2( )
做一做
3
2
1
你能发现幂是如何变化的?指数又是如何变化的吗
A
B
C
D
再请仔细观察数轴:
3
2
1
0
–1
–2
–3
会填吗?
猜一猜
3
2
1
0
–1
–2
填一填
猜想:你能得到何结论
a0 — 零指数幂;
a–p — 负指数幂。
0
–1
–2
–3
1
a
0
=
)
0
a
(
a
1
a
n
n
=
-
(
)
,
0
a
n是正 整数
你能说明理由吗?
结论:
∴ 规定 a0 =1;
am–m
am÷am=
=
a0,
1=
当n是正整数时,
=a0÷a n
=a0–n
=a–n
∴ 规定 :
你能用文字语言叙述这个性质吗?
①任何不等于0的数的0次幂等于1.
② 任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
20=____. 22=___,
2-2=____, (-2)2=___,
(-2)-2=____, 10-3=____,
(-10)-3=____, (-10)0=___.
1
4
4
1
个性展示
个0
n
个0
n
(n为正整数)
请细心观察
结论:
例题解析
例:用小数或分数表示下列各数
(1) ;(2) ;(3)
解:
(1)
(2)
(3)
填空
(2) , 则x=___.
(3)256b=25×211,则b=__.
(5)若0.0000003=3×10m,则 m=___.
-5
2
-2
-7
(1)107=________ ,10-5=________.
10000000
0.00001
22-2-2+(-2)-2
5-16×(-2)3
(3)4-(-2)-2-32÷(-3)0
10-2×100+103÷105
计算
整合提升
我要说…
2.我从同伴身上学到了什么
1.这节课我学到了什么?
小结
1.计算:
(1) 279÷97÷3
(2) b2m÷bm-1(m是大于1的整数)
(3) (-mn)9÷(mn)4
(4) (a-b)6÷(b-a)3÷(a-b)2
2.已知am=3,an=2,求a2m-3n的值.
布置作业
见学案
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
