教科版物理八年级下册 11.1 杠杆(共21张PPT)
文档属性
| 名称 | 教科版物理八年级下册 11.1 杠杆(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
1. 杠杆
生活中常见的杠杆
一、杠杆
在日常生活中,你见过、使用过下面这些工具吗?想想你是在什么情况下或看见别人怎样使用的,在使用这些工具时,有哪些相同的地方?把你的看法说出来或写下来,和大家一起交流。
1.撬棒
2.跷跷板
3.抽水机的柄
思考:它们在使用时有什
么共同点?
认识杠杆
有力的作用
绕固定点转动
硬棒
在力的作用下,能绕某一固定点转动的硬棒.
1、杠杆:
认识杠杆
作为杠杆的物体可以是直的,也可以是弯的,但必须是硬的、坚实的,不易发生形变的。你还能举出生活中其他杠杆的事例吗
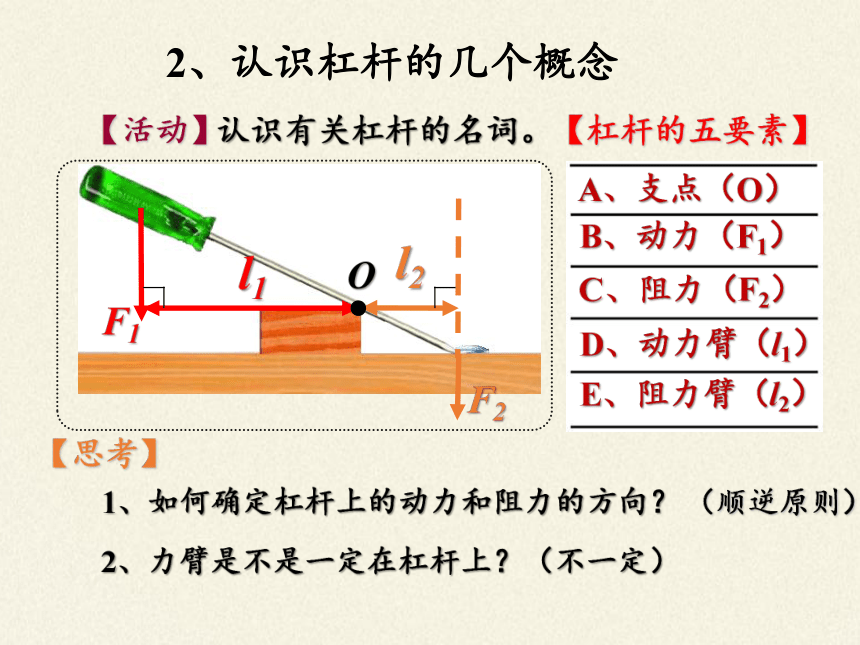
2、认识杠杆的几个概念
【思考】
认识有关杠杆的名词。
【活动】
A、支点(O)
B、动力(F1)
C、阻力(F2)
D、动力臂(l1)
E、阻力臂(l2)
【杠杆的五要素】
1、如何确定杠杆上的动力和阻力的方向?
2、力臂是不是一定在杠杆上?(不一定)
(顺逆原则)
l1
l2
O
F1
F2
F1
l2
l1
F2
o
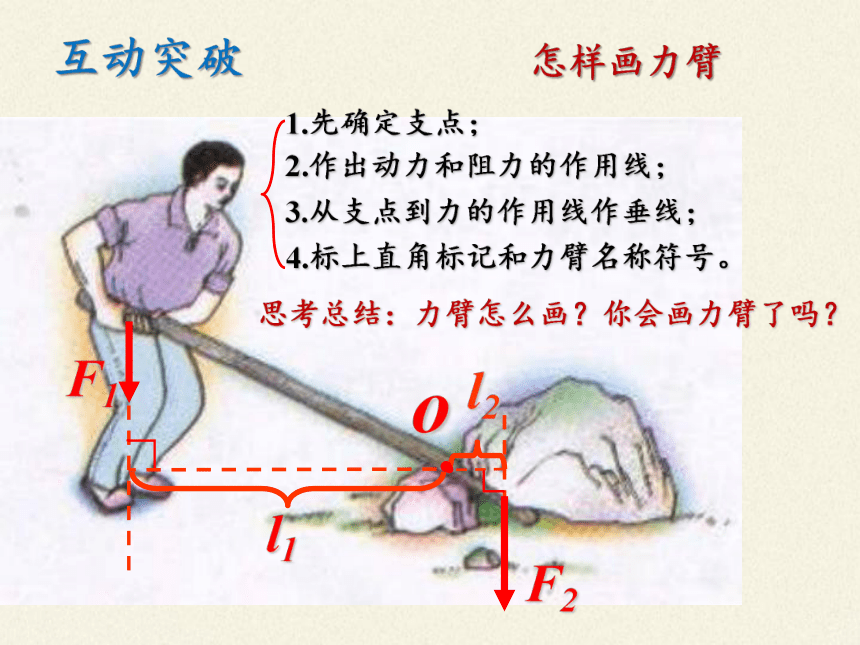
互动突破 怎样画力臂
1.先确定支点;
2.作出动力和阻力的作用线;
3.从支点到力的作用线作垂线;
4.标上直角标记和力臂名称符号。
思考总结:力臂怎么画?你会画力臂了吗?
例1 如图所示的杠杆中,O是 ,若设F1是动力,则F2是 ,动力臂是 ,阻力臂是 。
例2 在下图杠杆中,画出对应的力或力臂。
例题解析
支点
阻力
OA
OB
F1
l1
二 杠杆的平衡
归纳结论:
1.当杠杆在动力和阻力的作用下静止时,或缓慢地匀速转动,我们说杠杆平衡了。
用杆秤称量物体的质量时,什么时候我们认为杆秤平衡了?
探究杠杆的平衡条件
提问:什么是杠杆的平衡?
归纳:
杠杆处于静止或匀速转动,我们就说杠杆平衡了
提问:杠杆平衡时,其动力、动力臂、阻力、阻力臂之间存在怎样的关系?
猜想与假设:
杠杆平衡的条件:动力×动力臂=阻力×阻力臂
探究杠杆的平衡条件
设计实验:
实验器材: .
测量的物理量: .
观察下面A、B两幅图,思考:
1.杠杆两端装置两只可调节的螺母,能起什么作用?
答:调节杠杆在水平位置平衡.
2. 两图中杠杆均保持静止,哪个图中杠杆是平衡的?实验时采用哪幅图?为什么?
答:实验前可以避免杠杆自重对平衡的影响,实验时便于测量力臂.
杠杆、钩码、支架、弹簧测力计等
动力、动力臂、阻力、阻力臂
(1)调节杠杆两端的螺母,使杠杆在水平位置平衡;
进行实验
4、
(2)在杠杆两边挂上钩码,调节钩码的位置,使杠杆在水平位置重新平衡,记录F1,L1,F2,L2;
实验步骤:
(3)改变钩码数量或位置,重复上面的步骤,得出三组数据。
杠杆的平衡条件是:
5.得出结论
动力×动力臂=阻力×阻力臂
F1 · L1=F2 · L2
杠杆两端可调节的平衡螺母,起什么作用
为什么要求杠杆静止时,在水平位置
平衡螺母调节杠杆自身的平衡。
力臂的数值在杠杆上可以直接读出或量出。
评估 与 交流
挂钩码后,能不能再调节平衡螺母?
不能。
该实验还有什么注意事项?
该实验为什么要进行多次?
F2
F1
9.如图用弹簧秤斜向上拉杠杆,力有什么变化?
1.练习
l1=3l2,F1是F2的___倍。
F1:F2=2:5,l1:l2=____。
l1:l2=4:3,F2=60 N,F1=___。
F1=15 N,F2=75 N,l1=15 cm,l2=___。
3、杠杆的平衡条件应用
O
l1=9m
l2=6cm
F1=200N
F2
杠杆的平衡条件应用
例题:
由F1l1=F2l2 得:
解:
F2
=
F1 l1
l2
=
200N×9m
0.06m
=3×104N
m
=
F2
g
=
10N·kg—1
3×104N
=3×103kg = 3 t
1、学习了杠杆、支点、动力、
阻力、动力臂、阻力臂等概念.
2、探究了杠杆的平衡条件是
F1 · L1=F2 · L2
小结:
谢 谢
1. 杠杆
生活中常见的杠杆
一、杠杆
在日常生活中,你见过、使用过下面这些工具吗?想想你是在什么情况下或看见别人怎样使用的,在使用这些工具时,有哪些相同的地方?把你的看法说出来或写下来,和大家一起交流。
1.撬棒
2.跷跷板
3.抽水机的柄
思考:它们在使用时有什
么共同点?
认识杠杆
有力的作用
绕固定点转动
硬棒
在力的作用下,能绕某一固定点转动的硬棒.
1、杠杆:
认识杠杆
作为杠杆的物体可以是直的,也可以是弯的,但必须是硬的、坚实的,不易发生形变的。你还能举出生活中其他杠杆的事例吗
2、认识杠杆的几个概念
【思考】
认识有关杠杆的名词。
【活动】
A、支点(O)
B、动力(F1)
C、阻力(F2)
D、动力臂(l1)
E、阻力臂(l2)
【杠杆的五要素】
1、如何确定杠杆上的动力和阻力的方向?
2、力臂是不是一定在杠杆上?(不一定)
(顺逆原则)
l1
l2
O
F1
F2
F1
l2
l1
F2
o
互动突破 怎样画力臂
1.先确定支点;
2.作出动力和阻力的作用线;
3.从支点到力的作用线作垂线;
4.标上直角标记和力臂名称符号。
思考总结:力臂怎么画?你会画力臂了吗?
例1 如图所示的杠杆中,O是 ,若设F1是动力,则F2是 ,动力臂是 ,阻力臂是 。
例2 在下图杠杆中,画出对应的力或力臂。
例题解析
支点
阻力
OA
OB
F1
l1
二 杠杆的平衡
归纳结论:
1.当杠杆在动力和阻力的作用下静止时,或缓慢地匀速转动,我们说杠杆平衡了。
用杆秤称量物体的质量时,什么时候我们认为杆秤平衡了?
探究杠杆的平衡条件
提问:什么是杠杆的平衡?
归纳:
杠杆处于静止或匀速转动,我们就说杠杆平衡了
提问:杠杆平衡时,其动力、动力臂、阻力、阻力臂之间存在怎样的关系?
猜想与假设:
杠杆平衡的条件:动力×动力臂=阻力×阻力臂
探究杠杆的平衡条件
设计实验:
实验器材: .
测量的物理量: .
观察下面A、B两幅图,思考:
1.杠杆两端装置两只可调节的螺母,能起什么作用?
答:调节杠杆在水平位置平衡.
2. 两图中杠杆均保持静止,哪个图中杠杆是平衡的?实验时采用哪幅图?为什么?
答:实验前可以避免杠杆自重对平衡的影响,实验时便于测量力臂.
杠杆、钩码、支架、弹簧测力计等
动力、动力臂、阻力、阻力臂
(1)调节杠杆两端的螺母,使杠杆在水平位置平衡;
进行实验
4、
(2)在杠杆两边挂上钩码,调节钩码的位置,使杠杆在水平位置重新平衡,记录F1,L1,F2,L2;
实验步骤:
(3)改变钩码数量或位置,重复上面的步骤,得出三组数据。
杠杆的平衡条件是:
5.得出结论
动力×动力臂=阻力×阻力臂
F1 · L1=F2 · L2
杠杆两端可调节的平衡螺母,起什么作用
为什么要求杠杆静止时,在水平位置
平衡螺母调节杠杆自身的平衡。
力臂的数值在杠杆上可以直接读出或量出。
评估 与 交流
挂钩码后,能不能再调节平衡螺母?
不能。
该实验还有什么注意事项?
该实验为什么要进行多次?
F2
F1
9.如图用弹簧秤斜向上拉杠杆,力有什么变化?
1.练习
l1=3l2,F1是F2的___倍。
F1:F2=2:5,l1:l2=____。
l1:l2=4:3,F2=60 N,F1=___。
F1=15 N,F2=75 N,l1=15 cm,l2=___。
3、杠杆的平衡条件应用
O
l1=9m
l2=6cm
F1=200N
F2
杠杆的平衡条件应用
例题:
由F1l1=F2l2 得:
解:
F2
=
F1 l1
l2
=
200N×9m
0.06m
=3×104N
m
=
F2
g
=
10N·kg—1
3×104N
=3×103kg = 3 t
1、学习了杠杆、支点、动力、
阻力、动力臂、阻力臂等概念.
2、探究了杠杆的平衡条件是
F1 · L1=F2 · L2
小结:
谢 谢
