苏科版七年级数学下册 12.2 证明 课件(共20张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 12.2 证明 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 874.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 09:22:29 | ||
图片预览








文档简介
(共20张PPT)
12.2 证明
试一试
利用手中的工具,将三角形的
三个角拼成180°.
同桌两人合作完成:
比哪一组想的方法多!
12.2 证明(3)
三角形内角和
学习目标
1.能通过添加辅助线的方法证明
三角形内角和定理 .
2.掌握三角形内角和定理和它的
推论.
自学指导一
认真看课本P.153“议一议”
前面的内容:
1.思考:课本中添加的辅助线有何作用?
2.参照黑板上的拼图想一想:你还有其
它添加辅助线的方法吗?(在作业纸上
画出来.)
3分钟后,比谁能模仿课本写出其它
方法的证明过程.
证明:三角形三个内角的
和等于180 0 .
参照黑板上的拼图完成证明.
开启 智慧
为了证明的需要,在原来图形
上添画的线叫辅助线.
注意:辅助线通常画成虚线.
知识归纳
A
(1)
B
C
P
Q
R
T
S
N
(2)
A
B
C
P
Q
R
M
T
S
N
A
B
C
P
Q
R
M
(3)
(
(
(
2
3
A
B
C
E
D
F
1
4
(
(4)
A
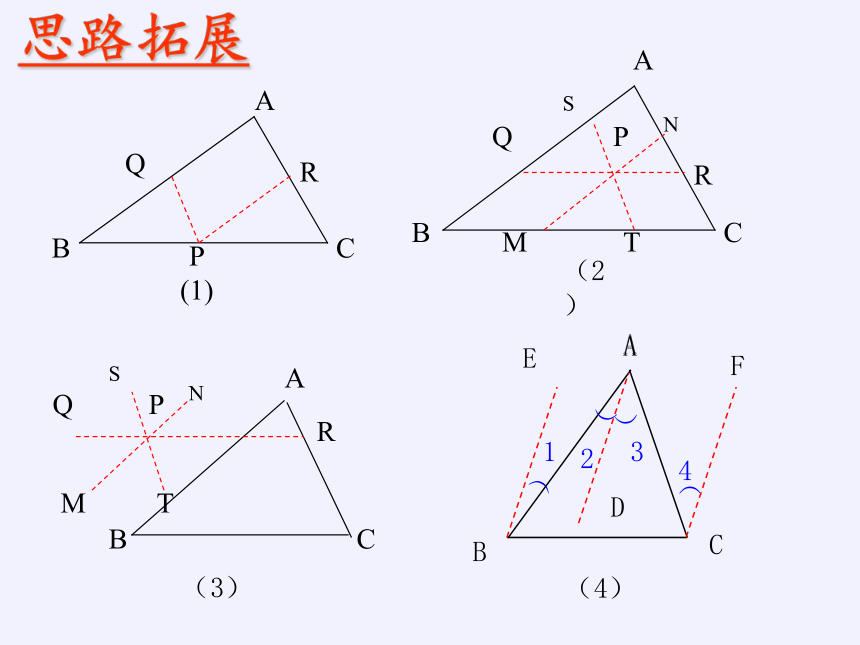
思路拓展
在△ABC中,
∠A+∠B+∠C=1800
(三角形三个内角的和等于1800).
在△ABC中,
∠A+∠B+∠C=1800
(三角形三个内角的和等于1800).
用量角器测量下列各角的度数:
∠A= ____
∠B= ____
∠ACD= ____
∠A= ____
∠B= ____
∠ACD= ____
思考∠A+∠B与∠ACD之间的数量关系.
∠A+∠B=∠ACD
探索归纳
∠A= ____
∠B= ____
∠ACD= ____
450
300
750
600
300
900
450
600
1050
(1)
(2)
(3)
证明:在△ ABC中,∠A+∠B+∠ACB=180°
(三角形三个内角的和等于180°).
∴ ∠A+∠B=180°-∠ACB(等式性质).
∵∠ACD+∠ACB=180°(平角的定义),
∴∠ACD=180°-∠ACB(等式性质).
∴∠ACD= ∠A+∠B(等量代换).
三角形的外角等于与它不相邻的
两个内角的和.
已知:
求证:
∠ACD是△ABC的外角.
∠ACD = ∠A+∠B.
A
C
B
D
三角形内角和定理的推论:
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B
(三角形的外角等于与它不相邻的两个
内角的和).
用>、<、= 填空:
∠ACD ____ ∠A;
∠ACD ____ ∠B;
>
>
自学指导二
认真看课本P.154的例2,
要求:
1.思考每一步证明的依据;
2.尝试用三角形内角和定理的推
论证明例2.
3分钟后,比谁能做对相应的练习.
1.已知:如图,AC﹑BD相交于点O.
求证:∠A+∠B=∠C+∠D.
尝试用三角形内角和定理的推论证明.
实战演习
2.已知:如图,AD是△ABC的角平分线,
E是BC延长线上一点,∠EAC=∠B.
求证:∠ADE = ∠DAE.
第 1 题
第 2 题
如图:
∠A+ ∠B+ ∠E+ ∠F+ ∠G+ ∠H=_____ .
360o
拓展延伸:
知识树
三角形的内角和定理
推论
转化角的方法
转化思想
不同的证明方法
辅助线的作法、作用
应用
……
……
……
……
……
……
……
课堂感悟
课堂作业
必做题:课本 (1) P.156 T8
选做题:如图:∠A+∠B+∠C+∠D+∠E= .
思考题:如图:AC、BD相交于点O,∠CAD与∠CBD
的平分线相交于点P.求证:2∠P=∠C+∠D.
作业要求:
1.书写工整.2.解题完整、规范.
思考题图
选做题图
谢谢,请多提宝贵意见!
谢 谢
12.2 证明
试一试
利用手中的工具,将三角形的
三个角拼成180°.
同桌两人合作完成:
比哪一组想的方法多!
12.2 证明(3)
三角形内角和
学习目标
1.能通过添加辅助线的方法证明
三角形内角和定理 .
2.掌握三角形内角和定理和它的
推论.
自学指导一
认真看课本P.153“议一议”
前面的内容:
1.思考:课本中添加的辅助线有何作用?
2.参照黑板上的拼图想一想:你还有其
它添加辅助线的方法吗?(在作业纸上
画出来.)
3分钟后,比谁能模仿课本写出其它
方法的证明过程.
证明:三角形三个内角的
和等于180 0 .
参照黑板上的拼图完成证明.
开启 智慧
为了证明的需要,在原来图形
上添画的线叫辅助线.
注意:辅助线通常画成虚线.
知识归纳
A
(1)
B
C
P
Q
R
T
S
N
(2)
A
B
C
P
Q
R
M
T
S
N
A
B
C
P
Q
R
M
(3)
(
(
(
2
3
A
B
C
E
D
F
1
4
(
(4)
A
思路拓展
在△ABC中,
∠A+∠B+∠C=1800
(三角形三个内角的和等于1800).
在△ABC中,
∠A+∠B+∠C=1800
(三角形三个内角的和等于1800).
用量角器测量下列各角的度数:
∠A= ____
∠B= ____
∠ACD= ____
∠A= ____
∠B= ____
∠ACD= ____
思考∠A+∠B与∠ACD之间的数量关系.
∠A+∠B=∠ACD
探索归纳
∠A= ____
∠B= ____
∠ACD= ____
450
300
750
600
300
900
450
600
1050
(1)
(2)
(3)
证明:在△ ABC中,∠A+∠B+∠ACB=180°
(三角形三个内角的和等于180°).
∴ ∠A+∠B=180°-∠ACB(等式性质).
∵∠ACD+∠ACB=180°(平角的定义),
∴∠ACD=180°-∠ACB(等式性质).
∴∠ACD= ∠A+∠B(等量代换).
三角形的外角等于与它不相邻的
两个内角的和.
已知:
求证:
∠ACD是△ABC的外角.
∠ACD = ∠A+∠B.
A
C
B
D
三角形内角和定理的推论:
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B
(三角形的外角等于与它不相邻的两个
内角的和).
用>、<、= 填空:
∠ACD ____ ∠A;
∠ACD ____ ∠B;
>
>
自学指导二
认真看课本P.154的例2,
要求:
1.思考每一步证明的依据;
2.尝试用三角形内角和定理的推
论证明例2.
3分钟后,比谁能做对相应的练习.
1.已知:如图,AC﹑BD相交于点O.
求证:∠A+∠B=∠C+∠D.
尝试用三角形内角和定理的推论证明.
实战演习
2.已知:如图,AD是△ABC的角平分线,
E是BC延长线上一点,∠EAC=∠B.
求证:∠ADE = ∠DAE.
第 1 题
第 2 题
如图:
∠A+ ∠B+ ∠E+ ∠F+ ∠G+ ∠H=_____ .
360o
拓展延伸:
知识树
三角形的内角和定理
推论
转化角的方法
转化思想
不同的证明方法
辅助线的作法、作用
应用
……
……
……
……
……
……
……
课堂感悟
课堂作业
必做题:课本 (1) P.156 T8
选做题:如图:∠A+∠B+∠C+∠D+∠E= .
思考题:如图:AC、BD相交于点O,∠CAD与∠CBD
的平分线相交于点P.求证:2∠P=∠C+∠D.
作业要求:
1.书写工整.2.解题完整、规范.
思考题图
选做题图
谢谢,请多提宝贵意见!
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
