沪科版九年级下册数学阶段达标检测卷—第24章 圆(24.1~24.3)(含答案)
文档属性
| 名称 | 沪科版九年级下册数学阶段达标检测卷—第24章 圆(24.1~24.3)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆(24.1~24.3)】
本试卷共8大题,计23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A B C D
2.若正方形ABCD的四个顶点都在☉O上,则边AB所对的圆心角的度数是( )
A.45° B.90° C.120° D.135°
3.用反证法证明“是无理数”时,第一个步骤是先假设( )
A.是有理数 B.是整数 C.是分数 D.是实数
4.如图,若将边长为的正方形绕点B逆时针旋转30°,则图中阴影部分的面积为( )
A.3 B. C.3- D.3-
5.如图,☉A过点O(0,0),C(2,0),D(0,2),B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
6.如图,已知AB是☉O的直径,CD是☉O的弦,CD⊥AB,垂足为P.若BP∶AP=1∶5,CD=10,则☉O的半径长为( )
A.3 B.5 C.2 D.
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.已知EF=CD=16 cm,则球的半径为( )
A.10 cm B.8 cm C.10 cm D.10 cm
8.如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,将△ABC绕点A逆时针旋转得到△ADE,使得点D落在AC上,则tan ∠ECD的值为( )
A. B. C. D.
9.如图,四边形ABCD内接于☉O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin ∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
10.如图,在平面直角坐标系中,已知点P(2,4),点A(0,3),点B(4,0),C是AB的中点,将△OAB绕点O旋转一周,在旋转过程中,点P与点C距离的最小值为( )
A.-2 B.2-2.5 C.2-5 D.2.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.把点P(-6,8)绕坐标原点旋转180°后对应点的坐标为 .
12.如图,已知圆弧形桥拱的半径为10米,拱高CD=4米,那么圆弧形桥拱的跨度AB= 米.
13.如图,点A的坐标为(0,4),点B的坐标为(4,2),点C的坐标为(6,2),点D的坐标为(4,-2),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .
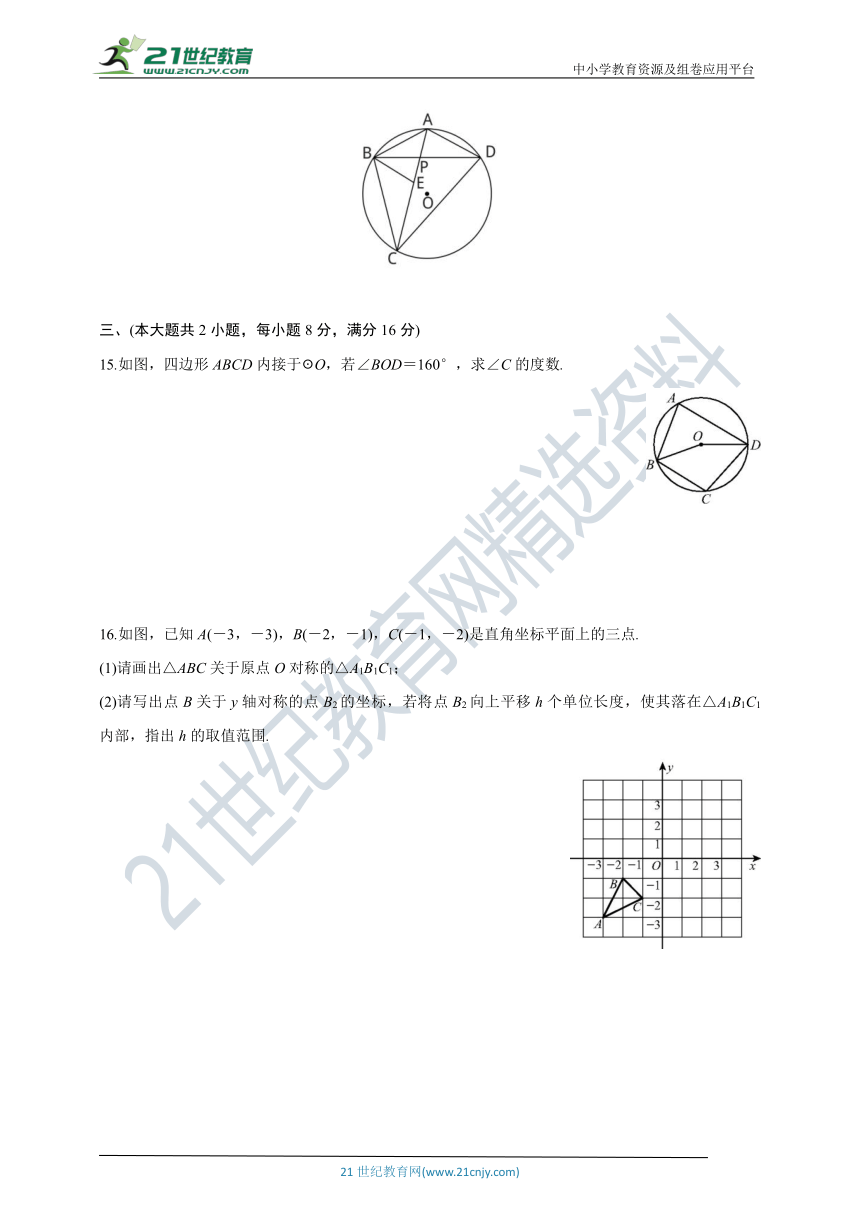
14.如图,四边形ABCD内接于☉O,对角线AC,BD交于点P,且AB=AD.若AC=7,AB=3,则
(1)AP= ;
(2)BC·CD= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,四边形ABCD内接于☉O,若∠BOD=160°,求∠C的度数.
16.如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上的三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位长度,使其落在△A1B1C1内部,指出h的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在☉O中,AB,AC为互相垂直且相等的两条弦,OD⊥AB于点D,OE⊥AC于点E.求证:四边形AEOD是正方形.
18.如图,在△AOB中,OA=OB=8,点C的坐标为(0,2),P是OB上一个动点,连接CP,将线段CP绕点C逆时针旋转90°得到线段CD,使点D恰好落在AB上.求点D的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在☉O中,C是优弧的中点,D,E分别是OA,OB上的点,且AD=BE,弦 CM,CN分别过点D,E.
(1)求证:CD=CE;
(2)求证:=.
20.如图,D是等边△ABC内一点,将线段AD绕点A逆时针旋转60°得到线段AE,连接CD并延长,交AB于点F,连接BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
六、(本题满分12分)
21.如图,△ABC是☉O的内接三角形,C是优弧上一点(点C不与点A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
七、(本题满分12分)
22.如图,有一座圆弧形拱桥,桥下水面宽度AB为12 m,拱高CD为4 m.
(1)求拱桥的半径;
(2)有一艘宽为5 m的货船,船舱顶部为长方形,且高出水面3.6 m,求此货船是否能顺利通过拱桥
八、(本题满分14分)
23.如图1,在矩形ABCD中,E是AD的中点,以E为直角顶点的直角△EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE.
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动,若EF,EG分别与AB,BC相交于点M,N(如图2).
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin ∠EBG的值.
参 考 答 案
1.D 2.B 3.A 4.C 5.B 6.A 7.D 8.B 9.C 10.B
11.(6,-8) 12.16 13.(2,0)或(5,3) 14.(1)40 (2)40
15.解:∵∠BOD=160°,∴∠A=∠BOD=80°.又∵∠A+∠C=180°,∴∠C=180°-∠A=100°.
16.解:(1)如图所示,△A1B1C1即为所求.
(2)点B2的坐标为(2,-1).观察可知,h的取值范围为217.证明:∵OD⊥AB,∴AD=BD=AB,∠ODA=90°.同理AE=CE=AC,∠OEA=90°.∵AB⊥AC,∴∠OEA=∠A=∠ODA=90°,∴四边形AEOD为矩形.又∵AB=AC,∴AD=AE,∴矩形AEOD是正方形.
18.解:过点D作DE⊥OA,垂足为E.∵线段CP绕点C逆时针旋转90°得到线段CD,∴CD=CP.∵∠PCD=90°,∴∠ECD+∠OCP=90°.又∵∠OPC+∠OCP=90°,∴∠OPC=∠ECD.在△OCP和△EDC中,∠OPC=∠ECD,∠COP=∠DEC,CD=CP,∴△OCP≌△EDC(AAS),∴DE=OC=2.∵OA=OB=8,∠AOB=90°,∴∠OAB=45°.∵DE⊥OA,∴∠DEA=90°,∴AE=DE=2,∴OE=OA-AE=8-2=6,∴点D的坐标为(2,6).
19.证明:(1)连接OC.由题意得=,∴∠COD=∠COE.∵OA=OB,AD=BE,∴OD=OE.又∵OC=OC,∴△COD≌△COE(SAS),∴CD=CE.
(2)连接OM,ON.由(1)得△COD≌△COE,∴∠ODC=∠OEC,∠OCD=∠OCE.∵OC=OM=ON,∴∠OCM=∠OMC,∠OCN=∠ONC,∴∠OMD=∠ONE.∵∠ODC=∠OMD+∠MOD,∠CEO=∠ONE+∠NOE,∴∠MOD=∠NOE,∴=.
20.解:(1)∵△ABC是等边三角形,∴AC=AB,∠CAB=60°.由旋转的性质得AE=AD,∠EAD=∠CAB=60°,∴∠EAC=∠DAB.在△ACE和△ABD中,∴△ACE≌△ABD(SAS).
(2)∵CF⊥AB,AC=BC,∴CF垂直平分AB,∠ACF=∠ACB=30°,∴AD=DB,∴∠ABD=∠DAB=(180°-∠ADB)=20°.∵△ACE≌△ABD,∴∠ACE=∠ABD=20°,∴∠ECD=∠ACE+∠ACF=50°.
21.解:(1)连接OB.∴OA=OB,∴∠OBA=∠OAB=α=35°,∴∠AOB=180°-∠OAB-∠OBA=110°,∴β=∠C=∠AOB=55°.
(2)α与β之间的关系是α+β=90°.理由:∵OA=OB,∴∠OBA=∠OAB=α,∴∠AOB=180°-∠OAB-∠OBA=180°-2α,∴β=∠C=∠AOB=(180°-2α)=90°-α,
即α+β=90°.
22.解:(1)连接OB.∵OC⊥AB,∴D为AB的中点,∴BD=AB=6 m.设OB=OC=r,则OD=(r-4) m.在Rt△BOD中,根据勾股定理得r2=(r-4)2+62,解得r=6.5,∴拱桥的半径为6.5 m.
(2)∵CD=4 m,船舱顶部为长方形且高出水面3.6 m,∴CE=4-3.6=0.4(m),∴OE=r-CE=6.1(m).连接ON.在Rt△OEN中,EN== m,∴MN=2EN≈4.49 m<5 m,∴此货船不能顺利通过拱桥.
23.解:(1)∵四边形ABCD为矩形,∴∠A=∠D=90°,AB=DC.∵E是AD的中点,∴AE=DE,∴△ABE≌△DCE,∴BE=CE.
(2)①由(1)知△ABE≌△DCE,∴∠AEB=∠DEC,BE=CE.∵∠BEC=90°,∴∠AEB=∠DEC=45°,∴∠ABE=∠ECB=45°.∵∠BEM+∠BEN=∠CEN+∠BEN=90°,∴∠BEM=∠CEN.在△BEM和△CEN中,∴△BEM≌△CEN.②由①可知△ABE和△DEC都是等腰直角三角形,E为AD的中点,∴BC=AD=2AB=4.由①得△BEM≌△CEN,∴BM=CN.设BM=CN=x,则BN=4-x,∴S△BMN=BM·BN=x(4-x)=-(x-2)2+2,∴当x=2时, △BMN的面积最大,最大面积为2.③∵BC∥AD,∠FEG=90°,∴∠BNG=∠FEG=90°.∵∠F=30°,∴∠NBG=∠F=30°.由①可知∠EBN=45°.设NG=y,则BG=2y,BN=y,EN=y,∴BE=y,∴S△EBG=EB·BG·sin ∠EBG=EG·BN,∴sin ∠EBG===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆(24.1~24.3)】
本试卷共8大题,计23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A B C D
2.若正方形ABCD的四个顶点都在☉O上,则边AB所对的圆心角的度数是( )
A.45° B.90° C.120° D.135°
3.用反证法证明“是无理数”时,第一个步骤是先假设( )
A.是有理数 B.是整数 C.是分数 D.是实数
4.如图,若将边长为的正方形绕点B逆时针旋转30°,则图中阴影部分的面积为( )
A.3 B. C.3- D.3-
5.如图,☉A过点O(0,0),C(2,0),D(0,2),B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
6.如图,已知AB是☉O的直径,CD是☉O的弦,CD⊥AB,垂足为P.若BP∶AP=1∶5,CD=10,则☉O的半径长为( )
A.3 B.5 C.2 D.
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.已知EF=CD=16 cm,则球的半径为( )
A.10 cm B.8 cm C.10 cm D.10 cm
8.如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,将△ABC绕点A逆时针旋转得到△ADE,使得点D落在AC上,则tan ∠ECD的值为( )
A. B. C. D.
9.如图,四边形ABCD内接于☉O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin ∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
10.如图,在平面直角坐标系中,已知点P(2,4),点A(0,3),点B(4,0),C是AB的中点,将△OAB绕点O旋转一周,在旋转过程中,点P与点C距离的最小值为( )
A.-2 B.2-2.5 C.2-5 D.2.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.把点P(-6,8)绕坐标原点旋转180°后对应点的坐标为 .
12.如图,已知圆弧形桥拱的半径为10米,拱高CD=4米,那么圆弧形桥拱的跨度AB= 米.
13.如图,点A的坐标为(0,4),点B的坐标为(4,2),点C的坐标为(6,2),点D的坐标为(4,-2),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .
14.如图,四边形ABCD内接于☉O,对角线AC,BD交于点P,且AB=AD.若AC=7,AB=3,则
(1)AP= ;
(2)BC·CD= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,四边形ABCD内接于☉O,若∠BOD=160°,求∠C的度数.
16.如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上的三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位长度,使其落在△A1B1C1内部,指出h的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在☉O中,AB,AC为互相垂直且相等的两条弦,OD⊥AB于点D,OE⊥AC于点E.求证:四边形AEOD是正方形.
18.如图,在△AOB中,OA=OB=8,点C的坐标为(0,2),P是OB上一个动点,连接CP,将线段CP绕点C逆时针旋转90°得到线段CD,使点D恰好落在AB上.求点D的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在☉O中,C是优弧的中点,D,E分别是OA,OB上的点,且AD=BE,弦 CM,CN分别过点D,E.
(1)求证:CD=CE;
(2)求证:=.
20.如图,D是等边△ABC内一点,将线段AD绕点A逆时针旋转60°得到线段AE,连接CD并延长,交AB于点F,连接BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
六、(本题满分12分)
21.如图,△ABC是☉O的内接三角形,C是优弧上一点(点C不与点A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
七、(本题满分12分)
22.如图,有一座圆弧形拱桥,桥下水面宽度AB为12 m,拱高CD为4 m.
(1)求拱桥的半径;
(2)有一艘宽为5 m的货船,船舱顶部为长方形,且高出水面3.6 m,求此货船是否能顺利通过拱桥
八、(本题满分14分)
23.如图1,在矩形ABCD中,E是AD的中点,以E为直角顶点的直角△EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE.
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动,若EF,EG分别与AB,BC相交于点M,N(如图2).
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin ∠EBG的值.
参 考 答 案
1.D 2.B 3.A 4.C 5.B 6.A 7.D 8.B 9.C 10.B
11.(6,-8) 12.16 13.(2,0)或(5,3) 14.(1)40 (2)40
15.解:∵∠BOD=160°,∴∠A=∠BOD=80°.又∵∠A+∠C=180°,∴∠C=180°-∠A=100°.
16.解:(1)如图所示,△A1B1C1即为所求.
(2)点B2的坐标为(2,-1).观察可知,h的取值范围为2
18.解:过点D作DE⊥OA,垂足为E.∵线段CP绕点C逆时针旋转90°得到线段CD,∴CD=CP.∵∠PCD=90°,∴∠ECD+∠OCP=90°.又∵∠OPC+∠OCP=90°,∴∠OPC=∠ECD.在△OCP和△EDC中,∠OPC=∠ECD,∠COP=∠DEC,CD=CP,∴△OCP≌△EDC(AAS),∴DE=OC=2.∵OA=OB=8,∠AOB=90°,∴∠OAB=45°.∵DE⊥OA,∴∠DEA=90°,∴AE=DE=2,∴OE=OA-AE=8-2=6,∴点D的坐标为(2,6).
19.证明:(1)连接OC.由题意得=,∴∠COD=∠COE.∵OA=OB,AD=BE,∴OD=OE.又∵OC=OC,∴△COD≌△COE(SAS),∴CD=CE.
(2)连接OM,ON.由(1)得△COD≌△COE,∴∠ODC=∠OEC,∠OCD=∠OCE.∵OC=OM=ON,∴∠OCM=∠OMC,∠OCN=∠ONC,∴∠OMD=∠ONE.∵∠ODC=∠OMD+∠MOD,∠CEO=∠ONE+∠NOE,∴∠MOD=∠NOE,∴=.
20.解:(1)∵△ABC是等边三角形,∴AC=AB,∠CAB=60°.由旋转的性质得AE=AD,∠EAD=∠CAB=60°,∴∠EAC=∠DAB.在△ACE和△ABD中,∴△ACE≌△ABD(SAS).
(2)∵CF⊥AB,AC=BC,∴CF垂直平分AB,∠ACF=∠ACB=30°,∴AD=DB,∴∠ABD=∠DAB=(180°-∠ADB)=20°.∵△ACE≌△ABD,∴∠ACE=∠ABD=20°,∴∠ECD=∠ACE+∠ACF=50°.
21.解:(1)连接OB.∴OA=OB,∴∠OBA=∠OAB=α=35°,∴∠AOB=180°-∠OAB-∠OBA=110°,∴β=∠C=∠AOB=55°.
(2)α与β之间的关系是α+β=90°.理由:∵OA=OB,∴∠OBA=∠OAB=α,∴∠AOB=180°-∠OAB-∠OBA=180°-2α,∴β=∠C=∠AOB=(180°-2α)=90°-α,
即α+β=90°.
22.解:(1)连接OB.∵OC⊥AB,∴D为AB的中点,∴BD=AB=6 m.设OB=OC=r,则OD=(r-4) m.在Rt△BOD中,根据勾股定理得r2=(r-4)2+62,解得r=6.5,∴拱桥的半径为6.5 m.
(2)∵CD=4 m,船舱顶部为长方形且高出水面3.6 m,∴CE=4-3.6=0.4(m),∴OE=r-CE=6.1(m).连接ON.在Rt△OEN中,EN== m,∴MN=2EN≈4.49 m<5 m,∴此货船不能顺利通过拱桥.
23.解:(1)∵四边形ABCD为矩形,∴∠A=∠D=90°,AB=DC.∵E是AD的中点,∴AE=DE,∴△ABE≌△DCE,∴BE=CE.
(2)①由(1)知△ABE≌△DCE,∴∠AEB=∠DEC,BE=CE.∵∠BEC=90°,∴∠AEB=∠DEC=45°,∴∠ABE=∠ECB=45°.∵∠BEM+∠BEN=∠CEN+∠BEN=90°,∴∠BEM=∠CEN.在△BEM和△CEN中,∴△BEM≌△CEN.②由①可知△ABE和△DEC都是等腰直角三角形,E为AD的中点,∴BC=AD=2AB=4.由①得△BEM≌△CEN,∴BM=CN.设BM=CN=x,则BN=4-x,∴S△BMN=BM·BN=x(4-x)=-(x-2)2+2,∴当x=2时, △BMN的面积最大,最大面积为2.③∵BC∥AD,∠FEG=90°,∴∠BNG=∠FEG=90°.∵∠F=30°,∴∠NBG=∠F=30°.由①可知∠EBN=45°.设NG=y,则BG=2y,BN=y,EN=y,∴BE=y,∴S△EBG=EB·BG·sin ∠EBG=EG·BN,∴sin ∠EBG===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
