沪科版九年级下册数学阶段达标检测卷—第24章 圆(24.4~24.8)(含答案)
文档属性
| 名称 | 沪科版九年级下册数学阶段达标检测卷—第24章 圆(24.4~24.8)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 07:50:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆(24.4~24.8)】
本试卷共8大题,计23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点A(-2,3)绕坐标原点O逆时针旋转90°后对应的点A'的坐标是( )
A.(3,-2) B.(2,-3) C.(-2,-3) D.(-3,-2)
2.正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补 C.互余或互补 D.不能确定
3.如图,AB是☉O的切线,A为切点,连接OA,OB.若∠B=20°,则∠AOB的度数为( )
A.40° B.50° C.60° D.70°
4.如图,已知AB是☉O的直径,点C在☉O上,点D在半径OA上(不与点O,A重合).若∠COA=60°,∠CDO=70°,则∠ACD的度数是( )
A.10° B.30° C.50° D.60°
5.已知☉O的半径为10,弦AB的长为10,则弦AB所对的圆周角的度数是( )
A.30° B.60° C.30°或150° D.60°或120°
6.在Rt△ABC中,若∠C=90°,AC=6 cm,BC=8 cm,则△ABC的内切圆与外接圆的面积之比为( )
A.2∶5 B.3∶4 C.4∶25 D.9∶61
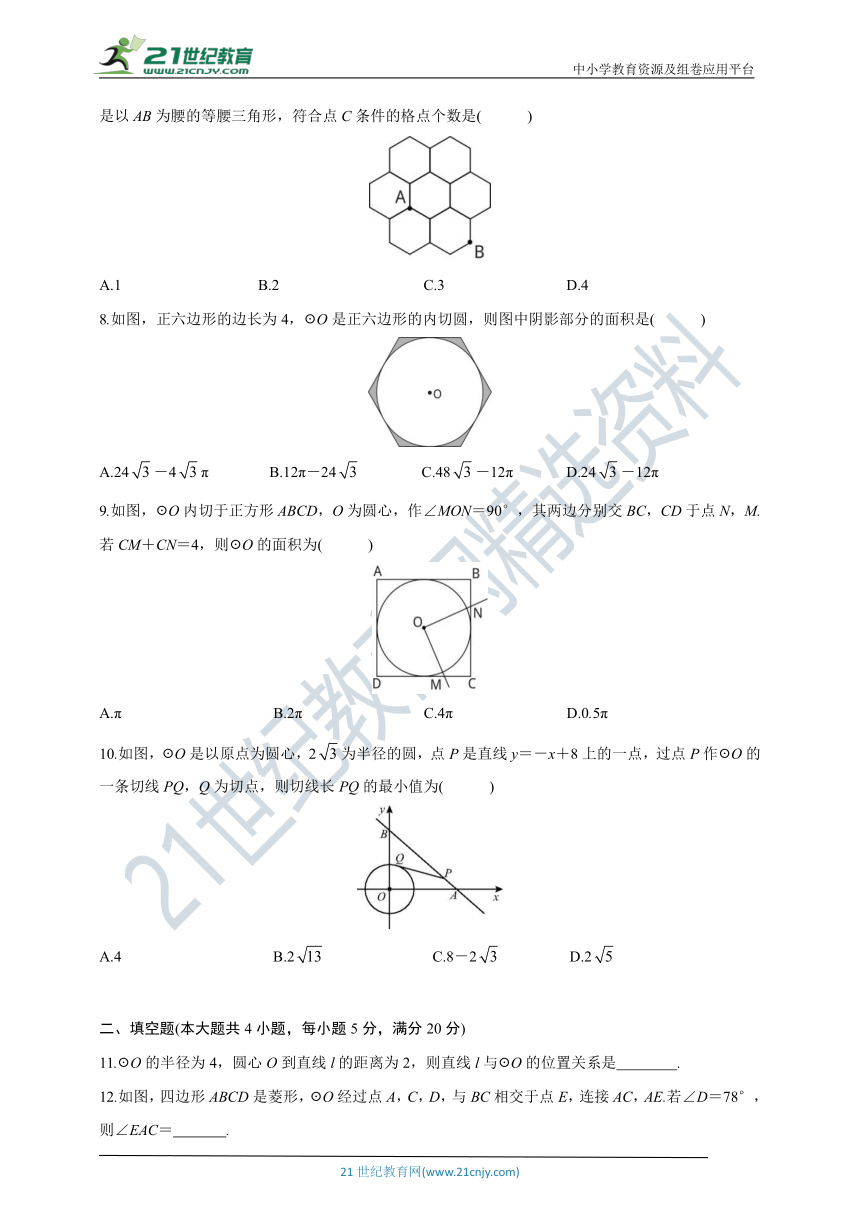
7.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( )
A.1 B.2 C.3 D.4
8.如图,正六边形的边长为4,☉O是正六边形的内切圆,则图中阴影部分的面积是( )
A.24-4π B.12π-24 C.48-12π D.24-12π
9.如图,☉O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M.若CM+CN=4,则☉O的面积为( )
A.π B.2π C.4π D.0.5π
10.如图,☉O是以原点为圆心,2为半径的圆,点P是直线y=-x+8上的一点,过点P作☉O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.4 B.2 C.8-2 D.2
二、填空题(本大题共4小题,每小题5分,满分20分)
11.☉O的半径为4,圆心O到直线l的距离为2,则直线l与☉O的位置关系是 .
12.如图,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=78°,则∠EAC= .
13.如图,☉O的内接正五边形ABCDE的对角线AD与BE相交于点G.若AE=2,则EG的长是 .
14.如图,四边形ABCD是☉O的内接四边形,四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.则
(1)∠A的度数为 ;
(2)当☉O的半径等于2时,的长为 .(结果保留π)
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知AB=AC,BD=CD,点D在BC上,以点A为圆心的圆恰好经过点D.求证:BC为☉A的切线.
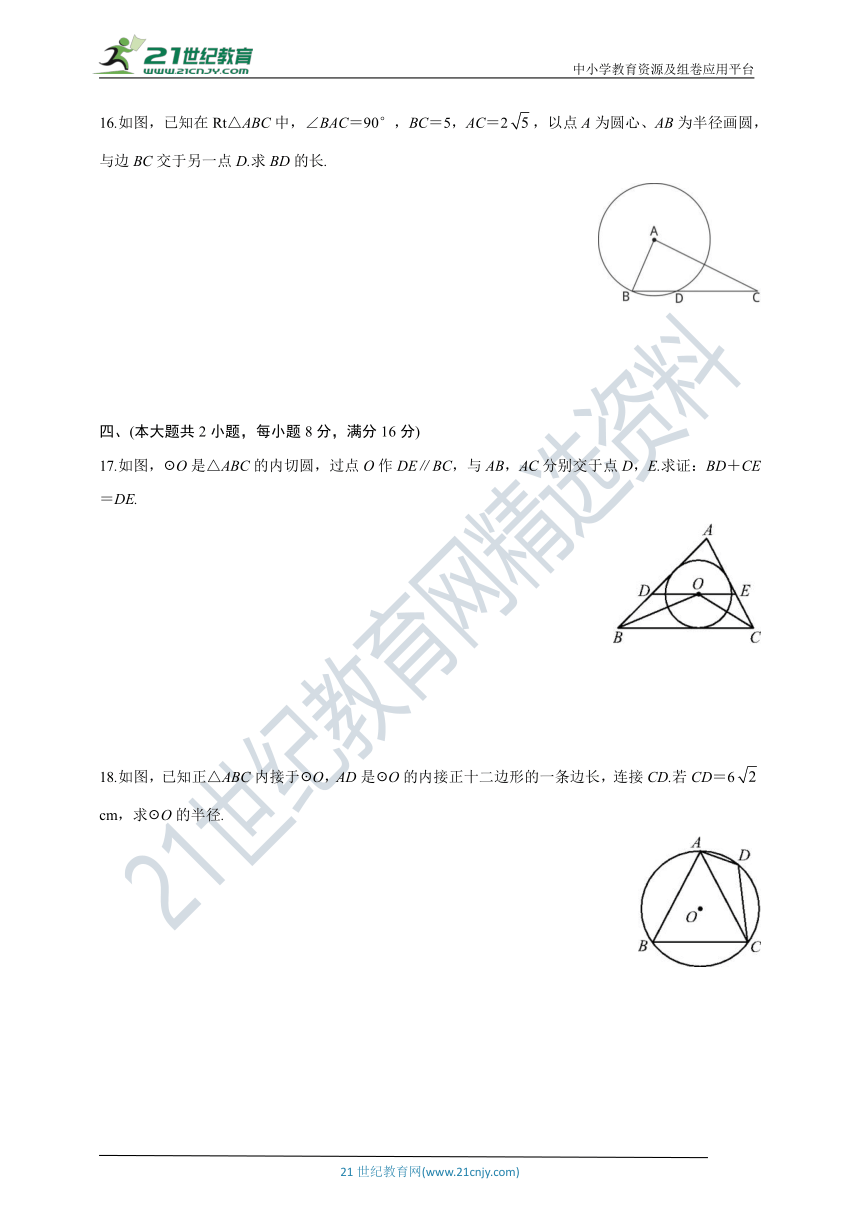
16.如图,已知在Rt△ABC中,∠BAC=90°,BC=5,AC=2,以点A为圆心、AB为半径画圆,与边BC交于另一点D.求BD的长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,☉O是△ABC的内切圆,过点O作DE∥BC,与AB,AC分别交于点D,E.求证:BD+CE=DE.
18.如图,已知正△ABC内接于☉O,AD是☉O的内接正十二边形的一条边长,连接CD.若CD=6 cm,求☉O的半径.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,△ABC内接于☉O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长,交过点A的切线于点G,且满足AG∥BC,连接OC,cos ∠BAC=.
(1)求证:∠COD=∠BAC;
(2)求证:CF是☉O的切线.
20.如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆☉O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是☉O的切线;
(2)若DF=2,AF=5,求BD的长.
六、(本题满分12分)
21.如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到线段AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
七、(本题满分12分)
22.如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于点D,E两点,过点D作DF⊥AC,垂足为F.
(1)判断DF与☉O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
八、(本题满分14分)
23.如图1,AB是☉O的直径,点O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.延长PD交☉O的切线BE于点E.
(1)试探究直线PD与☉O之间的位置关系,并说明理由;
(2)如果∠BED=60°,PD=,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在☉O上,如图2,求证:四边形DFBE为菱形.
参 考 答 案
1.D 2.B 3.D 4.A 5.D 6.C 7.B 8.D 9.C 10.D
11.相交 12.27° 13.-1 14.(1)45° (2)π
15.证明:连接AD.∵AB=AC,BD=CD,∴AD⊥BC.又∵AD是☉A的半径,∴BC为☉A的切线.
16.解:连接AD,过点A作AH⊥BD于点H.在Rt△ABC中,BC=5,AC=2,∴AB==.∵AB·AC=BC·AH,∴AH==2,∴BH==1.∵AH⊥BD,AB=AD,∴BH=HD=1,∴BD=2.
17.证明:∵☉O是△ABC的内切圆,∴BO平分∠ABC,CO平分∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB.∵DE∥BC,∴∠DOB=∠OBC,∠EOC=OCB,∴∠DBO=∠DOB,∠ECO=∠EOC,∴BD=DO,EO=EC,∴DE=DO+EO=BD+CE.
18.解:连接OA,OD,OC.∵正△ABC内接于☉O,AD为内接正十二边形的一边,∴∠AOC=×360°=120°,∠AOD=×360°=30°,∴∠COD=∠AOC-∠AOD=90°.∵OC=OD,∴△OCD是等腰直角三角形,∴OC=OD=CD=×6=6(cm),即☉O的半径为6 cm.
19.证明:(1)∵AG是☉O的切线,AD是☉O的直径,∴∠GAF=90°.∵AG∥BC,∴AE⊥BC,∴CE=BE,即AF为BC的垂直平分线,∴∠BAC=2∠DAC.∵∠COD=2∠DAC,∴∠COD=∠BAC.
(2)∵DF=2OD,∴OF=3OD=3OC.∵cos ∠BAC=,∴cos ∠COD===.又∵∠COE=∠FOC,∴△COE∽△FOC,∴∠OCF=∠OEC=90°,∴CF是☉O的切线.
20.解:(1)连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴=,∴OD⊥BC.
又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为☉O的半径,∴直线DM是☉O的切线.
(2)∵=,∴∠DBF=∠DAB.又∵∠BDF=∠ADB,∴△DBF∽△DAB,∴=,即BD2=DF·DA.∵DF=2,AF=5,∴DA=DF+AF=7,∴BD2=DF·DA=14,∴BD=.
21.解:(1)∵∠CAF=∠BAE,∴∠BAC=∠EAF.由旋转的性质可知AC=AF.在△ABC与△AEF中,∴△ABC≌△AEF(SAS),∴EF=BC.
(2)∵AB=AE,∠ABC=65°,∴∠BAE=180°-65°×2=50°,∴∠CAF=∠BAE=50°.由(1)知△ABC≌△AEF,∴∠F=∠C=28°,∴∠FGC=∠CAF+∠F=50°+28°=78°.
22.解:(1)DF与☉O相切.如图,连接OD.∵AC=BC,OB=OD,∴∠B=∠A,∠B=∠1,∴∠A=∠1,∴OD∥AC.∵DF⊥AC,∴∠AFD=90°,∴∠ODF=∠AFD=90°.又∵OD是☉O的半径,∴DF与☉O相切.
(2)如图,过点O作OG⊥EC于点G,连接OE.∵∠ODF=∠AFD=90°,∴四边形OGFD是矩形,∴DF=OG,FG=OD=OB=OC=BC=.∵OG⊥EC,∴CG=EG=FG-EF=-1=,∴DF=OG===2.
23.解:(1)直线PD为☉O的切线.理由:连接OD.∵AB是☉O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°.又∵DO=BO,∴∠BDO=∠PBD.∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即∠PDO=90°.∵点D在☉O上,∴直线PD为☉O的切线.
(2)∵BE是☉O的切线,∴∠EBA=90°.∵∠BED=60°,∴∠P=30°.∵PD为☉O的切线,∴∠PDO=90°.在Rt△PDO中,∠P=30°,PD=,∴OD=PD·tan 30°=1,OP==2,∴PA=PO-AO=2-1=1.
(3)依题意得∠ADF=∠PDA,∠PAD=∠DAF.∵∠PDA=∠PBD,∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF.∵AB是☉O的直径,∴∠ADB=90°.设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°.∵四边形AFBD内接于☉O,∴∠DAF+∠DBF=180°,∴90+x+2x=180,解得x=30,∴∠ADF=∠PDA=∠PBD=∠ABF=30°.∵BE,ED是☉O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE.又∵∠FDB=∠ADB-∠ADF=90°-30°=60°,∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆(24.4~24.8)】
本试卷共8大题,计23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点A(-2,3)绕坐标原点O逆时针旋转90°后对应的点A'的坐标是( )
A.(3,-2) B.(2,-3) C.(-2,-3) D.(-3,-2)
2.正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补 C.互余或互补 D.不能确定
3.如图,AB是☉O的切线,A为切点,连接OA,OB.若∠B=20°,则∠AOB的度数为( )
A.40° B.50° C.60° D.70°
4.如图,已知AB是☉O的直径,点C在☉O上,点D在半径OA上(不与点O,A重合).若∠COA=60°,∠CDO=70°,则∠ACD的度数是( )
A.10° B.30° C.50° D.60°
5.已知☉O的半径为10,弦AB的长为10,则弦AB所对的圆周角的度数是( )
A.30° B.60° C.30°或150° D.60°或120°
6.在Rt△ABC中,若∠C=90°,AC=6 cm,BC=8 cm,则△ABC的内切圆与外接圆的面积之比为( )
A.2∶5 B.3∶4 C.4∶25 D.9∶61
7.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( )
A.1 B.2 C.3 D.4
8.如图,正六边形的边长为4,☉O是正六边形的内切圆,则图中阴影部分的面积是( )
A.24-4π B.12π-24 C.48-12π D.24-12π
9.如图,☉O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M.若CM+CN=4,则☉O的面积为( )
A.π B.2π C.4π D.0.5π
10.如图,☉O是以原点为圆心,2为半径的圆,点P是直线y=-x+8上的一点,过点P作☉O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.4 B.2 C.8-2 D.2
二、填空题(本大题共4小题,每小题5分,满分20分)
11.☉O的半径为4,圆心O到直线l的距离为2,则直线l与☉O的位置关系是 .
12.如图,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=78°,则∠EAC= .
13.如图,☉O的内接正五边形ABCDE的对角线AD与BE相交于点G.若AE=2,则EG的长是 .
14.如图,四边形ABCD是☉O的内接四边形,四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.则
(1)∠A的度数为 ;
(2)当☉O的半径等于2时,的长为 .(结果保留π)
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知AB=AC,BD=CD,点D在BC上,以点A为圆心的圆恰好经过点D.求证:BC为☉A的切线.
16.如图,已知在Rt△ABC中,∠BAC=90°,BC=5,AC=2,以点A为圆心、AB为半径画圆,与边BC交于另一点D.求BD的长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,☉O是△ABC的内切圆,过点O作DE∥BC,与AB,AC分别交于点D,E.求证:BD+CE=DE.
18.如图,已知正△ABC内接于☉O,AD是☉O的内接正十二边形的一条边长,连接CD.若CD=6 cm,求☉O的半径.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,△ABC内接于☉O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长,交过点A的切线于点G,且满足AG∥BC,连接OC,cos ∠BAC=.
(1)求证:∠COD=∠BAC;
(2)求证:CF是☉O的切线.
20.如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆☉O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是☉O的切线;
(2)若DF=2,AF=5,求BD的长.
六、(本题满分12分)
21.如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到线段AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
七、(本题满分12分)
22.如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于点D,E两点,过点D作DF⊥AC,垂足为F.
(1)判断DF与☉O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
八、(本题满分14分)
23.如图1,AB是☉O的直径,点O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.延长PD交☉O的切线BE于点E.
(1)试探究直线PD与☉O之间的位置关系,并说明理由;
(2)如果∠BED=60°,PD=,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在☉O上,如图2,求证:四边形DFBE为菱形.
参 考 答 案
1.D 2.B 3.D 4.A 5.D 6.C 7.B 8.D 9.C 10.D
11.相交 12.27° 13.-1 14.(1)45° (2)π
15.证明:连接AD.∵AB=AC,BD=CD,∴AD⊥BC.又∵AD是☉A的半径,∴BC为☉A的切线.
16.解:连接AD,过点A作AH⊥BD于点H.在Rt△ABC中,BC=5,AC=2,∴AB==.∵AB·AC=BC·AH,∴AH==2,∴BH==1.∵AH⊥BD,AB=AD,∴BH=HD=1,∴BD=2.
17.证明:∵☉O是△ABC的内切圆,∴BO平分∠ABC,CO平分∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB.∵DE∥BC,∴∠DOB=∠OBC,∠EOC=OCB,∴∠DBO=∠DOB,∠ECO=∠EOC,∴BD=DO,EO=EC,∴DE=DO+EO=BD+CE.
18.解:连接OA,OD,OC.∵正△ABC内接于☉O,AD为内接正十二边形的一边,∴∠AOC=×360°=120°,∠AOD=×360°=30°,∴∠COD=∠AOC-∠AOD=90°.∵OC=OD,∴△OCD是等腰直角三角形,∴OC=OD=CD=×6=6(cm),即☉O的半径为6 cm.
19.证明:(1)∵AG是☉O的切线,AD是☉O的直径,∴∠GAF=90°.∵AG∥BC,∴AE⊥BC,∴CE=BE,即AF为BC的垂直平分线,∴∠BAC=2∠DAC.∵∠COD=2∠DAC,∴∠COD=∠BAC.
(2)∵DF=2OD,∴OF=3OD=3OC.∵cos ∠BAC=,∴cos ∠COD===.又∵∠COE=∠FOC,∴△COE∽△FOC,∴∠OCF=∠OEC=90°,∴CF是☉O的切线.
20.解:(1)连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴=,∴OD⊥BC.
又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为☉O的半径,∴直线DM是☉O的切线.
(2)∵=,∴∠DBF=∠DAB.又∵∠BDF=∠ADB,∴△DBF∽△DAB,∴=,即BD2=DF·DA.∵DF=2,AF=5,∴DA=DF+AF=7,∴BD2=DF·DA=14,∴BD=.
21.解:(1)∵∠CAF=∠BAE,∴∠BAC=∠EAF.由旋转的性质可知AC=AF.在△ABC与△AEF中,∴△ABC≌△AEF(SAS),∴EF=BC.
(2)∵AB=AE,∠ABC=65°,∴∠BAE=180°-65°×2=50°,∴∠CAF=∠BAE=50°.由(1)知△ABC≌△AEF,∴∠F=∠C=28°,∴∠FGC=∠CAF+∠F=50°+28°=78°.
22.解:(1)DF与☉O相切.如图,连接OD.∵AC=BC,OB=OD,∴∠B=∠A,∠B=∠1,∴∠A=∠1,∴OD∥AC.∵DF⊥AC,∴∠AFD=90°,∴∠ODF=∠AFD=90°.又∵OD是☉O的半径,∴DF与☉O相切.
(2)如图,过点O作OG⊥EC于点G,连接OE.∵∠ODF=∠AFD=90°,∴四边形OGFD是矩形,∴DF=OG,FG=OD=OB=OC=BC=.∵OG⊥EC,∴CG=EG=FG-EF=-1=,∴DF=OG===2.
23.解:(1)直线PD为☉O的切线.理由:连接OD.∵AB是☉O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°.又∵DO=BO,∴∠BDO=∠PBD.∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即∠PDO=90°.∵点D在☉O上,∴直线PD为☉O的切线.
(2)∵BE是☉O的切线,∴∠EBA=90°.∵∠BED=60°,∴∠P=30°.∵PD为☉O的切线,∴∠PDO=90°.在Rt△PDO中,∠P=30°,PD=,∴OD=PD·tan 30°=1,OP==2,∴PA=PO-AO=2-1=1.
(3)依题意得∠ADF=∠PDA,∠PAD=∠DAF.∵∠PDA=∠PBD,∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF.∵AB是☉O的直径,∴∠ADB=90°.设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°.∵四边形AFBD内接于☉O,∴∠DAF+∠DBF=180°,∴90+x+2x=180,解得x=30,∴∠ADF=∠PDA=∠PBD=∠ABF=30°.∵BE,ED是☉O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE.又∵∠FDB=∠ADB-∠ADF=90°-30°=60°,∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
