沪科版九年级下册数学阶段达标检测卷—第24章 圆(含答案)
文档属性
| 名称 | 沪科版九年级下册数学阶段达标检测卷—第24章 圆(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 08:19:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下面四个手机应用图标中,属于中心对称图形的是( )
A B C D
2.以圆为弧的扇形的圆心角的度数是( )
A.45° B.60° C.90° D.120°
3.在△ABC中,AC=3,CB=4,以点C为圆心、r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
A.r>3 B.r≥4 C.34.如图,☉O的直径BA的延长线与弦DC的延长线交于点E,且CE=OB.已知∠DOB=72°,则∠E的度数是( )
A.36° B.30° C.24° D.18°
5.如果正十边形的边长为a,那么它的外接圆半径是( )
A. B. C. D.
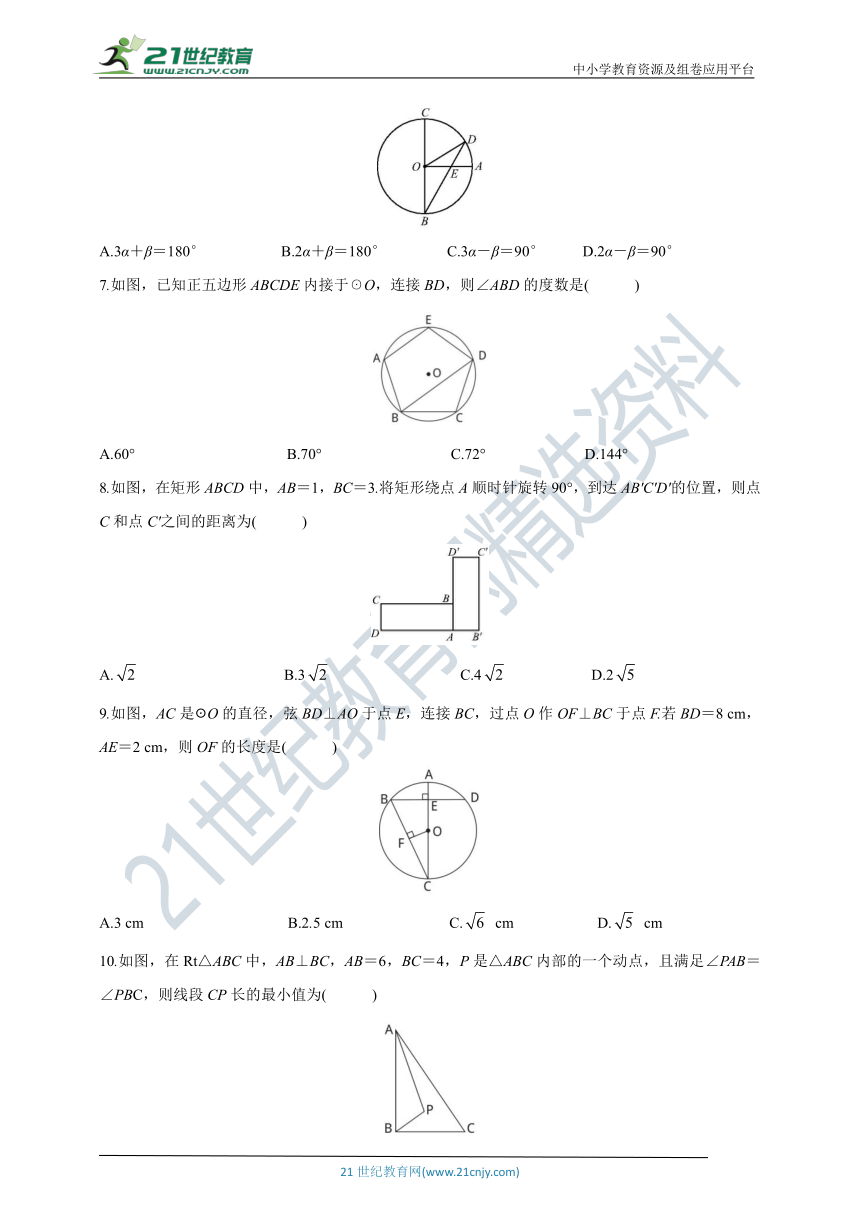
6.如图,已知BC是☉O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
7.如图,已知正五边形ABCDE内接于☉O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
8.如图,在矩形ABCD中,AB=1,BC=3.将矩形绕点A顺时针旋转90°,到达AB'C'D'的位置,则点C和点C'之间的距离为( )
A. B.3 C.4 D.2
9.如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F.若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B.2.5 cm C. cm D. cm
10.如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.用反证法证明“在△ABC中,AB=AC,则∠B必为锐角”的第一步是假设 .
12.如图,☉O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE= .
13.如图,已知☉O的直径AB=8,点C在☉O上,∠CAB=22.5°,过点C作CD⊥AB交☉O于点D,则的长为 .
14.如图,在☉O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.则
(1)AB CD(填“>”“=”或“<”);
(2)若☉O的半径为5,DE=1,则AE的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,D,E分别是,的中点,DE交AB于点M,交AC于点N.求证:∠AMN=∠ANM.
16.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°.若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin 41.3°≈0.66,cos 41.3°≈0.75,tan 41.3°≈0.88)
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心点M的坐标.
18.如图,正△ABC内接于☉O,若AB=4 cm,求☉O的直径及△ABC的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的☉O经过点C,交AB于点E,且AC=AE,CF为☉O的直径,连接FE并延长交BC于点G,连接AF.
(1)求证:四边形ADGF是平行四边形;
(2)若=,BE=4,求☉O的直径.
20.如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆☉O的直径是6,求BD的长.
六、(本题满分12分)
21.如图,线段AB为☉O的直径,点C,E在☉O上,=,CD⊥AB,垂足为D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos ∠ABE=,在AB的延长线上取一点M,使BM=4,☉O的半径为6.求证:直线CM是☉O的切线.
七、(本题满分12分)
22.如图,在△ABC中,∠ABC=90°,∠ACB=60°,将△ABC绕点C逆时针旋转60°得到△DGC,再将△ABC沿AB所在直线翻折得到△ABE,连接AD,BG,延长BG交AD于点F,连接CF.
(1)求证:四边形ABCF是矩形;
(2)若GF=2,求四边形AECD的面积.
八、(本题满分14分)
23.如图,☉O是△ABC的外接圆,AC是直径,OF∥AB,过点B作☉O的切线DE,与CA的延长线交于点D,与OF的延长线交于点E.
(1)求证:△ABD∽△BCD;
(2)若∠C=30°, 求证:△OED是等腰三角形;
(3)若☉O的半径为3,cos D=,求OF的长.
参 考 答 案
1.B 2. C 3. C 4.C 5. C 6.D 7.C 8.D 9. C 10.B
11.∠B一定不是锐角(是直角或钝角) 12.110° 13.2π 14.(1)= (2)7
15.证明:连接DO,EO.∵D是的中点,E是的中点,∴OD⊥AB,OE⊥AC,∴∠DMB=180°-90°-∠EDO,∠ENC=180°-90°-∠DEO.∵OD=OE,∴∠EDO=∠DEO,∴∠DMB=∠ENC.又∵∠DMB=∠AMN,∠ENC=∠ANM,∴∠AMN=∠ANM.
16.解:连接CO并延长,交AB于点D,则CD⊥AB,∴D为AB的中点,所求运行轨道的最高点C到弦AB所在直线的距离即为线段CD的长.在Rt△AOD中,∵AD=AB=3,∠OAD=41.3°,∴OD=AD·tan 41.3°≈3×0.88=2.64,AO=≈=4,∴CD=CO+OD=AO+OD=4+2.64=6.64(米).答:运行轨道的最高点C到弦AB所在直线的距离约为6.64米.
17.解:(1)①如图所示,△A1B1C1即为所求.
②如图所示,△A2B2C2即为所求.
(2)对称中心点M的坐标为(2,1).
18.解:如图,连接CO并延长交AB于点D,连接AO并延长交BC于点E.∵点O是正△ABC的外心,∴CD⊥AB,AE⊥BC,∠EAD=30°.设OD=x,则AO=2x,AD=AB=2.根据勾股定理得4x2-x2=(2)2,解得x=2,则2x=4,∴AO=4 cm,☉O的直径为8 cm,∴CD=AE=AB·sin 60°=6,∴S△ABC=AB·CD=×4×6=12.
19.解:(1)连接CE.∵AC=AE,∴=,∴AD⊥CE.∵CF是直径,∴∠CEF=90°,∴FG⊥CE,∴AD∥FG.∵CF,AD是直径,∴∠ACD=∠CAF=90°,∴AF∥BC,∴四边形ADGF是平行四边形.
(2)∵∠AOF=∠COD,∴=,∴AF=CD.∵四边形ADGF是平行四边形,∴AF=DG.∵=,∴=.∵EG∥AD,∴==.∵BE=4,∴AE=AC=6,∴AB=10,BC===8.∵CD=DG,=,∴CD=DG=3,∴AD===3.
20.解:(1)∵点E是△ABC的内心,∴∠BAD=∠CAD,∠ABE=∠CBE.∵∠CBD=∠CAD,∴∠BAD=∠CBD.∵∠BED=∠ABE+∠BAD,∴∠BED=∠CBE+∠CBD,即∠BED=∠EBD,∴ED=BD.(2)连接CD.∵∠BAC=90°,∴BC是☉O的直径,∴∠BDC=90°.∵☉O的直径为6,∴BC=6.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD=DC,∴BD=DC=BC=3.
21.证明:(1)延长CD交☉O于点G.∵CD⊥AB,∴=.∵=,∴=,
∴∠CBE=∠GCB,∴CF=BF.
(2)连接OC,交BE于点H.∵=,∴OC⊥BE.在Rt△OBH中,cos ∠OBH==,∴BH=×6=,∴OH===.∵==,==,∴=.∵∠HOB=∠COM,∴△OHB∽△OCM,∴∠OCM=∠OHB=90°,∴OC⊥CM,∴直线CM是☉O的切线.
22.解:(1)∵将△ABC绕点C旋转得到△DGC,∴AC=CD,∠DCG=∠ACB=60°,CG=CB,∴△ACD,△CBG均是等边三角形,∴∠DAC=60°,∠CGB=∠AGF=60°,BG=BC=CG,∴△AFG是等边三角形,∴AG=FG.∵∠ABC=90°,∠ACB=60°,∴AC=2BC,且BC=CG,∴AG=CG,∴AG=BG=FG=CG,∴四边形ABCF是平行四边形,且∠ABC=90°,∴四边形ABCF是矩形.
(2)∵将△ABC绕点C旋转得到△DGC,△ABC沿AB所在直线翻折得到△ABE,∠ABC=90°,∠ACB=60°,∴DC=AC=AE,∠DCG=∠ACB=∠AEC=60°,∴∠AEC+∠DCE=180°,∴DC∥AE.由(1)知四边形ABCF是矩形,∴AD∥CE,∴四边形AECD为平行四边形.又∵AC=2CB,∴AC=CE=AE,∴四边形AECD为菱形.∵GF=2,∴AC=CE=4,CB=2,在Rt△ABC中,AB===6,∴S四边形AECD=4×6=24.
23.解:(1)连接BO.∵BD是☉O的切线,∴∠OBD=90°,∴∠OBA+∠ABD=90°.∵AC是☉O的直径,∴∠ABC=∠CBO+∠OBA=90°,∴∠ABD=∠CBO.∵OB=OC,∴∠CBO=∠C,∴∠ABD=∠C.又∵∠D=∠D,∴△ABD∽△BCD.
(2)∵∠C=30°,OE∥AB,∠ABC=90°,∴∠BAO=60°=∠BOA=∠BOE.由(1)可知OB⊥DE,∴△BOE≌△BOD,∴OE=OD,即 △OED是等腰三角形.
(3)∵OE∥AB, CO=AO,∴CF=BF,∴OF是△ABC的中位线,∴OF=AB.在Rt△OBD中,cos D==,设BD=4x,则OD=5x.根据勾股定理得(5x)2=(4x)2+32,解得x=1,
∴BD=4,OD=5.过点B作BM⊥OA,垂足为M,∴△OBM∽△ODB,∴==,即==,∴BM=,OM=,∴AM=,∴AB==,∴OF=AB=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学阶段达标检测卷
【检测内容:第24章 圆】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下面四个手机应用图标中,属于中心对称图形的是( )
A B C D
2.以圆为弧的扇形的圆心角的度数是( )
A.45° B.60° C.90° D.120°
3.在△ABC中,AC=3,CB=4,以点C为圆心、r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
A.r>3 B.r≥4 C.3
A.36° B.30° C.24° D.18°
5.如果正十边形的边长为a,那么它的外接圆半径是( )
A. B. C. D.
6.如图,已知BC是☉O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
7.如图,已知正五边形ABCDE内接于☉O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
8.如图,在矩形ABCD中,AB=1,BC=3.将矩形绕点A顺时针旋转90°,到达AB'C'D'的位置,则点C和点C'之间的距离为( )
A. B.3 C.4 D.2
9.如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F.若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B.2.5 cm C. cm D. cm
10.如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.用反证法证明“在△ABC中,AB=AC,则∠B必为锐角”的第一步是假设 .
12.如图,☉O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE= .
13.如图,已知☉O的直径AB=8,点C在☉O上,∠CAB=22.5°,过点C作CD⊥AB交☉O于点D,则的长为 .
14.如图,在☉O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.则
(1)AB CD(填“>”“=”或“<”);
(2)若☉O的半径为5,DE=1,则AE的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,D,E分别是,的中点,DE交AB于点M,交AC于点N.求证:∠AMN=∠ANM.
16.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°.若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin 41.3°≈0.66,cos 41.3°≈0.75,tan 41.3°≈0.88)
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心点M的坐标.
18.如图,正△ABC内接于☉O,若AB=4 cm,求☉O的直径及△ABC的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的☉O经过点C,交AB于点E,且AC=AE,CF为☉O的直径,连接FE并延长交BC于点G,连接AF.
(1)求证:四边形ADGF是平行四边形;
(2)若=,BE=4,求☉O的直径.
20.如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆☉O的直径是6,求BD的长.
六、(本题满分12分)
21.如图,线段AB为☉O的直径,点C,E在☉O上,=,CD⊥AB,垂足为D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos ∠ABE=,在AB的延长线上取一点M,使BM=4,☉O的半径为6.求证:直线CM是☉O的切线.
七、(本题满分12分)
22.如图,在△ABC中,∠ABC=90°,∠ACB=60°,将△ABC绕点C逆时针旋转60°得到△DGC,再将△ABC沿AB所在直线翻折得到△ABE,连接AD,BG,延长BG交AD于点F,连接CF.
(1)求证:四边形ABCF是矩形;
(2)若GF=2,求四边形AECD的面积.
八、(本题满分14分)
23.如图,☉O是△ABC的外接圆,AC是直径,OF∥AB,过点B作☉O的切线DE,与CA的延长线交于点D,与OF的延长线交于点E.
(1)求证:△ABD∽△BCD;
(2)若∠C=30°, 求证:△OED是等腰三角形;
(3)若☉O的半径为3,cos D=,求OF的长.
参 考 答 案
1.B 2. C 3. C 4.C 5. C 6.D 7.C 8.D 9. C 10.B
11.∠B一定不是锐角(是直角或钝角) 12.110° 13.2π 14.(1)= (2)7
15.证明:连接DO,EO.∵D是的中点,E是的中点,∴OD⊥AB,OE⊥AC,∴∠DMB=180°-90°-∠EDO,∠ENC=180°-90°-∠DEO.∵OD=OE,∴∠EDO=∠DEO,∴∠DMB=∠ENC.又∵∠DMB=∠AMN,∠ENC=∠ANM,∴∠AMN=∠ANM.
16.解:连接CO并延长,交AB于点D,则CD⊥AB,∴D为AB的中点,所求运行轨道的最高点C到弦AB所在直线的距离即为线段CD的长.在Rt△AOD中,∵AD=AB=3,∠OAD=41.3°,∴OD=AD·tan 41.3°≈3×0.88=2.64,AO=≈=4,∴CD=CO+OD=AO+OD=4+2.64=6.64(米).答:运行轨道的最高点C到弦AB所在直线的距离约为6.64米.
17.解:(1)①如图所示,△A1B1C1即为所求.
②如图所示,△A2B2C2即为所求.
(2)对称中心点M的坐标为(2,1).
18.解:如图,连接CO并延长交AB于点D,连接AO并延长交BC于点E.∵点O是正△ABC的外心,∴CD⊥AB,AE⊥BC,∠EAD=30°.设OD=x,则AO=2x,AD=AB=2.根据勾股定理得4x2-x2=(2)2,解得x=2,则2x=4,∴AO=4 cm,☉O的直径为8 cm,∴CD=AE=AB·sin 60°=6,∴S△ABC=AB·CD=×4×6=12.
19.解:(1)连接CE.∵AC=AE,∴=,∴AD⊥CE.∵CF是直径,∴∠CEF=90°,∴FG⊥CE,∴AD∥FG.∵CF,AD是直径,∴∠ACD=∠CAF=90°,∴AF∥BC,∴四边形ADGF是平行四边形.
(2)∵∠AOF=∠COD,∴=,∴AF=CD.∵四边形ADGF是平行四边形,∴AF=DG.∵=,∴=.∵EG∥AD,∴==.∵BE=4,∴AE=AC=6,∴AB=10,BC===8.∵CD=DG,=,∴CD=DG=3,∴AD===3.
20.解:(1)∵点E是△ABC的内心,∴∠BAD=∠CAD,∠ABE=∠CBE.∵∠CBD=∠CAD,∴∠BAD=∠CBD.∵∠BED=∠ABE+∠BAD,∴∠BED=∠CBE+∠CBD,即∠BED=∠EBD,∴ED=BD.(2)连接CD.∵∠BAC=90°,∴BC是☉O的直径,∴∠BDC=90°.∵☉O的直径为6,∴BC=6.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD=DC,∴BD=DC=BC=3.
21.证明:(1)延长CD交☉O于点G.∵CD⊥AB,∴=.∵=,∴=,
∴∠CBE=∠GCB,∴CF=BF.
(2)连接OC,交BE于点H.∵=,∴OC⊥BE.在Rt△OBH中,cos ∠OBH==,∴BH=×6=,∴OH===.∵==,==,∴=.∵∠HOB=∠COM,∴△OHB∽△OCM,∴∠OCM=∠OHB=90°,∴OC⊥CM,∴直线CM是☉O的切线.
22.解:(1)∵将△ABC绕点C旋转得到△DGC,∴AC=CD,∠DCG=∠ACB=60°,CG=CB,∴△ACD,△CBG均是等边三角形,∴∠DAC=60°,∠CGB=∠AGF=60°,BG=BC=CG,∴△AFG是等边三角形,∴AG=FG.∵∠ABC=90°,∠ACB=60°,∴AC=2BC,且BC=CG,∴AG=CG,∴AG=BG=FG=CG,∴四边形ABCF是平行四边形,且∠ABC=90°,∴四边形ABCF是矩形.
(2)∵将△ABC绕点C旋转得到△DGC,△ABC沿AB所在直线翻折得到△ABE,∠ABC=90°,∠ACB=60°,∴DC=AC=AE,∠DCG=∠ACB=∠AEC=60°,∴∠AEC+∠DCE=180°,∴DC∥AE.由(1)知四边形ABCF是矩形,∴AD∥CE,∴四边形AECD为平行四边形.又∵AC=2CB,∴AC=CE=AE,∴四边形AECD为菱形.∵GF=2,∴AC=CE=4,CB=2,在Rt△ABC中,AB===6,∴S四边形AECD=4×6=24.
23.解:(1)连接BO.∵BD是☉O的切线,∴∠OBD=90°,∴∠OBA+∠ABD=90°.∵AC是☉O的直径,∴∠ABC=∠CBO+∠OBA=90°,∴∠ABD=∠CBO.∵OB=OC,∴∠CBO=∠C,∴∠ABD=∠C.又∵∠D=∠D,∴△ABD∽△BCD.
(2)∵∠C=30°,OE∥AB,∠ABC=90°,∴∠BAO=60°=∠BOA=∠BOE.由(1)可知OB⊥DE,∴△BOE≌△BOD,∴OE=OD,即 △OED是等腰三角形.
(3)∵OE∥AB, CO=AO,∴CF=BF,∴OF是△ABC的中位线,∴OF=AB.在Rt△OBD中,cos D==,设BD=4x,则OD=5x.根据勾股定理得(5x)2=(4x)2+32,解得x=1,
∴BD=4,OD=5.过点B作BM⊥OA,垂足为M,∴△OBM∽△ODB,∴==,即==,∴BM=,OM=,∴AM=,∴AB==,∴OF=AB=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
