沪科版九年级下册数学阶段达标检测卷—期中卷(含答案)
文档属性
| 名称 | 沪科版九年级下册数学阶段达标检测卷—期中卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
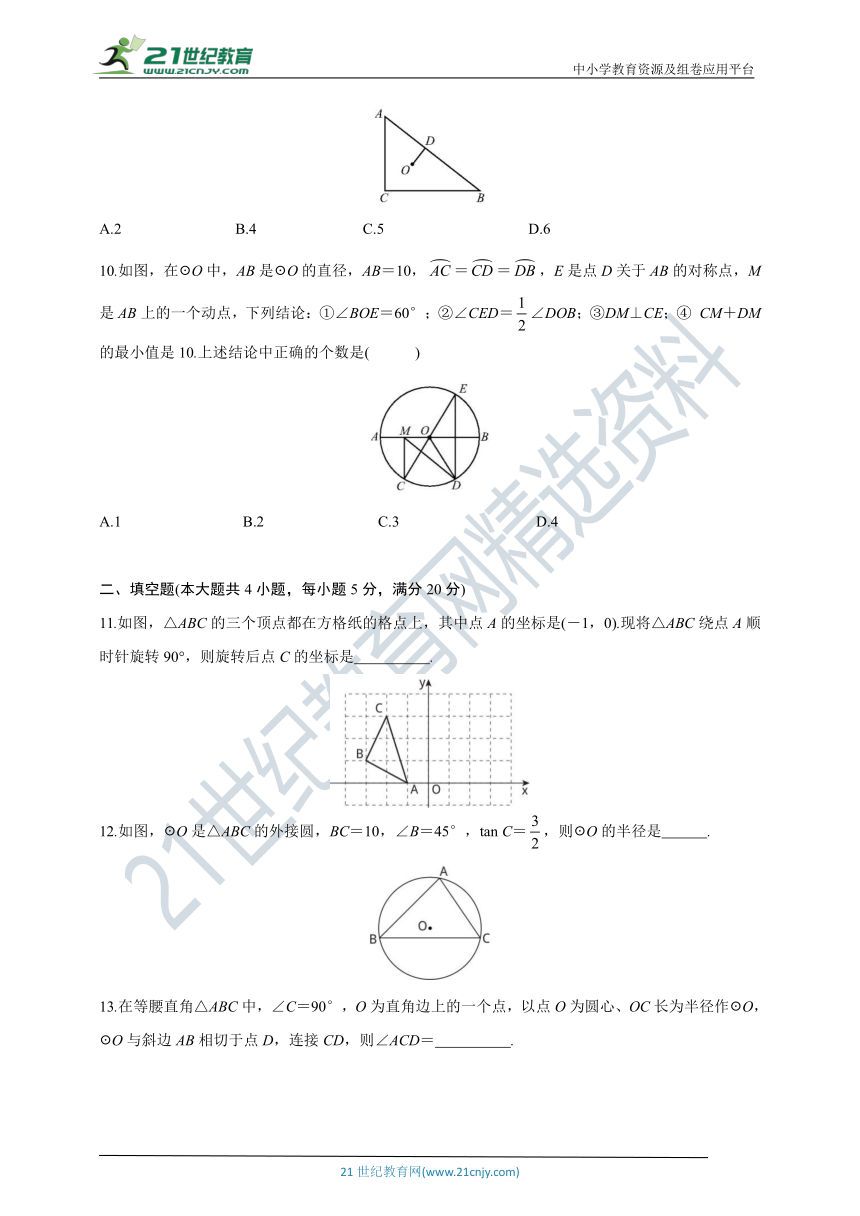
沪科版九年级下册数学期中达标检测卷
【检测内容:第24章 圆】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.如图,AB,AC是圆的两条弦,AD是圆的一条直径,且AD平分∠BAC.下列结论不一定正确的是( )
A.= B.= C.BC⊥AD D.∠B=∠C
3.如图,四边形ABCD内接于☉O,E为BC延长线上的一个点.若∠A=n°,则∠DCE的度数为( )
A.(180-n)° B.n° C.(90-n)° D.(90+n)°
4.如图,在☉O中,=,∠BAC=50°,则∠AEC的度数为( )
A.65° B.75° C.50° D.55°
5.如图,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EF6.如图,在平面直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA'B'C',再作图形OA'B'C'关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2) C.(-2,1) D.(-2,-1)
7.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
A. B. C. D.
8.如图,☉O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65° B.60° C.58° D.50°
9.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于点D,则AD的长为( )
A.2 B.4 C.5 D.6
10.如图,在☉O中,AB是☉O的直径,AB=10,==,E是点D关于AB的对称点,M是AB上的一个动点,下列结论:①∠BOE=60°;②∠CED=∠DOB;③DM⊥CE;④ CM+DM的最小值是10.上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是 .
12.如图,☉O是△ABC的外接圆,BC=10,∠B=45°,tan C=,则☉O的半径是 .
13.在等腰直角△ABC中,∠C=90°,O为直角边上的一个点,以点O为圆心、OC长为半径作☉O,☉O与斜边AB相切于点D,连接CD,则∠ACD= .
14.如图,在△ABC中,∠ACB=90°,sin ∠A=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A'B'上的动点,以点P为圆心、PA'长为半径作☉P.
(1)当☉P与△ABC的边AC相切时,☉P的半径为 ;
(2)当☉P与△ABC的边AB相切时,☉P的周长为 .
三、(本大题共2小题,每小题8分,满分16分)
15.在平面直角坐标系中,有三点A(-1,-1),P(0,-1),Q(-2,0),若以点A为圆心、OA长为半径作圆,试判断点P,Q与☉A的位置关系.
16.如图,AB是☉O的直径,E为BC的中点,AB=4,∠BED=120°,求图中阴影部分的面积.
四、(本大题共2小题,每小题8分,满分16分)
17.如果从半径为5 cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.
18.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点的坐标分别为A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心顺时针旋转90°,得到△A1B1C,请画出△A1B1C;
(2)平移△A1B1C,使点A1的对应点A2的坐标为(2,0),请画出平移后对应的△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,△ABC内接于☉O,AB为☉O的直径,AB=10,AC=6,连接OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
20.如图,已知AB是☉O的直径,C是圆上一点(不与点A,B重合).
(1)用尺规过点C作AB的垂线,交☉O于点D;(保留作图痕迹,不写作法)
(2)若AC=4,BC=2,求(1)中所作的弦CD的长.
六、(本题满分12分)
21.如图,AB是☉O的直径,C为的中点,CF为☉O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
七、(本题满分12分)
22.如图,已知在圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
(1)求∠ADB与∠ADC的大小;
(2)求证:AD=BD+CD.
八、(本题满分14分)
23.如图,四边形ABCD是☉O的内接四边形,线段AB是☉O的直径,连接AC,BD.H是线段BD上的一点,连接AH,CH且∠ACH=∠CBD,AD=CH,BA的延长线与CD的延长线相交于点P.
(1)求证:四边形ADCH是平行四边形.
(2)若AC=BC,PB=PD,AB+CD=2(+1),
①求证:△DHC为等腰直角三角形;
②求CH的长度.
参 考 答 案
1.A 2.A 3.B 4.A 5.C 6. A 7.B 8.B 9.B 10.C
11.(2,1) 12. 13.67.5°或22.5° 提示:∵△ABC为等腰直角三角形,∴∠A=∠B=45°,∠ACB=90°.①如图,当点O在BC上时,∵☉O与斜边AB相切于点D,∴OD⊥AB,∴∠BOD=45°.由圆周角定理得∠BCD=∠BOD=22.5°,∴∠ACD=90°-22.5°=67.5°.②如图,当点O'在AC上时,∵☉O'与斜边AB相切于点D',∴O'D'⊥AB,∴∠AO'D'=45°.由圆周角定理得∠ACD'=∠AO'D'=22.5°.综上所述,∠ACD=67.5°或22.5°.
14.(1) (2)
15.解:∵点A(-1,-1),P(0,-1),Q(-2,0),∴OA==,AP=1,AQ==,即AP16.解:连接AE,OD,OE.∵AB是☉O的直径,∴∠AEB=90°.又∵∠BED=120°,∴∠AED=30°,∴∠AOD=2∠AED=60°.∵OA=OD,∴△AOD是等边三角形,∴∠OAD=60°.∵E为BC的中点,∠AEB=90°,∴AB=AC,∴△ABC是等边三角形,边长是4,△EDC是等边三角形,边长是2,∴∠BOE=∠EOD=60°,∴和弦BE围成部分的面积等于和弦DE围成部分的面积,∴阴影部分的面积为S△EDC=×2×=.
17.解:∵从半径为5 cm的圆形纸片上剪去圆周的一个扇形,∴留下的扇形的弧长为=8π(cm).根据圆锥底面圆的周长等于扇形弧长,∴圆锥的底面半径r==4(cm),∴圆锥的高为=3(cm).
18.解:(1)如图所示,△A1B1C即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)如图所示,旋转中心的坐标为(-1,-1).
19.解:(1)∵AE=DE,OC是半径,∴=,∴∠CAD=∠CBA.
(2)∵AB是直径,∴∠ACB=90°.∵AE=DE,∴OC⊥AD,∴∠AEC=90°.∴∠AEC=∠ACB.由(1)知∠CAE=∠ABC,∴△AEC∽△BCA,∴=,即=,解得CE=3.6.∵OC=AB=5,∴OE=OC-EC=5-3.6=1.4.
20.解:(1)作图如图所示.
(2)∵AB是☉O的直径,∴∠ACB=90°,∴AB===2.∵S△ABC=AC·BC=AB·CE,∴CE==,∴CD=2CE=.
21.解:(1)∵C为的中点,∴=.∵AB是☉O的直径,且CF⊥AB,∴=,∴=,∴CD=BF.在△BFG和△CDG中,∴△BFG≌△CDG(AAS).
(2)连接OF,设☉O的半径为r.在Rt△ADB中,BD2=AB2-AD2,即BD2=(2r)2-22,在Rt△OEF中,EF2=OF2-OE2,即EF2=r2-(r-2)2.∵==,∴=,∴BD=CF,∴BD2=CF2=(2EF)2=4EF2,即(2r)2-22=4[r2-(r-2)2],解得r=1(舍去)或r=3,∴BF2=EF2+BE2=32-(3-2)2+22=12,∴BF=2.
22.解:(1)如图,连接BC.由题意得△ABC为等边三角形,∴∠ABC=∠ACB=60°.∵∠ADC=∠ABC,∠ADB=∠ACB,∴∠ADB=∠ADC=60°.
(2)如图,在AD上取点E,F,使DE=DB,DF=DC,连接BE,CF.由(1)知∠ADB=∠ADC=60°,∴△BDE,△CDF均为等边三角形,∴∠DEB=∠DFC=60°,∴∠AEB=∠CFA=120°.又∵∠FAC+∠FCA=∠DFC=60°,∠FAC+∠EAB=∠BAC=60°,∴∠EAB=∠FCA.在△ABE和△CAF中,∴△ABE≌△CAF(AAS),∴AE=CF,∴AD=DE+AE=BD+CF=BD+CD.
23.解:(1)∵∠CAD=∠CBD,∠ACH=∠CBD,∴∠ACH=∠CAD,∴AD∥CH.又∵AD=CH,∴四边形ADCH是平行四边形.
(2)①∵AB是☉O的直径,∴∠ACB=∠ADB=90°.∵AD∥CH,∴∠DHC=90°.∵AC=BC, ∴△ABC为等腰直角三角形,∴∠BAC=45°,∴∠HDC=∠BAC=45°,∴∠DCH=45°,∴△DHC为等腰直角三角形.
②∵四边形ABCD是☉O的内接四边形,∴∠PDA=∠PBC.∵∠P=∠P,∴△PBC∽△PDA,∴=.∵AD=CH,PB=PD,∴==,∴BC=CH.∵△DHC为等腰直角三角形,∴CD=CH.∵△ABC为等腰直角三角形,∴AB=BC.∵AB+CD=2(+1),∴BC+CH=2(+1),即×(+1)CH=2(+1),解得CH=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学期中达标检测卷
【检测内容:第24章 圆】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.如图,AB,AC是圆的两条弦,AD是圆的一条直径,且AD平分∠BAC.下列结论不一定正确的是( )
A.= B.= C.BC⊥AD D.∠B=∠C
3.如图,四边形ABCD内接于☉O,E为BC延长线上的一个点.若∠A=n°,则∠DCE的度数为( )
A.(180-n)° B.n° C.(90-n)° D.(90+n)°
4.如图,在☉O中,=,∠BAC=50°,则∠AEC的度数为( )
A.65° B.75° C.50° D.55°
5.如图,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EF
A.(2,-1) B.(1,-2) C.(-2,1) D.(-2,-1)
7.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
A. B. C. D.
8.如图,☉O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65° B.60° C.58° D.50°
9.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于点D,则AD的长为( )
A.2 B.4 C.5 D.6
10.如图,在☉O中,AB是☉O的直径,AB=10,==,E是点D关于AB的对称点,M是AB上的一个动点,下列结论:①∠BOE=60°;②∠CED=∠DOB;③DM⊥CE;④ CM+DM的最小值是10.上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是 .
12.如图,☉O是△ABC的外接圆,BC=10,∠B=45°,tan C=,则☉O的半径是 .
13.在等腰直角△ABC中,∠C=90°,O为直角边上的一个点,以点O为圆心、OC长为半径作☉O,☉O与斜边AB相切于点D,连接CD,则∠ACD= .
14.如图,在△ABC中,∠ACB=90°,sin ∠A=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A'B'上的动点,以点P为圆心、PA'长为半径作☉P.
(1)当☉P与△ABC的边AC相切时,☉P的半径为 ;
(2)当☉P与△ABC的边AB相切时,☉P的周长为 .
三、(本大题共2小题,每小题8分,满分16分)
15.在平面直角坐标系中,有三点A(-1,-1),P(0,-1),Q(-2,0),若以点A为圆心、OA长为半径作圆,试判断点P,Q与☉A的位置关系.
16.如图,AB是☉O的直径,E为BC的中点,AB=4,∠BED=120°,求图中阴影部分的面积.
四、(本大题共2小题,每小题8分,满分16分)
17.如果从半径为5 cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.
18.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点的坐标分别为A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心顺时针旋转90°,得到△A1B1C,请画出△A1B1C;
(2)平移△A1B1C,使点A1的对应点A2的坐标为(2,0),请画出平移后对应的△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,△ABC内接于☉O,AB为☉O的直径,AB=10,AC=6,连接OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
20.如图,已知AB是☉O的直径,C是圆上一点(不与点A,B重合).
(1)用尺规过点C作AB的垂线,交☉O于点D;(保留作图痕迹,不写作法)
(2)若AC=4,BC=2,求(1)中所作的弦CD的长.
六、(本题满分12分)
21.如图,AB是☉O的直径,C为的中点,CF为☉O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
七、(本题满分12分)
22.如图,已知在圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
(1)求∠ADB与∠ADC的大小;
(2)求证:AD=BD+CD.
八、(本题满分14分)
23.如图,四边形ABCD是☉O的内接四边形,线段AB是☉O的直径,连接AC,BD.H是线段BD上的一点,连接AH,CH且∠ACH=∠CBD,AD=CH,BA的延长线与CD的延长线相交于点P.
(1)求证:四边形ADCH是平行四边形.
(2)若AC=BC,PB=PD,AB+CD=2(+1),
①求证:△DHC为等腰直角三角形;
②求CH的长度.
参 考 答 案
1.A 2.A 3.B 4.A 5.C 6. A 7.B 8.B 9.B 10.C
11.(2,1) 12. 13.67.5°或22.5° 提示:∵△ABC为等腰直角三角形,∴∠A=∠B=45°,∠ACB=90°.①如图,当点O在BC上时,∵☉O与斜边AB相切于点D,∴OD⊥AB,∴∠BOD=45°.由圆周角定理得∠BCD=∠BOD=22.5°,∴∠ACD=90°-22.5°=67.5°.②如图,当点O'在AC上时,∵☉O'与斜边AB相切于点D',∴O'D'⊥AB,∴∠AO'D'=45°.由圆周角定理得∠ACD'=∠AO'D'=22.5°.综上所述,∠ACD=67.5°或22.5°.
14.(1) (2)
15.解:∵点A(-1,-1),P(0,-1),Q(-2,0),∴OA==,AP=1,AQ==,即AP
17.解:∵从半径为5 cm的圆形纸片上剪去圆周的一个扇形,∴留下的扇形的弧长为=8π(cm).根据圆锥底面圆的周长等于扇形弧长,∴圆锥的底面半径r==4(cm),∴圆锥的高为=3(cm).
18.解:(1)如图所示,△A1B1C即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)如图所示,旋转中心的坐标为(-1,-1).
19.解:(1)∵AE=DE,OC是半径,∴=,∴∠CAD=∠CBA.
(2)∵AB是直径,∴∠ACB=90°.∵AE=DE,∴OC⊥AD,∴∠AEC=90°.∴∠AEC=∠ACB.由(1)知∠CAE=∠ABC,∴△AEC∽△BCA,∴=,即=,解得CE=3.6.∵OC=AB=5,∴OE=OC-EC=5-3.6=1.4.
20.解:(1)作图如图所示.
(2)∵AB是☉O的直径,∴∠ACB=90°,∴AB===2.∵S△ABC=AC·BC=AB·CE,∴CE==,∴CD=2CE=.
21.解:(1)∵C为的中点,∴=.∵AB是☉O的直径,且CF⊥AB,∴=,∴=,∴CD=BF.在△BFG和△CDG中,∴△BFG≌△CDG(AAS).
(2)连接OF,设☉O的半径为r.在Rt△ADB中,BD2=AB2-AD2,即BD2=(2r)2-22,在Rt△OEF中,EF2=OF2-OE2,即EF2=r2-(r-2)2.∵==,∴=,∴BD=CF,∴BD2=CF2=(2EF)2=4EF2,即(2r)2-22=4[r2-(r-2)2],解得r=1(舍去)或r=3,∴BF2=EF2+BE2=32-(3-2)2+22=12,∴BF=2.
22.解:(1)如图,连接BC.由题意得△ABC为等边三角形,∴∠ABC=∠ACB=60°.∵∠ADC=∠ABC,∠ADB=∠ACB,∴∠ADB=∠ADC=60°.
(2)如图,在AD上取点E,F,使DE=DB,DF=DC,连接BE,CF.由(1)知∠ADB=∠ADC=60°,∴△BDE,△CDF均为等边三角形,∴∠DEB=∠DFC=60°,∴∠AEB=∠CFA=120°.又∵∠FAC+∠FCA=∠DFC=60°,∠FAC+∠EAB=∠BAC=60°,∴∠EAB=∠FCA.在△ABE和△CAF中,∴△ABE≌△CAF(AAS),∴AE=CF,∴AD=DE+AE=BD+CF=BD+CD.
23.解:(1)∵∠CAD=∠CBD,∠ACH=∠CBD,∴∠ACH=∠CAD,∴AD∥CH.又∵AD=CH,∴四边形ADCH是平行四边形.
(2)①∵AB是☉O的直径,∴∠ACB=∠ADB=90°.∵AD∥CH,∴∠DHC=90°.∵AC=BC, ∴△ABC为等腰直角三角形,∴∠BAC=45°,∴∠HDC=∠BAC=45°,∴∠DCH=45°,∴△DHC为等腰直角三角形.
②∵四边形ABCD是☉O的内接四边形,∴∠PDA=∠PBC.∵∠P=∠P,∴△PBC∽△PDA,∴=.∵AD=CH,PB=PD,∴==,∴BC=CH.∵△DHC为等腰直角三角形,∴CD=CH.∵△ABC为等腰直角三角形,∴AB=BC.∵AB+CD=2(+1),∴BC+CH=2(+1),即×(+1)CH=2(+1),解得CH=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
