第九章 概率初步 3 等可能事件的概率 第3课时 与面积相关的概率(含答案)
文档属性
| 名称 | 第九章 概率初步 3 等可能事件的概率 第3课时 与面积相关的概率(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 08:09:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 概率初步
3 等可能事件的概率
第3课时 与面积相关的概率
知识梳理
一般地,在一次试验中,结果落在区域D中每一点都是等可能的,用A表示“试验结果落在D中的一个小区域M中”这个事件,那么事件A发生的概率为P(A)=__________.
基础练习
1.地球上陆地与海洋面积的比是3∶7,宇宙中一块陨石进入地球,落在陆地上的概率是( )
2.如图,在等边三角形ABC中,D,E,F分别是边AB,BC,AC的中点.若用小针进行投针试验,则命中涂色区域的概率为( )
3.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在涂色区域的概率是____.
4.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”可见卖油翁的技艺之高超.若铜钱直径为4cm,中间有边长为1cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入小孔中的概率是____.
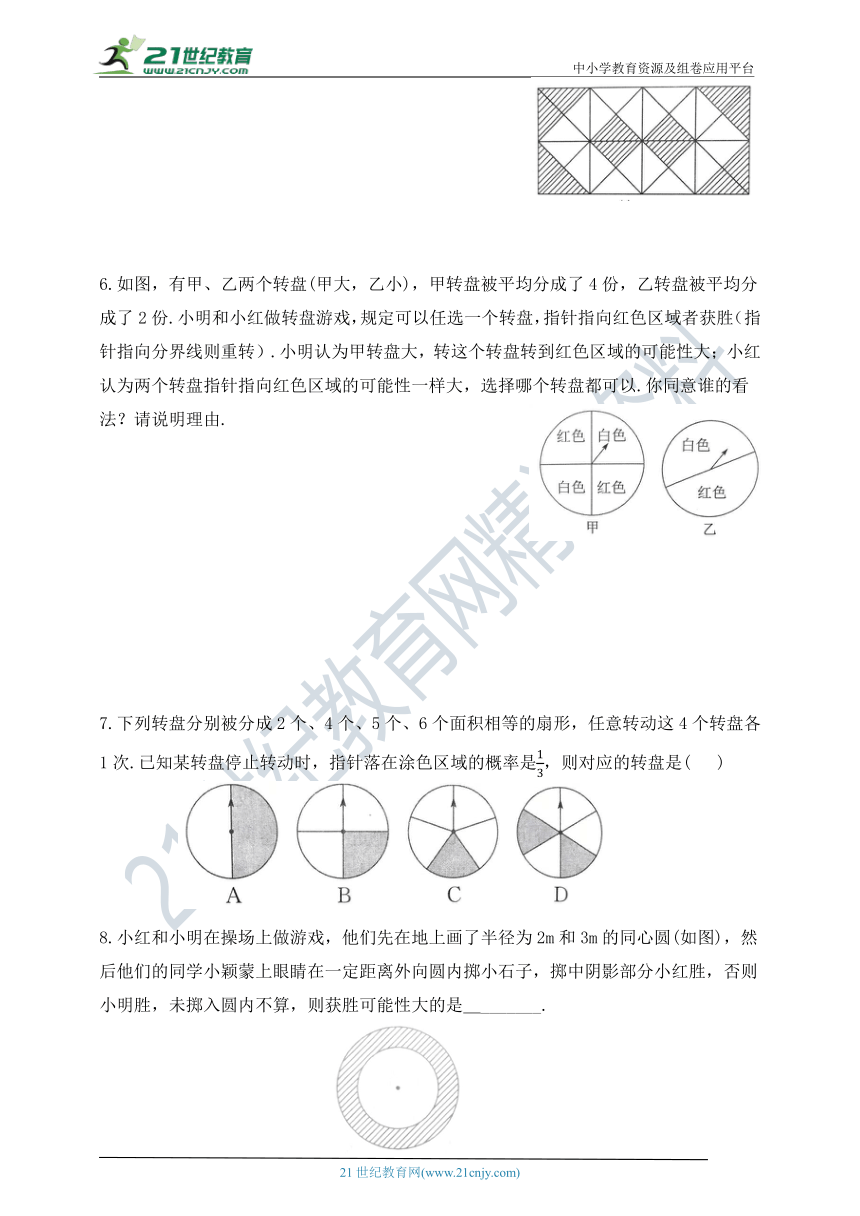
5.如图,往图中的长方形区域掷石子.若石子落在阴影部分上,则甲获胜;若石子落在空白部分上,则乙获胜(石子每次均落在长方形区域).你认为谁获胜的概率较大?
6.如图,有甲、乙两个转盘(甲大,乙小),甲转盘被平均分成了4份,乙转盘被平均分成了2份.小明和小红做转盘游戏,规定可以任选一个转盘,指针指向红色区域者获胜(指针指向分界线则重转).小明认为甲转盘大,转这个转盘转到红色区域的可能性大;小红认为两个转盘指针指向红色区域的可能性一样大,选择哪个转盘都可以.你同意谁的看法?请说明理由.
7.下列转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在涂色区域的概率是,则对应的转盘是( )
8.小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),然后他们的同学小颖蒙上眼睛在一定距离外向圆内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圆内不算,则获胜可能性大的是________.
9.二十四节气被列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是___.
10.如图,正方形ABCD的边长为2,正方形ABCD内的图形来自中国古代的太极图.现随机向正方形内掷一枚小针,则针尖落在涂色区域内的概率为______.
11.向如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个小正三角形内(边线忽略不计).
(1)投针一次,针落在图中涂色区域的概率是:多少?
(2)要使针落在图中涂色区域和空白区域的概率均为,则还要给几个小正三角形涂色 请在图中画出.
12.如图,小红家阳台的地面铺设着18块灰、白两种颜色的面积相等的方砖,她从房间向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)分别求小皮球停留在灰色方砖与白色方砖上的概率.
(2)上面哪个概率较大 要使这两种情况的概率相等,并且使颜色有规律,应改变第几行第几列的方砖颜色?怎样改变?
参考答案
[知识梳理]
[课堂作业]
1.B 2.C
5.甲获胜的概率为 乙获胜的概率为 ∵∴乙获胜的概率较大
6.同意小红的看法 理由:∵P(甲转盘指针指向红色区域 P(乙转盘指针指向红色区域),∴两个转盘指针指向红色区域的可能性一样大.∴同意小红的看法.
[巩固提高]
7.D 8.小红 9.
11.(1)∵涂色区域的面积与三角形的面积的比值是 ,∴投针一次,针落在图中涂色区域的概率为 .
(2)要使针落在图中涂色区域和空白区域的概率均为,则还要给2个小正三角形涂色(图略).
12.(1)由题图,得共有18块方砖,其中白色方砖有8块,灰色方砖有10块,∴小皮球停留在灰色方砖上的概率是 小皮球停留在白色方砖上的概率是 . ∴小皮球停留在灰色方砖上的概率较大.要使这两种情况的概率相等,并且使颜色有规律,应改变第2行从左往右数第4列的方砖颜色,灰色方砖改变为白色方砖.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 概率初步
3 等可能事件的概率
第3课时 与面积相关的概率
知识梳理
一般地,在一次试验中,结果落在区域D中每一点都是等可能的,用A表示“试验结果落在D中的一个小区域M中”这个事件,那么事件A发生的概率为P(A)=__________.
基础练习
1.地球上陆地与海洋面积的比是3∶7,宇宙中一块陨石进入地球,落在陆地上的概率是( )
2.如图,在等边三角形ABC中,D,E,F分别是边AB,BC,AC的中点.若用小针进行投针试验,则命中涂色区域的概率为( )
3.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在涂色区域的概率是____.
4.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”可见卖油翁的技艺之高超.若铜钱直径为4cm,中间有边长为1cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入小孔中的概率是____.
5.如图,往图中的长方形区域掷石子.若石子落在阴影部分上,则甲获胜;若石子落在空白部分上,则乙获胜(石子每次均落在长方形区域).你认为谁获胜的概率较大?
6.如图,有甲、乙两个转盘(甲大,乙小),甲转盘被平均分成了4份,乙转盘被平均分成了2份.小明和小红做转盘游戏,规定可以任选一个转盘,指针指向红色区域者获胜(指针指向分界线则重转).小明认为甲转盘大,转这个转盘转到红色区域的可能性大;小红认为两个转盘指针指向红色区域的可能性一样大,选择哪个转盘都可以.你同意谁的看法?请说明理由.
7.下列转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在涂色区域的概率是,则对应的转盘是( )
8.小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),然后他们的同学小颖蒙上眼睛在一定距离外向圆内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圆内不算,则获胜可能性大的是________.
9.二十四节气被列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是___.
10.如图,正方形ABCD的边长为2,正方形ABCD内的图形来自中国古代的太极图.现随机向正方形内掷一枚小针,则针尖落在涂色区域内的概率为______.
11.向如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个小正三角形内(边线忽略不计).
(1)投针一次,针落在图中涂色区域的概率是:多少?
(2)要使针落在图中涂色区域和空白区域的概率均为,则还要给几个小正三角形涂色 请在图中画出.
12.如图,小红家阳台的地面铺设着18块灰、白两种颜色的面积相等的方砖,她从房间向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)分别求小皮球停留在灰色方砖与白色方砖上的概率.
(2)上面哪个概率较大 要使这两种情况的概率相等,并且使颜色有规律,应改变第几行第几列的方砖颜色?怎样改变?
参考答案
[知识梳理]
[课堂作业]
1.B 2.C
5.甲获胜的概率为 乙获胜的概率为 ∵∴乙获胜的概率较大
6.同意小红的看法 理由:∵P(甲转盘指针指向红色区域 P(乙转盘指针指向红色区域),∴两个转盘指针指向红色区域的可能性一样大.∴同意小红的看法.
[巩固提高]
7.D 8.小红 9.
11.(1)∵涂色区域的面积与三角形的面积的比值是 ,∴投针一次,针落在图中涂色区域的概率为 .
(2)要使针落在图中涂色区域和空白区域的概率均为,则还要给2个小正三角形涂色(图略).
12.(1)由题图,得共有18块方砖,其中白色方砖有8块,灰色方砖有10块,∴小皮球停留在灰色方砖上的概率是 小皮球停留在白色方砖上的概率是 . ∴小皮球停留在灰色方砖上的概率较大.要使这两种情况的概率相等,并且使颜色有规律,应改变第2行从左往右数第4列的方砖颜色,灰色方砖改变为白色方砖.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
