沪科版九年级下册数学阶段达标检测卷—第25章 投影与视图(含答案)
文档属性
| 名称 | 沪科版九年级下册数学阶段达标检测卷—第25章 投影与视图(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 08:18:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学达标检测卷
【检测内容:第25章 投影与视图】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.一块圆形铁片,它的正投影是( )
A.圆 B.椭圆 C.线段 D.以上结果都有可能
2.木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
3.下列属于中心投影现象的是( )
A.早上升旗时地面上旗杆的影子 B.上午人走在路上的影子
C.中午用来乘凉的树影 D.晚上人走在路灯下的影子
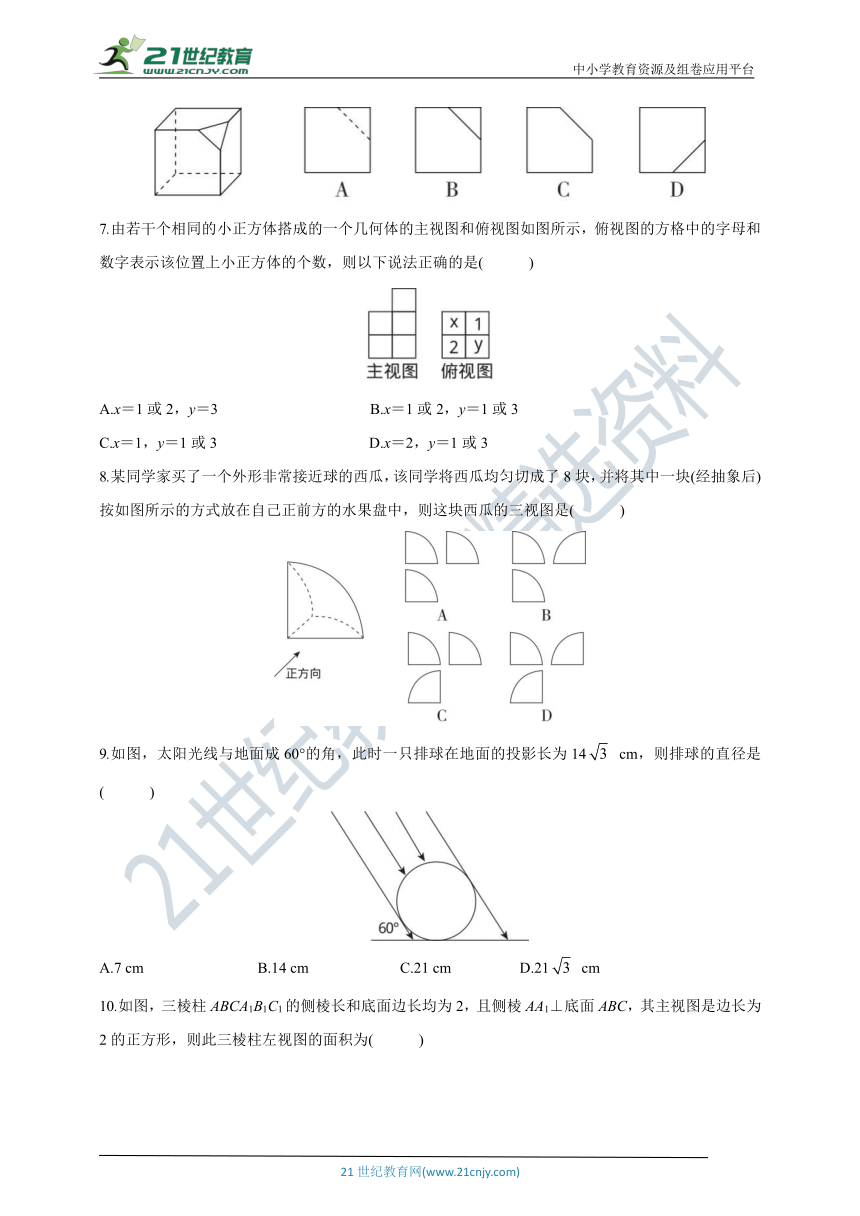
4.如图,该几何体的俯视图是( )
5.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
6.如图所示的几何体的主视图是( )
7.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
8.某同学家买了一个外形非常接近球的西瓜,该同学将西瓜均匀切成了8块,并将其中一块(经抽象后)按如图所示的方式放在自己正前方的水果盘中,则这块西瓜的三视图是( )
9.如图,太阳光线与地面成60°的角,此时一只排球在地面的投影长为14 cm,则排球的直径是( )
A.7 cm B.14 cm C.21 cm D.21 cm
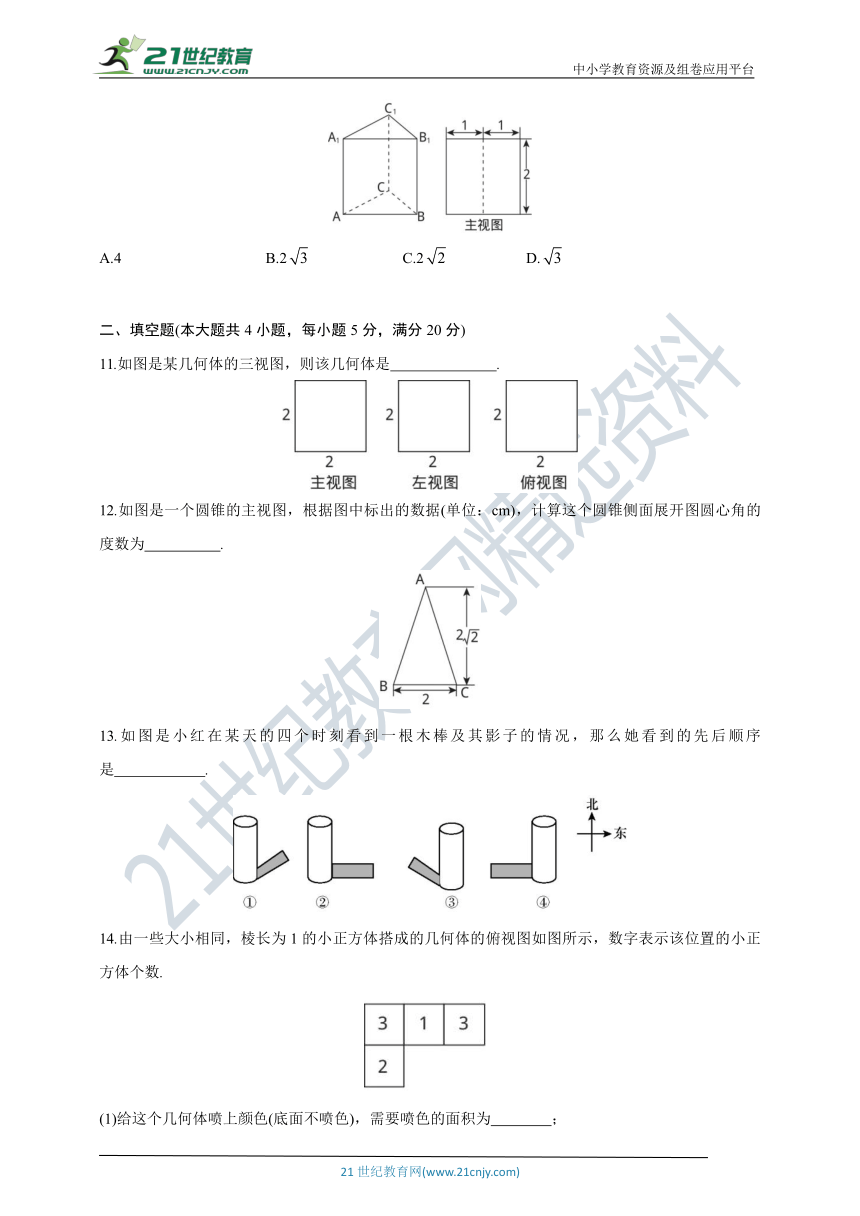
10.如图,三棱柱ABCA1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
A.4 B.2 C.2 D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图是某几何体的三视图,则该几何体是 .
12.如图是一个圆锥的主视图,根据图中标出的数据(单位:cm),计算这个圆锥侧面展开图圆心角的度数为 .
13.如图是小红在某天的四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 .
14.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的小正方体个数.
(1)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为 ;
(2)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
三、(本大题共2小题,每小题8分,满分16分)
15.小华和小明在同一盏路灯下的影长如图所示,请找出路灯灯泡的位置.
16.如图,把一面镜子(镜子的厚度忽略不计)放在离树底B点8.4米的点E处,再沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米.已知观察者目高CD=1.6米,求树AB的高度约为多少米.(精确到0.1米)
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在Rt△ABC中,∠ACB=90°,在阳光的垂直照射下,点C的投影为斜边AB上的点D.
(1)试探究线段AC,AB和AD之间的数量关系,并说明理由.
(2)线段BC,AB和BD之间也有类似(1)中的关系吗 请说明理由.
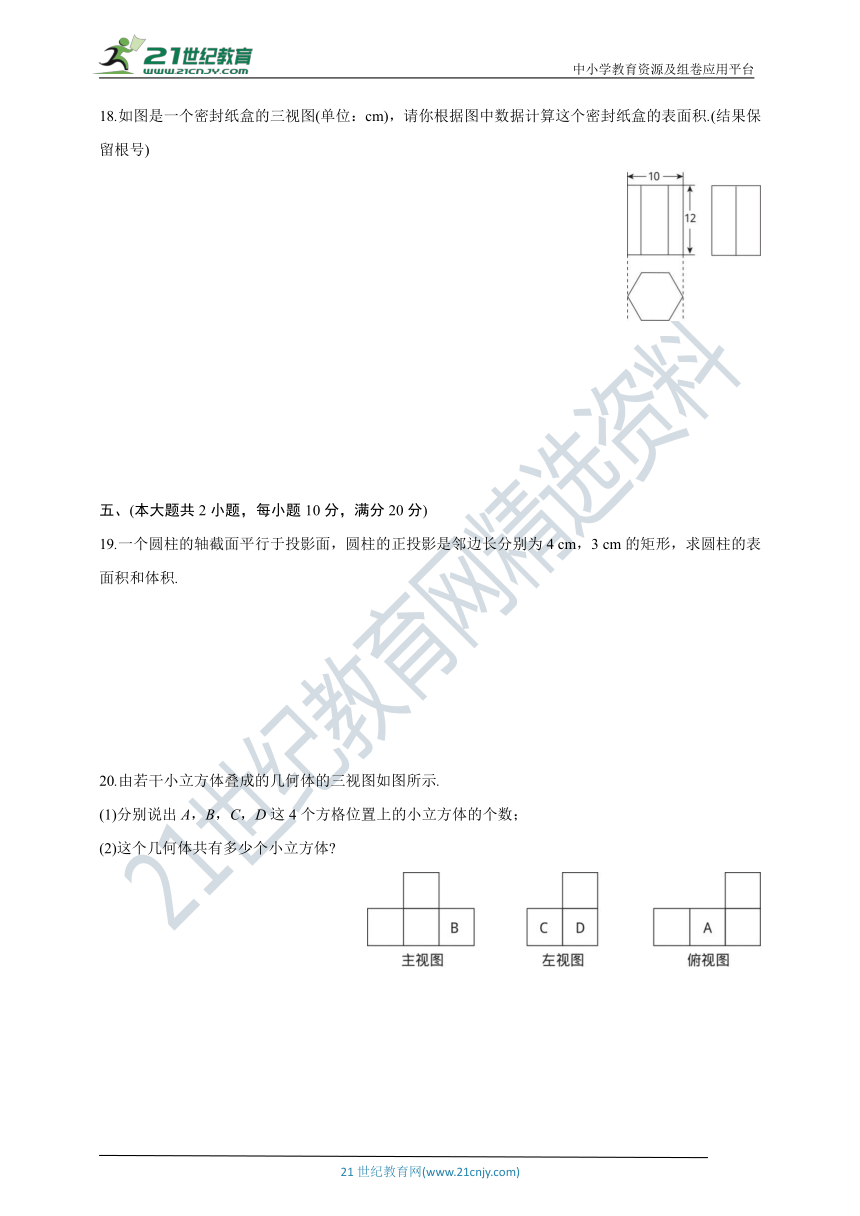
18.如图是一个密封纸盒的三视图(单位:cm),请你根据图中数据计算这个密封纸盒的表面积.(结果保留根号)
五、(本大题共2小题,每小题10分,满分20分)
19.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,求圆柱的表面积和体积.
20.由若干小立方体叠成的几何体的三视图如图所示.
(1)分别说出A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体共有多少个小立方体
六、(本题满分12分)
21.在一个阳光明媚的上午,王老师组织学生测量小山坡上的一棵大树CD的高度.他们测得山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7 m的小明(AB)在地面上的影长BP为1.2 m,此刻大树CD在斜坡上的影长DQ为5 m,求大树的高度.
七、(本题满分12分)
22.如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.(参考数据:≈1.732)
(1)求楼房的高度约为多少米 (结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳 请说明理由.
八、(本题满分14分)
23.如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2米,且恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方(已知王琳身高1.8米,路灯B高9米).
(1)标出王琳站在P处在路灯B下的影子;
(2)计算王琳站在Q处在路灯A下的影长;
(3)计算路灯A的高度.
参 考 答 案
1.D 2.D 3.D 4.A 5.A 6.B 7.A 8.B 9.C 10.B
11.正方体 12.120° 13.④③①② 14.(1)32 (2)1
15.解:如图,点P即为路灯灯泡所在的位置.
16.解:∵∠CED=∠AEB,CD⊥DB,AB⊥BD,∴△CED∽△AEB,∴=.∵CD=1.6米,DE=2.4米,BE=8.4米,∴=,解得AB==5.6(米).答:树AB的高度约为5.6米.
17.解:(1)AC2=AD·AB.理由:∵CD⊥AB,∴∠ADC=∠ACB=90°,且∠A=∠A,∴△ADC∽△ACB,∴=,即AC2=AD·AB.
(2)BC2=AB·BD.理由略.
18.解:根据该密封纸盒的三视图可知,它是一个正六棱柱,且高为12 cm,底面边长为5 cm,∴侧面积为6×5×12=360(cm2),密封纸盒的上、下底面的面积和为×5××5×12=75(cm2),∴这个密封纸盒的表面积为(75+360) cm2.
19.解:由题可知,有两种情况:①当圆柱底面圆的半径为 cm,高为4 cm时,圆柱的表面积为2π××4+2π×()2=12π+π=π(cm2),体积为π()2×4=9π(cm3);②当圆柱底面圆的半径为2 cm,高为3 cm时,圆柱的表面积为2π×2×3+2π×22=12π+8π=20π(cm2),体积为π×22×3=12π(cm3).
20.解:(1)观察三个视图,可知A位置上有2个小立方体,B位置上有2个小立方体,C位置上有1个小立方体,D位置上有3个小立方体.
(2)结合(1)中的分析,该几何体共有两层,上层有1个小立方体,下层有4个小立方体,共有5个小立方体.
21.解:过点Q作QE⊥DC于点E.根据题意,得△ABP∽△CEQ,则=,即=.由已知得EQ∥NO,则∠MON=∠DQE=30°.因为QD=5 m,所以DE= m,EQ= m,所以==,解得CE= m,故CD=CE+DE=+=(m).答:大树的高度为 m.
22.解:(1)当α=60°时,在Rt△ABE中,tan 60°=,∴AB=10·tan 60°=10≈10×1.732≈17.3(米).答:楼房的高度约为17.3米.
(2)当α=45°时,小猫还能晒到太阳.理由:假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为F,与MC的交点为H.∵∠BFA=45°,∴此时的影长AF=AB=17.3米,∴CF=AF-AC=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫还能晒到太阳.
23.解:(1)线段CP为王琳在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,∴=,即=,解得QD=1.5米.答:王琳站在Q处在路灯A下的影长为1.5米.
(3)∵Rt△DFQ∽Rt△DAC,∴=,∴=,解得AC=12米.答:路灯A的高度为12米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学达标检测卷
【检测内容:第25章 投影与视图】
本试卷共八大题,共23小题,满分150分,考试时间120分钟.
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.一块圆形铁片,它的正投影是( )
A.圆 B.椭圆 C.线段 D.以上结果都有可能
2.木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
3.下列属于中心投影现象的是( )
A.早上升旗时地面上旗杆的影子 B.上午人走在路上的影子
C.中午用来乘凉的树影 D.晚上人走在路灯下的影子
4.如图,该几何体的俯视图是( )
5.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
6.如图所示的几何体的主视图是( )
7.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
8.某同学家买了一个外形非常接近球的西瓜,该同学将西瓜均匀切成了8块,并将其中一块(经抽象后)按如图所示的方式放在自己正前方的水果盘中,则这块西瓜的三视图是( )
9.如图,太阳光线与地面成60°的角,此时一只排球在地面的投影长为14 cm,则排球的直径是( )
A.7 cm B.14 cm C.21 cm D.21 cm
10.如图,三棱柱ABCA1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
A.4 B.2 C.2 D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图是某几何体的三视图,则该几何体是 .
12.如图是一个圆锥的主视图,根据图中标出的数据(单位:cm),计算这个圆锥侧面展开图圆心角的度数为 .
13.如图是小红在某天的四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 .
14.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的小正方体个数.
(1)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为 ;
(2)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
三、(本大题共2小题,每小题8分,满分16分)
15.小华和小明在同一盏路灯下的影长如图所示,请找出路灯灯泡的位置.
16.如图,把一面镜子(镜子的厚度忽略不计)放在离树底B点8.4米的点E处,再沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米.已知观察者目高CD=1.6米,求树AB的高度约为多少米.(精确到0.1米)
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在Rt△ABC中,∠ACB=90°,在阳光的垂直照射下,点C的投影为斜边AB上的点D.
(1)试探究线段AC,AB和AD之间的数量关系,并说明理由.
(2)线段BC,AB和BD之间也有类似(1)中的关系吗 请说明理由.
18.如图是一个密封纸盒的三视图(单位:cm),请你根据图中数据计算这个密封纸盒的表面积.(结果保留根号)
五、(本大题共2小题,每小题10分,满分20分)
19.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,求圆柱的表面积和体积.
20.由若干小立方体叠成的几何体的三视图如图所示.
(1)分别说出A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体共有多少个小立方体
六、(本题满分12分)
21.在一个阳光明媚的上午,王老师组织学生测量小山坡上的一棵大树CD的高度.他们测得山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7 m的小明(AB)在地面上的影长BP为1.2 m,此刻大树CD在斜坡上的影长DQ为5 m,求大树的高度.
七、(本题满分12分)
22.如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.(参考数据:≈1.732)
(1)求楼房的高度约为多少米 (结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳 请说明理由.
八、(本题满分14分)
23.如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2米,且恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方(已知王琳身高1.8米,路灯B高9米).
(1)标出王琳站在P处在路灯B下的影子;
(2)计算王琳站在Q处在路灯A下的影长;
(3)计算路灯A的高度.
参 考 答 案
1.D 2.D 3.D 4.A 5.A 6.B 7.A 8.B 9.C 10.B
11.正方体 12.120° 13.④③①② 14.(1)32 (2)1
15.解:如图,点P即为路灯灯泡所在的位置.
16.解:∵∠CED=∠AEB,CD⊥DB,AB⊥BD,∴△CED∽△AEB,∴=.∵CD=1.6米,DE=2.4米,BE=8.4米,∴=,解得AB==5.6(米).答:树AB的高度约为5.6米.
17.解:(1)AC2=AD·AB.理由:∵CD⊥AB,∴∠ADC=∠ACB=90°,且∠A=∠A,∴△ADC∽△ACB,∴=,即AC2=AD·AB.
(2)BC2=AB·BD.理由略.
18.解:根据该密封纸盒的三视图可知,它是一个正六棱柱,且高为12 cm,底面边长为5 cm,∴侧面积为6×5×12=360(cm2),密封纸盒的上、下底面的面积和为×5××5×12=75(cm2),∴这个密封纸盒的表面积为(75+360) cm2.
19.解:由题可知,有两种情况:①当圆柱底面圆的半径为 cm,高为4 cm时,圆柱的表面积为2π××4+2π×()2=12π+π=π(cm2),体积为π()2×4=9π(cm3);②当圆柱底面圆的半径为2 cm,高为3 cm时,圆柱的表面积为2π×2×3+2π×22=12π+8π=20π(cm2),体积为π×22×3=12π(cm3).
20.解:(1)观察三个视图,可知A位置上有2个小立方体,B位置上有2个小立方体,C位置上有1个小立方体,D位置上有3个小立方体.
(2)结合(1)中的分析,该几何体共有两层,上层有1个小立方体,下层有4个小立方体,共有5个小立方体.
21.解:过点Q作QE⊥DC于点E.根据题意,得△ABP∽△CEQ,则=,即=.由已知得EQ∥NO,则∠MON=∠DQE=30°.因为QD=5 m,所以DE= m,EQ= m,所以==,解得CE= m,故CD=CE+DE=+=(m).答:大树的高度为 m.
22.解:(1)当α=60°时,在Rt△ABE中,tan 60°=,∴AB=10·tan 60°=10≈10×1.732≈17.3(米).答:楼房的高度约为17.3米.
(2)当α=45°时,小猫还能晒到太阳.理由:假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为F,与MC的交点为H.∵∠BFA=45°,∴此时的影长AF=AB=17.3米,∴CF=AF-AC=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫还能晒到太阳.
23.解:(1)线段CP为王琳在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,∴=,即=,解得QD=1.5米.答:王琳站在Q处在路灯A下的影长为1.5米.
(3)∵Rt△DFQ∽Rt△DAC,∴=,∴=,解得AC=12米.答:路灯A的高度为12米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
