6.3 实数(第1课时) 课件(共37张PPT)
文档属性
| 名称 | 6.3 实数(第1课时) 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 07:51:32 | ||
图片预览








文档简介
(共37张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第六章 实数
6.3 实数
第1课时 实数
1.了解实数的意义,并能将实数按要求进行准确的分类.
2.熟练掌握实数大小的比较方法.
3.了解实数和数轴上的点一一对应,能用数轴上的点表示无理数.
学习目标
(1)请把下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
新知一 实数的概念和分类
合作探究
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…(两个1之间依次多1个0),
-168.3232232223…(两个3之间依次多1个2).
=1.41421356237309504880168…
=1.70997594667669698935310…
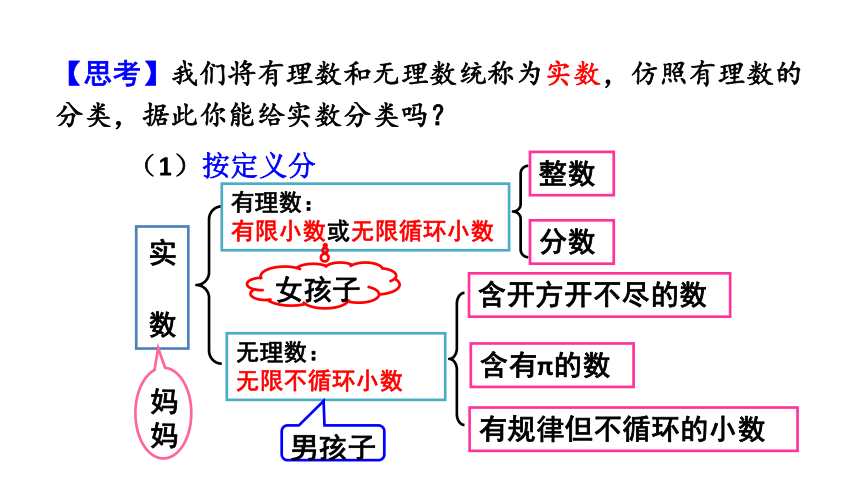
【思考】我们将有理数和无理数统称为实数,仿照有理数的分类,据此你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
女孩子
男孩子
妈妈
含开方开不尽的数
有规律但不循环的小数
含有π的数
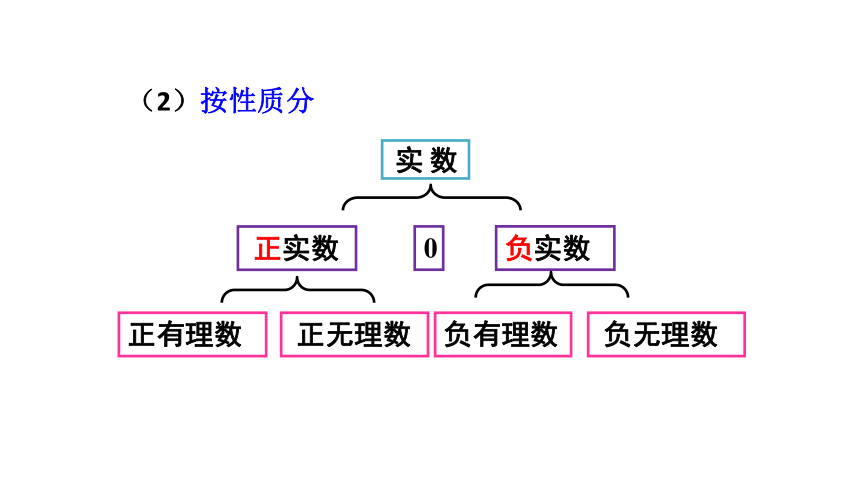
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
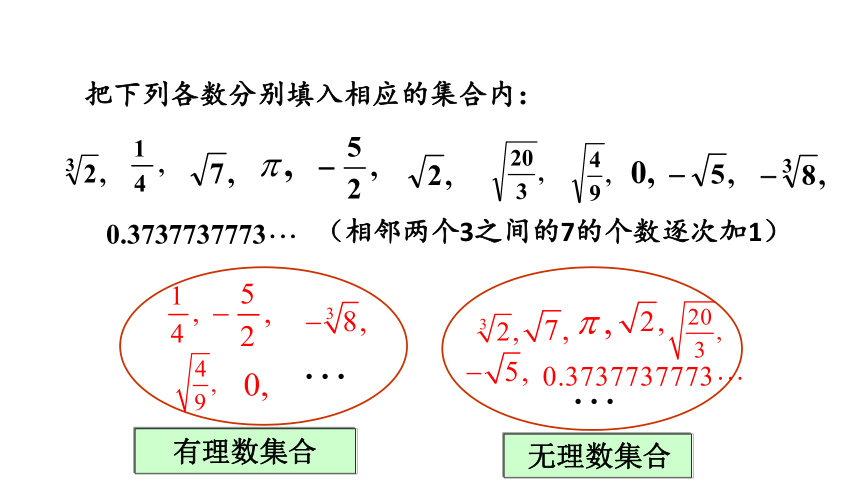
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
把下列各数分别填入相应的集合内:
无理数:
有理数:
负实数:
正实数:
例 将下列各数分别填入下列相应的括号内:
典例精析 实数的分类
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
巩固新知
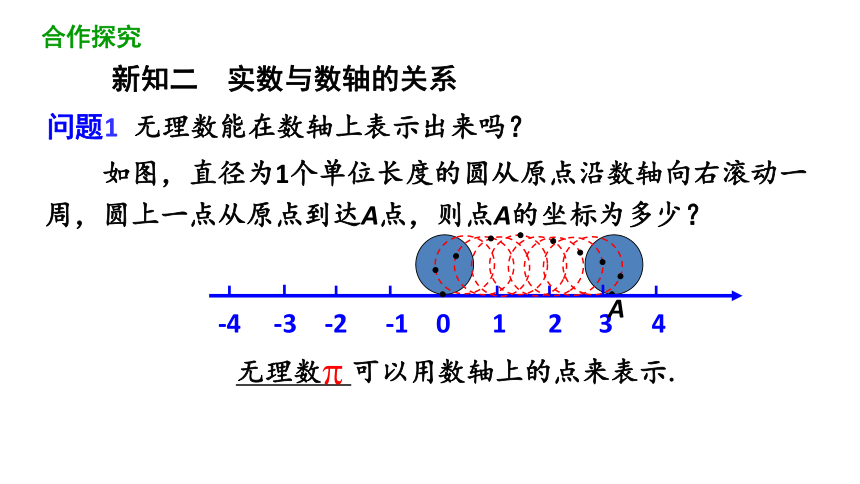
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题1 无理数能在数轴上表示出来吗?
新知二 实数与数轴的关系
合作探究
-2
-1
0
1
2
-
问题2(1)你能在数轴上表示出 吗?
(2)如果将所有有理数都标到数轴上,那么数轴能填满吗?
-2
-1
0
1
2
B
A
C
在数轴上表示的两个实数,右边的数总比左边的数大.
数轴上的点有些
表示有理数,有
些表示无理数.
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数.即实数和数轴上的点是一一对应的.
例 如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点C到点A的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2-
典例精析 求数轴上的点表示的实数值
A
B
-1
0
与有理数一样,实数也可以比较大小:
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
正数大于零,负数小于零,正数大于负数.
与有理数一样,在实数范围内:
新知三 实数大小的比较
合作探究
,2可以分别看作是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
例 在数轴上表示下列各点,比较它们的大小, 并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
典例精析 比较实数的大小
解:
-2< < 1< <
试在数轴上标出π, , 的大致位置,并借助数轴比较它们的大小.
解析:因为π≈3.14, ≈-2.24, ≈1.73,所以可以近似地标出它们在数轴上的位置,如图(其中点A表示π,点B表示 ,点C表示 ).
因为数轴上右边的点表示的数总大于左边的点表示的数,所以可知 < <π.
巩固新知
D
D
课堂练习
B
5.(4分)下列说法:
①实数包括有理数、无理数和0;②有理数和无理数都是实数;
③正实数和负实数统称为实数;④实数既是有理数又是无理数.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
A
3
-6,-|-3|,0,…
8.(5分)和数轴上的点成一一对应关系的数是( )
A.自然数 B.有理数
C.无理数 D.实数
D
9.(4分)如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周
(不滑动),圆上的一点由原点到达点O′,
点O′所对应的数值是____.
π
实数的概念、分类、与数轴的关系
无理数的概念
实数的概念
实数的分类
实数与数轴的关系
实数的大小比较
有理数和无理数统称为实数
与数轴上的点一一对应
无限不循环小数
归纳新知
B
课后练习
B
D
2
4
解:由题意得,无理数有2个,所以x=2;
整数有0个,所以y=0;非负数有4个,所以z=4,
所以x+y+z=2+0+4=6
10.先阅读然后解答提出的问题:
设a,b是有理数,且满足a+b=3-2,求b3的值.
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第六章 实数
6.3 实数
第1课时 实数
1.了解实数的意义,并能将实数按要求进行准确的分类.
2.熟练掌握实数大小的比较方法.
3.了解实数和数轴上的点一一对应,能用数轴上的点表示无理数.
学习目标
(1)请把下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
新知一 实数的概念和分类
合作探究
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…(两个1之间依次多1个0),
-168.3232232223…(两个3之间依次多1个2).
=1.41421356237309504880168…
=1.70997594667669698935310…
【思考】我们将有理数和无理数统称为实数,仿照有理数的分类,据此你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
女孩子
男孩子
妈妈
含开方开不尽的数
有规律但不循环的小数
含有π的数
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
把下列各数分别填入相应的集合内:
无理数:
有理数:
负实数:
正实数:
例 将下列各数分别填入下列相应的括号内:
典例精析 实数的分类
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
巩固新知
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题1 无理数能在数轴上表示出来吗?
新知二 实数与数轴的关系
合作探究
-2
-1
0
1
2
-
问题2(1)你能在数轴上表示出 吗?
(2)如果将所有有理数都标到数轴上,那么数轴能填满吗?
-2
-1
0
1
2
B
A
C
在数轴上表示的两个实数,右边的数总比左边的数大.
数轴上的点有些
表示有理数,有
些表示无理数.
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数.即实数和数轴上的点是一一对应的.
例 如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点C到点A的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2-
典例精析 求数轴上的点表示的实数值
A
B
-1
0
与有理数一样,实数也可以比较大小:
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
正数大于零,负数小于零,正数大于负数.
与有理数一样,在实数范围内:
新知三 实数大小的比较
合作探究
,2可以分别看作是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
例 在数轴上表示下列各点,比较它们的大小, 并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
典例精析 比较实数的大小
解:
-2< < 1< <
试在数轴上标出π, , 的大致位置,并借助数轴比较它们的大小.
解析:因为π≈3.14, ≈-2.24, ≈1.73,所以可以近似地标出它们在数轴上的位置,如图(其中点A表示π,点B表示 ,点C表示 ).
因为数轴上右边的点表示的数总大于左边的点表示的数,所以可知 < <π.
巩固新知
D
D
课堂练习
B
5.(4分)下列说法:
①实数包括有理数、无理数和0;②有理数和无理数都是实数;
③正实数和负实数统称为实数;④实数既是有理数又是无理数.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
A
3
-6,-|-3|,0,…
8.(5分)和数轴上的点成一一对应关系的数是( )
A.自然数 B.有理数
C.无理数 D.实数
D
9.(4分)如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周
(不滑动),圆上的一点由原点到达点O′,
点O′所对应的数值是____.
π
实数的概念、分类、与数轴的关系
无理数的概念
实数的概念
实数的分类
实数与数轴的关系
实数的大小比较
有理数和无理数统称为实数
与数轴上的点一一对应
无限不循环小数
归纳新知
B
课后练习
B
D
2
4
解:由题意得,无理数有2个,所以x=2;
整数有0个,所以y=0;非负数有4个,所以z=4,
所以x+y+z=2+0+4=6
10.先阅读然后解答提出的问题:
设a,b是有理数,且满足a+b=3-2,求b3的值.
https://www.21cnjy.com/help/help_extract.php
