北师大版七年级下册数学4.3 探索三角形全等的条件 课件(共81张PPT)
文档属性
| 名称 | 北师大版七年级下册数学4.3 探索三角形全等的条件 课件(共81张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 07:03:19 | ||
图片预览




文档简介
(共81张PPT)
北师大版 初中数学
探索三角形全等的条件
利用“边边边”判定三角形全等
北师大版 初中数学
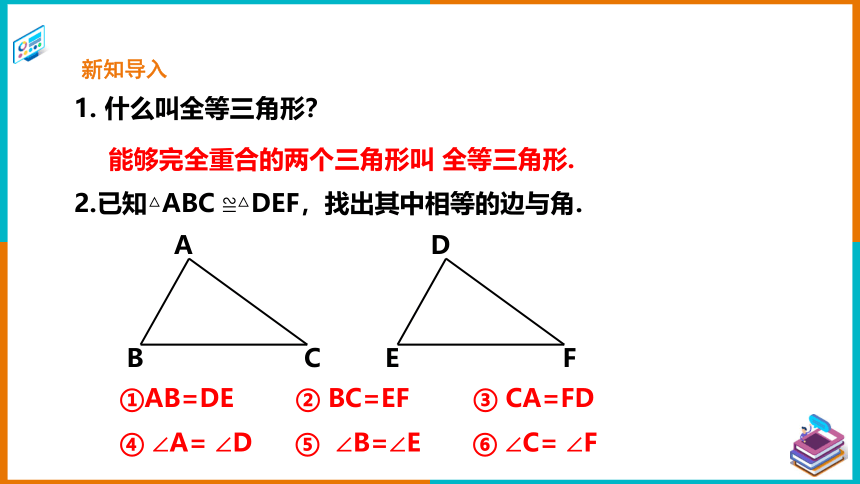
新知导入
1. 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
A
B
C
D
E
F
2.已知△ABC ≌△DEF,找出其中相等的边与角.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
新知讲解
【思考】
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?……
新知讲解
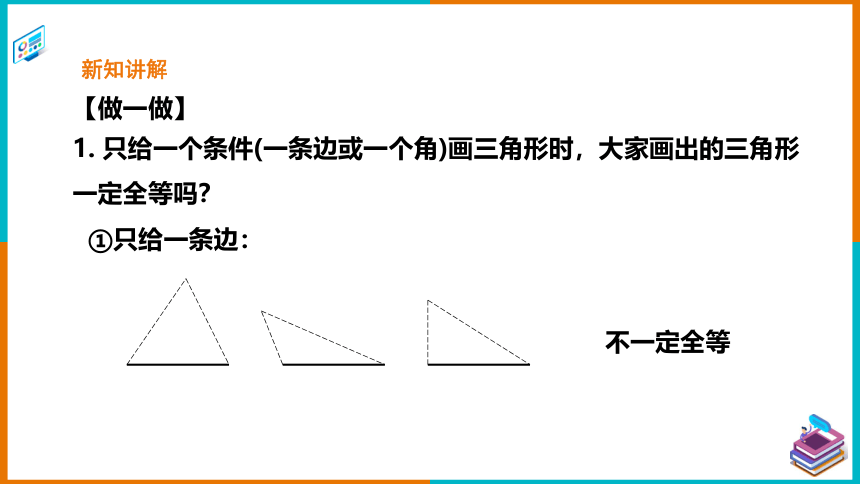
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
①只给一条边:
不一定全等
新知讲解
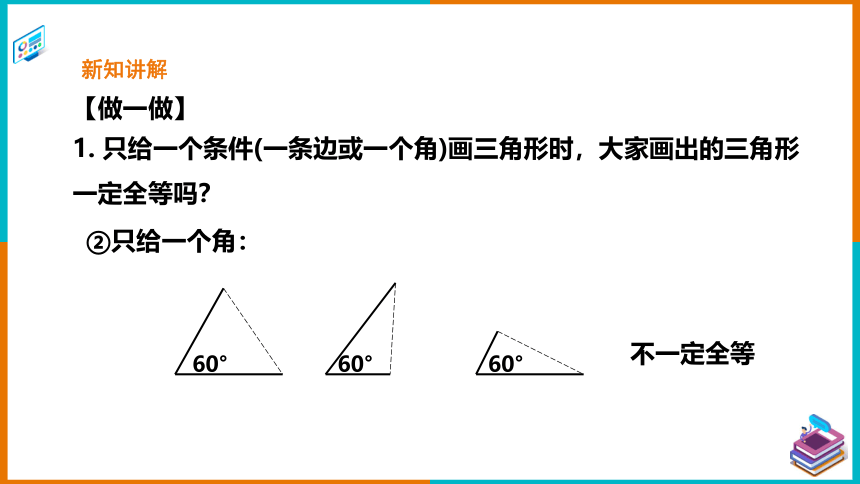
②只给一个角:
60°
60°
60°
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
新知讲解
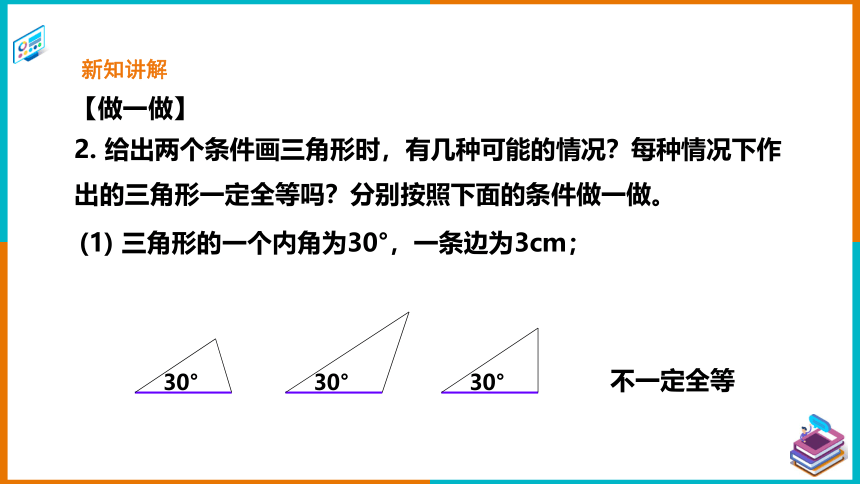
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(1) 三角形的一个内角为30°,一条边为3cm;
30°
30°
30°
不一定全等
新知讲解
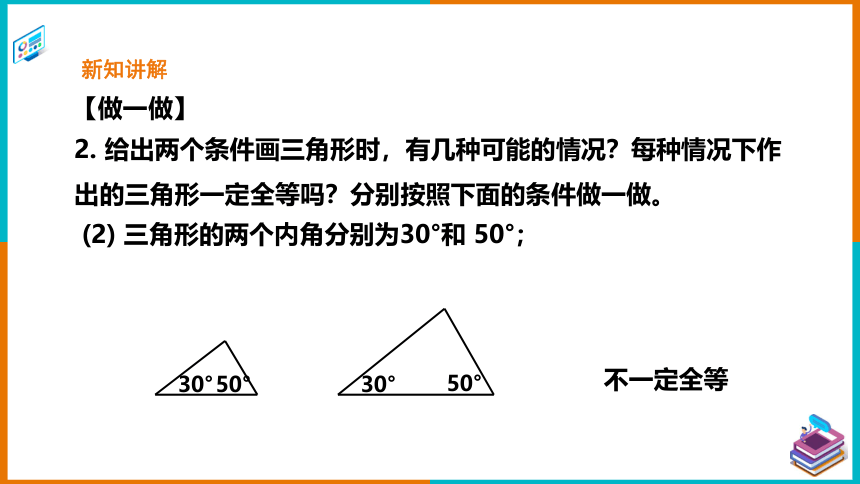
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(2) 三角形的两个内角分别为30°和 50°;
30°
30°
50°
50°
不一定全等
新知讲解
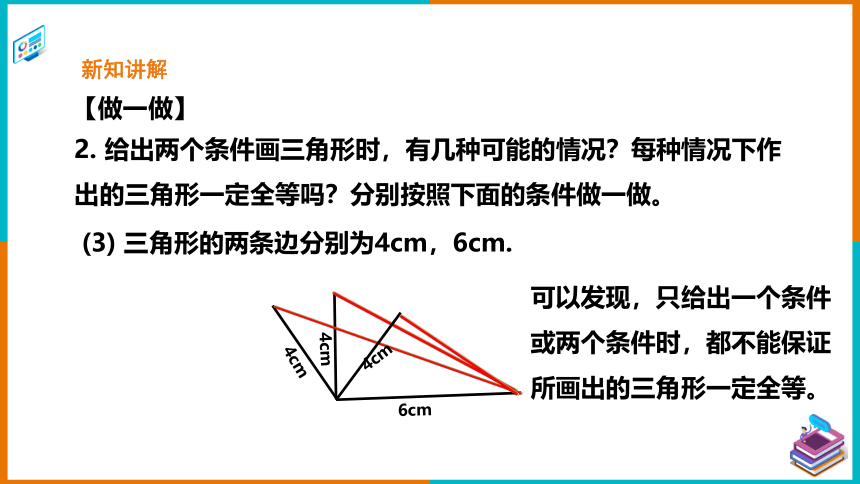
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(3) 三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
可以发现,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等。
新知讲解
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
(1)三个角;
(2)三条边;
(3)两角一边;
(4)两边一角.
有四种可能:
新知讲解
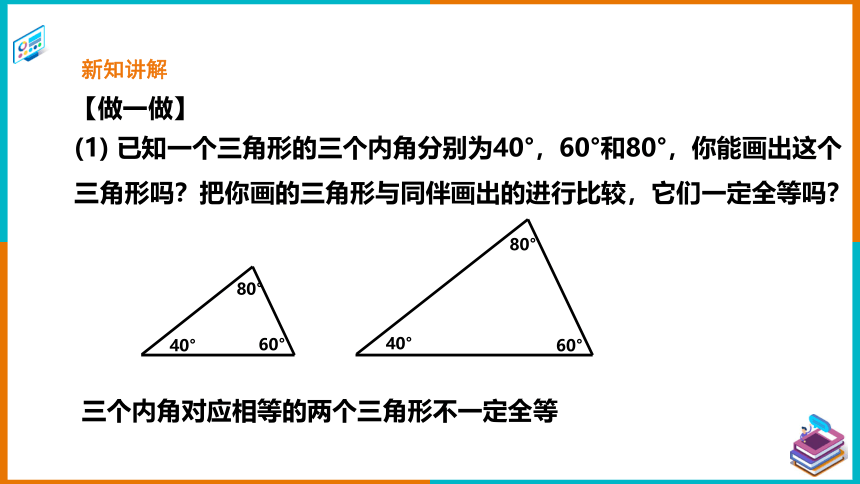
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三个内角对应相等的两个三角形不一定全等
40°
80°
60°
40°
80°
60°
新知讲解
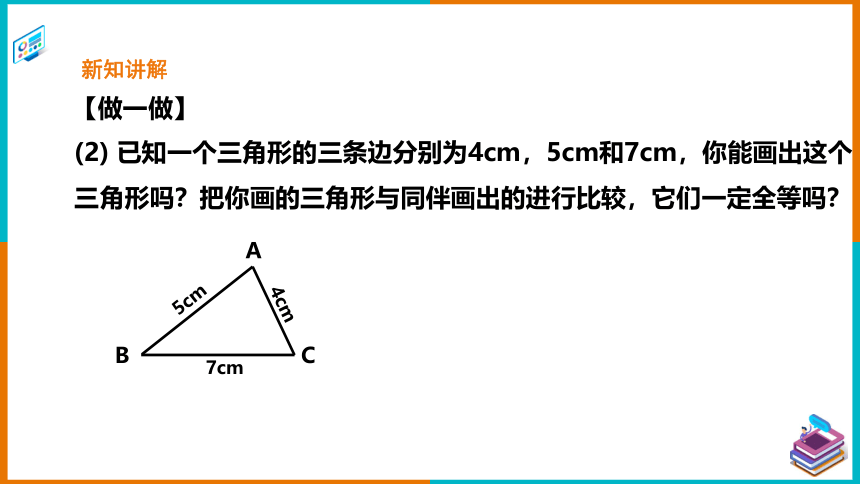
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
5cm
4cm
7cm
A
B
C
新知讲解
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三条边对应相等的两个三角形一定全等。
B'
C'
A'
作法:
(1)画B'C'=BC;
(2)分别以B'C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A‘;
(3)连接线段A'B',A'C'
新知讲解
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
【总结归纳】
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
新知讲解
【例】已知:如图,AB=AC,AD=AE,BD=CE.
证明:∠BAC=∠DAE.
在△ABD和△ACE中,因为
所以△ABD≌△ACE(SSS),
所以∠BAD=∠CAE.
所以∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
新知讲解
由上面的结论可知,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性.
新知讲解
如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
它的形状是可以改变的,
因此四边形具有不稳定性.
新知讲解
在生活中,我们经常会看到应用三角形稳定性的例子.
新知讲解
你还能举出一些其他的例子吗?
课堂练习
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC
B. △ABE≌△ADE
C. △CBE≌△CDE
D. 以上选项都对
B
课堂练习
2.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
课堂练习
3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS).所以∠A=∠D.
拓展提高
4.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.
试判断AC与BC的位置关系,并说明理由.
拓展提高
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,CF=CE+EF,所以AE=CF.
在△ACE和△CBF中,
所以△ACE≌△CBF(SSS).所以∠CAE=∠BCF.
因为∠CAE+∠ACE=90°,
所以∠ACE+∠BCF=90°.
所以∠ACB=90°.所以AC⊥BC.
课堂总结
这节课你学到了什么?
1. 三角形全等的条件:三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
板书设计
1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”。
2.三角形具有稳定性。
作业布置
课本 习题4.6
利用“角边角”判定三角形全等
新知导入
A
B
C
D
【思考】已知如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
解:△ABC≌△DCB,
理由: 在△ABC和△DCB中
AB =___ ( )
AC =___ ( )
___=___ ( )
∴△ABC ≌△DCB( )
已知
已知
公共边
CD
DB
BC
CB
SSS
新知导入
有一块三角形纸片撕去了一个角,要去剪一块新的,如果你手头没有测量的仪器,你能保证新剪的纸片形状、大小和原来的一样吗
【思考】 判别三角形全等是不是还有其他方法呢
新知讲解
【做一做】
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
新知讲解
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法1:先画出BC=2 cm,然后画∠B=80°,最后画∠C=60°.
新知讲解
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法2:先画出∠B=80°,然后画BC=2 cm,最后画∠C=60°.
新知讲解
改变角度和边长,你能得到同样的结论吗
改变角度和边长,所画的三角形仍然全等。
同学把画出的三角形剪下来,与同小组比较,看是否重合.
画出的三角形都全等.
新知讲解
【总结归纳】
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
新知讲解
【例】如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,
证明:AD=AE.
A
B
C
D
E
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
∴AD=AE.
新知讲解
【总结提升】
在说明两个三角形全等需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;(6)直角都相等;
(7)全等三角形对应角相等;(8)第三角代换,即等量代换等.
课堂练习
1.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )。
A .8
B .7
C .6
D .5
A
B
C
D
E
F
B
课堂练习
2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A. 10
B. 6
C. 5
D. 4.5
C
A
B
C
D
E
F
课堂练习
1
2
A
B
C
D
3.如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
证明:∵ AD是∠BAC的角平分线
∴ AB=AC(全等三角形对应边相等)
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∴ △ABD≌△ACD(ASA)
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
拓展提高
4.如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
解:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在ADF和△CBE中,
∵
∴△ADF≌△CBE(ASA).
∠A= ∠C
AF=CE
∠DFA= ∠BEC
课堂总结
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另一种方法,它是:
两角和它们的夹边对应相等的两个三角形全等(ASA)
再加上前面学的(SSS),证明两个三角形全等共有两种方法,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
板书设计
角边角:两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
作业布置
课本 习题4.7
利用“角角边”判定三角形全等
新知导入
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:带1去,因为有两角且夹边相等的两个三角形全等.
新知讲解
议一议
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?
你能将它转化为“做一做”中的条件吗?
新知讲解
【做一做】
如果“两角及一边”条件中的边是其中一角的对边,比如三角形的两个内角分别是60°和80°,其中60°角所对的边为2cm。
2cm
80°
60°
新知讲解
【做一做】
(1)如果80°角所对的边是2 cm,你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
画的三角形全等
新知讲解
【做一做】
(2)如果60°角所对的边是2 cm,你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
画的三角形全等
新知讲解
【思考】
通过刚才的画图,你能得到什么结论?
2cm
80°
60°
2cm
80°
60°
两角和其中一角的对边对应相等的两个三角形全等。
新知讲解
【总结归纳】
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E ,
AB=DE
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
新知讲解
【例】如图,AD是△ABC的中线,过点C,B分别作AD的垂线CF,BE.
证明:BE=CF.
证明:∵AD是△ABC的中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,
∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).∴BE=CF.
新知讲解
【思考】如图所示,AB与CD相交于点O,O是AB的中点,∠A=∠B, △AOC与△BOD全等吗?
A
B
C
D
O
因为点O是AB的中点,所以OA=OB.又已知∠A=∠B,且∠AOC=∠BOD,所以△AOC≌△BOD。
你能理解其中的意思吗?
新知讲解
利用两个三角形全等解决问题,先根据已知条件或要说明的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去说明什么条件,简言之:即综合利用分析法和综合法寻找解题的途径.
【总结归纳】
新知讲解
【议一议】
我们已经学习了“SSS”“ASA”“AAS”三种判定方法,那么这三种判定方法在判断两个三角形全等时要注意什么
1.判定两个三角形全等的条件一定要具备三对“对应相等”.
2.要判定两个三角形全等时,边和角“对应相等”,而不是“分别相等”.即:两个三角形中相等的边和角必须有相同的顺序.
3.注意题目中隐含的条件,如:公共边.
课堂练习
1.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对
B.2对
C.3对
D.4对
B
课堂练习
2.如图,AB∥CD,且AB=CD,AC与BD相交于点E,则△ABE≌△CDE的根据是( )
A. 只能用ASA
B. 只能用SSS
C. 只能用AAS
D. 用ASA或AAS
A
B
D
C
E
D
课堂练习
3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 证明:AB=AD.
A
C
D
B
1
2
证明:∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
拓展提高
4.已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高.
证明AD= A′D′ .
A
B
C
D
A ′
B ′
C ′
D ′
拓展提高
证明:因为△ABC ≌△A′B′C′ ,
所以AB=A'B'(全等三角形对应边相等),∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=AB(已证),
所以△ABD≌△A'B'D'.所以AD=A'D'.
课堂总结
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
这节课你学会了什么?
三角形全等判定方法3:
板书设计
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E ,
AB=DE
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
作业布置
课本 习题4.7
利用“边角边”判定三角形全等
新知导入
到目前为止,我们已学过哪些方法判定两三角形全等?
边边边(SSS)
角边角(ASA)
角角边(AAS)
新知导入
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
两边及夹角或两边及其一边的对角
那么有几种可能的情况呢?
新知讲解
如果“两边及一角”条件中的角是两边的夹角,比如三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?动手试一试.
40°
2.5cm
3.5cm
【做一做】
新知讲解
如果“两边及一角”条件中的角是两边的夹角,比如三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
【做一做】
2.5cm
3.5cm
40°
你画的三角形与同伴画的一定全等吗?
画的三角形是全等的
新知讲解
改变上述条件中的角度和边长,再试一试。
若两边的夹角为20°,画一个三角形.试一试,情况会怎样呢?
画的三角形仍然是全等的
新知讲解
由此可得结论:__________________________________________,
两边及其夹角分别相等的两个三角形全等
简写成_________或________。
边角边
SAS
在△ABC和△DEF中,
AB=DE,
∠B=∠E,
BC=EF ,
∴△ABC≌△DEF(SAS).
几何语言:
A
B
C
D
E
F
新知讲解
【例】已知:AD=CD,DB平分∠ADC ,证明:∠A=∠C.
A
B
C
D
1
2
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AD=CD (已知),
∠1=∠2 (已证),
BD=BD (公共边),
∴∠A=∠C.
∵DB 平分∠ ADC,
∴∠1=∠2.
新知讲解
如果“两边及一角”条件中的是其中一边的对角,比如两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40° ,情况会怎样呢?
动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
新知讲解
如果“两边及一角”条件中的是其中一边的对角,比如两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40° ,情况会怎样呢?
动手画一画,你发现了什么?
注意:两边分别相等且其中一组等边的对角分别相等,那么这两个三角形不一定全等。
课堂练习
1.下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
课堂练习
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
课堂练习
3.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.
证明:△ADF≌△BCE.
证明:∵AE=BF,
∵AF=AE+EF=BF+EF=BE.
在△ADF和△BCE中,
∵△ADF≌△BCE(SAS).
AD=BC
∠A=∠B
AF=BE
拓展提高
4.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点,
证明:DM=DN.
在△ABD与△CBD中
证明:
CA=CB (已知)
AD=BD (已知)
CD=CD (公共边)
∴△ACD≌△BCD(SSS)
连接CD,如图所示;
∴∠A=∠B
又∵M,N分别是CA,CB的中点,∴AM=BN
拓展提高
在△AMD与△BND中
AM=BN (已证)
∠A=∠B (已证)
AD=BD (已知)
∴△AMD≌△BND(SAS)
∴DM=DN.
4.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点,
证明:DM=DN.
课堂总结
1. 今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2. 通过这节课,判定三角形全等的条件有哪些?
SSS,SAS,ASA,AAS
3.在这四种说明三角形全等的条件中,你发现了什么?
至少有一个条件:边相等
注意:“边边角”不能判定两个三角形全等。
板书设计
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
注意:1.已知两边,必须找“夹角”。
2. 已知一角和这角的一夹边,必须找这角的另一夹边 。
北师大版 初中数学
探索三角形全等的条件
利用“边边边”判定三角形全等
北师大版 初中数学
新知导入
1. 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
A
B
C
D
E
F
2.已知△ABC ≌△DEF,找出其中相等的边与角.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
新知讲解
【思考】
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?……
新知讲解
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
①只给一条边:
不一定全等
新知讲解
②只给一个角:
60°
60°
60°
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
新知讲解
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(1) 三角形的一个内角为30°,一条边为3cm;
30°
30°
30°
不一定全等
新知讲解
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(2) 三角形的两个内角分别为30°和 50°;
30°
30°
50°
50°
不一定全等
新知讲解
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(3) 三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
可以发现,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等。
新知讲解
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
(1)三个角;
(2)三条边;
(3)两角一边;
(4)两边一角.
有四种可能:
新知讲解
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三个内角对应相等的两个三角形不一定全等
40°
80°
60°
40°
80°
60°
新知讲解
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
5cm
4cm
7cm
A
B
C
新知讲解
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三条边对应相等的两个三角形一定全等。
B'
C'
A'
作法:
(1)画B'C'=BC;
(2)分别以B'C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A‘;
(3)连接线段A'B',A'C'
新知讲解
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
【总结归纳】
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
新知讲解
【例】已知:如图,AB=AC,AD=AE,BD=CE.
证明:∠BAC=∠DAE.
在△ABD和△ACE中,因为
所以△ABD≌△ACE(SSS),
所以∠BAD=∠CAE.
所以∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
新知讲解
由上面的结论可知,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性.
新知讲解
如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
它的形状是可以改变的,
因此四边形具有不稳定性.
新知讲解
在生活中,我们经常会看到应用三角形稳定性的例子.
新知讲解
你还能举出一些其他的例子吗?
课堂练习
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC
B. △ABE≌△ADE
C. △CBE≌△CDE
D. 以上选项都对
B
课堂练习
2.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
课堂练习
3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS).所以∠A=∠D.
拓展提高
4.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.
试判断AC与BC的位置关系,并说明理由.
拓展提高
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,CF=CE+EF,所以AE=CF.
在△ACE和△CBF中,
所以△ACE≌△CBF(SSS).所以∠CAE=∠BCF.
因为∠CAE+∠ACE=90°,
所以∠ACE+∠BCF=90°.
所以∠ACB=90°.所以AC⊥BC.
课堂总结
这节课你学到了什么?
1. 三角形全等的条件:三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
板书设计
1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”。
2.三角形具有稳定性。
作业布置
课本 习题4.6
利用“角边角”判定三角形全等
新知导入
A
B
C
D
【思考】已知如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
解:△ABC≌△DCB,
理由: 在△ABC和△DCB中
AB =___ ( )
AC =___ ( )
___=___ ( )
∴△ABC ≌△DCB( )
已知
已知
公共边
CD
DB
BC
CB
SSS
新知导入
有一块三角形纸片撕去了一个角,要去剪一块新的,如果你手头没有测量的仪器,你能保证新剪的纸片形状、大小和原来的一样吗
【思考】 判别三角形全等是不是还有其他方法呢
新知讲解
【做一做】
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
新知讲解
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法1:先画出BC=2 cm,然后画∠B=80°,最后画∠C=60°.
新知讲解
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法2:先画出∠B=80°,然后画BC=2 cm,最后画∠C=60°.
新知讲解
改变角度和边长,你能得到同样的结论吗
改变角度和边长,所画的三角形仍然全等。
同学把画出的三角形剪下来,与同小组比较,看是否重合.
画出的三角形都全等.
新知讲解
【总结归纳】
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
新知讲解
【例】如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,
证明:AD=AE.
A
B
C
D
E
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
∴AD=AE.
新知讲解
【总结提升】
在说明两个三角形全等需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;(6)直角都相等;
(7)全等三角形对应角相等;(8)第三角代换,即等量代换等.
课堂练习
1.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )。
A .8
B .7
C .6
D .5
A
B
C
D
E
F
B
课堂练习
2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A. 10
B. 6
C. 5
D. 4.5
C
A
B
C
D
E
F
课堂练习
1
2
A
B
C
D
3.如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
证明:∵ AD是∠BAC的角平分线
∴ AB=AC(全等三角形对应边相等)
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∴ △ABD≌△ACD(ASA)
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
拓展提高
4.如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
解:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在ADF和△CBE中,
∵
∴△ADF≌△CBE(ASA).
∠A= ∠C
AF=CE
∠DFA= ∠BEC
课堂总结
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另一种方法,它是:
两角和它们的夹边对应相等的两个三角形全等(ASA)
再加上前面学的(SSS),证明两个三角形全等共有两种方法,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
板书设计
角边角:两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
作业布置
课本 习题4.7
利用“角角边”判定三角形全等
新知导入
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:带1去,因为有两角且夹边相等的两个三角形全等.
新知讲解
议一议
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?
你能将它转化为“做一做”中的条件吗?
新知讲解
【做一做】
如果“两角及一边”条件中的边是其中一角的对边,比如三角形的两个内角分别是60°和80°,其中60°角所对的边为2cm。
2cm
80°
60°
新知讲解
【做一做】
(1)如果80°角所对的边是2 cm,你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
画的三角形全等
新知讲解
【做一做】
(2)如果60°角所对的边是2 cm,你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
画的三角形全等
新知讲解
【思考】
通过刚才的画图,你能得到什么结论?
2cm
80°
60°
2cm
80°
60°
两角和其中一角的对边对应相等的两个三角形全等。
新知讲解
【总结归纳】
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E ,
AB=DE
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
新知讲解
【例】如图,AD是△ABC的中线,过点C,B分别作AD的垂线CF,BE.
证明:BE=CF.
证明:∵AD是△ABC的中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,
∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).∴BE=CF.
新知讲解
【思考】如图所示,AB与CD相交于点O,O是AB的中点,∠A=∠B, △AOC与△BOD全等吗?
A
B
C
D
O
因为点O是AB的中点,所以OA=OB.又已知∠A=∠B,且∠AOC=∠BOD,所以△AOC≌△BOD。
你能理解其中的意思吗?
新知讲解
利用两个三角形全等解决问题,先根据已知条件或要说明的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去说明什么条件,简言之:即综合利用分析法和综合法寻找解题的途径.
【总结归纳】
新知讲解
【议一议】
我们已经学习了“SSS”“ASA”“AAS”三种判定方法,那么这三种判定方法在判断两个三角形全等时要注意什么
1.判定两个三角形全等的条件一定要具备三对“对应相等”.
2.要判定两个三角形全等时,边和角“对应相等”,而不是“分别相等”.即:两个三角形中相等的边和角必须有相同的顺序.
3.注意题目中隐含的条件,如:公共边.
课堂练习
1.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对
B.2对
C.3对
D.4对
B
课堂练习
2.如图,AB∥CD,且AB=CD,AC与BD相交于点E,则△ABE≌△CDE的根据是( )
A. 只能用ASA
B. 只能用SSS
C. 只能用AAS
D. 用ASA或AAS
A
B
D
C
E
D
课堂练习
3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 证明:AB=AD.
A
C
D
B
1
2
证明:∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
拓展提高
4.已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高.
证明AD= A′D′ .
A
B
C
D
A ′
B ′
C ′
D ′
拓展提高
证明:因为△ABC ≌△A′B′C′ ,
所以AB=A'B'(全等三角形对应边相等),∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=AB(已证),
所以△ABD≌△A'B'D'.所以AD=A'D'.
课堂总结
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
这节课你学会了什么?
三角形全等判定方法3:
板书设计
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”.
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E ,
AB=DE
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
作业布置
课本 习题4.7
利用“边角边”判定三角形全等
新知导入
到目前为止,我们已学过哪些方法判定两三角形全等?
边边边(SSS)
角边角(ASA)
角角边(AAS)
新知导入
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
两边及夹角或两边及其一边的对角
那么有几种可能的情况呢?
新知讲解
如果“两边及一角”条件中的角是两边的夹角,比如三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?动手试一试.
40°
2.5cm
3.5cm
【做一做】
新知讲解
如果“两边及一角”条件中的角是两边的夹角,比如三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
【做一做】
2.5cm
3.5cm
40°
你画的三角形与同伴画的一定全等吗?
画的三角形是全等的
新知讲解
改变上述条件中的角度和边长,再试一试。
若两边的夹角为20°,画一个三角形.试一试,情况会怎样呢?
画的三角形仍然是全等的
新知讲解
由此可得结论:__________________________________________,
两边及其夹角分别相等的两个三角形全等
简写成_________或________。
边角边
SAS
在△ABC和△DEF中,
AB=DE,
∠B=∠E,
BC=EF ,
∴△ABC≌△DEF(SAS).
几何语言:
A
B
C
D
E
F
新知讲解
【例】已知:AD=CD,DB平分∠ADC ,证明:∠A=∠C.
A
B
C
D
1
2
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AD=CD (已知),
∠1=∠2 (已证),
BD=BD (公共边),
∴∠A=∠C.
∵DB 平分∠ ADC,
∴∠1=∠2.
新知讲解
如果“两边及一角”条件中的是其中一边的对角,比如两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40° ,情况会怎样呢?
动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
新知讲解
如果“两边及一角”条件中的是其中一边的对角,比如两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40° ,情况会怎样呢?
动手画一画,你发现了什么?
注意:两边分别相等且其中一组等边的对角分别相等,那么这两个三角形不一定全等。
课堂练习
1.下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
课堂练习
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
课堂练习
3.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.
证明:△ADF≌△BCE.
证明:∵AE=BF,
∵AF=AE+EF=BF+EF=BE.
在△ADF和△BCE中,
∵△ADF≌△BCE(SAS).
AD=BC
∠A=∠B
AF=BE
拓展提高
4.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点,
证明:DM=DN.
在△ABD与△CBD中
证明:
CA=CB (已知)
AD=BD (已知)
CD=CD (公共边)
∴△ACD≌△BCD(SSS)
连接CD,如图所示;
∴∠A=∠B
又∵M,N分别是CA,CB的中点,∴AM=BN
拓展提高
在△AMD与△BND中
AM=BN (已证)
∠A=∠B (已证)
AD=BD (已知)
∴△AMD≌△BND(SAS)
∴DM=DN.
4.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点,
证明:DM=DN.
课堂总结
1. 今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2. 通过这节课,判定三角形全等的条件有哪些?
SSS,SAS,ASA,AAS
3.在这四种说明三角形全等的条件中,你发现了什么?
至少有一个条件:边相等
注意:“边边角”不能判定两个三角形全等。
板书设计
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
注意:1.已知两边,必须找“夹角”。
2. 已知一角和这角的一夹边,必须找这角的另一夹边 。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
