北师大版七年级下册数学6.2 概率的稳定性 课件(共43张PPT)
文档属性
| 名称 | 北师大版七年级下册数学6.2 概率的稳定性 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 449.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 07:17:37 | ||
图片预览










文档简介
(共43张PPT)
北师大版 初中数学
概率的稳定性
抛图钉试验
北师大版 初中数学
导入
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下。你认为钉尖朝上和
钉尖朝下的可能性一样
大吗
小明和小丽在玩抛图钉游戏
导入
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的。
我的直觉跟你一样,但我不知道对不对。
不妨让我们用试验来验证吧!
新课
(1)两人一组做 20 次掷图钉的游戏,并将数据记录在下表中:
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
新知讲解
注意事项:
1.做试验一定要注意安全,不要受伤.
2.图钉必须从同一高度自由落下,保证着地时的随机性和试验的
可重复操作性;
3.两人一组要进行适当的分工.
新知讲解
【思考】什么叫做频率?
定义:在n次重复试验中,不确定事件A发生了m次,则比值 称为事件 A发生的频率.
新知讲解
【例】在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是________.
10
新知讲解
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
11
26
48
80
92
124
141
171
198
213
239
0.55
0.65
0.6
0.67
0.58
0.62
0.59
0.61
0.62
0.59
0.60
新知讲解
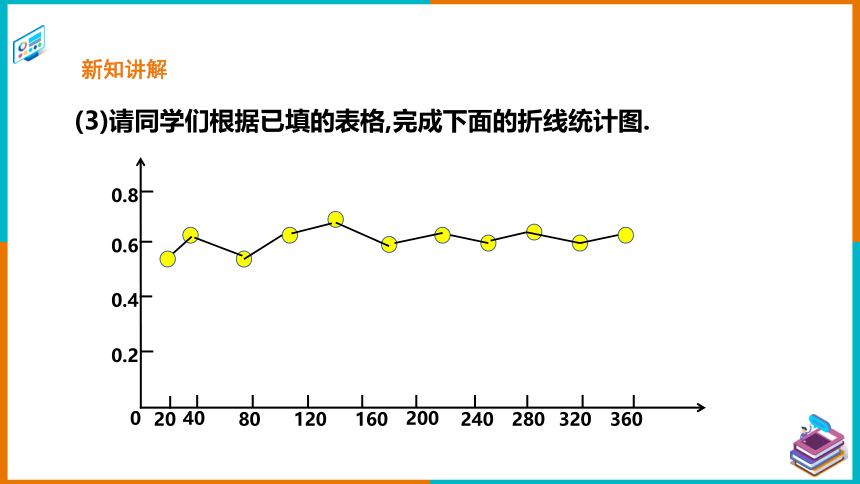
(3)请同学们根据已填的表格,完成下面的折线统计图.
0
20
40
80
120
160
200
240
280
320
360
0.2
0.4
0.6
0.8
新知讲解
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
随机事件发生的频率具有稳定性,试验次数越多,稳定性越明显,频率就越接近于一个常数.
议一议
(1) 通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎么想的?
(2) 小军与小凡一起做了1000 次掷图钉的试验,其中有640次钉尖朝上,据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.你同意他们的说法吗?
新课
新课
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
拓展提高
4.在地面上有一组平行线,相邻两条平行线的距离都是5 cm,将长为3 cm的针任意投向这组平行线,下表是九年级某班同学合作完成投针试验后统计的数据.
投针次数 100 600 1000 2500 3500 5000
针与线相交的次数 48 281 454 861 1371 1901
相交的频率
拓展提高
(1)分别求出表格中各相交频率的大小;
投针次数 100 600 1000 2500 3500 5000
针与线相交的次数 48 281 454 861 1371 1901
相交的频率
0.48
0.468
0.454
0.344
0.392
0.38
拓展提高
(2)在试验次数很大时,频率应稳定于 ;
(3)根据表格中试验频率的变化,说明在题设的情况下,针与平行线相交与不相交的可能性.
(3)针与平行线相交的可能性为0.4,不相交的可能性为0.6.
0.40
课堂总结
1.在n次重复试验中,不确定事件A发生了m次,则比值 称为事件A发生的频率.
2.在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
这节课你学到了什么?
板书设计
1.频率的试验(抛图钉试验)
2.频率及其稳定性:
在大量重复试验的情况下,事件的频率会呈现稳定性,即频率会在一个常数附近摆动.随着试验次数的增加,摆动的幅度有越来越小的趋势.
抛硬币试验
新知导入
1.思考回答下列问题。
(1)举例说明什么是必然事件.
(2)举例说明什么是不可能事件.
(3)举例说明什么是不确定事件.
新知导入
2.结合图形完成下面问题.
(1)明天会下雨是什么事件 可能性多大
(2)太阳从东方升起是什么事件 可能性大吗
(3)如果随机抛出一枚骰子,抛出的点数会是7吗 这是什么事件 可能性大吗
不确定事件
不可能事件
不可能事件
新知讲解
你认为一枚硬币抛出之后会怎么样 那么这几种情况哪种情况的可能性更大一些呢
新知讲解
会出现正面或者反面。
出现正面或者反面的可能性应一样大。
让我们做实验来验证一下。
新知讲解
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(提示:硬币是均匀硬币,要从同一高度任意掷出)
20
10
10
0.5
0.5
新知讲解
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
10
10
0.5
0.5
19
21
0.48
0.52
33
27
0.55
0.45
39
41
0.49
0.51
53
47
0.53
0.47
59
61
0.49
0.51
75
65
0.54
0.46
78
82
0.49
0.51
90
90
0.5
0.5
106
94
0.53
0.47
新知讲解
(3)根据上表,完成下面的折线统计图.
20
40
60
80
100
120
140
160
180
200
0.5
0
1.0
0.2
0.7
频率
新知讲解
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
新知讲解
200个数据是不是太少了,能说明问题吗
我们所做的试验不能说是大量的.但是有些人的确做了很多次.
试验者 投掷 次数n 正面出现 次数m 正面出现
的频率 m/n
布 丰 4040 2048 0.5069
德 摩根 4092 2048 0.5005
费 勒 10000 4979 0.4979
新知讲解
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
维 尼 30000 14994 0.4998
罗曼诺 夫斯基 80640 39699 0.4923
试验者 投掷 次数n 正面出现 次数m 正面出现
的频率m/n
新知讲解
(5)表中的数据支持你发现的规律吗
上表中正面出现的频率都接近0.5,这说明当抛硬币的次数足够多的时候,抛硬币正面和反面朝上的频率基本是一样的.
新知讲解
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
【总结归纳】
新知讲解
由于事件A发生的频率表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
【总结归纳】
新知讲解
【想一想】
事件A发生的概率P(A)的取值范围是什么?
必然事件发生的概率是多少?
不可能事件发生的概率又是多少
新知讲解
从定义可以得到二者的联系,可用大量重复试验中事件发生的频率来估计事件发生的概率.另一方面,大量重复试验中事件发生的频率稳定在某个常数(事件发生的概率)附近,说明概率是个定值,而频率随不同试验次数而有所不同,是概率的近似值,二者不能简单地等同.通过定义可以看出事件A发生的概率P(A)的取值范围是0≤P(A)≤1.
【总结归纳】
新知讲解
必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数.
新知讲解
频率与概率的区别与联系.
1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值.
新知讲解
【拓展提高】频率与概率的区别与联系.
1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值.
习题
1. 小凡做了 5 次抛掷均匀硬币的试验,其中有 3 次正面朝上,2 次正面朝下,他认为正面朝上的概率大约为 ,朝下的概率约为 ,你同意他的观点吗?你认为他再多做一些试验,结果还是这样吗?
解:不同意,试验次数增加到足够多时,结果会发生改变.
习题
2.抛掷一枚均匀的硬币,正面朝上的概率为 ,
那么,抛掷 100 次硬币,你能保证恰好 50 次正面朝上吗?与同伴进行交流.
解:不能
拓展提高
4.掷一枚质地均匀的骰子.
(1)会出现哪些可能的结果
(2)掷出点数为1与掷出点数为2的可能性相同吗 掷出点数为1与掷出点数为3的可能性相同吗
(3)每种结果出现的可能性相同吗 你是怎样做的
拓展提高
解:(1)投掷一枚质地均匀的骰子,向上的面的点数可能是1,2,3,4,5,6,这6种结果.
(2)掷出点数为1与掷出点数为2的可能性相同;掷出点数为1与掷出点数为3的可能性相同.
(3)每种结果出现的可能性相同;通过大量的试验进行验证.
课堂总结
1.在试验次数很大时,事件发生的频率,都会在一个常数附近摆动,这个性质称为:频率的稳定性.
2.我们把这个刻画事件A发生的可能性大小的数值,称为事件A的概率,记为P(A).
3.一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;不可能事件发生的概率为0;不确定事件A发生的概率P(A)是0与1之间的一个常数.
板书设计
1.抛硬币试验
2.无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
3.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数.
北师大版 初中数学
概率的稳定性
抛图钉试验
北师大版 初中数学
导入
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下。你认为钉尖朝上和
钉尖朝下的可能性一样
大吗
小明和小丽在玩抛图钉游戏
导入
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的。
我的直觉跟你一样,但我不知道对不对。
不妨让我们用试验来验证吧!
新课
(1)两人一组做 20 次掷图钉的游戏,并将数据记录在下表中:
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
新知讲解
注意事项:
1.做试验一定要注意安全,不要受伤.
2.图钉必须从同一高度自由落下,保证着地时的随机性和试验的
可重复操作性;
3.两人一组要进行适当的分工.
新知讲解
【思考】什么叫做频率?
定义:在n次重复试验中,不确定事件A发生了m次,则比值 称为事件 A发生的频率.
新知讲解
【例】在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是________.
10
新知讲解
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
11
26
48
80
92
124
141
171
198
213
239
0.55
0.65
0.6
0.67
0.58
0.62
0.59
0.61
0.62
0.59
0.60
新知讲解
(3)请同学们根据已填的表格,完成下面的折线统计图.
0
20
40
80
120
160
200
240
280
320
360
0.2
0.4
0.6
0.8
新知讲解
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
随机事件发生的频率具有稳定性,试验次数越多,稳定性越明显,频率就越接近于一个常数.
议一议
(1) 通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎么想的?
(2) 小军与小凡一起做了1000 次掷图钉的试验,其中有640次钉尖朝上,据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.你同意他们的说法吗?
新课
新课
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
拓展提高
4.在地面上有一组平行线,相邻两条平行线的距离都是5 cm,将长为3 cm的针任意投向这组平行线,下表是九年级某班同学合作完成投针试验后统计的数据.
投针次数 100 600 1000 2500 3500 5000
针与线相交的次数 48 281 454 861 1371 1901
相交的频率
拓展提高
(1)分别求出表格中各相交频率的大小;
投针次数 100 600 1000 2500 3500 5000
针与线相交的次数 48 281 454 861 1371 1901
相交的频率
0.48
0.468
0.454
0.344
0.392
0.38
拓展提高
(2)在试验次数很大时,频率应稳定于 ;
(3)根据表格中试验频率的变化,说明在题设的情况下,针与平行线相交与不相交的可能性.
(3)针与平行线相交的可能性为0.4,不相交的可能性为0.6.
0.40
课堂总结
1.在n次重复试验中,不确定事件A发生了m次,则比值 称为事件A发生的频率.
2.在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
这节课你学到了什么?
板书设计
1.频率的试验(抛图钉试验)
2.频率及其稳定性:
在大量重复试验的情况下,事件的频率会呈现稳定性,即频率会在一个常数附近摆动.随着试验次数的增加,摆动的幅度有越来越小的趋势.
抛硬币试验
新知导入
1.思考回答下列问题。
(1)举例说明什么是必然事件.
(2)举例说明什么是不可能事件.
(3)举例说明什么是不确定事件.
新知导入
2.结合图形完成下面问题.
(1)明天会下雨是什么事件 可能性多大
(2)太阳从东方升起是什么事件 可能性大吗
(3)如果随机抛出一枚骰子,抛出的点数会是7吗 这是什么事件 可能性大吗
不确定事件
不可能事件
不可能事件
新知讲解
你认为一枚硬币抛出之后会怎么样 那么这几种情况哪种情况的可能性更大一些呢
新知讲解
会出现正面或者反面。
出现正面或者反面的可能性应一样大。
让我们做实验来验证一下。
新知讲解
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(提示:硬币是均匀硬币,要从同一高度任意掷出)
20
10
10
0.5
0.5
新知讲解
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
10
10
0.5
0.5
19
21
0.48
0.52
33
27
0.55
0.45
39
41
0.49
0.51
53
47
0.53
0.47
59
61
0.49
0.51
75
65
0.54
0.46
78
82
0.49
0.51
90
90
0.5
0.5
106
94
0.53
0.47
新知讲解
(3)根据上表,完成下面的折线统计图.
20
40
60
80
100
120
140
160
180
200
0.5
0
1.0
0.2
0.7
频率
新知讲解
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
新知讲解
200个数据是不是太少了,能说明问题吗
我们所做的试验不能说是大量的.但是有些人的确做了很多次.
试验者 投掷 次数n 正面出现 次数m 正面出现
的频率 m/n
布 丰 4040 2048 0.5069
德 摩根 4092 2048 0.5005
费 勒 10000 4979 0.4979
新知讲解
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
维 尼 30000 14994 0.4998
罗曼诺 夫斯基 80640 39699 0.4923
试验者 投掷 次数n 正面出现 次数m 正面出现
的频率m/n
新知讲解
(5)表中的数据支持你发现的规律吗
上表中正面出现的频率都接近0.5,这说明当抛硬币的次数足够多的时候,抛硬币正面和反面朝上的频率基本是一样的.
新知讲解
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
【总结归纳】
新知讲解
由于事件A发生的频率表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
【总结归纳】
新知讲解
【想一想】
事件A发生的概率P(A)的取值范围是什么?
必然事件发生的概率是多少?
不可能事件发生的概率又是多少
新知讲解
从定义可以得到二者的联系,可用大量重复试验中事件发生的频率来估计事件发生的概率.另一方面,大量重复试验中事件发生的频率稳定在某个常数(事件发生的概率)附近,说明概率是个定值,而频率随不同试验次数而有所不同,是概率的近似值,二者不能简单地等同.通过定义可以看出事件A发生的概率P(A)的取值范围是0≤P(A)≤1.
【总结归纳】
新知讲解
必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数.
新知讲解
频率与概率的区别与联系.
1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值.
新知讲解
【拓展提高】频率与概率的区别与联系.
1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值.
习题
1. 小凡做了 5 次抛掷均匀硬币的试验,其中有 3 次正面朝上,2 次正面朝下,他认为正面朝上的概率大约为 ,朝下的概率约为 ,你同意他的观点吗?你认为他再多做一些试验,结果还是这样吗?
解:不同意,试验次数增加到足够多时,结果会发生改变.
习题
2.抛掷一枚均匀的硬币,正面朝上的概率为 ,
那么,抛掷 100 次硬币,你能保证恰好 50 次正面朝上吗?与同伴进行交流.
解:不能
拓展提高
4.掷一枚质地均匀的骰子.
(1)会出现哪些可能的结果
(2)掷出点数为1与掷出点数为2的可能性相同吗 掷出点数为1与掷出点数为3的可能性相同吗
(3)每种结果出现的可能性相同吗 你是怎样做的
拓展提高
解:(1)投掷一枚质地均匀的骰子,向上的面的点数可能是1,2,3,4,5,6,这6种结果.
(2)掷出点数为1与掷出点数为2的可能性相同;掷出点数为1与掷出点数为3的可能性相同.
(3)每种结果出现的可能性相同;通过大量的试验进行验证.
课堂总结
1.在试验次数很大时,事件发生的频率,都会在一个常数附近摆动,这个性质称为:频率的稳定性.
2.我们把这个刻画事件A发生的可能性大小的数值,称为事件A的概率,记为P(A).
3.一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;不可能事件发生的概率为0;不确定事件A发生的概率P(A)是0与1之间的一个常数.
板书设计
1.抛硬币试验
2.无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
3.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
