五年级下册第三单元长方体和正方体的表面积阶段提升练习二人教版(含答案)
文档属性
| 名称 | 五年级下册第三单元长方体和正方体的表面积阶段提升练习二人教版(含答案) | 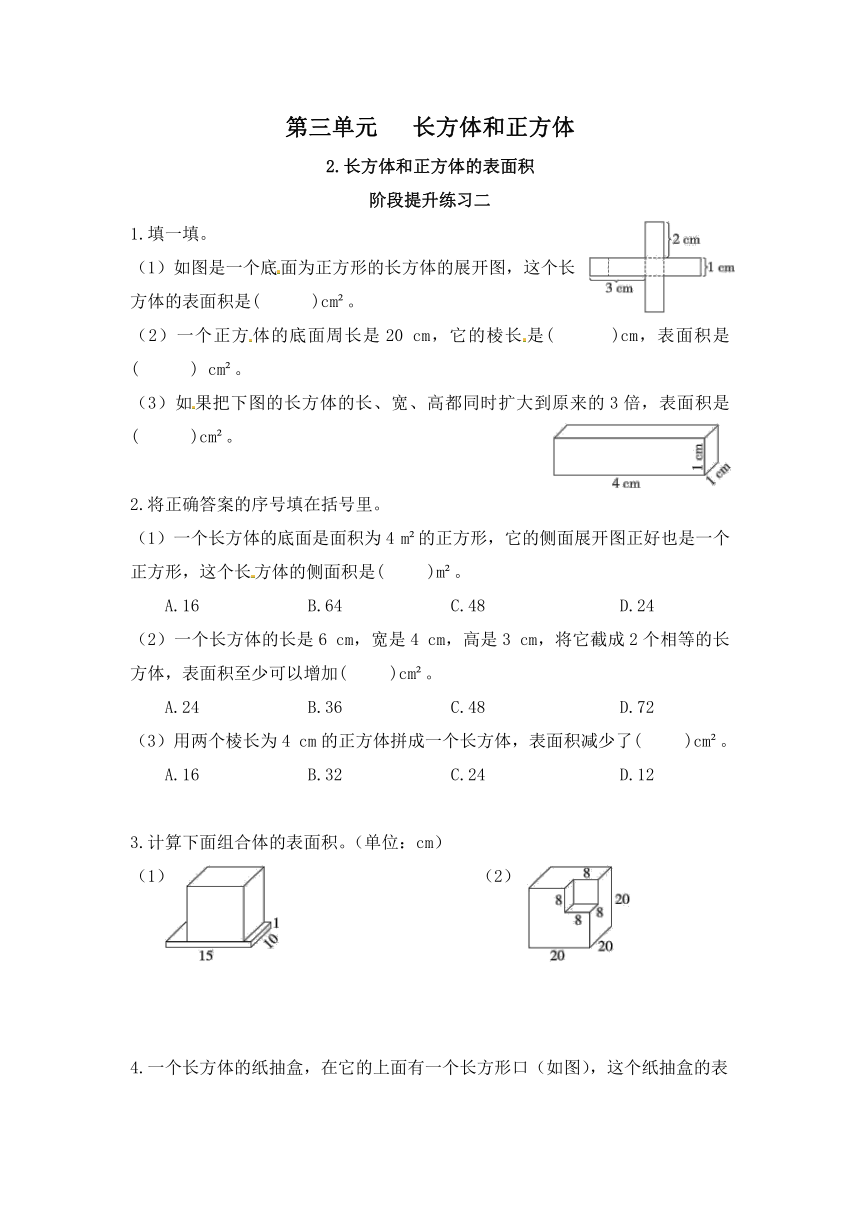 | |
| 格式 | docx | ||
| 文件大小 | 144.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 13:17:47 | ||
图片预览


文档简介
第三单元 长方体和正方体
2.长方体和正方体的表面积
阶段提升练习二
1.填一填。
(1)如图是一个底面为正方形的长方体的展开图,这个长方体的表面积是( )cm 。
(2)一个正方体的底面周长是20 cm,它的棱长是( )cm,表面积是( ) cm 。
(3)如果把下图的长方体的长、宽、高都同时扩大到原来的3倍,表面积是( )cm 。
2.将正确答案的序号填在括号里。
(1)一个长方体的底面是面积为4 m 的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )m 。
A.16 B.64 C.48 D.24
(2)一个长方体的长是6 cm,宽是4 cm,高是3 cm,将它截成2个相等的长方体,表面积至少可以增加( )cm 。
A.24 B.36 C.48 D.72
(3)用两个棱长为4 cm的正方体拼成一个长方体,表面积减少了( )cm 。
A.16 B.32 C.24 D.12
3.计算下面组合体的表面积。(单位:cm)
(1) (2)
4.一个长方体的纸抽盒,在它的上面有一个长方形口(如图),这个纸抽盒的表
面积是多少平方厘米?
5.如图,有5个正方体箱子放在墙角,每个正方体箱子的棱长是50 cm,露在外面的面的面积是多少平方厘米?
6.一个长方体茶叶盒,底面是边长0.6 dm的正方形,高是1.2 dm。现在要在四周贴上与长方体等高的商标纸,至少需要多少平方分米的商标纸?
7.锦绣小区有一个喷水池是长方体形状的,它的长是9 m,长是宽的1.2倍,深0.5 m。如果把喷水池的四周和底面贴上瓷砖,贴瓷砖的面积是多少平方米?
8.把一个长15 cm、宽12 cm、高8 cm 的长方体木块锯成两个完全一样的小长方体,怎样锯可以使这两个小长方体的表面积之和最大?这时每个小长方体的表面积是多少平方厘米?
9.娇娇就要过生日了,聪聪和明明都给娇娇买了一个生日礼物,都装在长4 dm 、宽2 dm、高3 dm的礼品盒中。售货员阿姨想把两个礼品盒放在一起包装。怎样包装才最节省包装纸呢?他们想出了如下三种方法。
你认为用谁的方法包装最节省包装纸?写出你的思考过程。
答案解析
1.(1)10
(2)5 150
(3)162
2.(1)B (2)A (3)B
3.(1)15×10×2+15×1×2+10×1×2=350(cm )
10×10×4=400(cm )
350+400=750(cm )
20×20×6=2400(cm )
4. (24×13+24×7+13×7)×2 14×2=1114(cm )
答:这个纸抽盒的表面积是1114 cm 。
5. 50×50×(3+5+2)=25000(cm )
答:露在外面的面的面积是25000 cm 。
0.6×1.2×4=2.88(dm )
答:至少需要2.88平方分米的商标纸。
9÷1.2=7.5(m)
9×7.5+(9×0.5+7.5×0.5)×2 =84(m )
答:贴瓷砖的面积是84 m 。
8.沿着平行于长15 cm、宽12 cm的面的方向锯。
8÷2=4(cm)
(15×4+12×4+15×12)×2=576(cm )
答:沿着平行于长15 cm、宽12 cm的面的方向锯,可以使这两个小长方体的表面积之和最大,这时每个小长方体的表面积是576 cm 。
9.用明明的方法包装最节省包装纸。售货员的方法节省了2个3 dm×2 dm的面,聪聪的方法节省了2个4 dm×2 dm的面,明明的方法节省了2个4 dm×3 dm 的面。明明节省的面积最大。
2.长方体和正方体的表面积
阶段提升练习二
1.填一填。
(1)如图是一个底面为正方形的长方体的展开图,这个长方体的表面积是( )cm 。
(2)一个正方体的底面周长是20 cm,它的棱长是( )cm,表面积是( ) cm 。
(3)如果把下图的长方体的长、宽、高都同时扩大到原来的3倍,表面积是( )cm 。
2.将正确答案的序号填在括号里。
(1)一个长方体的底面是面积为4 m 的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )m 。
A.16 B.64 C.48 D.24
(2)一个长方体的长是6 cm,宽是4 cm,高是3 cm,将它截成2个相等的长方体,表面积至少可以增加( )cm 。
A.24 B.36 C.48 D.72
(3)用两个棱长为4 cm的正方体拼成一个长方体,表面积减少了( )cm 。
A.16 B.32 C.24 D.12
3.计算下面组合体的表面积。(单位:cm)
(1) (2)
4.一个长方体的纸抽盒,在它的上面有一个长方形口(如图),这个纸抽盒的表
面积是多少平方厘米?
5.如图,有5个正方体箱子放在墙角,每个正方体箱子的棱长是50 cm,露在外面的面的面积是多少平方厘米?
6.一个长方体茶叶盒,底面是边长0.6 dm的正方形,高是1.2 dm。现在要在四周贴上与长方体等高的商标纸,至少需要多少平方分米的商标纸?
7.锦绣小区有一个喷水池是长方体形状的,它的长是9 m,长是宽的1.2倍,深0.5 m。如果把喷水池的四周和底面贴上瓷砖,贴瓷砖的面积是多少平方米?
8.把一个长15 cm、宽12 cm、高8 cm 的长方体木块锯成两个完全一样的小长方体,怎样锯可以使这两个小长方体的表面积之和最大?这时每个小长方体的表面积是多少平方厘米?
9.娇娇就要过生日了,聪聪和明明都给娇娇买了一个生日礼物,都装在长4 dm 、宽2 dm、高3 dm的礼品盒中。售货员阿姨想把两个礼品盒放在一起包装。怎样包装才最节省包装纸呢?他们想出了如下三种方法。
你认为用谁的方法包装最节省包装纸?写出你的思考过程。
答案解析
1.(1)10
(2)5 150
(3)162
2.(1)B (2)A (3)B
3.(1)15×10×2+15×1×2+10×1×2=350(cm )
10×10×4=400(cm )
350+400=750(cm )
20×20×6=2400(cm )
4. (24×13+24×7+13×7)×2 14×2=1114(cm )
答:这个纸抽盒的表面积是1114 cm 。
5. 50×50×(3+5+2)=25000(cm )
答:露在外面的面的面积是25000 cm 。
0.6×1.2×4=2.88(dm )
答:至少需要2.88平方分米的商标纸。
9÷1.2=7.5(m)
9×7.5+(9×0.5+7.5×0.5)×2 =84(m )
答:贴瓷砖的面积是84 m 。
8.沿着平行于长15 cm、宽12 cm的面的方向锯。
8÷2=4(cm)
(15×4+12×4+15×12)×2=576(cm )
答:沿着平行于长15 cm、宽12 cm的面的方向锯,可以使这两个小长方体的表面积之和最大,这时每个小长方体的表面积是576 cm 。
9.用明明的方法包装最节省包装纸。售货员的方法节省了2个3 dm×2 dm的面,聪聪的方法节省了2个4 dm×2 dm的面,明明的方法节省了2个4 dm×3 dm 的面。明明节省的面积最大。
