高中数学同步指导试卷苏教版(2019)必修第二册解三角形1(word版含解析)
文档属性
| 名称 | 高中数学同步指导试卷苏教版(2019)必修第二册解三角形1(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 902.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 21:22:09 | ||
图片预览




文档简介
高中数学同步指导试卷苏教版(2019)必修第二册解三角形
一、单选题
1.如图,某市人民广场正中央有一座铁塔,为了测量塔高AB,某人先在塔的正西方点C处测得塔项的仰角为45°,然后从点C处沿南偏东30°方向前进60到达点D处,在D处测得塔项的仰角为,则铁塔AB的高度是( )
A.50 B.30 C.25 D.15
2.我国南宋时期著名的数学家秦九韶在其著作《数书九章》中独立提出了一种求三角形面积的方法“三斜求积术”,即的面积,其中分别为的内角的对边,若,且,则的面积的最大值为( )
A. B. C. D.
3.在中,若,则∠C=( ).
A.60° B.120° C.135° D.150°
4.东寺塔和西寺塔为昆明市城中古景,分别位于昆明市南面的书林街和东寺街,一东一西隔街相望,距今已有1100多年历史,在二月的梅花和烟雨中,“双塔烟雨”成为明清时的“昆明八景”之一.东寺塔基座为正方形,塔身有13级,塔顶四角立有四只铜皮做成的鸟,俗称金鸡,所以也有“金鸡塔”之称.如图,从东到西的公路上有相距80(单位:)的两个观测点,在点测得塔在北偏东60°的点处,在点测得塔在北偏西30°,塔顶的仰角为45°,则塔的高度约为( )
A. B. C. D.
5.的内角A,B,C的对边分别为a,b,c,若,则为( )
A.等腰非等边三角形 B.直角三角形
C.钝角三角形 D.等边三角形
6.的内角A,B,C的对边分别为a,b,c,已知,,则的面积为( )
A. B.
C. D.
7.设的三个内角满足,又,则这个三角形的形状是( )
A.直角三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
8.已知在锐角中,内角A,B,C的对边分别为a,b,c,,则的取值范围是( )
A. B. C. D.
二、多选题
9.在△ABC中,内角A,B,C的对边分别为a,b,c,则( )
A.若2cos C(acos B+bcos A)=c,则C=
B.若2cos C(acos B+bcos A)=c,则C=
C.若边BC的高为a,则当取得最大值时,A=
D.若边BC的高为a,则当取得最大值时,A=
10.已知分别是三个内角的对边,下列四个命题中正确的是( )
A.若是锐角三角形,则
B.若,则是等腰三角形
C.若,则是等腰三角形
D.若是等边三角形,则
11.在中,角、、的对边分别是,,且.若,有下列说法:①;②的取值可以为;③的面积没有最小值;④的面积的最大值为,其中正确说法为( )
A.① B.② C.③ D.④
12.在△ABC中,角,,的对边分别为,,,则下列结论中正确的是( )
A.在锐角三角形中,不等式恒成立
B.若则△ABC为锐角三角形
C.若acosB=bcosA+c,则△ABC一定是直角三角形
D.若,则△ABC一定是锐角三角形
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.如图,在单位圆中,, 分别在单位圆的第一 二象限内运动,若,为等边三角形,则___________.
14.中,内角,,的对边分别为,,,若面积为,,且,则________.
15.在中,,,,则__________.
16.在中,∠A=60°,AB=1,AC=2,则BC=___________.
四、解答题
17.在①;②;③,这三个条件中任选一个,补充在下面问题中.若问题中的三角形存在,求该三角形的周长;若问题中的三角形不存在,请说明理由.设的内角A,B,C的对边分别为a,b,c,且,,______.
18.如图,四边形内接于一个圆中,其中为直径,,,.
(1)求的长;
(2)求的面积.
19.的内角A,B,C的对边分别为a,b,c.已知.
(1)求B.
(2)___________,若问题中的三角形存在,试求出;若问题中的三角形不存在,请说明理由.
在①,②,③这三个条件中任选一个,补充在横线上.
注:如果选择多个条件分别解答,按第一个解答计分.
20.如图,为测量河对岸A,B两点的距离,在河的这边取C,D两点观察,测得,,,,(A,B,C,D在同一平面内),求A,B两点之间的距离.
21.如图,已知的半径为R,为其内接等边三角形,求的边长和的外接圆半径.
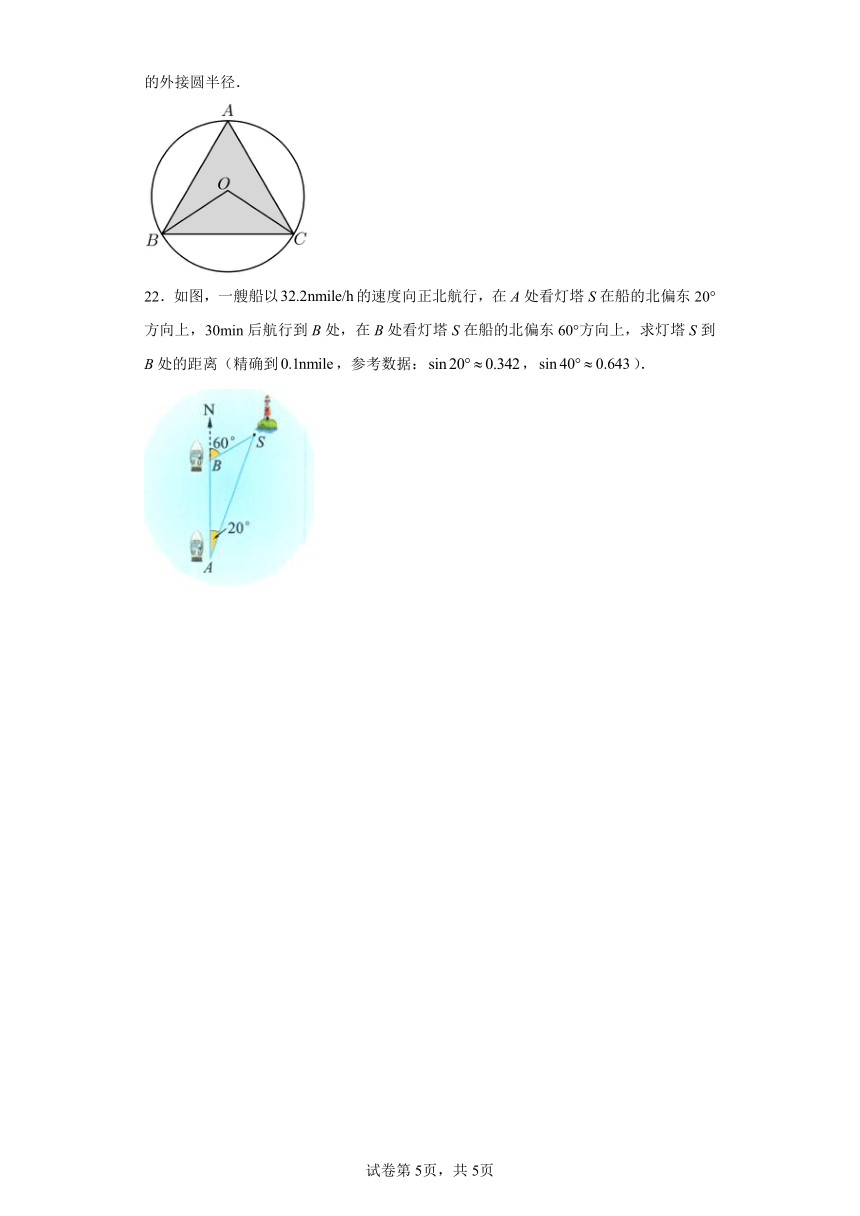
22.如图,一艘船以的速度向正北航行,在A处看灯塔S在船的北偏东20°方向上,30min后航行到B处,在B处看灯塔S在船的北偏东60°方向上,求灯塔S到B处的距离(精确到,参考数据:,).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
计算得到,,在中利用余弦定理计算得到答案.
【详解】
设塔高的高度为,在中,因为,所以;
在中,因为,所以;
在中,,,,
根据余弦定理可得,,
即,解得或(舍去).
故选:B.
2.A
【解析】
【分析】
先根据求出关系,代入面积公式,利用二次函数的知识求解最值.
【详解】
因为,所以,
即;
由正弦定理可得,所以
;
当时,取到最大值.
故选:A.
3.B
【解析】
【分析】
结合余弦定理求得正确答案.
【详解】
由,得,
由于,所以.
故选:B
4.A
【解析】
【分析】
根据给定信息作出图形,在直角三角形中直接计算作答.
【详解】
如图,依题意,,,,
于是得,,在中,,
所以塔的高度约为.
故选:A
5.B
【解析】
【分析】
由条件可得,由正弦定理结合三角形中有,利用正弦的和角公式可得,从而可得出答案.
【详解】
由,可得,所以,
所以.
在中,,故,
因为,所以,因为,所以,
故为直角三角形.
故选:B
6.C
【解析】
【分析】
根据已知条件结合正弦定理边化角可得,结合和余弦定理可得cosA和,根据三角形面积公式可得面积.
【详解】
∵,
结合正弦定理可得,
可得,∵,
结合余弦定理,可得,
∴A为锐角,且,从而求得,
∴的面积为.
故选:C.
7.B
【解析】
【分析】
根据给定条件可得,再利用正弦定理角化边,借助余弦定理计算判断作答.
【详解】
因的三个内角,而,则,
又,由正弦定理得:,
由余弦定理得:,整理得,即,是等腰三角形,
所以是等边三角形.
故选:B
8.D
【解析】
【分析】
由正弦定理把,表示为的函数,然后利用二倍角公式,两角和与差的余弦公式变形,并结合余弦函数性质得范围.
【详解】
由正弦定理得,则,,又,则,
所以
,
,所以,所以,
所以.
故选:D.
9.AC
【解析】
【分析】
根据正弦正理、三角形面积公式,结合余弦定理和辅助角公式进行判断即可.
【详解】
因为在△ABC中,0即2cos C·sin C=sin C,又sin C≠0,所以cos C=,所以C=,故A正确,B错误.
对于C,D,由等面积法得×a2=bcsin A,所以a2=2bcsin A,
又b2+c2=a2+2bccos A=2bcsin A+2bc·cos A,
则=2sin A+2cos A=4sin≤4,当且仅当A+=+2kπ,k∈Z,即A=+2kπ,k∈Z时,取得最大值4,又0故选:AC
10.ACD
【解析】
【分析】
利用诱导公式及正弦函数的性质可判断A,由正弦定理化边为角结合正弦的二倍角公式可判断B,由正弦定理化边为角,逆用两角和的正弦公式可判断C,利用正弦定理化边为角结合同角三角函数基本关系可判断D.
【详解】
对于A,因为是锐角三角形,所以,所以,即,故A正确;
对于B,由及正弦定理,可得,即,所以或,所以或,所以是等腰三角形或直角三角形,故B错误;
对于C,由及正弦定理化边为角,可知,即,因为为的内角,所以,所以是等腰三角形,故C正确;
对于D,由是等边三角形,所以,所以,由正弦定理,故D正确.
故选:ACD.
11.BCD
【解析】
【分析】
根据已知条件结合可得可判断①;由可判断②;由余弦定理结合基本不等式求出的范围,再由三角形的面积公式计算面积可判断③④,进而可得正确选项.
【详解】
由,得,即,
因为,所以,即,又因为,所以,故①不正确;
因为,所以,故的取值可以为,故②正确;
由余弦定理可得,
所以,所以,
即面积的最大值是,无最小值.故③,④正确;
故选:BCD.
12.ABC
【解析】
【分析】
直接利用三角函数关系式的变换,正弦定理余弦定理和三角形面积公式的应用进一步判定结果.
【详解】
解:对于A:若为锐角三角形,则为锐角,所以,由余弦定理,所以,故A正确;
对于B:假设为钝角三角形,不妨设,则,
,与题设矛盾.
又不是直角三角形,直角没有正切值,为锐角三角形,故B正确.
对于C,由余弦定理知,,化简整理得,为直角三角形,故C正确;
对于D:因为,所以,即,故,则由余弦定理可得,整理得,则是直角三角形,故D错误;
故选:ABC
13.##
【解析】
【分析】
先根据三角形面积公式求出,然后结合两角和与差的正弦公式求得答案.
【详解】
由题意,,而点N在第二象限,所以,因为,所以.
故答案为:.
14.
【解析】
【分析】
先由三角形的面积求出,再由余弦定理可求出结果
【详解】
由,得,
所以.
从而.
故答案为:
15.
【解析】
【分析】
由已知在中利用余弦定理可得的值,可求,可得,即可得解的值.
【详解】
解:因为在中,,,,
所以由余弦定理可得,
所以,即,
则.
故答案为:.
16.
【解析】
【分析】
根据给定条件利用余弦定理计算作答.
【详解】
在中,,AB=1,AC=2,由余弦定理得:
,则,
所以.
故答案为:
17.答案见解析.
【解析】
【分析】
根据可求B的大小.
若选①:根据正弦定理角化边,由得,根据余弦定理可求a和c;
若选②:根据余弦定理角化边,由可得a和B的关系,再结合余弦定理可求a和c;
若选③:由可求c,再根据余弦定理可求a.
【详解】
在中,,
∴,
∵,∴,
化简得,在中,,∴,
又∵,∴,
又∵,∴,即,
若选①,
∵,即,
又,∴,,
故此时存在,其周长为;
若选②,
∵,∴,
即,
又,∴,
故此时存在,其周长为;
若选③,
∵,∴,
又∵,∴,
该方程无解,∴三角形不存在.
18.(1);
(2).
【解析】
【分析】
(1)利用余弦定理可求得,利用正弦定理可求得结果;
(2)利用勾股定理可求得,利用三角形面积公式可得结果.
(1)
在中,由余弦定理得:
,解得:,
设为外接圆半径,由正弦定理得:,
即.
(2)
为直径,,
,,又,
.
19.(1)
(2)答案见解析
【解析】
【分析】
(1)由正弦定理及正弦的两角和公式可求解;
(2)选择条件①,由正弦定理及辅助角公式可求解;选择条件②,由余弦定理及正切三角函数可求解;选择条件③,由余弦定理可求解.
(1)
由,可得,则.
∴,
在中,,
则,∵,∴,∴,∵,∴.
(2)
选择条件①
,在中,,可得,
∵,∴,
∴,
根据辅助角公式,可得,
∵,∴,即,
故.
选择条件②
由,得,
∵,∴,因此,,
整理得,即,则.
在中,,∴.
故.
选择条件③
由,得,
即,
整理得,
由于,则方程无解,故不存在这样的三角形.
20.km
【解析】
【分析】
由题意,先计算得,,,由正弦定理计算,再由余弦定理计算
【详解】
∠DAC=180°﹣∠ADC﹣∠DCB﹣∠ACB=30°,∠DBC=180°﹣∠DCB﹣∠ADC﹣∠ADB=60°
在△ADC中由正弦定理得:
∴
在△CDB中由正弦定理得:
∴
在△ADB中由余弦定理得:AB2=DB2+AD2﹣2DB×ABcos∠ADB=2+9﹣2××3×=5
∴AB=km
答:A、B两点间的距离为km
21.的边长为,的外接圆半径为.
【解析】
【分析】
运用正弦定理,结合圆的性质进行求解即可.
【详解】
设等边三角形的边长为,的外接圆半径为,
由正弦定理可知:;
在中,由圆的性质可知:,
由正弦定理可知:,
所以的边长为,的外接圆半径为.
22.
【解析】
【分析】
根据题意,计算得的值,根据正弦定理计算.
【详解】
在中,,,,由正弦定理得,,即,所以灯塔S到B处的距离为
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,某市人民广场正中央有一座铁塔,为了测量塔高AB,某人先在塔的正西方点C处测得塔项的仰角为45°,然后从点C处沿南偏东30°方向前进60到达点D处,在D处测得塔项的仰角为,则铁塔AB的高度是( )
A.50 B.30 C.25 D.15
2.我国南宋时期著名的数学家秦九韶在其著作《数书九章》中独立提出了一种求三角形面积的方法“三斜求积术”,即的面积,其中分别为的内角的对边,若,且,则的面积的最大值为( )
A. B. C. D.
3.在中,若,则∠C=( ).
A.60° B.120° C.135° D.150°
4.东寺塔和西寺塔为昆明市城中古景,分别位于昆明市南面的书林街和东寺街,一东一西隔街相望,距今已有1100多年历史,在二月的梅花和烟雨中,“双塔烟雨”成为明清时的“昆明八景”之一.东寺塔基座为正方形,塔身有13级,塔顶四角立有四只铜皮做成的鸟,俗称金鸡,所以也有“金鸡塔”之称.如图,从东到西的公路上有相距80(单位:)的两个观测点,在点测得塔在北偏东60°的点处,在点测得塔在北偏西30°,塔顶的仰角为45°,则塔的高度约为( )
A. B. C. D.
5.的内角A,B,C的对边分别为a,b,c,若,则为( )
A.等腰非等边三角形 B.直角三角形
C.钝角三角形 D.等边三角形
6.的内角A,B,C的对边分别为a,b,c,已知,,则的面积为( )
A. B.
C. D.
7.设的三个内角满足,又,则这个三角形的形状是( )
A.直角三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
8.已知在锐角中,内角A,B,C的对边分别为a,b,c,,则的取值范围是( )
A. B. C. D.
二、多选题
9.在△ABC中,内角A,B,C的对边分别为a,b,c,则( )
A.若2cos C(acos B+bcos A)=c,则C=
B.若2cos C(acos B+bcos A)=c,则C=
C.若边BC的高为a,则当取得最大值时,A=
D.若边BC的高为a,则当取得最大值时,A=
10.已知分别是三个内角的对边,下列四个命题中正确的是( )
A.若是锐角三角形,则
B.若,则是等腰三角形
C.若,则是等腰三角形
D.若是等边三角形,则
11.在中,角、、的对边分别是,,且.若,有下列说法:①;②的取值可以为;③的面积没有最小值;④的面积的最大值为,其中正确说法为( )
A.① B.② C.③ D.④
12.在△ABC中,角,,的对边分别为,,,则下列结论中正确的是( )
A.在锐角三角形中,不等式恒成立
B.若则△ABC为锐角三角形
C.若acosB=bcosA+c,则△ABC一定是直角三角形
D.若,则△ABC一定是锐角三角形
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.如图,在单位圆中,, 分别在单位圆的第一 二象限内运动,若,为等边三角形,则___________.
14.中,内角,,的对边分别为,,,若面积为,,且,则________.
15.在中,,,,则__________.
16.在中,∠A=60°,AB=1,AC=2,则BC=___________.
四、解答题
17.在①;②;③,这三个条件中任选一个,补充在下面问题中.若问题中的三角形存在,求该三角形的周长;若问题中的三角形不存在,请说明理由.设的内角A,B,C的对边分别为a,b,c,且,,______.
18.如图,四边形内接于一个圆中,其中为直径,,,.
(1)求的长;
(2)求的面积.
19.的内角A,B,C的对边分别为a,b,c.已知.
(1)求B.
(2)___________,若问题中的三角形存在,试求出;若问题中的三角形不存在,请说明理由.
在①,②,③这三个条件中任选一个,补充在横线上.
注:如果选择多个条件分别解答,按第一个解答计分.
20.如图,为测量河对岸A,B两点的距离,在河的这边取C,D两点观察,测得,,,,(A,B,C,D在同一平面内),求A,B两点之间的距离.
21.如图,已知的半径为R,为其内接等边三角形,求的边长和的外接圆半径.
22.如图,一艘船以的速度向正北航行,在A处看灯塔S在船的北偏东20°方向上,30min后航行到B处,在B处看灯塔S在船的北偏东60°方向上,求灯塔S到B处的距离(精确到,参考数据:,).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
计算得到,,在中利用余弦定理计算得到答案.
【详解】
设塔高的高度为,在中,因为,所以;
在中,因为,所以;
在中,,,,
根据余弦定理可得,,
即,解得或(舍去).
故选:B.
2.A
【解析】
【分析】
先根据求出关系,代入面积公式,利用二次函数的知识求解最值.
【详解】
因为,所以,
即;
由正弦定理可得,所以
;
当时,取到最大值.
故选:A.
3.B
【解析】
【分析】
结合余弦定理求得正确答案.
【详解】
由,得,
由于,所以.
故选:B
4.A
【解析】
【分析】
根据给定信息作出图形,在直角三角形中直接计算作答.
【详解】
如图,依题意,,,,
于是得,,在中,,
所以塔的高度约为.
故选:A
5.B
【解析】
【分析】
由条件可得,由正弦定理结合三角形中有,利用正弦的和角公式可得,从而可得出答案.
【详解】
由,可得,所以,
所以.
在中,,故,
因为,所以,因为,所以,
故为直角三角形.
故选:B
6.C
【解析】
【分析】
根据已知条件结合正弦定理边化角可得,结合和余弦定理可得cosA和,根据三角形面积公式可得面积.
【详解】
∵,
结合正弦定理可得,
可得,∵,
结合余弦定理,可得,
∴A为锐角,且,从而求得,
∴的面积为.
故选:C.
7.B
【解析】
【分析】
根据给定条件可得,再利用正弦定理角化边,借助余弦定理计算判断作答.
【详解】
因的三个内角,而,则,
又,由正弦定理得:,
由余弦定理得:,整理得,即,是等腰三角形,
所以是等边三角形.
故选:B
8.D
【解析】
【分析】
由正弦定理把,表示为的函数,然后利用二倍角公式,两角和与差的余弦公式变形,并结合余弦函数性质得范围.
【详解】
由正弦定理得,则,,又,则,
所以
,
,所以,所以,
所以.
故选:D.
9.AC
【解析】
【分析】
根据正弦正理、三角形面积公式,结合余弦定理和辅助角公式进行判断即可.
【详解】
因为在△ABC中,0
对于C,D,由等面积法得×a2=bcsin A,所以a2=2bcsin A,
又b2+c2=a2+2bccos A=2bcsin A+2bc·cos A,
则=2sin A+2cos A=4sin≤4,当且仅当A+=+2kπ,k∈Z,即A=+2kπ,k∈Z时,取得最大值4,又0
10.ACD
【解析】
【分析】
利用诱导公式及正弦函数的性质可判断A,由正弦定理化边为角结合正弦的二倍角公式可判断B,由正弦定理化边为角,逆用两角和的正弦公式可判断C,利用正弦定理化边为角结合同角三角函数基本关系可判断D.
【详解】
对于A,因为是锐角三角形,所以,所以,即,故A正确;
对于B,由及正弦定理,可得,即,所以或,所以或,所以是等腰三角形或直角三角形,故B错误;
对于C,由及正弦定理化边为角,可知,即,因为为的内角,所以,所以是等腰三角形,故C正确;
对于D,由是等边三角形,所以,所以,由正弦定理,故D正确.
故选:ACD.
11.BCD
【解析】
【分析】
根据已知条件结合可得可判断①;由可判断②;由余弦定理结合基本不等式求出的范围,再由三角形的面积公式计算面积可判断③④,进而可得正确选项.
【详解】
由,得,即,
因为,所以,即,又因为,所以,故①不正确;
因为,所以,故的取值可以为,故②正确;
由余弦定理可得,
所以,所以,
即面积的最大值是,无最小值.故③,④正确;
故选:BCD.
12.ABC
【解析】
【分析】
直接利用三角函数关系式的变换,正弦定理余弦定理和三角形面积公式的应用进一步判定结果.
【详解】
解:对于A:若为锐角三角形,则为锐角,所以,由余弦定理,所以,故A正确;
对于B:假设为钝角三角形,不妨设,则,
,与题设矛盾.
又不是直角三角形,直角没有正切值,为锐角三角形,故B正确.
对于C,由余弦定理知,,化简整理得,为直角三角形,故C正确;
对于D:因为,所以,即,故,则由余弦定理可得,整理得,则是直角三角形,故D错误;
故选:ABC
13.##
【解析】
【分析】
先根据三角形面积公式求出,然后结合两角和与差的正弦公式求得答案.
【详解】
由题意,,而点N在第二象限,所以,因为,所以.
故答案为:.
14.
【解析】
【分析】
先由三角形的面积求出,再由余弦定理可求出结果
【详解】
由,得,
所以.
从而.
故答案为:
15.
【解析】
【分析】
由已知在中利用余弦定理可得的值,可求,可得,即可得解的值.
【详解】
解:因为在中,,,,
所以由余弦定理可得,
所以,即,
则.
故答案为:.
16.
【解析】
【分析】
根据给定条件利用余弦定理计算作答.
【详解】
在中,,AB=1,AC=2,由余弦定理得:
,则,
所以.
故答案为:
17.答案见解析.
【解析】
【分析】
根据可求B的大小.
若选①:根据正弦定理角化边,由得,根据余弦定理可求a和c;
若选②:根据余弦定理角化边,由可得a和B的关系,再结合余弦定理可求a和c;
若选③:由可求c,再根据余弦定理可求a.
【详解】
在中,,
∴,
∵,∴,
化简得,在中,,∴,
又∵,∴,
又∵,∴,即,
若选①,
∵,即,
又,∴,,
故此时存在,其周长为;
若选②,
∵,∴,
即,
又,∴,
故此时存在,其周长为;
若选③,
∵,∴,
又∵,∴,
该方程无解,∴三角形不存在.
18.(1);
(2).
【解析】
【分析】
(1)利用余弦定理可求得,利用正弦定理可求得结果;
(2)利用勾股定理可求得,利用三角形面积公式可得结果.
(1)
在中,由余弦定理得:
,解得:,
设为外接圆半径,由正弦定理得:,
即.
(2)
为直径,,
,,又,
.
19.(1)
(2)答案见解析
【解析】
【分析】
(1)由正弦定理及正弦的两角和公式可求解;
(2)选择条件①,由正弦定理及辅助角公式可求解;选择条件②,由余弦定理及正切三角函数可求解;选择条件③,由余弦定理可求解.
(1)
由,可得,则.
∴,
在中,,
则,∵,∴,∴,∵,∴.
(2)
选择条件①
,在中,,可得,
∵,∴,
∴,
根据辅助角公式,可得,
∵,∴,即,
故.
选择条件②
由,得,
∵,∴,因此,,
整理得,即,则.
在中,,∴.
故.
选择条件③
由,得,
即,
整理得,
由于,则方程无解,故不存在这样的三角形.
20.km
【解析】
【分析】
由题意,先计算得,,,由正弦定理计算,再由余弦定理计算
【详解】
∠DAC=180°﹣∠ADC﹣∠DCB﹣∠ACB=30°,∠DBC=180°﹣∠DCB﹣∠ADC﹣∠ADB=60°
在△ADC中由正弦定理得:
∴
在△CDB中由正弦定理得:
∴
在△ADB中由余弦定理得:AB2=DB2+AD2﹣2DB×ABcos∠ADB=2+9﹣2××3×=5
∴AB=km
答:A、B两点间的距离为km
21.的边长为,的外接圆半径为.
【解析】
【分析】
运用正弦定理,结合圆的性质进行求解即可.
【详解】
设等边三角形的边长为,的外接圆半径为,
由正弦定理可知:;
在中,由圆的性质可知:,
由正弦定理可知:,
所以的边长为,的外接圆半径为.
22.
【解析】
【分析】
根据题意,计算得的值,根据正弦定理计算.
【详解】
在中,,,,由正弦定理得,,即,所以灯塔S到B处的距离为
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
