高中数学同步指导试卷苏教版(2019)必修第二册统计1(word版含解析)
文档属性
| 名称 | 高中数学同步指导试卷苏教版(2019)必修第二册统计1(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 704.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 21:25:55 | ||
图片预览


文档简介
高中数学同步指导试卷苏教版(2019)必修第二册统计
一、单选题
1.要考察某公司生产的克袋装牛奶的质量是否达标,现从袋牛奶中抽取袋进行检验,将它们编号为、、、、,利用随机数表抽取样本,从第行第列的数开始,按位数依次向右读取,到行末后接着从下一行第一个数继续.则第三袋牛奶的标号是( )
(下面摘取了某随机数表的第行至第行)
A. B. C. D.
2.某大学数学系共有本科生1500人,其中一、二、三、四年级的人数比为,要用分层随机抽样的方法从中抽取一个容量为300的样本,则应抽取的三年级学生的人数为( )
A.20 B.40 C.60 D.80
3.有下列三个命题:
①分层抽样中,每个个体被抽到的可能性与层数及分层有关;
②散点图是判断两个变量是否相关的一种重要方法和手段;
③在频率分布直方图中,各小长方形的面积之和为1.
其中为真命题的是( )
A.①② B.①③ C.②③ D.①②③
4.已知数据的平均数为,方差为,中位数为,极差为.由这组数据得到新数据,其中,则下列命题中错误的是( )
A.新数据的平均数是 B.新数据的方差是
C.新数据的中位数是 D.新数据的极差是
5.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查有关消费购买力的某项指标;(2)从某中学高一年级的10名体育特长生中抽取3人调查学习情况;应采用的抽样方法分别是( )
A.(1)用简单随机抽样,(2)用分层随机抽样 B.(1)(2)都用简单随机抽样
C.(1)用分层随机抽样,(2)用简单随机抽样 D.(1)(2)都用分层随机抽样
6.立德中学高一年级共有学生640人,其中男生300人,现采用分层抽样的方法调查学生的身高情况,在抽取的样本中,男生有30人,那么该样本中女生的人数为( )
A.30人 B.34人 C.60人 D.64人
7.下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )A.2950 B.3050 C.3130 D.3000
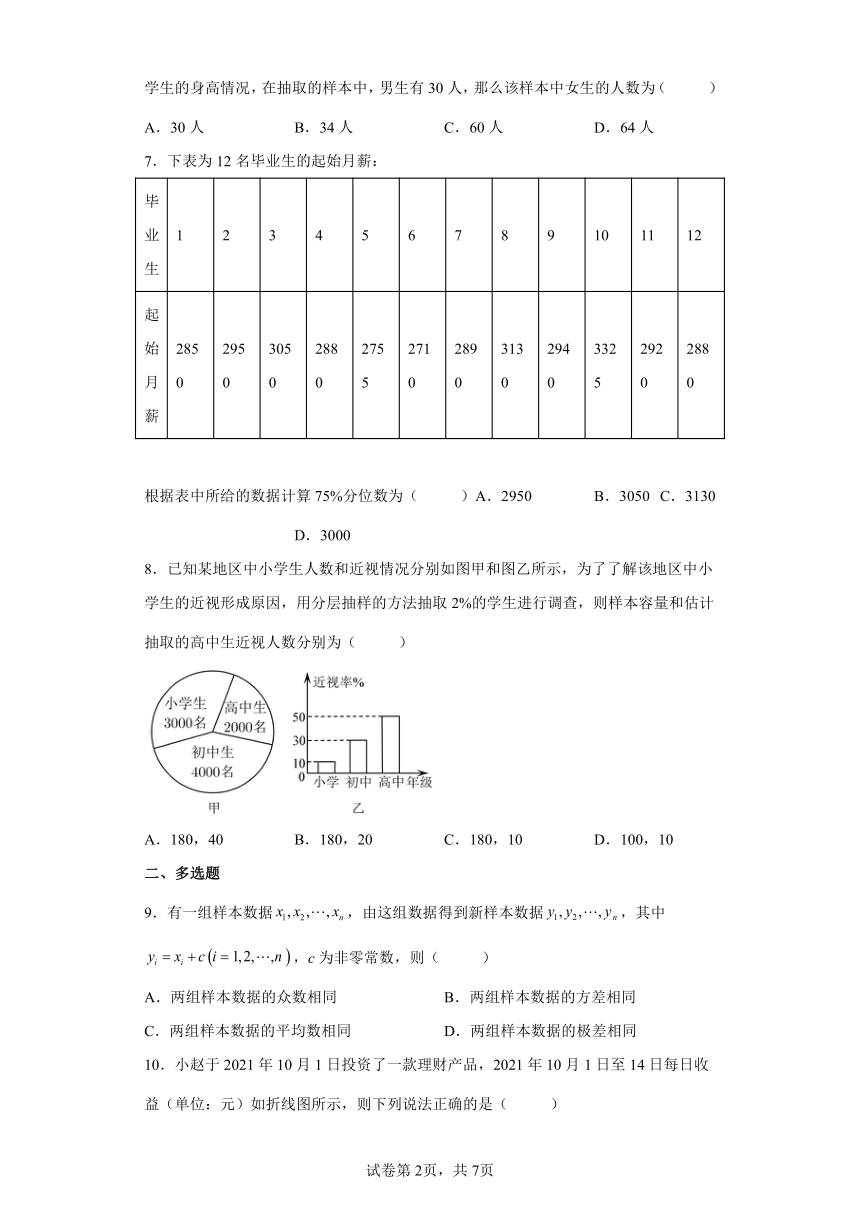
8.已知某地区中小学生人数和近视情况分别如图甲和图乙所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和估计抽取的高中生近视人数分别为( )
A.180,40 B.180,20 C.180,10 D.100,10
二、多选题
9.有一组样本数据,由这组数据得到新样本数据,其中,c为非零常数,则( )
A.两组样本数据的众数相同 B.两组样本数据的方差相同
C.两组样本数据的平均数相同 D.两组样本数据的极差相同
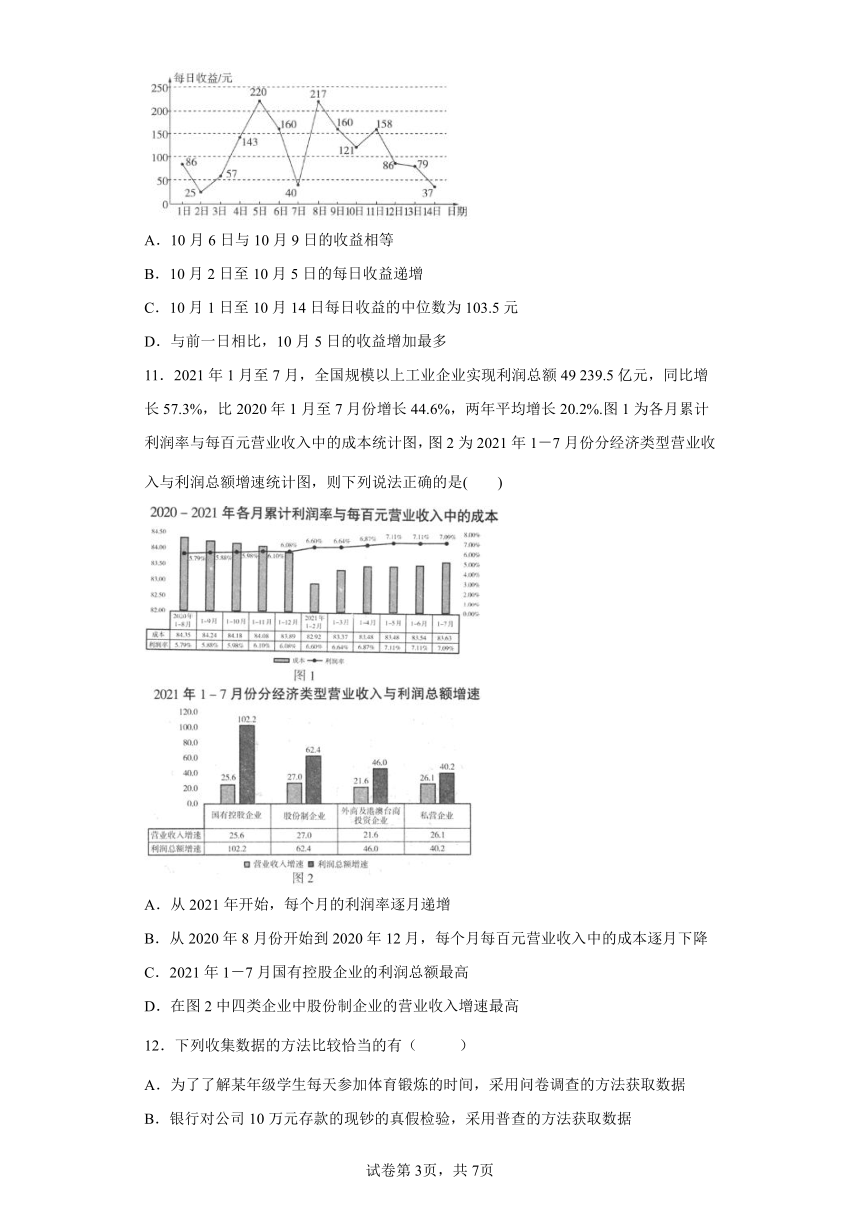
10.小赵于2021年10月1日投资了一款理财产品,2021年10月1日至14日每日收益(单位:元)如折线图所示,则下列说法正确的是( )
A.10月6日与10月9日的收益相等
B.10月2日至10月5日的每日收益递增
C.10月1日至10月14日每日收益的中位数为103.5元
D.与前一日相比,10月5日的收益增加最多
11.2021年1月至7月,全国规模以上工业企业实现利润总额49 239.5亿元,同比增长57.3%,比2020年1月至7月份增长44.6%,两年平均增长20.2%.图1为各月累计利润率与每百元营业收入中的成本统计图,图2为2021年1-7月份分经济类型营业收入与利润总额增速统计图,则下列说法正确的是( )
A.从2021年开始,每个月的利润率逐月递增
B.从2020年8月份开始到2020年12月,每个月每百元营业收入中的成本逐月下降
C.2021年1-7月国有控股企业的利润总额最高
D.在图2中四类企业中股份制企业的营业收入增速最高
12.下列收集数据的方法比较恰当的有( )
A.为了了解某年级学生每天参加体育锻炼的时间,采用问卷调查的方法获取数据
B.银行对公司10万元存款的现钞的真假检验,采用普查的方法获取数据
C.检验一批汽车的防碰撞性能,采用抽样调查的方法获取数据
D.某医药公司欲研制一种新型病毒的特效药,通过试验获取数据
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.某车间生产A,B,C三种不同型号的产品,产量之比分别为5:k:3,为检验产品的质量,现用分层抽样的方法抽取一个容量为120的样本进行检验,已知B种型号的产品共抽取了24件,则C种型号的产品抽取的件数为_________.
14.某班学号的学生铅球测试成绩如下表:
学号 1 2 3 4 5 6 7 8
成绩 9.1 7.9 8.4 6.9 5.2 7.1 8.0 8.1
可以估计这8名学生铅球测试成绩的第25百分位数为___________.
15.某次高一年级数学期末考试的填空题第六题,答对得4分,答错得0分,全年级480人的正确率高达90%,则全年级该题得分的标准差为___________.
16.某人6次上班途中所花的时间(单位:分钟)分别为9、8、、12、15、12,已知这组数据的平均数为11,则中位数是___________.
四、解答题
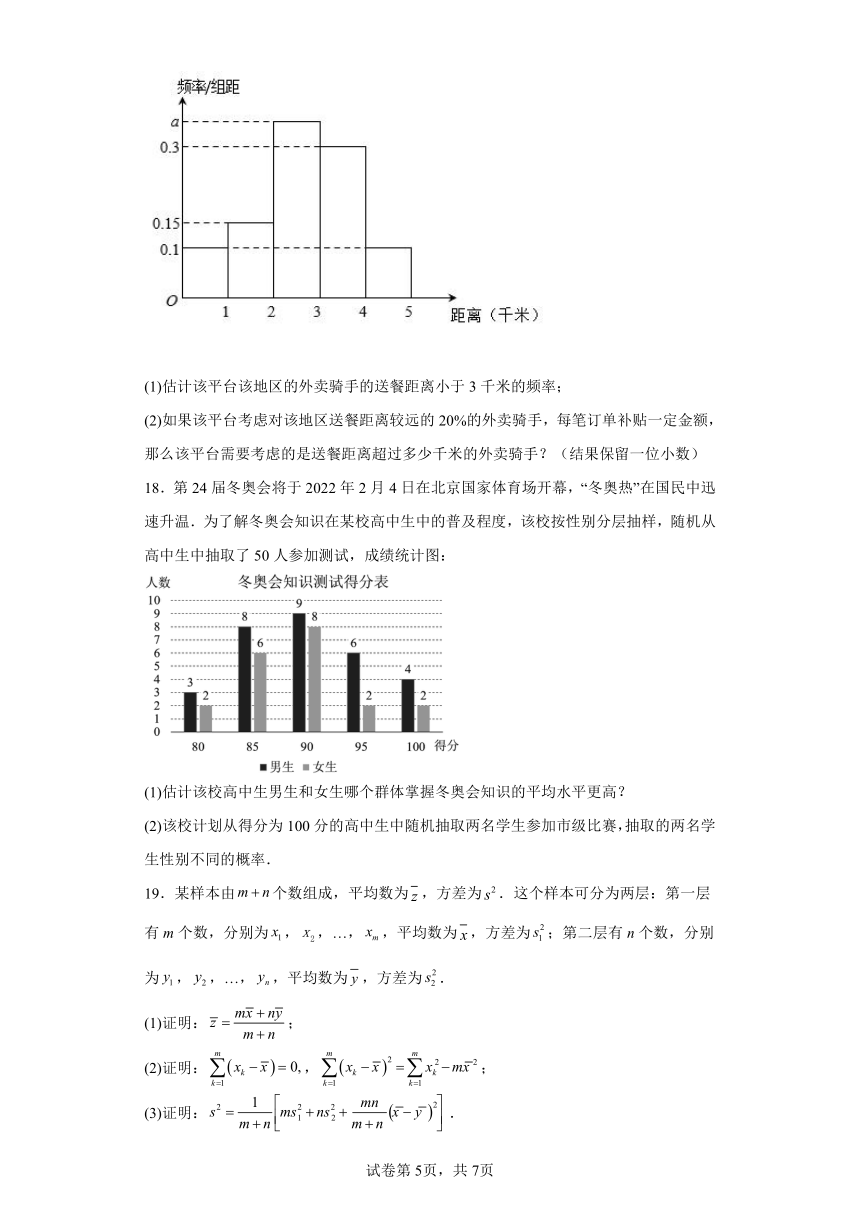
17.截至2021年6月,我国网上外卖用户规模达4.69亿.与此同时,外卖行业与骑手权益保障也受到社会广泛关注,行业生态环境持续改善,推动外卖行业健康长远发展.某外卖平台为了优化某地区的外卖配送系统,从该平台在该地区已完成的订单中随机抽取200个订单,统计外卖骑手的送餐距离(单位:千米).将所得数据按照,,,,分成5组,得到的频率分布直方图如图所示.
(1)估计该平台该地区的外卖骑手的送餐距离小于3千米的频率;
(2)如果该平台考虑对该地区送餐距离较远的20%的外卖骑手,每笔订单补贴一定金额,那么该平台需要考虑的是送餐距离超过多少千米的外卖骑手?(结果保留一位小数)
18.第24届冬奥会将于2022年2月4日在北京国家体育场开幕,“冬奥热”在国民中迅速升温.为了解冬奥会知识在某校高中生中的普及程度,该校按性别分层抽样,随机从高中生中抽取了50人参加测试,成绩统计图:
(1)估计该校高中生男生和女生哪个群体掌握冬奥会知识的平均水平更高?
(2)该校计划从得分为100分的高中生中随机抽取两名学生参加市级比赛,抽取的两名学生性别不同的概率.
19.某样本由个数组成,平均数为,方差为.这个样本可分为两层:第一层有m个数,分别为,,…,,平均数为,方差为;第二层有n个数,分别为,,…,,平均数为,方差为.
(1)证明:;
(2)证明:,;
(3)证明:.
20.某校高三年级甲班50名学生在一次期中考试中,数学成绩的频率分布直方图如图所示,成绩分组区间为,,,,,,.其中a,b,c成等差数列,且.物理成绩统计如表所示.(说明:数学成绩满分为150分,物理成绩满分为100分)
物理成绩频数分布表:
分组
频数 6 9 20 10 5
(1)根据甲班数学成绩的频率分布直方图,估计甲班数学成绩的平均分;
(2)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知甲班中数学或物理成绩中至少有一科为“优”的学生总共有6人,从这6人中随机抽取3人,记X表示抽到数学和物理两科成绩都是“优”的学生人数,求X的分布列及期望.
21.甲乙两个班参加了同一学科的考试,其中甲班40人,乙班30人,乙班的平均成绩70分,方差为130,甲班按分数段按相应的比例随机抽取了10名同学的成绩如下:56,66,68,72,77,79,82,86,91,93.
(1)计算甲班这10名同学成绩的平均数和方差;
(2)用甲班这10名同学的平均数和方差估计甲班全体同学的平均数和方差,那么甲、乙两班全部70名同学的平均成绩和方差分别为多少?
22.某食品公司为了调查消费者对某款新食品的认可情况,随机抽取了100位消费者进行食品认可度(共设,,,四个等级)的调查,每位被调查的消费者均对该食品认可度等级进行了评定,调查的结果如下图(表):
男性消费者
认可度等级 频数 频率
级 18 0.3
级 24 0.4
级
级
(1)求,,的值,并求被调查者中,认可度等级为级的女性消费者人数;
(2)公司计划按性别采用分层抽样的方法从认可度等级为级或级的消费者中选取11人派送礼品,分别求被选中的男性消费者人数和女性消费者人数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
利用随机数表法可得结果.
【详解】
由随机数表法可知,前三袋牛奶的标号依次为、、,故第三袋牛奶的标号是.
故选:B.
2.C
【解析】
【分析】
根据给定条件利用分层抽样的抽样比直接计算作答.
【详解】
依题意,三年级学生的总人数为,
从1500人中用分层随机抽样抽取容量为300的样本的抽样比为,
所以应抽取的三年级学生的人数为.
故选:C
3.C
【解析】
【分析】
根据分层抽样的性质、散点图的定义、频率分布直方图的特点依次判断命题即可.
【详解】
由分层抽样的性质可得,每个个体被被抽到的可能性与层数及分层无关,故命题①为假;
由散点图的定义可知,它是判断两个变量是否相关的一种重要方法和手段,故命题②为真;
在频率分布直方图中,每个小矩形的面积为该组的频率,又频率之和为1,所以各小长方形的面积之和为1,故命题③真.
故选:C
4.C
【解析】
【分析】
根据平均数、方差、中位数、极差的定义求解.
【详解】
解:对于选项A:因为,所以新数据的平均数为,故选项A正确,
对于选项B:因为,所以新数据的方差为,故选项B正确,
对于选项C:因为数据,,,的中位数为,所以新数据的中位数是,故选项C错误,
对于选项D:设数据,,,中最大,最小(其中,,,,则,所以新数据的极差是,故选项D正确,
故选:C.
5.C
【解析】
【分析】
根据简单随机抽样、分层抽样的适用条件进行分析判断.
【详解】
因为有关消费购买力的某项指标受家庭收入的影响,而社区家庭收入差距明显,所以①用分层抽样;
从10名体育特长生中抽取3人调查学习情况,个体之间差别不大,且总体和样本容量较小,所以②用简单随机抽样.
故选:C
6.B
【解析】
【分析】
根据直接求解.
【详解】
得
故选:B
7.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
8.B
【解析】
【分析】
利用总量乘以抽取比例即可得到样本容量;根据图表可知高中生近视率 从而估计抽取的高中生近视人数
【详解】
所有学生数为3000+4000+2000=9000,故样本容量为 9000×2%=180,
根据图甲以及抽取百分比可知,样本中高中生人数为2000×2%=40,
根据图乙可知,抽取的高中生近视人数为40×50%=20,
故选:B.
9.BD
【解析】
【分析】
根据众数、方差、平均数和极差的定义,算出对应数字特征即可判断答案.
【详解】
对A,设样本数据的众数为,则新样本数据的众数为,则A错误;
对B,样本数据的方差为,新样本数据的方差为,B正确;
对C,原数据的平均数,新数据的平均数,则C错误;
对D,不妨设样本数据中分别为最小值和最大值,极差为,则新样本数据中分别最小和最大,则极差,D正确.
故选:BD.
10.ABC
【解析】
【分析】
根据折线图上的数据可直接得到AB是正确的,10月1日至10月14日每日收益的中位数为故C也正确,10月8日和前一日比较收益增加最多,故D错误.
【详解】
由题中折线图可知,10月6日与10月9日的收益均为160元,故A正确;
由题中折线图可以看出,10月2日至10月5日的每日收益递增,故B正确;
10月1日至10月14日每日收益的中位数为(元),故C正确;
10月8日比前一日收益增加(元),
而10月5日比前一日收益增加(元),
10月8日和前一日比较收益增加177元,故D错误.
故选:ABC.
11.BD
【解析】
【分析】
A:根据图1中2021年1—2月的数据和5月到6月的利润率增速即可判断;
B:根据图1的2020年8月到2020年12月的每百元营业收入中的成本数据即可判断;
C:根据图2可以判断增速,但无法判断利润额的大小;
D:根据图2中营业收入增速数据即可判断.
【详解】
对于选项A,2021年1—2月的数据在一起,看不出是否增长,且从5月到6月增速相同,也没有递增,故选项A错误;
根据图1的信息即可判断B选项正确;
对于选项C,通过图2可知,国有控股企业的利润总额增速最大,利润总额是否最高不能确定,故选项C错误;
在图2中股份制企业的营业收入增速为27.0,确实是四类企业中最高值,故选项D正确.
故选:BD.
12.ABCD
【解析】
【分析】
根据收集数据的几种方法即可得出答案.
【详解】
收集数据主要有普查和抽样调查,
除此还有问卷调查﹑持续观察﹑做调查、查阅资料、做试验等;
接下来根据人数的多少以及调查的目的进行选择.
故选:ABCD
13.36
【解析】
【分析】
根据题意可得,解方程求出的值,再根据种型号的产品所占的比例,求出种型号的产品应抽取的数量.
【详解】
由题意,得,所以k=2,
所以C种型号的产品抽取的件数为12036.
故答案为:36.
14.
【解析】
【分析】
利用百分位数的计算方法即可求解.
【详解】
将以上数据从小到大排列为,,,,,,,;
%,则第25百分位数第项和第项的平均数,即为.
故答案为:.
15.##
【解析】
【分析】
根据平均数、方差公式计算可得;
【详解】
解:依题意全年级答对的有人,答错的有人,所以全年级的平均分为,所以方差为,则标准差为;
故答案为:
16.11
【解析】
【分析】
直接根据平均数的公式和中位数的定义计算得到答案.
【详解】
,解得.
数据从小到大排列得到:,中位数为.
故答案为:11.
17.(1)0.6
(2)3.7千米
【解析】
【分析】
(1)首先由频率分布直方图求出,求出后两组频率之和即得;
(2)设送餐距离较远的20%的外卖骑手对应的距离为,即距离不小于的频率为0.2,由最后一组的频率与后两组频率和可得,然后计算可得可得.
(1)
由,解得.
所以该平台该地区的外卖骑手的送餐距离小于3千米的频率为.
(2)
由频率分布直方图可得,最后1组的频率为0.1,
后2组的频率之和为.
设送餐距离较远的20%的外卖骑手对应的距离为千米,则.
所以,解得.
故该平台需要考虑的是送餐距离超过3.7千米的外卖骑手.
18.(1)该校高中生男生群体掌握冬奥会知识的平均水平高于女生
(2)
【解析】
【分析】
(1)先求出男生和女生的平均分、,比较两个数的大小即可;
(2)设男生中满分学生分别为,,,,女生满分学生分别为A,,利用列举法列出所有可能的结果和性别不同的结果,进而得出答案.
(1)
设男生和女生的平均得分分别为、,则
,
.
∵,∴该校高中生男生群体掌握冬奥会知识的平均水平高于女生.
(2)
由统计图可知,得分为100分的人数为6人,
设男生中满分学生分别为,,,,女生满分学生分别为A,,共6人,现从6人中随机抽取两人,共有如下15种可能:
,,,,,
,,,,
,,,
,,
,
其中性别不同的有如下8种可能:
,;,;,;,.
∴抽取的两名学生性别不同的概率为.
19.(1)证明见解析;
(2)证明见解析;
(3)证明见解析.
【解析】
【分析】
(1)利用平均数的定义及计算公式即证;
(2)利用平均数的含义及计算公式即证;
(3)利用平均数、方差的定义及计算公式即证;
(1)
根据平均数定义,,
故,
因此.
(2)
因为,,
所以.
因为,,
所以
.
(3)
方法一:由方差定义可得,由(2)可知,
所以
.
同理,于是
将代入化简得.
方法二:由题设,所以
.
同理,于是
将代入化简得.
20.(1)分;
(2)分布列见解析,期望为.
【解析】
【分析】
(1)根据题意,结合频率分布直方图的性质,求得,再利用平均数的计算公式,即可求解;
(2)根据题意得到6人中有人数学和物理两科都为“优秀”,得出的可能取值为,求得相应的概率,得出分布列,利用期望的公式,即可求解.
(1)
解:因为a,b,c成等差数列,且,所以,可得,
由频率分布直方图,可得,
所以,解得,所以,
所以估计甲班数学成绩的平均分为:
(分).
(2)
解:甲班中物理成绩为优秀的有5人,数学成绩为优秀的有人,
因为数学或物理成绩至少有一科为“优秀”的学生共有6人,
所以6人中有人数学和物理两科都为“优秀”,
从这6人中随机抽取3人,记表示抽到数学和入了两科成绩都是“优秀”的学生人数,则随机变量的可能取值为,
则,
,
所以的分布列为:
所以期望为.
21.(1)77;123
(2)74;138
【解析】
【分析】
(1)直接代公式求出平均数和方差;
(2)记这70名同学的平均成绩和方差分别为,,根据分层抽样中两组数据x,y的抽样比例求平均数和方差.
(1)
,
;
(2)
记这70名同学的平均成绩和方差分别为,,
分层抽样中两组数据x,y的抽样比例是,则总体均值为,
所以,,
总体方差,
.
22.(1);;;认可度等级为级的女性消费者人数为14;
(2)被选中的男性消费者人数为7,女性消费者人数为4.
【解析】
【分析】
(1)利用频率的概念及性质可求,,的值,进而可得女性消费者人数,再结合条件即得;
(2)由题可得认可度等级为级或级的男性消费者及女性消费者人数,再利用分层抽样的概念即求.
(1)
由表可知,,即.
由题可得男性消费者人数为,
所以,,
被调查者中,女性消费者人数为,
故认可度等级为级的女性消费者人数为.
所以,,,认可度等级为级的女性消费者人数为14;
(2)
由题可知认可度等级为级或级的男性消费者有人,认可度等级为级或级的女性消费者有人,
从中选取11人,则被选中的男性消费者人数为,女性消费者人数为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.要考察某公司生产的克袋装牛奶的质量是否达标,现从袋牛奶中抽取袋进行检验,将它们编号为、、、、,利用随机数表抽取样本,从第行第列的数开始,按位数依次向右读取,到行末后接着从下一行第一个数继续.则第三袋牛奶的标号是( )
(下面摘取了某随机数表的第行至第行)
A. B. C. D.
2.某大学数学系共有本科生1500人,其中一、二、三、四年级的人数比为,要用分层随机抽样的方法从中抽取一个容量为300的样本,则应抽取的三年级学生的人数为( )
A.20 B.40 C.60 D.80
3.有下列三个命题:
①分层抽样中,每个个体被抽到的可能性与层数及分层有关;
②散点图是判断两个变量是否相关的一种重要方法和手段;
③在频率分布直方图中,各小长方形的面积之和为1.
其中为真命题的是( )
A.①② B.①③ C.②③ D.①②③
4.已知数据的平均数为,方差为,中位数为,极差为.由这组数据得到新数据,其中,则下列命题中错误的是( )
A.新数据的平均数是 B.新数据的方差是
C.新数据的中位数是 D.新数据的极差是
5.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查有关消费购买力的某项指标;(2)从某中学高一年级的10名体育特长生中抽取3人调查学习情况;应采用的抽样方法分别是( )
A.(1)用简单随机抽样,(2)用分层随机抽样 B.(1)(2)都用简单随机抽样
C.(1)用分层随机抽样,(2)用简单随机抽样 D.(1)(2)都用分层随机抽样
6.立德中学高一年级共有学生640人,其中男生300人,现采用分层抽样的方法调查学生的身高情况,在抽取的样本中,男生有30人,那么该样本中女生的人数为( )
A.30人 B.34人 C.60人 D.64人
7.下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )A.2950 B.3050 C.3130 D.3000
8.已知某地区中小学生人数和近视情况分别如图甲和图乙所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和估计抽取的高中生近视人数分别为( )
A.180,40 B.180,20 C.180,10 D.100,10
二、多选题
9.有一组样本数据,由这组数据得到新样本数据,其中,c为非零常数,则( )
A.两组样本数据的众数相同 B.两组样本数据的方差相同
C.两组样本数据的平均数相同 D.两组样本数据的极差相同
10.小赵于2021年10月1日投资了一款理财产品,2021年10月1日至14日每日收益(单位:元)如折线图所示,则下列说法正确的是( )
A.10月6日与10月9日的收益相等
B.10月2日至10月5日的每日收益递增
C.10月1日至10月14日每日收益的中位数为103.5元
D.与前一日相比,10月5日的收益增加最多
11.2021年1月至7月,全国规模以上工业企业实现利润总额49 239.5亿元,同比增长57.3%,比2020年1月至7月份增长44.6%,两年平均增长20.2%.图1为各月累计利润率与每百元营业收入中的成本统计图,图2为2021年1-7月份分经济类型营业收入与利润总额增速统计图,则下列说法正确的是( )
A.从2021年开始,每个月的利润率逐月递增
B.从2020年8月份开始到2020年12月,每个月每百元营业收入中的成本逐月下降
C.2021年1-7月国有控股企业的利润总额最高
D.在图2中四类企业中股份制企业的营业收入增速最高
12.下列收集数据的方法比较恰当的有( )
A.为了了解某年级学生每天参加体育锻炼的时间,采用问卷调查的方法获取数据
B.银行对公司10万元存款的现钞的真假检验,采用普查的方法获取数据
C.检验一批汽车的防碰撞性能,采用抽样调查的方法获取数据
D.某医药公司欲研制一种新型病毒的特效药,通过试验获取数据
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.某车间生产A,B,C三种不同型号的产品,产量之比分别为5:k:3,为检验产品的质量,现用分层抽样的方法抽取一个容量为120的样本进行检验,已知B种型号的产品共抽取了24件,则C种型号的产品抽取的件数为_________.
14.某班学号的学生铅球测试成绩如下表:
学号 1 2 3 4 5 6 7 8
成绩 9.1 7.9 8.4 6.9 5.2 7.1 8.0 8.1
可以估计这8名学生铅球测试成绩的第25百分位数为___________.
15.某次高一年级数学期末考试的填空题第六题,答对得4分,答错得0分,全年级480人的正确率高达90%,则全年级该题得分的标准差为___________.
16.某人6次上班途中所花的时间(单位:分钟)分别为9、8、、12、15、12,已知这组数据的平均数为11,则中位数是___________.
四、解答题
17.截至2021年6月,我国网上外卖用户规模达4.69亿.与此同时,外卖行业与骑手权益保障也受到社会广泛关注,行业生态环境持续改善,推动外卖行业健康长远发展.某外卖平台为了优化某地区的外卖配送系统,从该平台在该地区已完成的订单中随机抽取200个订单,统计外卖骑手的送餐距离(单位:千米).将所得数据按照,,,,分成5组,得到的频率分布直方图如图所示.
(1)估计该平台该地区的外卖骑手的送餐距离小于3千米的频率;
(2)如果该平台考虑对该地区送餐距离较远的20%的外卖骑手,每笔订单补贴一定金额,那么该平台需要考虑的是送餐距离超过多少千米的外卖骑手?(结果保留一位小数)
18.第24届冬奥会将于2022年2月4日在北京国家体育场开幕,“冬奥热”在国民中迅速升温.为了解冬奥会知识在某校高中生中的普及程度,该校按性别分层抽样,随机从高中生中抽取了50人参加测试,成绩统计图:
(1)估计该校高中生男生和女生哪个群体掌握冬奥会知识的平均水平更高?
(2)该校计划从得分为100分的高中生中随机抽取两名学生参加市级比赛,抽取的两名学生性别不同的概率.
19.某样本由个数组成,平均数为,方差为.这个样本可分为两层:第一层有m个数,分别为,,…,,平均数为,方差为;第二层有n个数,分别为,,…,,平均数为,方差为.
(1)证明:;
(2)证明:,;
(3)证明:.
20.某校高三年级甲班50名学生在一次期中考试中,数学成绩的频率分布直方图如图所示,成绩分组区间为,,,,,,.其中a,b,c成等差数列,且.物理成绩统计如表所示.(说明:数学成绩满分为150分,物理成绩满分为100分)
物理成绩频数分布表:
分组
频数 6 9 20 10 5
(1)根据甲班数学成绩的频率分布直方图,估计甲班数学成绩的平均分;
(2)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知甲班中数学或物理成绩中至少有一科为“优”的学生总共有6人,从这6人中随机抽取3人,记X表示抽到数学和物理两科成绩都是“优”的学生人数,求X的分布列及期望.
21.甲乙两个班参加了同一学科的考试,其中甲班40人,乙班30人,乙班的平均成绩70分,方差为130,甲班按分数段按相应的比例随机抽取了10名同学的成绩如下:56,66,68,72,77,79,82,86,91,93.
(1)计算甲班这10名同学成绩的平均数和方差;
(2)用甲班这10名同学的平均数和方差估计甲班全体同学的平均数和方差,那么甲、乙两班全部70名同学的平均成绩和方差分别为多少?
22.某食品公司为了调查消费者对某款新食品的认可情况,随机抽取了100位消费者进行食品认可度(共设,,,四个等级)的调查,每位被调查的消费者均对该食品认可度等级进行了评定,调查的结果如下图(表):
男性消费者
认可度等级 频数 频率
级 18 0.3
级 24 0.4
级
级
(1)求,,的值,并求被调查者中,认可度等级为级的女性消费者人数;
(2)公司计划按性别采用分层抽样的方法从认可度等级为级或级的消费者中选取11人派送礼品,分别求被选中的男性消费者人数和女性消费者人数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
利用随机数表法可得结果.
【详解】
由随机数表法可知,前三袋牛奶的标号依次为、、,故第三袋牛奶的标号是.
故选:B.
2.C
【解析】
【分析】
根据给定条件利用分层抽样的抽样比直接计算作答.
【详解】
依题意,三年级学生的总人数为,
从1500人中用分层随机抽样抽取容量为300的样本的抽样比为,
所以应抽取的三年级学生的人数为.
故选:C
3.C
【解析】
【分析】
根据分层抽样的性质、散点图的定义、频率分布直方图的特点依次判断命题即可.
【详解】
由分层抽样的性质可得,每个个体被被抽到的可能性与层数及分层无关,故命题①为假;
由散点图的定义可知,它是判断两个变量是否相关的一种重要方法和手段,故命题②为真;
在频率分布直方图中,每个小矩形的面积为该组的频率,又频率之和为1,所以各小长方形的面积之和为1,故命题③真.
故选:C
4.C
【解析】
【分析】
根据平均数、方差、中位数、极差的定义求解.
【详解】
解:对于选项A:因为,所以新数据的平均数为,故选项A正确,
对于选项B:因为,所以新数据的方差为,故选项B正确,
对于选项C:因为数据,,,的中位数为,所以新数据的中位数是,故选项C错误,
对于选项D:设数据,,,中最大,最小(其中,,,,则,所以新数据的极差是,故选项D正确,
故选:C.
5.C
【解析】
【分析】
根据简单随机抽样、分层抽样的适用条件进行分析判断.
【详解】
因为有关消费购买力的某项指标受家庭收入的影响,而社区家庭收入差距明显,所以①用分层抽样;
从10名体育特长生中抽取3人调查学习情况,个体之间差别不大,且总体和样本容量较小,所以②用简单随机抽样.
故选:C
6.B
【解析】
【分析】
根据直接求解.
【详解】
得
故选:B
7.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
8.B
【解析】
【分析】
利用总量乘以抽取比例即可得到样本容量;根据图表可知高中生近视率 从而估计抽取的高中生近视人数
【详解】
所有学生数为3000+4000+2000=9000,故样本容量为 9000×2%=180,
根据图甲以及抽取百分比可知,样本中高中生人数为2000×2%=40,
根据图乙可知,抽取的高中生近视人数为40×50%=20,
故选:B.
9.BD
【解析】
【分析】
根据众数、方差、平均数和极差的定义,算出对应数字特征即可判断答案.
【详解】
对A,设样本数据的众数为,则新样本数据的众数为,则A错误;
对B,样本数据的方差为,新样本数据的方差为,B正确;
对C,原数据的平均数,新数据的平均数,则C错误;
对D,不妨设样本数据中分别为最小值和最大值,极差为,则新样本数据中分别最小和最大,则极差,D正确.
故选:BD.
10.ABC
【解析】
【分析】
根据折线图上的数据可直接得到AB是正确的,10月1日至10月14日每日收益的中位数为故C也正确,10月8日和前一日比较收益增加最多,故D错误.
【详解】
由题中折线图可知,10月6日与10月9日的收益均为160元,故A正确;
由题中折线图可以看出,10月2日至10月5日的每日收益递增,故B正确;
10月1日至10月14日每日收益的中位数为(元),故C正确;
10月8日比前一日收益增加(元),
而10月5日比前一日收益增加(元),
10月8日和前一日比较收益增加177元,故D错误.
故选:ABC.
11.BD
【解析】
【分析】
A:根据图1中2021年1—2月的数据和5月到6月的利润率增速即可判断;
B:根据图1的2020年8月到2020年12月的每百元营业收入中的成本数据即可判断;
C:根据图2可以判断增速,但无法判断利润额的大小;
D:根据图2中营业收入增速数据即可判断.
【详解】
对于选项A,2021年1—2月的数据在一起,看不出是否增长,且从5月到6月增速相同,也没有递增,故选项A错误;
根据图1的信息即可判断B选项正确;
对于选项C,通过图2可知,国有控股企业的利润总额增速最大,利润总额是否最高不能确定,故选项C错误;
在图2中股份制企业的营业收入增速为27.0,确实是四类企业中最高值,故选项D正确.
故选:BD.
12.ABCD
【解析】
【分析】
根据收集数据的几种方法即可得出答案.
【详解】
收集数据主要有普查和抽样调查,
除此还有问卷调查﹑持续观察﹑做调查、查阅资料、做试验等;
接下来根据人数的多少以及调查的目的进行选择.
故选:ABCD
13.36
【解析】
【分析】
根据题意可得,解方程求出的值,再根据种型号的产品所占的比例,求出种型号的产品应抽取的数量.
【详解】
由题意,得,所以k=2,
所以C种型号的产品抽取的件数为12036.
故答案为:36.
14.
【解析】
【分析】
利用百分位数的计算方法即可求解.
【详解】
将以上数据从小到大排列为,,,,,,,;
%,则第25百分位数第项和第项的平均数,即为.
故答案为:.
15.##
【解析】
【分析】
根据平均数、方差公式计算可得;
【详解】
解:依题意全年级答对的有人,答错的有人,所以全年级的平均分为,所以方差为,则标准差为;
故答案为:
16.11
【解析】
【分析】
直接根据平均数的公式和中位数的定义计算得到答案.
【详解】
,解得.
数据从小到大排列得到:,中位数为.
故答案为:11.
17.(1)0.6
(2)3.7千米
【解析】
【分析】
(1)首先由频率分布直方图求出,求出后两组频率之和即得;
(2)设送餐距离较远的20%的外卖骑手对应的距离为,即距离不小于的频率为0.2,由最后一组的频率与后两组频率和可得,然后计算可得可得.
(1)
由,解得.
所以该平台该地区的外卖骑手的送餐距离小于3千米的频率为.
(2)
由频率分布直方图可得,最后1组的频率为0.1,
后2组的频率之和为.
设送餐距离较远的20%的外卖骑手对应的距离为千米,则.
所以,解得.
故该平台需要考虑的是送餐距离超过3.7千米的外卖骑手.
18.(1)该校高中生男生群体掌握冬奥会知识的平均水平高于女生
(2)
【解析】
【分析】
(1)先求出男生和女生的平均分、,比较两个数的大小即可;
(2)设男生中满分学生分别为,,,,女生满分学生分别为A,,利用列举法列出所有可能的结果和性别不同的结果,进而得出答案.
(1)
设男生和女生的平均得分分别为、,则
,
.
∵,∴该校高中生男生群体掌握冬奥会知识的平均水平高于女生.
(2)
由统计图可知,得分为100分的人数为6人,
设男生中满分学生分别为,,,,女生满分学生分别为A,,共6人,现从6人中随机抽取两人,共有如下15种可能:
,,,,,
,,,,
,,,
,,
,
其中性别不同的有如下8种可能:
,;,;,;,.
∴抽取的两名学生性别不同的概率为.
19.(1)证明见解析;
(2)证明见解析;
(3)证明见解析.
【解析】
【分析】
(1)利用平均数的定义及计算公式即证;
(2)利用平均数的含义及计算公式即证;
(3)利用平均数、方差的定义及计算公式即证;
(1)
根据平均数定义,,
故,
因此.
(2)
因为,,
所以.
因为,,
所以
.
(3)
方法一:由方差定义可得,由(2)可知,
所以
.
同理,于是
将代入化简得.
方法二:由题设,所以
.
同理,于是
将代入化简得.
20.(1)分;
(2)分布列见解析,期望为.
【解析】
【分析】
(1)根据题意,结合频率分布直方图的性质,求得,再利用平均数的计算公式,即可求解;
(2)根据题意得到6人中有人数学和物理两科都为“优秀”,得出的可能取值为,求得相应的概率,得出分布列,利用期望的公式,即可求解.
(1)
解:因为a,b,c成等差数列,且,所以,可得,
由频率分布直方图,可得,
所以,解得,所以,
所以估计甲班数学成绩的平均分为:
(分).
(2)
解:甲班中物理成绩为优秀的有5人,数学成绩为优秀的有人,
因为数学或物理成绩至少有一科为“优秀”的学生共有6人,
所以6人中有人数学和物理两科都为“优秀”,
从这6人中随机抽取3人,记表示抽到数学和入了两科成绩都是“优秀”的学生人数,则随机变量的可能取值为,
则,
,
所以的分布列为:
所以期望为.
21.(1)77;123
(2)74;138
【解析】
【分析】
(1)直接代公式求出平均数和方差;
(2)记这70名同学的平均成绩和方差分别为,,根据分层抽样中两组数据x,y的抽样比例求平均数和方差.
(1)
,
;
(2)
记这70名同学的平均成绩和方差分别为,,
分层抽样中两组数据x,y的抽样比例是,则总体均值为,
所以,,
总体方差,
.
22.(1);;;认可度等级为级的女性消费者人数为14;
(2)被选中的男性消费者人数为7,女性消费者人数为4.
【解析】
【分析】
(1)利用频率的概念及性质可求,,的值,进而可得女性消费者人数,再结合条件即得;
(2)由题可得认可度等级为级或级的男性消费者及女性消费者人数,再利用分层抽样的概念即求.
(1)
由表可知,,即.
由题可得男性消费者人数为,
所以,,
被调查者中,女性消费者人数为,
故认可度等级为级的女性消费者人数为.
所以,,,认可度等级为级的女性消费者人数为14;
(2)
由题可知认可度等级为级或级的男性消费者有人,认可度等级为级或级的女性消费者有人,
从中选取11人,则被选中的男性消费者人数为,女性消费者人数为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
