高中数学同步指导试卷苏教版(2019)必修第一册函数应用1 (word含解析)
文档属性
| 名称 | 高中数学同步指导试卷苏教版(2019)必修第一册函数应用1 (word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 804.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




文档简介
高中数学同步指导试卷苏教版(2019)必修第一册函数应用
一、单选题
1.已知函数在内有且仅有两个零点,则的取值范围是( )
A. B. C. D.
2.若关于x的方程有两个不相等的实根、,且满足,则实数t的取值范围是( )
A.(2,5) B.
C. D.
3.已知函数,,的零点分别为,,,则,,的大小关系是( ).
A. B.
C. D.
4.函数的大致图象是( )
A. B.
C. D.
5.已知,,函数的零点为c,则( )
A.c<a<b B.a<c<b C.b<a<c D.a<b<c
6.函数的零点所在的区间为( )
A. B. C. D.
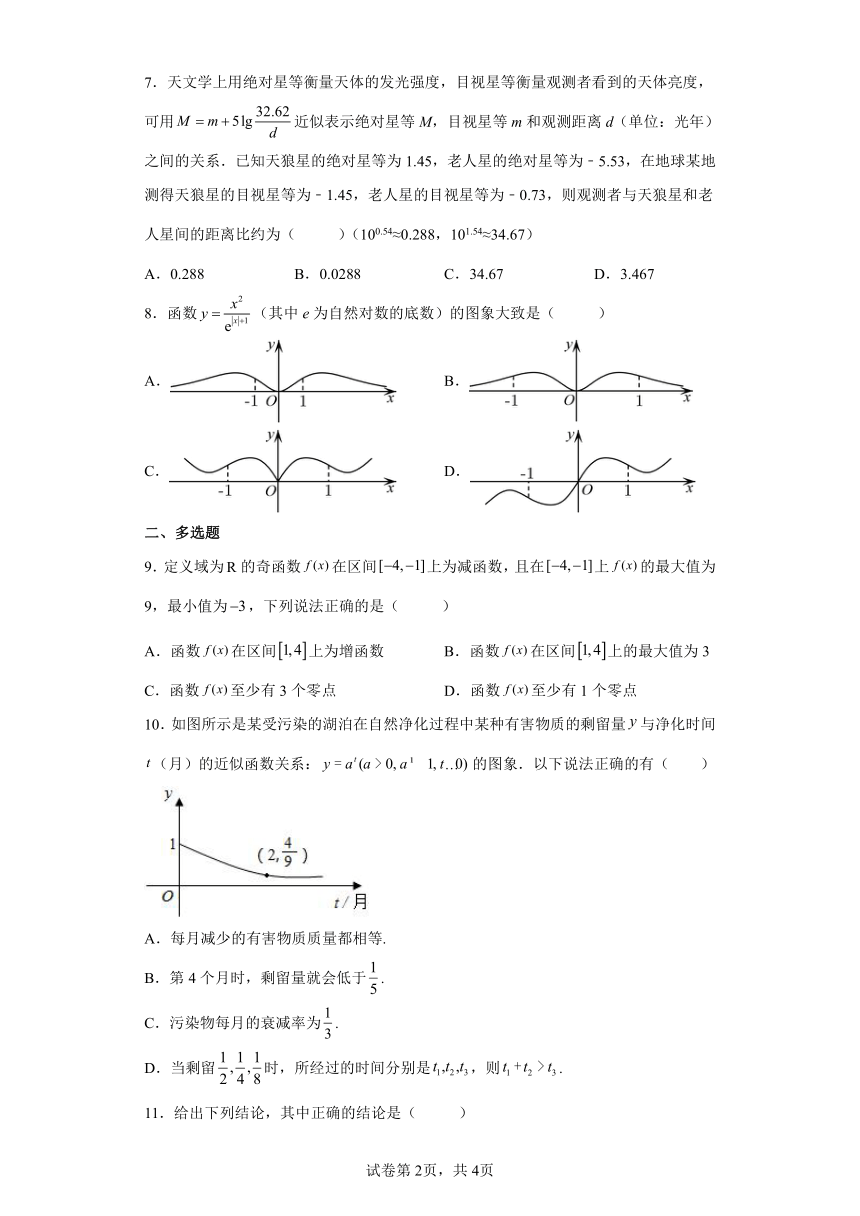
7.天文学上用绝对星等衡量天体的发光强度,目视星等衡量观测者看到的天体亮度,可用近似表示绝对星等M,目视星等m和观测距离d(单位:光年)之间的关系.已知天狼星的绝对星等为1.45,老人星的绝对星等为﹣5.53,在地球某地测得天狼星的目视星等为﹣1.45,老人星的目视星等为﹣0.73,则观测者与天狼星和老人星间的距离比约为( )(100.54≈0.288,101.54≈34.67)
A.0.288 B.0.0288 C.34.67 D.3.467
8.函数(其中e为自然对数的底数)的图象大致是( )
A. B.
C. D.
二、多选题
9.定义域为的奇函数在区间上为减函数,且在上的最大值为9,最小值为,下列说法正确的是( )
A.函数在区间上为增函数 B.函数在区间上的最大值为3
C.函数至少有3个零点 D.函数至少有1个零点
10.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量与净化时间(月)的近似函数关系:的图象.以下说法正确的有( )
A.每月减少的有害物质质量都相等.
B.第4个月时,剩留量就会低于.
C.污染物每月的衰减率为.
D.当剩留时,所经过的时间分别是,则.
11.给出下列结论,其中正确的结论是( )
A.函数的最大值为
B.已知函数(且)在上是减函数,则实数的取值范围是
C.函数满足,则
D.已知定义在上的奇函数在内有1010个零点,则函数的零点个数为2021
12.已知函数,则下列结论正确的有( )
A.若,则有2个零点 B.存在,使得有1个零点
C.存在,使得有3个零点 D.存在,使得有3个零点
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.函数的零点个数是________.
14.某地街道呈现东—西 南—北向的网格状,相邻街距都为1,两街道相交的点称为格点.若以互相垂直的两条街道为坐标轴建立平面直角坐标系,根据垃圾分类要求,下述格点为垃圾回收点:,,,,,.请确定一个格点(除回收点外)___________为垃圾集中回收站,使这6个回收点沿街道到回收站之间路程的和最短.
15.已知一等腰三角形的周长为12,则将该三角形的底边长y(单位:)表示为腰长x(单位:)的函数解析式为___________.(请注明函数的定义域)
16.函数的零点为______.
四、解答题
17.为进一步提倡“节能减排,绿色生态”,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺把二氧化碳转化为一种可利用的化工产品.已知该单位每月的二氧化碳处理量最少为300吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似地表示为,且每处理1吨二氧化碳得到可利用的化工产品价值为200元
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)设该单位月利润为G(元),请写出月利润G与月处理量的函数关系式,并求出最大利润.
18.若一元二次方程的一个根在区间内,另一个根在区间内,求实数的取值范围.
19.利用函数图象判断下列方程有没有实数根,有几个根.
(1);
(2);
(3).
20.已知函数,,g (x)与f (x)互为反函数.
(1)若函数在区间内有最小值,求实数m的取值范围;
(2)若函数y = h(g(x))在区间(1,2)内有唯一零点,求实数m的取值范围.
21.已知函数(且,)是偶函数.
(1)求k的值:
(2)若且,函数的图象与函数的图象都没有交点,求b的值;
(3)设函数,若函数与的图象有且只有一个公共点,求实数c的取值范围.
22.每年红嘴鸥都从西伯利亚飞越数千公里来到美丽的昆明过冬,科学家经过测量发现候鸟的飞行速度可以表示为函数,单位是,其中x表示候鸟每分钟耗氧量的单位数,常数x0表示测量过程中候鸟每分钟的耗氧偏差.(结果保留到整数位.参考数据:lg5≈0.70,31.4≈4.66)
(1)若x0=5,候鸟停下休息时,它每分钟的耗氧量为多少个单位.
(2)若雄鸟的飞行速度为1.3,雌鸟的飞行速度为0.8,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
根据给定条件确定的范围,求解不等式作答.
【详解】
由得,而当,时,,
又,函数在内有且仅有两个零点,
于是得,解得,
所以的取值范围是.
故选:D
2.B
【解析】
【分析】
令,由二次函数图象性质可知满足且计算即可得出结果.
【详解】
令,且,
所以只需满足且即可,
即且,解得,
故选:B.
3.A
【解析】
【分析】
将问题转化为,,与交点的横坐标大小的比较,通过数形结合的方式可确定大小关系.
【详解】
在同一坐标系中分别作出,,,的图象,如图所示.
由图可知,函数,,的零点分别为,,,
则,,,所以.
故选:A
4.D
【解析】
【分析】
根据奇偶性定义判断的对称性,并由及、增长速度关系,结合排除法确定函数图象.
【详解】
由且定义域为,故是偶函数,又,排除B、C;
当时,函数比增长得更快,排除A.
故选:D.
5.B
【解析】
【分析】
由函数零点存在定理可得,又,,从而即可得答案.
【详解】
解:因为在上单调递减,且,,
所以的零点所在区间为,即.又因为,,所以a<c<b.
故选:B.
6.C
【解析】
【分析】
分析函数的单调性,再利用零点存在性定理判断作答.
【详解】
函数的定义域为,且在上单调递增,
而,,
所以函数的零点所在的区间为.
故选:C
7.B
【解析】
【分析】
利用题中的数据,设出地球与天狼星的距离为d1,地球与老人星的距离为d2,即可解出.
【详解】
设地球与天狼星的距离为d1,地球与老人星的距离为d2,
由题意可得,
所以,
所以,
,
故选:B.
8.A
【解析】
【分析】
函数见式识图,该题型不是要求画函数图像,而是识别判断图像,因此只需要分辨即可.
【详解】
从表达式可以判断出,所以函数是偶函数,所以选项D不对;利用幂函数与指数函数的增长得快慢,即指数函数有爆炸函数之称,可以得到分母增长速度更快,所以当自变量趋于正无穷时,因变量趋于0,所以选项C不正确;对于选项AB在自变量1处的单调性不同,所以可以选择特值来判断,,所以B不对.
故选:A.
9.BD
【解析】
【分析】
根据奇函数的对称性判断AB,再由奇函数的性质及函数是否连续判断CD.
【详解】
因为奇函数的图象关于原点对称,所以函数在区间上为减函数,最大值为,故A错误,B正确;
由于无法确定函数是否连续,所以只能确定,函数至少有1个零点,故C错误,D正确.
故选:BD
10.BC
【解析】
【分析】
由于y=at(a>0且a≠1)(t≥0)的图象经过点(2,),所以=a2,从而可求得,然后根据解析式逐个分析判断即可
【详解】
解:∵y=at(a>0且a≠1)(t≥0)的图象经过点(2,),
∴=a2,∴a=,即.
故1月到2月,减少的有害物质质量为,2月到3月,减少的有害物质质量为, 故每月减少的有害物质质量都相等是错误的,即A错,
当t=4时,有害物质的剩留量,故B正确,
污染物每月的衰减率为,故C正确,
当剩留时,所经过的时间分别是t1,t2,t3,
则,,,
则,,,则t1+t2=t3,故D错,
故选:BC.
11.CD
【解析】
【分析】
利用指数函数的性质,结合函数的最值对A进行判断;利用对数函数的性质及复合函数的单调性对B进行判断;由得,,,对C进行判断;利用函数的零点与方程根的关系,结合奇函数的性质对D进行判断,从而得结论.
【详解】
对于A,因为,所以,因此有最小值,无最大值,所以A错误,
对于B,因为函数(且)在上是减函数,
所以,解得,实数的取值范围是,所以B错误,
对于C,由得,,,∴.所以C正确,
对于D,因为定义在上的奇函数在内有1010个零点,所以函数在内有1010个零点,而,因此函数的零点个数为,所以D正确,
故选:CD
12.ABD
【解析】
【分析】
画出函数图象,根据与的函数图象交点个数可判断.
【详解】
由题,的零点个数可转化为与的函数图象交点个数,
画出函数图象如下,
若,函数与在和各有一个交点,故有2个零点,故A正确;
当时,当,,
,,
故在上至少有一个零点,又,结合图象知,在上有两个零点,
即与有两个不同的交点,则当直线绕点顺时针旋转时,存在直线与的图象相切,即有1个零点,故B正确,
当时,与至多有两个交点,故C错误;
当时,如图,存在函数与的图象分别在和上分别有1个和2个交点,故存在 ,使得有3个零点,故D正确.
故选:ABD.
13.3
【解析】
【分析】
令f(x)=0求解即可.
【详解】
,方程有三个解,故f(x)有三个零点.
故答案为:3.
14.
【解析】
【分析】
根据题意,设满足题意得格点为,这6个回收点沿街道到回收站之间路程的和为,故,再分别求和的最小值时的即可得答案.
【详解】
解:设满足题意得格点为,这6个回收点沿街道到回收站之间路程的和为,
则,
令,由于其去掉绝对值为一次函数,故其最小值在区间端点值,
所以代入得,
所以当时,取得最小值,
同理,令,
代入得
所以当或时,取得最小值,
所以当,或时,这6个回收点沿街道到回收站之间路程的和最小,
由于是一个回收点,故舍去,
所以当,这6个回收点沿街道到回收站之间路程的和最小,
故格点为
故答案为:
15.
【解析】
【分析】
根据题意得,再结合两边之和大于第三边,底边长大于得,进而得答案.
【详解】
解:根据题意得,
由三角形两边之和大于第三边得,
所以,即,
又因为,解得
所以该三角形的底边长y(单位:)表示为腰长x(单位:)的函数解析式为
故答案为:
16.
【解析】
【分析】
先求出函数的定义域,通过解方程,再检验可得出答案.
【详解】
由定义域为
由,即,可得
解得或
又时,不满足方程
时满足条件.
故答案为:
17.(1)300吨;
(2);最大利润为35000元.
【解析】
【分析】
(1)每吨的平均处理成本为,因为,所以可根据基本不等式求最值,注意等于号取法;
(2)每月获利为,这是一个二次函数,利用对称轴与定义区间位置关系即可求出最大值.
(1)
由题意可知,二氧化碳每吨的平均处理成本为
当且仅当,即时等号成立,
故该单位月处理量为300吨时,才能使每吨的平均处理成本最低,最低成本为100元
(2)
由题意知,
,
函数在上单调递增,在上单调递减,
故当时,该单位每月获得最大利润为35000元.
18.
【解析】
【分析】
利用根的分布,列式求实数的取值范围.
【详解】
令,
则根据题意得,
∴.
故实数的取值范围.
19.(1)一元二次方程有两个不相等的实数根;
(2)一元二次方程有两个相等的实数根;
(3)一元二次方程没有实数根.
【解析】
【分析】
画出函数图象,根据函数图象与轴的交点即可判断.
(1)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有两个交点,
一元二次方程有两个不相等的实数根;
(2)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有一个交点,
一元二次方程有两个相等的实数根;
(3)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有没有交点,
一元二次方程没有实数根.
20.(1);
(2).
【解析】
【分析】
(1)根据二次函数的性质研究情况下的单调性和值域,根据对数复合函数的单调性及其开区间最值,列不等式求参数范围.
(2)将问题化为在内有唯一零点,利用二次函数的性质求参数范围即可.
(1)
由题设,,,
所以在定义域上递增,在上递减,在上递增,
又在内有最小值,
当,即时,在上递减,上递增,此时的值域为,则;
所以,可得;
当,即时,在上递减,上递增,此时是值域上的一个子区间,则;
所以开区间上不存在最值.
综上,.
(2)
由,则,要使在 (1,2)内有唯一零点,
所以在内有唯一零点,又开口向上且对称轴为,
所以,可得.
21.(1)
(2)0
(3)
【解析】
【分析】
(1)利用列方程,化简求得的值.
(2)由分离常数,结合对数函数的性质求得的值.
(3)由列方程,利用换元法,结合对分类讨论来求得的取值范围.
(1)
,即,
,
,
.
(2)
,即,
,
,
因为,
所以,,
,,
所以.
(3)
由题意得,有唯一解,
有唯一解.
令,,
有唯一解,
有唯一解.
设,
当时,,,,所以不符合题意;
当时,,,所以恰好一个大于的解:符合题意;
当时,,
解得或,
,符合题意;
,不符合题意,
综上,.
【点睛】
求解方程根、函数图象的交点、函数零点等问题,可考虑分离常数法来进行求解.如本题中第(2)问,与有个交点,转化为有个解,分离常数后,转化为与图象没有交点来进行求解.
22.(1)466个单位
(2)3倍
【解析】
【分析】
(1)将,代入函数解析式,求出的值即可答案;(2)设出雄鸟每分钟的耗氧量和雌鸟每分钟耗氧量,得到方程组,两式相减后得到,得到答案.
(1)
将,代入函数,得:,
因为,所以,所以,所以.
答:候鸟停下休息时,它每分钟的耗氧量约为466个单位.
(2)
设雄鸟每分钟的耗氧量为,雌鸟每分钟耗氧量为,由题意可得:
两式相减可得:,所以,即,
答:此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的3倍.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知函数在内有且仅有两个零点,则的取值范围是( )
A. B. C. D.
2.若关于x的方程有两个不相等的实根、,且满足,则实数t的取值范围是( )
A.(2,5) B.
C. D.
3.已知函数,,的零点分别为,,,则,,的大小关系是( ).
A. B.
C. D.
4.函数的大致图象是( )
A. B.
C. D.
5.已知,,函数的零点为c,则( )
A.c<a<b B.a<c<b C.b<a<c D.a<b<c
6.函数的零点所在的区间为( )
A. B. C. D.
7.天文学上用绝对星等衡量天体的发光强度,目视星等衡量观测者看到的天体亮度,可用近似表示绝对星等M,目视星等m和观测距离d(单位:光年)之间的关系.已知天狼星的绝对星等为1.45,老人星的绝对星等为﹣5.53,在地球某地测得天狼星的目视星等为﹣1.45,老人星的目视星等为﹣0.73,则观测者与天狼星和老人星间的距离比约为( )(100.54≈0.288,101.54≈34.67)
A.0.288 B.0.0288 C.34.67 D.3.467
8.函数(其中e为自然对数的底数)的图象大致是( )
A. B.
C. D.
二、多选题
9.定义域为的奇函数在区间上为减函数,且在上的最大值为9,最小值为,下列说法正确的是( )
A.函数在区间上为增函数 B.函数在区间上的最大值为3
C.函数至少有3个零点 D.函数至少有1个零点
10.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量与净化时间(月)的近似函数关系:的图象.以下说法正确的有( )
A.每月减少的有害物质质量都相等.
B.第4个月时,剩留量就会低于.
C.污染物每月的衰减率为.
D.当剩留时,所经过的时间分别是,则.
11.给出下列结论,其中正确的结论是( )
A.函数的最大值为
B.已知函数(且)在上是减函数,则实数的取值范围是
C.函数满足,则
D.已知定义在上的奇函数在内有1010个零点,则函数的零点个数为2021
12.已知函数,则下列结论正确的有( )
A.若,则有2个零点 B.存在,使得有1个零点
C.存在,使得有3个零点 D.存在,使得有3个零点
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.函数的零点个数是________.
14.某地街道呈现东—西 南—北向的网格状,相邻街距都为1,两街道相交的点称为格点.若以互相垂直的两条街道为坐标轴建立平面直角坐标系,根据垃圾分类要求,下述格点为垃圾回收点:,,,,,.请确定一个格点(除回收点外)___________为垃圾集中回收站,使这6个回收点沿街道到回收站之间路程的和最短.
15.已知一等腰三角形的周长为12,则将该三角形的底边长y(单位:)表示为腰长x(单位:)的函数解析式为___________.(请注明函数的定义域)
16.函数的零点为______.
四、解答题
17.为进一步提倡“节能减排,绿色生态”,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺把二氧化碳转化为一种可利用的化工产品.已知该单位每月的二氧化碳处理量最少为300吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似地表示为,且每处理1吨二氧化碳得到可利用的化工产品价值为200元
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)设该单位月利润为G(元),请写出月利润G与月处理量的函数关系式,并求出最大利润.
18.若一元二次方程的一个根在区间内,另一个根在区间内,求实数的取值范围.
19.利用函数图象判断下列方程有没有实数根,有几个根.
(1);
(2);
(3).
20.已知函数,,g (x)与f (x)互为反函数.
(1)若函数在区间内有最小值,求实数m的取值范围;
(2)若函数y = h(g(x))在区间(1,2)内有唯一零点,求实数m的取值范围.
21.已知函数(且,)是偶函数.
(1)求k的值:
(2)若且,函数的图象与函数的图象都没有交点,求b的值;
(3)设函数,若函数与的图象有且只有一个公共点,求实数c的取值范围.
22.每年红嘴鸥都从西伯利亚飞越数千公里来到美丽的昆明过冬,科学家经过测量发现候鸟的飞行速度可以表示为函数,单位是,其中x表示候鸟每分钟耗氧量的单位数,常数x0表示测量过程中候鸟每分钟的耗氧偏差.(结果保留到整数位.参考数据:lg5≈0.70,31.4≈4.66)
(1)若x0=5,候鸟停下休息时,它每分钟的耗氧量为多少个单位.
(2)若雄鸟的飞行速度为1.3,雌鸟的飞行速度为0.8,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
根据给定条件确定的范围,求解不等式作答.
【详解】
由得,而当,时,,
又,函数在内有且仅有两个零点,
于是得,解得,
所以的取值范围是.
故选:D
2.B
【解析】
【分析】
令,由二次函数图象性质可知满足且计算即可得出结果.
【详解】
令,且,
所以只需满足且即可,
即且,解得,
故选:B.
3.A
【解析】
【分析】
将问题转化为,,与交点的横坐标大小的比较,通过数形结合的方式可确定大小关系.
【详解】
在同一坐标系中分别作出,,,的图象,如图所示.
由图可知,函数,,的零点分别为,,,
则,,,所以.
故选:A
4.D
【解析】
【分析】
根据奇偶性定义判断的对称性,并由及、增长速度关系,结合排除法确定函数图象.
【详解】
由且定义域为,故是偶函数,又,排除B、C;
当时,函数比增长得更快,排除A.
故选:D.
5.B
【解析】
【分析】
由函数零点存在定理可得,又,,从而即可得答案.
【详解】
解:因为在上单调递减,且,,
所以的零点所在区间为,即.又因为,,所以a<c<b.
故选:B.
6.C
【解析】
【分析】
分析函数的单调性,再利用零点存在性定理判断作答.
【详解】
函数的定义域为,且在上单调递增,
而,,
所以函数的零点所在的区间为.
故选:C
7.B
【解析】
【分析】
利用题中的数据,设出地球与天狼星的距离为d1,地球与老人星的距离为d2,即可解出.
【详解】
设地球与天狼星的距离为d1,地球与老人星的距离为d2,
由题意可得,
所以,
所以,
,
故选:B.
8.A
【解析】
【分析】
函数见式识图,该题型不是要求画函数图像,而是识别判断图像,因此只需要分辨即可.
【详解】
从表达式可以判断出,所以函数是偶函数,所以选项D不对;利用幂函数与指数函数的增长得快慢,即指数函数有爆炸函数之称,可以得到分母增长速度更快,所以当自变量趋于正无穷时,因变量趋于0,所以选项C不正确;对于选项AB在自变量1处的单调性不同,所以可以选择特值来判断,,所以B不对.
故选:A.
9.BD
【解析】
【分析】
根据奇函数的对称性判断AB,再由奇函数的性质及函数是否连续判断CD.
【详解】
因为奇函数的图象关于原点对称,所以函数在区间上为减函数,最大值为,故A错误,B正确;
由于无法确定函数是否连续,所以只能确定,函数至少有1个零点,故C错误,D正确.
故选:BD
10.BC
【解析】
【分析】
由于y=at(a>0且a≠1)(t≥0)的图象经过点(2,),所以=a2,从而可求得,然后根据解析式逐个分析判断即可
【详解】
解:∵y=at(a>0且a≠1)(t≥0)的图象经过点(2,),
∴=a2,∴a=,即.
故1月到2月,减少的有害物质质量为,2月到3月,减少的有害物质质量为, 故每月减少的有害物质质量都相等是错误的,即A错,
当t=4时,有害物质的剩留量,故B正确,
污染物每月的衰减率为,故C正确,
当剩留时,所经过的时间分别是t1,t2,t3,
则,,,
则,,,则t1+t2=t3,故D错,
故选:BC.
11.CD
【解析】
【分析】
利用指数函数的性质,结合函数的最值对A进行判断;利用对数函数的性质及复合函数的单调性对B进行判断;由得,,,对C进行判断;利用函数的零点与方程根的关系,结合奇函数的性质对D进行判断,从而得结论.
【详解】
对于A,因为,所以,因此有最小值,无最大值,所以A错误,
对于B,因为函数(且)在上是减函数,
所以,解得,实数的取值范围是,所以B错误,
对于C,由得,,,∴.所以C正确,
对于D,因为定义在上的奇函数在内有1010个零点,所以函数在内有1010个零点,而,因此函数的零点个数为,所以D正确,
故选:CD
12.ABD
【解析】
【分析】
画出函数图象,根据与的函数图象交点个数可判断.
【详解】
由题,的零点个数可转化为与的函数图象交点个数,
画出函数图象如下,
若,函数与在和各有一个交点,故有2个零点,故A正确;
当时,当,,
,,
故在上至少有一个零点,又,结合图象知,在上有两个零点,
即与有两个不同的交点,则当直线绕点顺时针旋转时,存在直线与的图象相切,即有1个零点,故B正确,
当时,与至多有两个交点,故C错误;
当时,如图,存在函数与的图象分别在和上分别有1个和2个交点,故存在 ,使得有3个零点,故D正确.
故选:ABD.
13.3
【解析】
【分析】
令f(x)=0求解即可.
【详解】
,方程有三个解,故f(x)有三个零点.
故答案为:3.
14.
【解析】
【分析】
根据题意,设满足题意得格点为,这6个回收点沿街道到回收站之间路程的和为,故,再分别求和的最小值时的即可得答案.
【详解】
解:设满足题意得格点为,这6个回收点沿街道到回收站之间路程的和为,
则,
令,由于其去掉绝对值为一次函数,故其最小值在区间端点值,
所以代入得,
所以当时,取得最小值,
同理,令,
代入得
所以当或时,取得最小值,
所以当,或时,这6个回收点沿街道到回收站之间路程的和最小,
由于是一个回收点,故舍去,
所以当,这6个回收点沿街道到回收站之间路程的和最小,
故格点为
故答案为:
15.
【解析】
【分析】
根据题意得,再结合两边之和大于第三边,底边长大于得,进而得答案.
【详解】
解:根据题意得,
由三角形两边之和大于第三边得,
所以,即,
又因为,解得
所以该三角形的底边长y(单位:)表示为腰长x(单位:)的函数解析式为
故答案为:
16.
【解析】
【分析】
先求出函数的定义域,通过解方程,再检验可得出答案.
【详解】
由定义域为
由,即,可得
解得或
又时,不满足方程
时满足条件.
故答案为:
17.(1)300吨;
(2);最大利润为35000元.
【解析】
【分析】
(1)每吨的平均处理成本为,因为,所以可根据基本不等式求最值,注意等于号取法;
(2)每月获利为,这是一个二次函数,利用对称轴与定义区间位置关系即可求出最大值.
(1)
由题意可知,二氧化碳每吨的平均处理成本为
当且仅当,即时等号成立,
故该单位月处理量为300吨时,才能使每吨的平均处理成本最低,最低成本为100元
(2)
由题意知,
,
函数在上单调递增,在上单调递减,
故当时,该单位每月获得最大利润为35000元.
18.
【解析】
【分析】
利用根的分布,列式求实数的取值范围.
【详解】
令,
则根据题意得,
∴.
故实数的取值范围.
19.(1)一元二次方程有两个不相等的实数根;
(2)一元二次方程有两个相等的实数根;
(3)一元二次方程没有实数根.
【解析】
【分析】
画出函数图象,根据函数图象与轴的交点即可判断.
(1)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有两个交点,
一元二次方程有两个不相等的实数根;
(2)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有一个交点,
一元二次方程有两个相等的实数根;
(3)
解:画出函数的图象如图:
由图象可知,函数的图象与轴有没有交点,
一元二次方程没有实数根.
20.(1);
(2).
【解析】
【分析】
(1)根据二次函数的性质研究情况下的单调性和值域,根据对数复合函数的单调性及其开区间最值,列不等式求参数范围.
(2)将问题化为在内有唯一零点,利用二次函数的性质求参数范围即可.
(1)
由题设,,,
所以在定义域上递增,在上递减,在上递增,
又在内有最小值,
当,即时,在上递减,上递增,此时的值域为,则;
所以,可得;
当,即时,在上递减,上递增,此时是值域上的一个子区间,则;
所以开区间上不存在最值.
综上,.
(2)
由,则,要使在 (1,2)内有唯一零点,
所以在内有唯一零点,又开口向上且对称轴为,
所以,可得.
21.(1)
(2)0
(3)
【解析】
【分析】
(1)利用列方程,化简求得的值.
(2)由分离常数,结合对数函数的性质求得的值.
(3)由列方程,利用换元法,结合对分类讨论来求得的取值范围.
(1)
,即,
,
,
.
(2)
,即,
,
,
因为,
所以,,
,,
所以.
(3)
由题意得,有唯一解,
有唯一解.
令,,
有唯一解,
有唯一解.
设,
当时,,,,所以不符合题意;
当时,,,所以恰好一个大于的解:符合题意;
当时,,
解得或,
,符合题意;
,不符合题意,
综上,.
【点睛】
求解方程根、函数图象的交点、函数零点等问题,可考虑分离常数法来进行求解.如本题中第(2)问,与有个交点,转化为有个解,分离常数后,转化为与图象没有交点来进行求解.
22.(1)466个单位
(2)3倍
【解析】
【分析】
(1)将,代入函数解析式,求出的值即可答案;(2)设出雄鸟每分钟的耗氧量和雌鸟每分钟耗氧量,得到方程组,两式相减后得到,得到答案.
(1)
将,代入函数,得:,
因为,所以,所以,所以.
答:候鸟停下休息时,它每分钟的耗氧量约为466个单位.
(2)
设雄鸟每分钟的耗氧量为,雌鸟每分钟耗氧量为,由题意可得:
两式相减可得:,所以,即,
答:此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的3倍.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
