高中数学同步指导试卷苏教版(2019)必修第一册函数应用2 (word含解析)
文档属性
| 名称 | 高中数学同步指导试卷苏教版(2019)必修第一册函数应用2 (word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 883.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 08:31:52 | ||
图片预览




文档简介
高中数学同步指导试卷苏教版(2019)必修第一册函数应用
一、单选题
1.若关于的方程的实数解为,则所在区间可以是( )
A. B. C. D.
2.函数的零点所在的区间为( )
A. B.
C. D.
3.某商场若将进货单价为8元的商品按每件10元出售,则每天可销售100件.现准备采用提高售价的方法来增加利润,已知这种商品每件的售价每提高1元,每天的销量就要减少10件.要使该商场每天销售该商品所得的利润最大,则该商品每件的售价为( )
A.12元 B.14元 C.15元 D.16元
4.某种放射性物质不断变化为其他物质,每经过一年剩留的该种放射性物质的质量约是原来的,估计经过多少年,该物质剩留的是原来的?( )
(参考数据:)
A.16 B.17 C.18 D.19
5.已知函数,,的零点分别为,,,则,,的大小关系是( ).
A. B.
C. D.
6.函数的零点所在区间为:( )
A. B.
C. D.
7.已知函数,若方程恰好有四个实根,则实数k的取值范围是( )
A. B.
C. D.
8.某种水果的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(…为自然对数的底数,k,b为常数).若该水果在0℃的保鲜时间是192小时,在14℃的保鲜时间是48小时,则该水果在21℃的保鲜时间是( )
A.16小时 B.20小时 C.24小时 D.28小时
二、多选题
9.若函数在区间上的图像为一条不间断的曲线,则下列说法中正确的是( )
A.若,则存在实数,使得
B.若,则不存在实数,使得
C.若对任意的实数,则
D.若存在实数,则
10.已知是定义在R上的偶函数,且在上单调递增,则下列结论正确的是( )
A.在上单调递减 B.最多有两个零点
C. D.若实数a满足,则
11.已知函数,则( )
A.
B.
C.若函数恰有个零点,则
D.当时,
12.高斯是世界最具盛名的数学家之一,一生成就极为丰硕,以他们名字“高斯”命名的成果有110个之多,属数学家之最,其中有“高斯函数”的定义为:设,用表示不超过x的最大整数,则称为高斯函数,例如,.已知函数,函数,则( )
A.函数的值域是{0,1,2} B.函数是周期函数
C.函数的图象关于y轴对称 D.函数只有一个零点
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.若函数的两个零点是2和3,则不等式 的解集为________ .
14.某地为践行“绿水青山就是金山银山”的环保理念,大力展开植树造林.假设一片森林原来的面积为亩,计划每年种植一些树苗,且森林面积的年增长率相同,当面积是原来的2倍时,所用时间是10年.为使森林面积至少达到亩,至少需要植树造林______年(精确到整数).(参考数据:,)
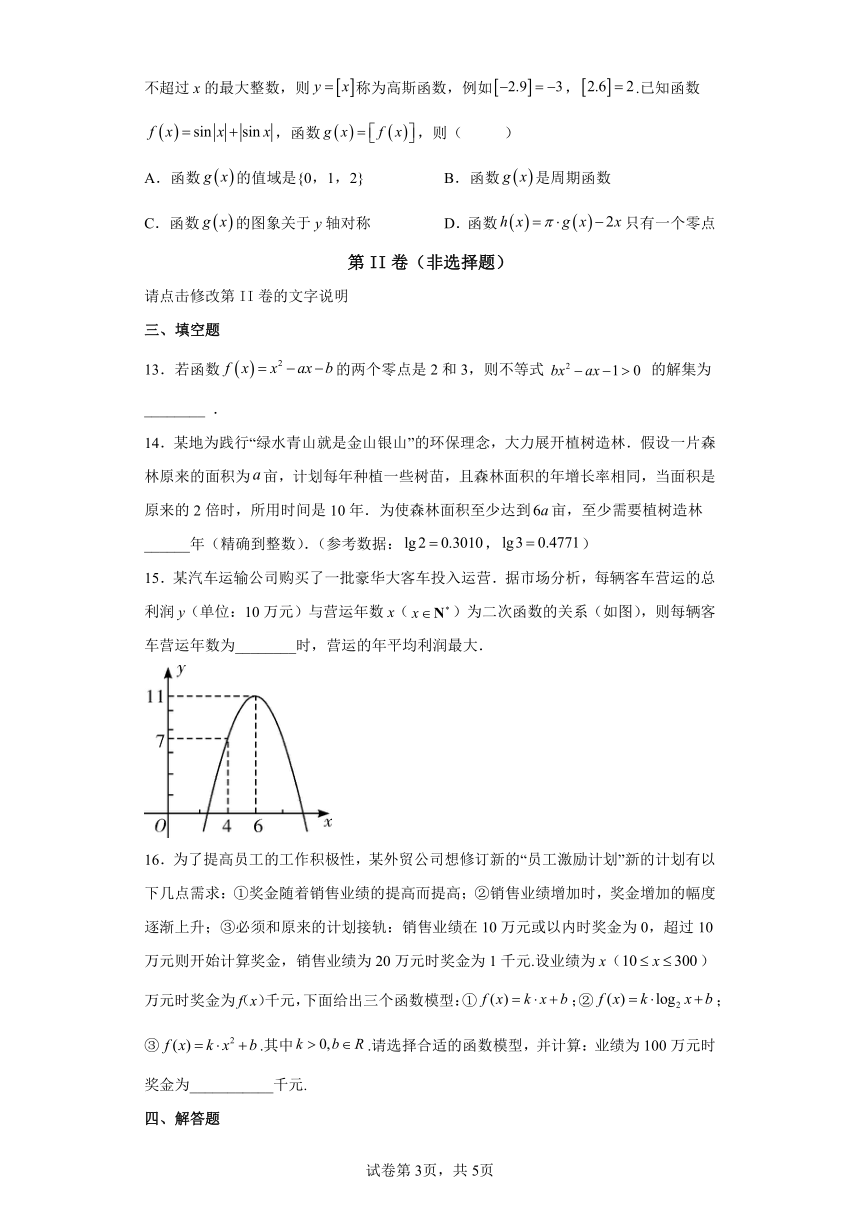
15.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x()为二次函数的关系(如图),则每辆客车营运年数为________时,营运的年平均利润最大.
16.为了提高员工的工作积极性,某外贸公司想修订新的“员工激励计划”新的计划有以下几点需求:①奖金随着销售业绩的提高而提高;②销售业绩增加时,奖金增加的幅度逐渐上升;③必须和原来的计划接轨:销售业绩在10万元或以内时奖金为0,超过10万元则开始计算奖金,销售业绩为20万元时奖金为1千元.设业绩为x()万元时奖金为f(x)千元,下面给出三个函数模型:①;②;③.其中.请选择合适的函数模型,并计算:业绩为100万元时奖金为___________千元.
四、解答题
17.2021年12月9日15时40分,神舟十三号“天宫课堂”第一课开讲!受“天宫课堂”的激励与鼓舞,某同学对航天知识产生了浓厚的兴趣.通过查阅资料,他发现在不考虑气动阻力和地球引力等造成的影响时,火箭是目前唯一能使物体达到宇宙速度,克服或摆脱地 球引力,进人宇宙空间的运载工具.早在1903年齐奥尔科夫斯基就推导出单级火箭的最大理想速度公式: ,被称为齐奥尔科夫斯基公式,其中为发动机的喷射速度,和分别是火箭的初始质量和发动机熄火(推进剂用完 )时的质量.被称为火箭的质量比.
(1)某单级火箭的初始质量为160吨,发动机的喷射速度为2千米/秒,发动机熄火时的 质量为40吨,求该单级火箭的最大理想速度(保留2位有效数字);
(2)根据现在的科学水平,通常单级火箭的质量比不超过10.如果某单级火箭的发动机的喷射速度为2千米/秒,请判断该单级火箭的最大理想速度能否超过第一宇宙速度千米/秒,并说明理由.(参考数据:,无理数)
18.设,,若函数恰好有三个不同的零点,分别为 .
(1)求的取值范围;
(2)求的值.
19.对于函数,若在其定义域内存在实数,,使得成立,则称是“跃点”函数,并称是函数的1个“跃点”.
(1)求证:函数在上是“1跃点”函数;
(2)若函数在上存在2个“1跃点”,求实数的取值范围;
(3)是否同时存在实数和正整数使得函数在上有2022个“跃点”?若存在,请求出和满足的条件;若不存在,请说明理由.
20.某校数学兴趣小组,在过去一年一直在研究学校附近池塘里某种水生植物的面积变化情况,自2021年元旦开始测量该水生植物的面积,此后每隔一个月(每月月底)测量一次,通过一年的观察发现,自2021年元旦起,该水生植物在池塘里面积增加的速度是越来越快的.最初测得该水生植物面积为,二月底测得该水生植物的面积为,三月底测得该水生植物的面积为,该水生植物的面积y(单位:)与时间x(单位:月)的关系有两个函数模型可供选择,一个是同学甲提出的;另一个是同学乙提出的,记2021年元旦最初测量时间x的值为0.
(1)根据本学期所学,请你判断哪个同学提出的函数模型更适合?并求出该函数模型的解析式;
(2)池塘中该水生植物面积应该在几月份起是元旦开始研究时该水生植物面积的10倍以上?(参考数据:,)
21.我市某运输公司为积极响应国家节能减排的号召,年初以每台12800元的价格购入一批风能发电机.经测算,每台发电机每年的发电收益约7200元,已知每台发电机使用年后的累计维修保养费用为元,且满足关系式(,为常数).已知该批发电机第1年每台的维修保养费用为1000元,前2年每台的累计维修保养费用为2400元.设每台发电机使用年后的总利润为元.
(1)求关于的函数关系式;
(2)问每台发电机在第几年的年平均利润最大?(注:年平均利润总利润年数)
22.国际上常用恩格尔系数r来衡量一个国家或地区的人民生活水平.根据恩格尔系数的大小,可将各个国家或地区的生活水平依次划分为:贫困,温饱,小康,富裕,最富裕等五个级别,其划分标准如下表:
级别 贫困 温饱 小康 富裕 最富裕
标准 r>60% 50%<r≤60% 40%<r=50% 30%<r≤40% r≤30%
某地区每年底计算一次恩格尔系数,已知该地区2000年底的恩格尔系数为60%.统计资料表明:该地区食物支出金额年平均增长4%,总支出金额年平均增长.根据上述材料,回答以下问题.
(1)该地区在2010年底是否已经达到小康水平,说明理由;
(2)最快到哪一年底,该地区达到富裕水平?
参考数据:,,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
构造函数,分析函数在上的单调性,结合零点存在定理可得出结论.
【详解】
由可得,设,
因为函数、在上均为增函数,故函数在上也为增函数,
因为,,故.
故选:C.
2.C
【解析】
【分析】
结合函数的单调性,利用零点存在定理可判断出函数的零点所在的区间.
【详解】
∵函数,
∴函数在上单调递增,
又,,,
故函数的零点所在区间为.
故选:C.
3.B
【解析】
【分析】
设该商品每件的售价为x元,根据给定条件列出关于x的函数关系,借助函数最值求解作答.
【详解】
设该商品每件的售价为x元,则每件商品售出所获利润为元,销售量为件,
商场每天销售该商品所得的利润,
当时,(元),
所以该商品每件的售价为14元.
故选:B
4.A
【解析】
【分析】
根据题意列出剩留量和年份的关系式,结合对数的运算,即可求解.
【详解】
设该种放射性物质初始质量为,经过年,剩留量变为,
则可建立模型为,
即,
所以大约经过16年,该物质剩留的是原来的.
故选:A.
5.A
【解析】
【分析】
将问题转化为,,与交点的横坐标大小的比较,通过数形结合的方式可确定大小关系.
【详解】
在同一坐标系中分别作出,,,的图象,如图所示.
由图可知,函数,,的零点分别为,,,
则,,,所以.
故选:A
6.C
【解析】
【分析】
利用函数的单调性及零点存在定理即得.
【详解】
因为,
所以函数单调递减,
,
∴函数的零点所在区间为.
故选:C.
7.D
【解析】
【分析】
画出的图象,根据与的图象有个交点来求得的取值范围.
【详解】
当时,,的图象向右平移2个单位,
再把纵坐标变为原来的2倍,得到的图象,也即在区间上的图象.
以此类推,则在区间上的图象如图所示.
记,若方程恰好有四个实根,
则函数与 的图象有且只有四个公共点,
由图得,点,,,,则,,,,则,所以与的图象有且只有四个公共点时.
故选:D
8.C
【解析】
【分析】
利用条件得到,,从而求出x=21的函数值.
【详解】
函数中,当时,当时,
所以,则,所以当时,.
故选:C
9.AC
【解析】
【分析】
由零点存在性定理判断A选项,BD选项可以举出反例,C选项,得到在上的图象与轴没有交点,进而作出判断.
【详解】
由零点存在性定理可知:A正确;
如图1,满足,且存在实数,使得,故B错误;
因为对任意的实数,故在上的图象与轴没有交点,故在上的图象在x轴上方或在x轴下方,故,C正确;
如图1,存在实数,而,故D错误.
故选:AC
10.ACD
【解析】
【分析】
A.由偶函数在对称区间上的单调性判断;B.举例判断;C.由偶函数得到 ,再利用单调性判断;D. 由偶函数得到 ,再利用单调性求解判断;
【详解】
因为是定义在R上的偶函数,且在上单调递增,
所以在上单调递减,故A正确;
如,令,得或或,函数有三个零点,故B错误;
,因为,所以,故C正确;
若实数a满足,即,则,解得,故D正确;
故选:ACD
11.BCD
【解析】
【分析】
直接计算、的值,可判断A选项;利用函数在上的单调性可判断B选项;数形结合求出的取值范围,可判断C选项;求出不等式在时的解,数形结合可判断D选项的正误.
【详解】
对于A选项,,,故,A错;
对于B选项,当时,,此时函数单调递增,
当时,,此时函数单调递减,
因为,,,
且,,
,
因为,所以,,
即,所以,,
且,,,
所以,,
即,B对;
对于C选项,作出函数与的图象如下图所示:
由图可知,当时,直线与函数的图象至多有两个交点,不合乎题意,
当时,直线与函数的图象有无数个交点,不合乎题意,
由题意可知,直线与函数的图象有个交点,
则,解得,C对;
对于D选项,当时,由可得,解得,
当时,,结合图象可知当时,,D对.
故选:BCD.
12.ACD
【解析】
【分析】
先研究函数的奇偶性,作出函数的图象,作出函数的图象判断选项A、B、C的正确性,再分类讨论判断方程的根的个数得解.
【详解】
首先分析函数性质,为偶函数,故只需考虑x轴非负半轴图象;
时,,
所以图象如下:
因为,
所以也是偶函数,C正确;
从而只需考虑在x轴非负半轴图象;观察到在x轴非负半轴上的图象以为单位反复出现,故只需考虑 在上的图象;
决定取值的分界点是取整数的位置:
由,
,
,
得:,值域为,A正确;
作图象:
由图可知,图象在原点处的形状与左右两侧都不同,不是周期函数;故B错误;
,作直线,
观察图象得知,该直线所过定点,
恰好不在图象上,两条曲线只交于原点,故D正确.
故选:ACD.
13.
【解析】
【分析】
先根据根与系数的关系求出a,b,进而解出不等式即可.
【详解】
根据题意,,则不等式可化为.
故答案为:.
14.26.
【解析】
【分析】
先由已知求增长率,再求达到所需年数.
【详解】
设年增长率为,所求年数为,
根据已知:,解得,
又,所以,
至少需要植树造林26年.
故答案为:26.
15.5
【解析】
【分析】
首先根据题意得到二次函数的解析式为,再利用基本不等式求解的最大值即可.
【详解】
根据题意得到:抛物线的顶点为,过点,开口向下,
设二次函数的解析式为,
所以,解得,即,
则营运的年平均利润,
当且仅当,即时取等号.
故答案为:5.
16.
【解析】
【分析】
根据“销售业绩增加时,奖金增加的幅度逐渐上升”可知,给出的模型中只有满足,“必须和原来的计划接轨”表明,当时,,再结合“销售业绩为20万元时奖金为1千元”可知,当时,,然后解出方程即可
【详解】
根据题意,当时,给出三个函数模型均满足“奖金随着销售业绩的提高而提高”,而只有模型“”满足“销售业绩增加时,奖金增加的幅度逐渐上升”,故模型选择:
根据题意,则有:
解得:
则模型为:
当时,
故答案为:
17.(1)千米/秒;
(2)该单级火箭最大理想速度不可以超过第一宇宙速度千米/秒,理由见解析.
【解析】
【分析】
(1)由题可知,,,代入即求;
(2)利用条件可求,即得.
(1)
,,,
该单级火箭的最大理想速度为千米/秒.
(2)
,,
,
,
,
.
该单级火箭最大理想速度不可以超过第一宇宙速度千米/秒.
18.(1);
(2)。
【解析】
【分析】
(1)由函数与方程的关系转化为两个函数的交点问题,利用数形结合即得;
(2)根据三角函数的对称性,求出函数的对称轴,结合图象进行求解即可.
(1)
由得,
若函数恰好有三个不同的零点,等价于函数与的图象有三个交点,作出函数的图象如图,
由题知,则,
即的取值范围为.
(2)
由,得对称轴,
,由,解得,
当时,对称轴,时,对称轴,
由图象可知,点、关于直线对称,则,
点、关于直线对称,则,
因此,.
19.(1)证明见详解
(2)
(3)存在,或或
【解析】
【分析】
(1)将要证明问题转化为方程在上有解,构造函数转化为函数零点问题,结合零点存在性定理可证;
(2)原问题等价于方程在由两个根,然后构造二次函数,转化为零点分布问题可解;
(3)将问题转化为方程在上有2022个实数根,再转化为两个函数交点个数问题,然后可解.
(1)
因为
整理得,令,
因为,所以在区间有零点,即存在,使得,即存在,使得,
所以,函数在上是“1跃点”函数
(2)
函数在上存在2个“1跃点”方程在上有两个实数根,
即在上有两个实数根,
令,则
解得或,
所以的取值范围是
(3)
由,得,
即
因为函数在上有2022个“跃点”,所以方程在上有2022个解,即函数与的图象有2022个交点.
所以或或
即或或
20.(1)甲同学提出的函数模型满足要求,
(2)池塘中该水生植物面积应该在6月起是去年元旦开始研究时该水生植物面积的10倍以上
【解析】
【分析】
(1)根据水生植物面积的增长变化结合函数的增长变化快慢选择即可;
(2)根据题意建立不等式,利用取对数的方法求解即可.
(1)
因为两个函数模型,在上都是增函数.
随着x的增大,的函数值增加的越来越快,而的函数值增加的越来越慢.
因为在池塘里该水生植物蔓延的速度是越来越快,即随着时间增加,该水生植物的面积增加的越来越快,
所以,甲同学提出的函数模型满足要求.
由题意知,解得,,
所以,
(2)
一月底水深植物面积为
由,解得
又
故.
所以,池塘中该水生植物面积应该在6月起是去年元旦开始研究时该水生植物面积的10倍以上.
21.(1),
(2)第8年的年平均利润最大.
【解析】
【分析】
(1)首先根据题意得到,解方程组得到,再根据题意即可得到函数的解析式.
(2)利用基本不等式求解即可.
(1)
由题知:,解得,
所以.
,.
(2)
设平均利润,所以,
所以.
当且仅当,即时取等号.
所以每台发电机在第8年的年平均利润最大.
22.(1)已经达到,理由见解析
(2)2022年
【解析】
【分析】
(1)根据该地区食物支出金额年平均增长4%,总支出金额年平均增长的比例列式求解,判断十年后是否达到即可.
(2)假设经过n年,该地区达到富裕水平,列式,利用指对数互化解不等式即可.
(1)
该地区2000年底的恩格尔系数为%,
则2010年底的思格尔系数为
因为
所以1,
则
所以.
所以该地区在2010年底已经达到小康水平.
(2)
从2000年底算起,设经过n年,该地区达到富裕水平
则,
故,即.
化为.
因为,则In,所以.
因为
.
所以.
所以,最快到2022年底,该地区达到富裕水平.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若关于的方程的实数解为,则所在区间可以是( )
A. B. C. D.
2.函数的零点所在的区间为( )
A. B.
C. D.
3.某商场若将进货单价为8元的商品按每件10元出售,则每天可销售100件.现准备采用提高售价的方法来增加利润,已知这种商品每件的售价每提高1元,每天的销量就要减少10件.要使该商场每天销售该商品所得的利润最大,则该商品每件的售价为( )
A.12元 B.14元 C.15元 D.16元
4.某种放射性物质不断变化为其他物质,每经过一年剩留的该种放射性物质的质量约是原来的,估计经过多少年,该物质剩留的是原来的?( )
(参考数据:)
A.16 B.17 C.18 D.19
5.已知函数,,的零点分别为,,,则,,的大小关系是( ).
A. B.
C. D.
6.函数的零点所在区间为:( )
A. B.
C. D.
7.已知函数,若方程恰好有四个实根,则实数k的取值范围是( )
A. B.
C. D.
8.某种水果的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(…为自然对数的底数,k,b为常数).若该水果在0℃的保鲜时间是192小时,在14℃的保鲜时间是48小时,则该水果在21℃的保鲜时间是( )
A.16小时 B.20小时 C.24小时 D.28小时
二、多选题
9.若函数在区间上的图像为一条不间断的曲线,则下列说法中正确的是( )
A.若,则存在实数,使得
B.若,则不存在实数,使得
C.若对任意的实数,则
D.若存在实数,则
10.已知是定义在R上的偶函数,且在上单调递增,则下列结论正确的是( )
A.在上单调递减 B.最多有两个零点
C. D.若实数a满足,则
11.已知函数,则( )
A.
B.
C.若函数恰有个零点,则
D.当时,
12.高斯是世界最具盛名的数学家之一,一生成就极为丰硕,以他们名字“高斯”命名的成果有110个之多,属数学家之最,其中有“高斯函数”的定义为:设,用表示不超过x的最大整数,则称为高斯函数,例如,.已知函数,函数,则( )
A.函数的值域是{0,1,2} B.函数是周期函数
C.函数的图象关于y轴对称 D.函数只有一个零点
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.若函数的两个零点是2和3,则不等式 的解集为________ .
14.某地为践行“绿水青山就是金山银山”的环保理念,大力展开植树造林.假设一片森林原来的面积为亩,计划每年种植一些树苗,且森林面积的年增长率相同,当面积是原来的2倍时,所用时间是10年.为使森林面积至少达到亩,至少需要植树造林______年(精确到整数).(参考数据:,)
15.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x()为二次函数的关系(如图),则每辆客车营运年数为________时,营运的年平均利润最大.
16.为了提高员工的工作积极性,某外贸公司想修订新的“员工激励计划”新的计划有以下几点需求:①奖金随着销售业绩的提高而提高;②销售业绩增加时,奖金增加的幅度逐渐上升;③必须和原来的计划接轨:销售业绩在10万元或以内时奖金为0,超过10万元则开始计算奖金,销售业绩为20万元时奖金为1千元.设业绩为x()万元时奖金为f(x)千元,下面给出三个函数模型:①;②;③.其中.请选择合适的函数模型,并计算:业绩为100万元时奖金为___________千元.
四、解答题
17.2021年12月9日15时40分,神舟十三号“天宫课堂”第一课开讲!受“天宫课堂”的激励与鼓舞,某同学对航天知识产生了浓厚的兴趣.通过查阅资料,他发现在不考虑气动阻力和地球引力等造成的影响时,火箭是目前唯一能使物体达到宇宙速度,克服或摆脱地 球引力,进人宇宙空间的运载工具.早在1903年齐奥尔科夫斯基就推导出单级火箭的最大理想速度公式: ,被称为齐奥尔科夫斯基公式,其中为发动机的喷射速度,和分别是火箭的初始质量和发动机熄火(推进剂用完 )时的质量.被称为火箭的质量比.
(1)某单级火箭的初始质量为160吨,发动机的喷射速度为2千米/秒,发动机熄火时的 质量为40吨,求该单级火箭的最大理想速度(保留2位有效数字);
(2)根据现在的科学水平,通常单级火箭的质量比不超过10.如果某单级火箭的发动机的喷射速度为2千米/秒,请判断该单级火箭的最大理想速度能否超过第一宇宙速度千米/秒,并说明理由.(参考数据:,无理数)
18.设,,若函数恰好有三个不同的零点,分别为 .
(1)求的取值范围;
(2)求的值.
19.对于函数,若在其定义域内存在实数,,使得成立,则称是“跃点”函数,并称是函数的1个“跃点”.
(1)求证:函数在上是“1跃点”函数;
(2)若函数在上存在2个“1跃点”,求实数的取值范围;
(3)是否同时存在实数和正整数使得函数在上有2022个“跃点”?若存在,请求出和满足的条件;若不存在,请说明理由.
20.某校数学兴趣小组,在过去一年一直在研究学校附近池塘里某种水生植物的面积变化情况,自2021年元旦开始测量该水生植物的面积,此后每隔一个月(每月月底)测量一次,通过一年的观察发现,自2021年元旦起,该水生植物在池塘里面积增加的速度是越来越快的.最初测得该水生植物面积为,二月底测得该水生植物的面积为,三月底测得该水生植物的面积为,该水生植物的面积y(单位:)与时间x(单位:月)的关系有两个函数模型可供选择,一个是同学甲提出的;另一个是同学乙提出的,记2021年元旦最初测量时间x的值为0.
(1)根据本学期所学,请你判断哪个同学提出的函数模型更适合?并求出该函数模型的解析式;
(2)池塘中该水生植物面积应该在几月份起是元旦开始研究时该水生植物面积的10倍以上?(参考数据:,)
21.我市某运输公司为积极响应国家节能减排的号召,年初以每台12800元的价格购入一批风能发电机.经测算,每台发电机每年的发电收益约7200元,已知每台发电机使用年后的累计维修保养费用为元,且满足关系式(,为常数).已知该批发电机第1年每台的维修保养费用为1000元,前2年每台的累计维修保养费用为2400元.设每台发电机使用年后的总利润为元.
(1)求关于的函数关系式;
(2)问每台发电机在第几年的年平均利润最大?(注:年平均利润总利润年数)
22.国际上常用恩格尔系数r来衡量一个国家或地区的人民生活水平.根据恩格尔系数的大小,可将各个国家或地区的生活水平依次划分为:贫困,温饱,小康,富裕,最富裕等五个级别,其划分标准如下表:
级别 贫困 温饱 小康 富裕 最富裕
标准 r>60% 50%<r≤60% 40%<r=50% 30%<r≤40% r≤30%
某地区每年底计算一次恩格尔系数,已知该地区2000年底的恩格尔系数为60%.统计资料表明:该地区食物支出金额年平均增长4%,总支出金额年平均增长.根据上述材料,回答以下问题.
(1)该地区在2010年底是否已经达到小康水平,说明理由;
(2)最快到哪一年底,该地区达到富裕水平?
参考数据:,,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
构造函数,分析函数在上的单调性,结合零点存在定理可得出结论.
【详解】
由可得,设,
因为函数、在上均为增函数,故函数在上也为增函数,
因为,,故.
故选:C.
2.C
【解析】
【分析】
结合函数的单调性,利用零点存在定理可判断出函数的零点所在的区间.
【详解】
∵函数,
∴函数在上单调递增,
又,,,
故函数的零点所在区间为.
故选:C.
3.B
【解析】
【分析】
设该商品每件的售价为x元,根据给定条件列出关于x的函数关系,借助函数最值求解作答.
【详解】
设该商品每件的售价为x元,则每件商品售出所获利润为元,销售量为件,
商场每天销售该商品所得的利润,
当时,(元),
所以该商品每件的售价为14元.
故选:B
4.A
【解析】
【分析】
根据题意列出剩留量和年份的关系式,结合对数的运算,即可求解.
【详解】
设该种放射性物质初始质量为,经过年,剩留量变为,
则可建立模型为,
即,
所以大约经过16年,该物质剩留的是原来的.
故选:A.
5.A
【解析】
【分析】
将问题转化为,,与交点的横坐标大小的比较,通过数形结合的方式可确定大小关系.
【详解】
在同一坐标系中分别作出,,,的图象,如图所示.
由图可知,函数,,的零点分别为,,,
则,,,所以.
故选:A
6.C
【解析】
【分析】
利用函数的单调性及零点存在定理即得.
【详解】
因为,
所以函数单调递减,
,
∴函数的零点所在区间为.
故选:C.
7.D
【解析】
【分析】
画出的图象,根据与的图象有个交点来求得的取值范围.
【详解】
当时,,的图象向右平移2个单位,
再把纵坐标变为原来的2倍,得到的图象,也即在区间上的图象.
以此类推,则在区间上的图象如图所示.
记,若方程恰好有四个实根,
则函数与 的图象有且只有四个公共点,
由图得,点,,,,则,,,,则,所以与的图象有且只有四个公共点时.
故选:D
8.C
【解析】
【分析】
利用条件得到,,从而求出x=21的函数值.
【详解】
函数中,当时,当时,
所以,则,所以当时,.
故选:C
9.AC
【解析】
【分析】
由零点存在性定理判断A选项,BD选项可以举出反例,C选项,得到在上的图象与轴没有交点,进而作出判断.
【详解】
由零点存在性定理可知:A正确;
如图1,满足,且存在实数,使得,故B错误;
因为对任意的实数,故在上的图象与轴没有交点,故在上的图象在x轴上方或在x轴下方,故,C正确;
如图1,存在实数,而,故D错误.
故选:AC
10.ACD
【解析】
【分析】
A.由偶函数在对称区间上的单调性判断;B.举例判断;C.由偶函数得到 ,再利用单调性判断;D. 由偶函数得到 ,再利用单调性求解判断;
【详解】
因为是定义在R上的偶函数,且在上单调递增,
所以在上单调递减,故A正确;
如,令,得或或,函数有三个零点,故B错误;
,因为,所以,故C正确;
若实数a满足,即,则,解得,故D正确;
故选:ACD
11.BCD
【解析】
【分析】
直接计算、的值,可判断A选项;利用函数在上的单调性可判断B选项;数形结合求出的取值范围,可判断C选项;求出不等式在时的解,数形结合可判断D选项的正误.
【详解】
对于A选项,,,故,A错;
对于B选项,当时,,此时函数单调递增,
当时,,此时函数单调递减,
因为,,,
且,,
,
因为,所以,,
即,所以,,
且,,,
所以,,
即,B对;
对于C选项,作出函数与的图象如下图所示:
由图可知,当时,直线与函数的图象至多有两个交点,不合乎题意,
当时,直线与函数的图象有无数个交点,不合乎题意,
由题意可知,直线与函数的图象有个交点,
则,解得,C对;
对于D选项,当时,由可得,解得,
当时,,结合图象可知当时,,D对.
故选:BCD.
12.ACD
【解析】
【分析】
先研究函数的奇偶性,作出函数的图象,作出函数的图象判断选项A、B、C的正确性,再分类讨论判断方程的根的个数得解.
【详解】
首先分析函数性质,为偶函数,故只需考虑x轴非负半轴图象;
时,,
所以图象如下:
因为,
所以也是偶函数,C正确;
从而只需考虑在x轴非负半轴图象;观察到在x轴非负半轴上的图象以为单位反复出现,故只需考虑 在上的图象;
决定取值的分界点是取整数的位置:
由,
,
,
得:,值域为,A正确;
作图象:
由图可知,图象在原点处的形状与左右两侧都不同,不是周期函数;故B错误;
,作直线,
观察图象得知,该直线所过定点,
恰好不在图象上,两条曲线只交于原点,故D正确.
故选:ACD.
13.
【解析】
【分析】
先根据根与系数的关系求出a,b,进而解出不等式即可.
【详解】
根据题意,,则不等式可化为.
故答案为:.
14.26.
【解析】
【分析】
先由已知求增长率,再求达到所需年数.
【详解】
设年增长率为,所求年数为,
根据已知:,解得,
又,所以,
至少需要植树造林26年.
故答案为:26.
15.5
【解析】
【分析】
首先根据题意得到二次函数的解析式为,再利用基本不等式求解的最大值即可.
【详解】
根据题意得到:抛物线的顶点为,过点,开口向下,
设二次函数的解析式为,
所以,解得,即,
则营运的年平均利润,
当且仅当,即时取等号.
故答案为:5.
16.
【解析】
【分析】
根据“销售业绩增加时,奖金增加的幅度逐渐上升”可知,给出的模型中只有满足,“必须和原来的计划接轨”表明,当时,,再结合“销售业绩为20万元时奖金为1千元”可知,当时,,然后解出方程即可
【详解】
根据题意,当时,给出三个函数模型均满足“奖金随着销售业绩的提高而提高”,而只有模型“”满足“销售业绩增加时,奖金增加的幅度逐渐上升”,故模型选择:
根据题意,则有:
解得:
则模型为:
当时,
故答案为:
17.(1)千米/秒;
(2)该单级火箭最大理想速度不可以超过第一宇宙速度千米/秒,理由见解析.
【解析】
【分析】
(1)由题可知,,,代入即求;
(2)利用条件可求,即得.
(1)
,,,
该单级火箭的最大理想速度为千米/秒.
(2)
,,
,
,
,
.
该单级火箭最大理想速度不可以超过第一宇宙速度千米/秒.
18.(1);
(2)。
【解析】
【分析】
(1)由函数与方程的关系转化为两个函数的交点问题,利用数形结合即得;
(2)根据三角函数的对称性,求出函数的对称轴,结合图象进行求解即可.
(1)
由得,
若函数恰好有三个不同的零点,等价于函数与的图象有三个交点,作出函数的图象如图,
由题知,则,
即的取值范围为.
(2)
由,得对称轴,
,由,解得,
当时,对称轴,时,对称轴,
由图象可知,点、关于直线对称,则,
点、关于直线对称,则,
因此,.
19.(1)证明见详解
(2)
(3)存在,或或
【解析】
【分析】
(1)将要证明问题转化为方程在上有解,构造函数转化为函数零点问题,结合零点存在性定理可证;
(2)原问题等价于方程在由两个根,然后构造二次函数,转化为零点分布问题可解;
(3)将问题转化为方程在上有2022个实数根,再转化为两个函数交点个数问题,然后可解.
(1)
因为
整理得,令,
因为,所以在区间有零点,即存在,使得,即存在,使得,
所以,函数在上是“1跃点”函数
(2)
函数在上存在2个“1跃点”方程在上有两个实数根,
即在上有两个实数根,
令,则
解得或,
所以的取值范围是
(3)
由,得,
即
因为函数在上有2022个“跃点”,所以方程在上有2022个解,即函数与的图象有2022个交点.
所以或或
即或或
20.(1)甲同学提出的函数模型满足要求,
(2)池塘中该水生植物面积应该在6月起是去年元旦开始研究时该水生植物面积的10倍以上
【解析】
【分析】
(1)根据水生植物面积的增长变化结合函数的增长变化快慢选择即可;
(2)根据题意建立不等式,利用取对数的方法求解即可.
(1)
因为两个函数模型,在上都是增函数.
随着x的增大,的函数值增加的越来越快,而的函数值增加的越来越慢.
因为在池塘里该水生植物蔓延的速度是越来越快,即随着时间增加,该水生植物的面积增加的越来越快,
所以,甲同学提出的函数模型满足要求.
由题意知,解得,,
所以,
(2)
一月底水深植物面积为
由,解得
又
故.
所以,池塘中该水生植物面积应该在6月起是去年元旦开始研究时该水生植物面积的10倍以上.
21.(1),
(2)第8年的年平均利润最大.
【解析】
【分析】
(1)首先根据题意得到,解方程组得到,再根据题意即可得到函数的解析式.
(2)利用基本不等式求解即可.
(1)
由题知:,解得,
所以.
,.
(2)
设平均利润,所以,
所以.
当且仅当,即时取等号.
所以每台发电机在第8年的年平均利润最大.
22.(1)已经达到,理由见解析
(2)2022年
【解析】
【分析】
(1)根据该地区食物支出金额年平均增长4%,总支出金额年平均增长的比例列式求解,判断十年后是否达到即可.
(2)假设经过n年,该地区达到富裕水平,列式,利用指对数互化解不等式即可.
(1)
该地区2000年底的恩格尔系数为%,
则2010年底的思格尔系数为
因为
所以1,
则
所以.
所以该地区在2010年底已经达到小康水平.
(2)
从2000年底算起,设经过n年,该地区达到富裕水平
则,
故,即.
化为.
因为,则In,所以.
因为
.
所以.
所以,最快到2022年底,该地区达到富裕水平.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
