苏科版七年级数学下册 9.4 乘法公式 课件(共20张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 9.4 乘法公式 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 181.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
9.4 乘法公式
灰太狼开了租地公司,他把一边长为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,大家一听,都说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…同学们,你能告诉慢羊羊这是为什么吗
乘法公式(2)
——平方差公式
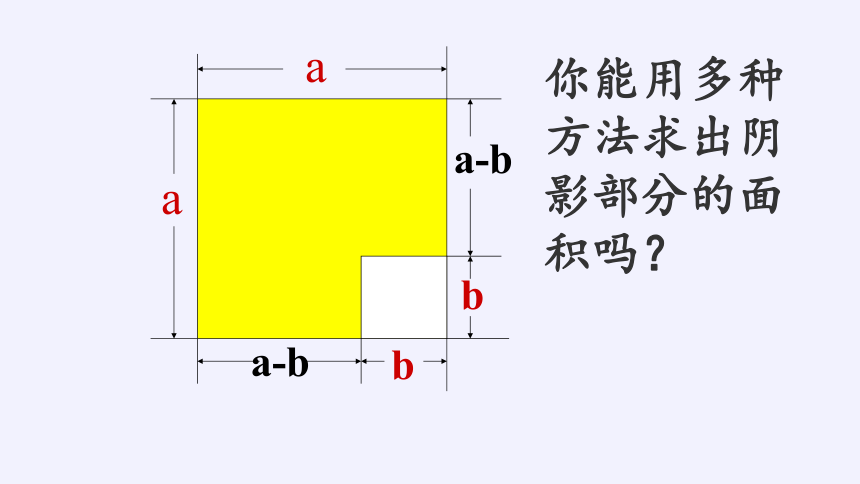
a
a
b
b
a-b
a-b
你能用多种方法求出阴影部分的面积吗?
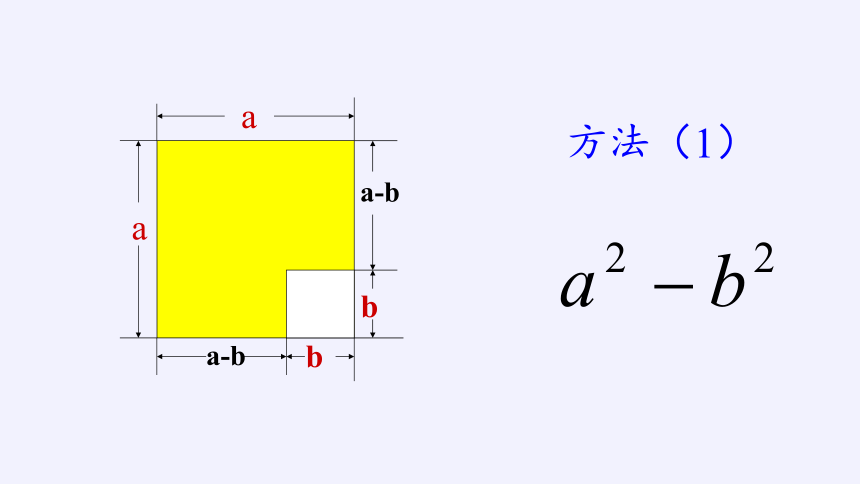
方法(1)
a
a-b
a-b
a
b
b
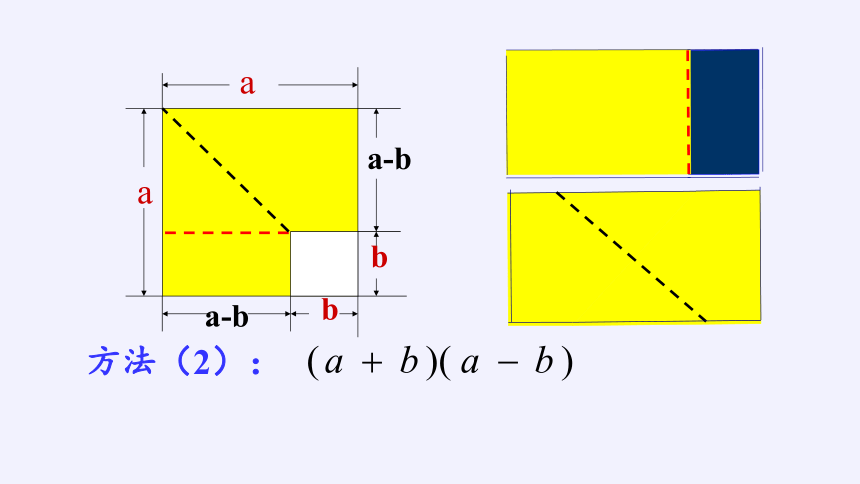
方法(2):
a
b
b
a-b
a-b
a
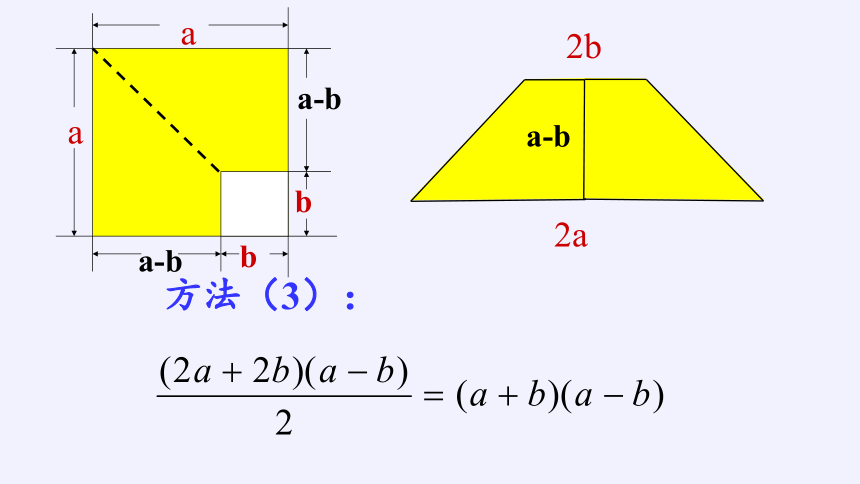
方法(3):
2a
b
a-b
a-b
a
b
2b
a
a-b
证明:(a+b)(a-b)
我们将这个公式叫做平方差公式.
(合并同类项)
即: (a+b)(a-b)
从代数角度出发,我们一起来进行验证.
平方差公式
两数和与这两数差的积,等于它们的平方差.
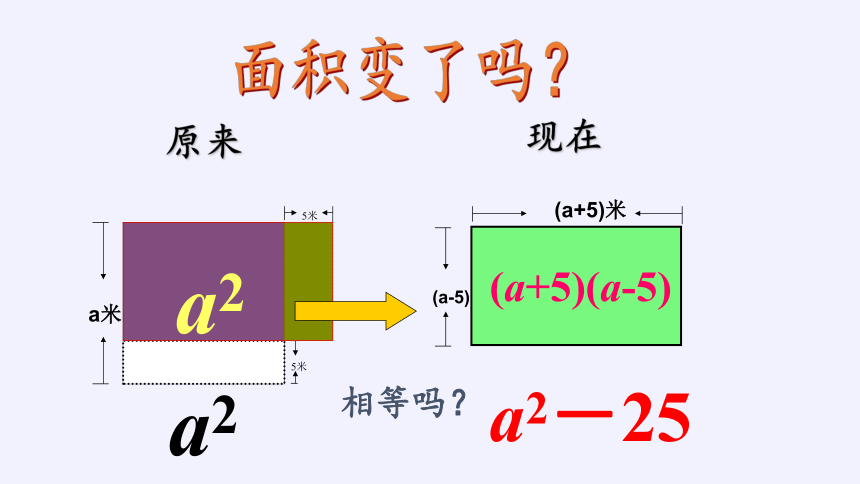
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
面积变了吗?
a2
(a+5)(a-5)
a2
a2-25
(a+b)(a b)=
a2 b2
结构特点
(1)左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数(式)
(2)右边是乘式中两项的平方差,即(相同项)2 (相反项)2
注意:字母a、b的代表性
a、b可以是一个数字,
也可以是一个单项式或多项式
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(-y 2x).
(不能)
(1)下列式子可用平方差公式计算吗 为什么 如果能够,请用计算出结果
(不能)
(不能)
(能)
(a2 b2)=
(能) ( 2x)2-y2=4x2-y2
a2 + b2
例1
注 :运用平方差公式必须具备的条件
两个二项式相乘,有一项完全相同;
另一项互为相反数(式)
(a+b)(a-b) a b a2-b2 最后结果
(2x+3y)(2x-3y)
(-2x+3y)(2x+3y)
(-2x-3y)(2x-3y)
2x
3y
(2x)2-(3y)2
4x2-9y2
2.填一填
3y
2x
(3y)2-(2x)2
9y2- 4x2
-3y
2x
(-3y)2-(2x)2
9y2- 4x2
思考:利用平方差公式计算的关键是____________________
怎样确定a与b____________________________
准确确定a和b
符号相同的项是a,符号相反的项是b
例2、运用平方差公式计算:
(1)(5x+y)(5x-y)
(3)(-x+3y)(-x-3y)
(4)(-2x-y)(2x-y)
运用平方差公式时要注意:
.先判断,找出题中的a与b,
.结果是平方差,
顺序不要颠倒
.注意系数指数的变化
例3.在下列括号内填上合适的整式
(______)(3m+5n)=9m2-25n2
(-2a-5b)(______)=4a2-25b2
(______)(5a+1)=1-25a2
(7x2-3y2)(3y2+____)=49x4-____
关键:从已知项中分析得出
相同项和相反项
3m-5n
-2a+5b
1-5a
7x2
9y4
喜羊羊同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,喜羊羊就说出应99.96元,结果与售货员计算出的结果相吻合。
售货员很惊讶地说:“你真是个神童,怎么算得这么快?”
喜羊羊同学说:“过奖了,我利用了在数学上刚学过的一个公式。”
生活数学
练一练
20042-2003×2005
例4、用平方差公式计算:
103×97
(1) (x-y)(x+y)(x2+y2)
(2)
(3)(a-b+c)(a+b-c)
(4)(a-b+c)(a-b-c)
1、利用平方差公式计算
思维延伸
小结:注意实质,善用变形创造条件应用平方差公式
2.美羊羊同学在计算(2+1)(22+1)(24+1)时,将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能从她的做法得到启发求出(3+1)(32+1)(34+1)的值吗?
思维延伸
这节课你学到了什么?
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
谢 谢
9.4 乘法公式
灰太狼开了租地公司,他把一边长为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,大家一听,都说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…同学们,你能告诉慢羊羊这是为什么吗
乘法公式(2)
——平方差公式
a
a
b
b
a-b
a-b
你能用多种方法求出阴影部分的面积吗?
方法(1)
a
a-b
a-b
a
b
b
方法(2):
a
b
b
a-b
a-b
a
方法(3):
2a
b
a-b
a-b
a
b
2b
a
a-b
证明:(a+b)(a-b)
我们将这个公式叫做平方差公式.
(合并同类项)
即: (a+b)(a-b)
从代数角度出发,我们一起来进行验证.
平方差公式
两数和与这两数差的积,等于它们的平方差.
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
面积变了吗?
a2
(a+5)(a-5)
a2
a2-25
(a+b)(a b)=
a2 b2
结构特点
(1)左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数(式)
(2)右边是乘式中两项的平方差,即(相同项)2 (相反项)2
注意:字母a、b的代表性
a、b可以是一个数字,
也可以是一个单项式或多项式
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(-y 2x).
(不能)
(1)下列式子可用平方差公式计算吗 为什么 如果能够,请用计算出结果
(不能)
(不能)
(能)
(a2 b2)=
(能) ( 2x)2-y2=4x2-y2
a2 + b2
例1
注 :运用平方差公式必须具备的条件
两个二项式相乘,有一项完全相同;
另一项互为相反数(式)
(a+b)(a-b) a b a2-b2 最后结果
(2x+3y)(2x-3y)
(-2x+3y)(2x+3y)
(-2x-3y)(2x-3y)
2x
3y
(2x)2-(3y)2
4x2-9y2
2.填一填
3y
2x
(3y)2-(2x)2
9y2- 4x2
-3y
2x
(-3y)2-(2x)2
9y2- 4x2
思考:利用平方差公式计算的关键是____________________
怎样确定a与b____________________________
准确确定a和b
符号相同的项是a,符号相反的项是b
例2、运用平方差公式计算:
(1)(5x+y)(5x-y)
(3)(-x+3y)(-x-3y)
(4)(-2x-y)(2x-y)
运用平方差公式时要注意:
.先判断,找出题中的a与b,
.结果是平方差,
顺序不要颠倒
.注意系数指数的变化
例3.在下列括号内填上合适的整式
(______)(3m+5n)=9m2-25n2
(-2a-5b)(______)=4a2-25b2
(______)(5a+1)=1-25a2
(7x2-3y2)(3y2+____)=49x4-____
关键:从已知项中分析得出
相同项和相反项
3m-5n
-2a+5b
1-5a
7x2
9y4
喜羊羊同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,喜羊羊就说出应99.96元,结果与售货员计算出的结果相吻合。
售货员很惊讶地说:“你真是个神童,怎么算得这么快?”
喜羊羊同学说:“过奖了,我利用了在数学上刚学过的一个公式。”
生活数学
练一练
20042-2003×2005
例4、用平方差公式计算:
103×97
(1) (x-y)(x+y)(x2+y2)
(2)
(3)(a-b+c)(a+b-c)
(4)(a-b+c)(a-b-c)
1、利用平方差公式计算
思维延伸
小结:注意实质,善用变形创造条件应用平方差公式
2.美羊羊同学在计算(2+1)(22+1)(24+1)时,将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能从她的做法得到启发求出(3+1)(32+1)(34+1)的值吗?
思维延伸
这节课你学到了什么?
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
