2021-2022学年华东师大版七年级下册数学第九章不等式与不等式组小结与复习(第一课时)课件(20张)
文档属性
| 名称 | 2021-2022学年华东师大版七年级下册数学第九章不等式与不等式组小结与复习(第一课时)课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 10:16:31 | ||
图片预览




文档简介
(共20张PPT)
第九章
不等式与不等式组
小结与复习(第一课时)
人教版数学七年级下册
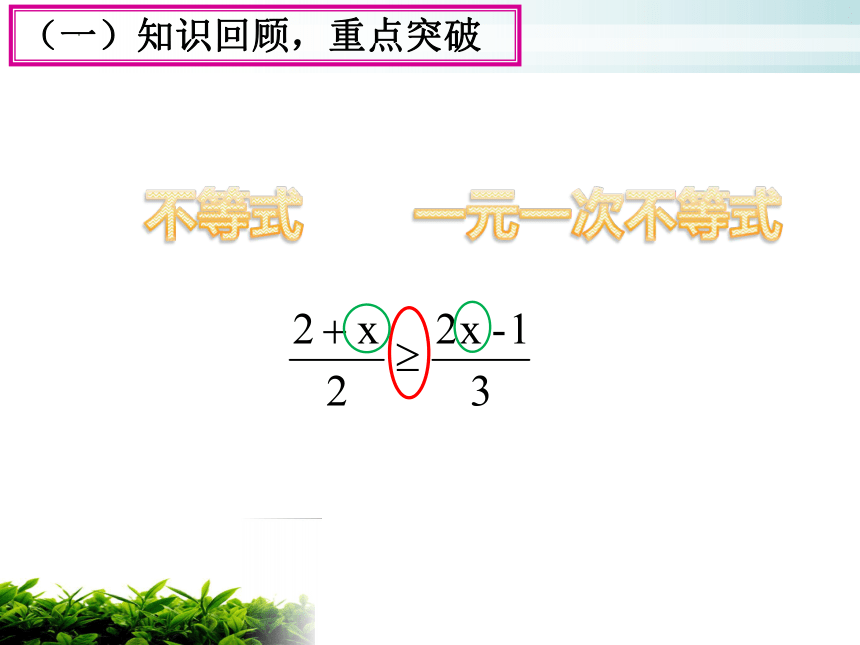
一元一次不等式
不等式
(一)知识回顾,重点突破
不等式的性质3:不等式的两边乘(或除以)同一个负数, 不等号的方向改变.
不等式的性质1:不等式的两边加(或减)同一个数(或式 子),不等号的方向不变.
不等式的性质2:不等式的两边乘(或除以)同一个正数, 不等号的方向不变.
不等式的性质
(一)知识回顾,重点突破
例1
(1)若x>y,则x+3 y+3 ;
依据: .
(2) 若am<bm,则a>b,则m 0;
依据: .
(3) 若a<b,则2-a 2-b;
依据: .
>
不等式的性质1
<
不等式的性质3
>
不等式的性质3、不等式的性质1
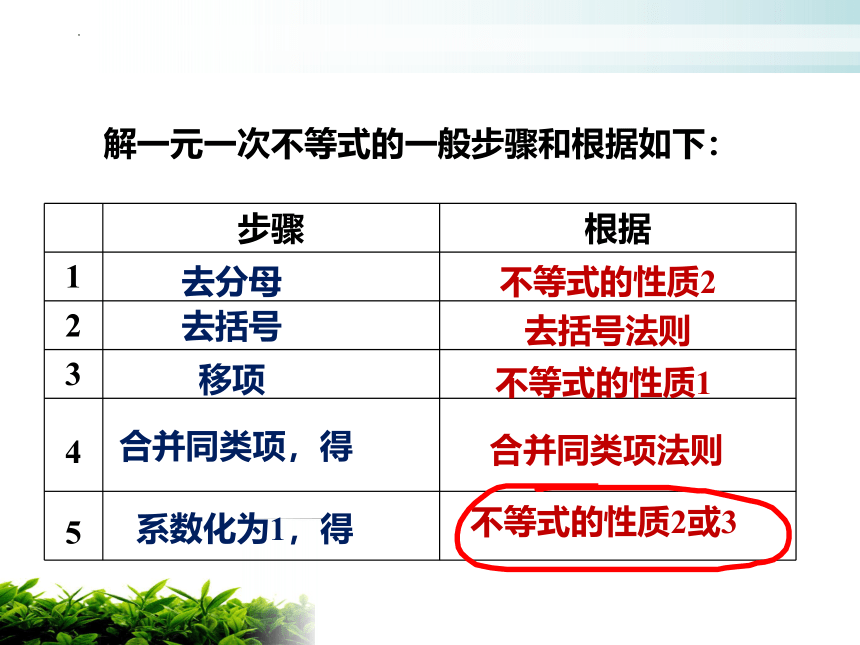
解一元一次不等式的一般步骤和根据如下:
步骤 根据
1
2
3
4
5
去分母
去括号
移项
合并同类项,得
不等式的性质2
去括号法则
合并同类项法则
不等式的性质2或3
不等式的性质1
系数化为1,得
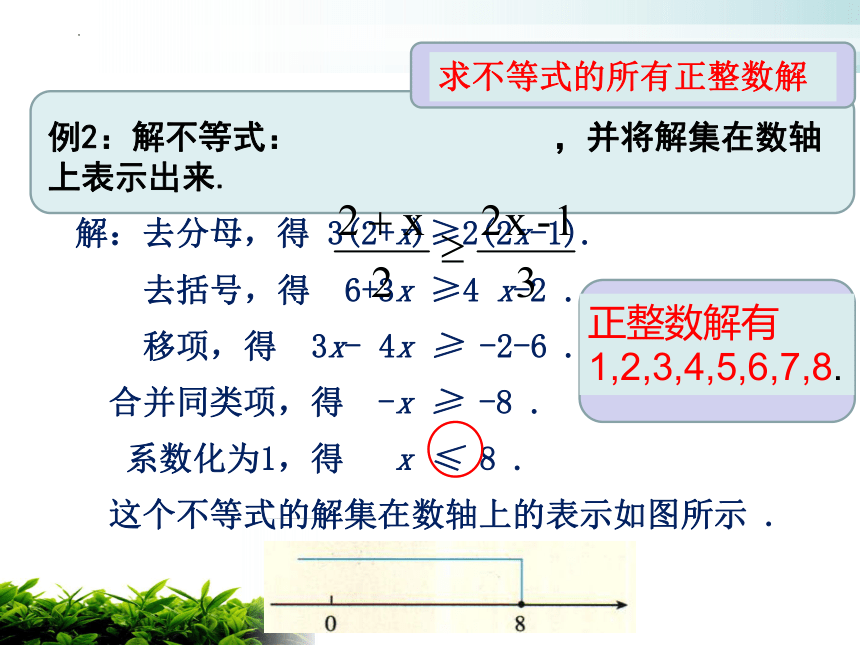
解:去分母,得 3(2+x)≥2(2x-1).
去括号,得 6+3x ≥4 x-2 .
移项,得 3x- 4x ≥ -2-6 .
合并同类项,得 -x ≥ -8 .
系数化为1,得 x ≤ 8 .
这个不等式的解集在数轴上的表示如图所示 .
例2:解不等式: ,并将解集在数轴上表示出来.
求不等式的所有正整数解
正整数解有1,2,3,4,5,6,7,8.
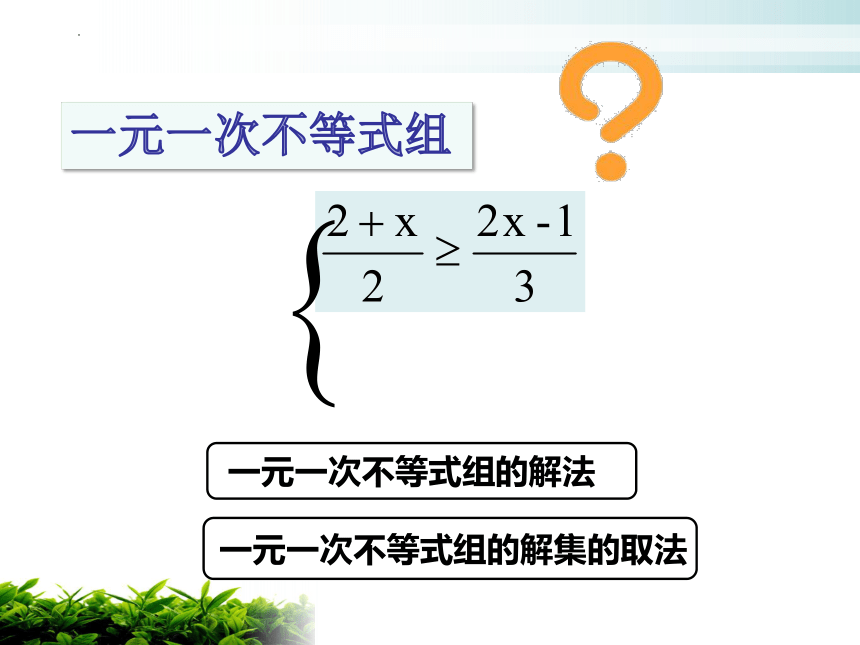
一元一次不等式组
一元一次不等式组的解法
一元一次不等式组的解集的取法
不等式组 图示 解集
(a>b)
无解
一元一次不等式组的解集的取法
数形结合
分别求
画数轴
确定解集
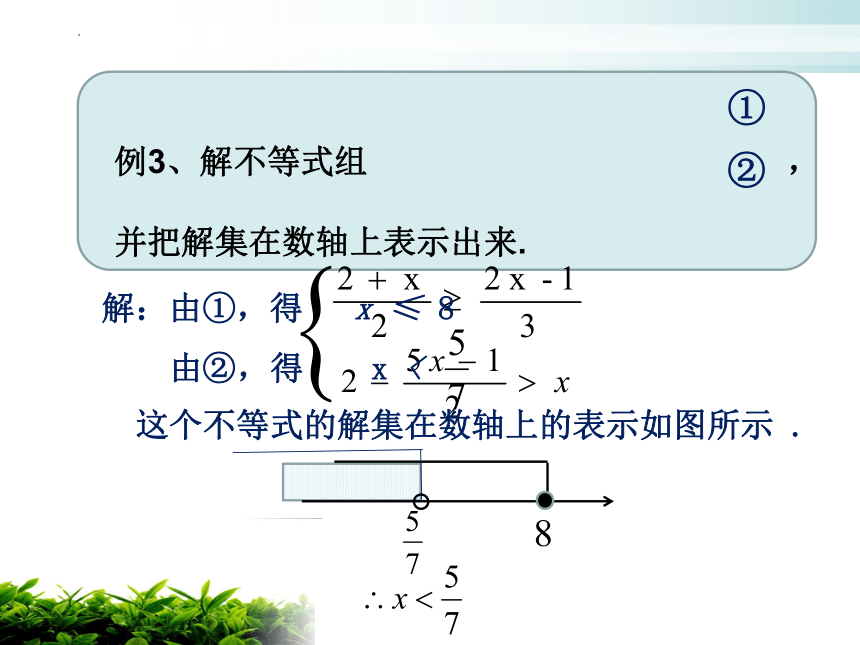
例3、解不等式组 ,
并把解集在数轴上表示出来.
解:由①,得 x ≤ 8
由②,得 x <
这个不等式的解集在数轴上的表示如图所示 .
①
②
a
含参数的一元一次不等式
对于含参数的不等式的问题你会求吗?
(二)灵活应用,拓展延伸
例4:关于x的不等式 ,
的解集为 ,求a的值.
含参数的一元一次不等式组
对于含参数的不等式组的问题,你会求吗?
解:由①,得 x ≤3a+2
由②,得 x <
又∵不等式组的解集为x ≤3a+2
∴3a+2<
∴a<
例5、关于x的不等式组:
的解集为x ,求a的取值范围
①
②
不等式
不等式
不等式组
概念:
不等式与不等式组
一元一次
不等式
解集:
解法:
概念:
解,解集:
性质:
概念:
解法:
一元一次
不等式组
2.不等式组 的解集在数轴上表示正确的是( )
3.在平面直角坐标系中,若点P(m-3,m+1)在第二象限,则m的取值范围为( )
A.-1<m<3 B.m>3 C.m<-1 D.m>-1
(三)交流反馈,易错强化
1.由(a-1)x>1,得到 ,则a的取值范围是 .
A
A
a<1
4、解不等式 ,并把解集在数轴上表示出来.
5.解不等式组 ,并求出其整数解.
(三)交流反馈,易错强化
答案:x≥2
≤
答案:-1 x<5
整数解为:-1、0、1、2、3、4.
6、不等式组 的解集是x>2,求m的
取值范围.
解:由①,得 x >2
由②,得 x >m+1
又∵不等式组的解集为x >2
m≤1
∴m+1≤2
m≤1
(四)总结反思,共同提高
1、通过本节课的复习,你都有哪些收获?.
2、结合你自己的复习情况,谈谈你还有什么疑问
不等式
不等式
不等式组
概念:
不等式与不等式组
一元一次
不等式
解集:
解法:
概念:
解,解集:
性质:
概念:
解法:
一元一次
不等式组
人的一生,有得有失。就像跷跷板,有时高,也有时低。勤勉读书的我们,可能会少了一些和伙伴玩耍的时间,少了一些做自己喜欢事情的时间,但我们要坚信,失之东隅收之桑榆,只要我们努力学习,失去的都将会以另一种方式回归。
(五)课后作业
必做题:课本P133页复习题9的3、4题 ;
选做题:已知不等式组 的解集中
共有5个整数,求a的取值范围.
第九章
不等式与不等式组
小结与复习(第一课时)
人教版数学七年级下册
一元一次不等式
不等式
(一)知识回顾,重点突破
不等式的性质3:不等式的两边乘(或除以)同一个负数, 不等号的方向改变.
不等式的性质1:不等式的两边加(或减)同一个数(或式 子),不等号的方向不变.
不等式的性质2:不等式的两边乘(或除以)同一个正数, 不等号的方向不变.
不等式的性质
(一)知识回顾,重点突破
例1
(1)若x>y,则x+3 y+3 ;
依据: .
(2) 若am<bm,则a>b,则m 0;
依据: .
(3) 若a<b,则2-a 2-b;
依据: .
>
不等式的性质1
<
不等式的性质3
>
不等式的性质3、不等式的性质1
解一元一次不等式的一般步骤和根据如下:
步骤 根据
1
2
3
4
5
去分母
去括号
移项
合并同类项,得
不等式的性质2
去括号法则
合并同类项法则
不等式的性质2或3
不等式的性质1
系数化为1,得
解:去分母,得 3(2+x)≥2(2x-1).
去括号,得 6+3x ≥4 x-2 .
移项,得 3x- 4x ≥ -2-6 .
合并同类项,得 -x ≥ -8 .
系数化为1,得 x ≤ 8 .
这个不等式的解集在数轴上的表示如图所示 .
例2:解不等式: ,并将解集在数轴上表示出来.
求不等式的所有正整数解
正整数解有1,2,3,4,5,6,7,8.
一元一次不等式组
一元一次不等式组的解法
一元一次不等式组的解集的取法
不等式组 图示 解集
(a>b)
无解
一元一次不等式组的解集的取法
数形结合
分别求
画数轴
确定解集
例3、解不等式组 ,
并把解集在数轴上表示出来.
解:由①,得 x ≤ 8
由②,得 x <
这个不等式的解集在数轴上的表示如图所示 .
①
②
a
含参数的一元一次不等式
对于含参数的不等式的问题你会求吗?
(二)灵活应用,拓展延伸
例4:关于x的不等式 ,
的解集为 ,求a的值.
含参数的一元一次不等式组
对于含参数的不等式组的问题,你会求吗?
解:由①,得 x ≤3a+2
由②,得 x <
又∵不等式组的解集为x ≤3a+2
∴3a+2<
∴a<
例5、关于x的不等式组:
的解集为x ,求a的取值范围
①
②
不等式
不等式
不等式组
概念:
不等式与不等式组
一元一次
不等式
解集:
解法:
概念:
解,解集:
性质:
概念:
解法:
一元一次
不等式组
2.不等式组 的解集在数轴上表示正确的是( )
3.在平面直角坐标系中,若点P(m-3,m+1)在第二象限,则m的取值范围为( )
A.-1<m<3 B.m>3 C.m<-1 D.m>-1
(三)交流反馈,易错强化
1.由(a-1)x>1,得到 ,则a的取值范围是 .
A
A
a<1
4、解不等式 ,并把解集在数轴上表示出来.
5.解不等式组 ,并求出其整数解.
(三)交流反馈,易错强化
答案:x≥2
≤
答案:-1 x<5
整数解为:-1、0、1、2、3、4.
6、不等式组 的解集是x>2,求m的
取值范围.
解:由①,得 x >2
由②,得 x >m+1
又∵不等式组的解集为x >2
m≤1
∴m+1≤2
m≤1
(四)总结反思,共同提高
1、通过本节课的复习,你都有哪些收获?.
2、结合你自己的复习情况,谈谈你还有什么疑问
不等式
不等式
不等式组
概念:
不等式与不等式组
一元一次
不等式
解集:
解法:
概念:
解,解集:
性质:
概念:
解法:
一元一次
不等式组
人的一生,有得有失。就像跷跷板,有时高,也有时低。勤勉读书的我们,可能会少了一些和伙伴玩耍的时间,少了一些做自己喜欢事情的时间,但我们要坚信,失之东隅收之桑榆,只要我们努力学习,失去的都将会以另一种方式回归。
(五)课后作业
必做题:课本P133页复习题9的3、4题 ;
选做题:已知不等式组 的解集中
共有5个整数,求a的取值范围.
