2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元整合练习题(培优)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元整合练习题(培优)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 10:28:49 | ||
图片预览



文档简介
第7章 平面图形的认识(二) 单元整合练习题(培优)
2021-2022学年苏科版七年级数学下册
一、选择题
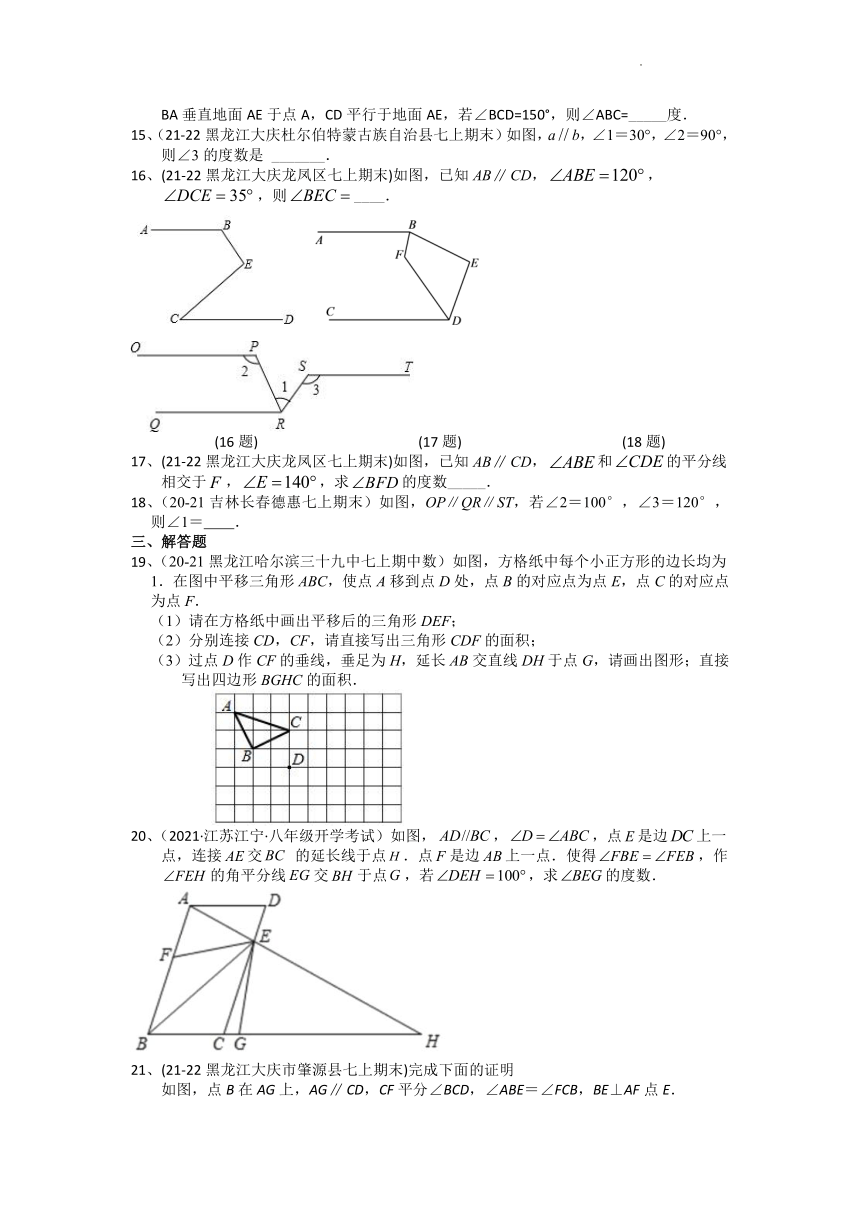
1、(21-22黑龙江哈尔滨市香坊区七上期末) 在如图中,∠1和∠2不是同位角的是( )
A. B. C. D.
2、下列车标图案,可以看成由图形的平移得到的是( )
A.B. C.D.
3、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A. 第一次向左拐30°,第二次向右拐30° B. 第一次向左拐45°,第二次向左拐45°
C. 第一次向左拐60°,第二次向右拐120° D. 第一次向左拐53°,第二次向左拐127°
4、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,已知,, ,则 的度数为( )
A. 50° B. 55° C. 45° D. 60°
(4题) (5题) (6题)
5、(2019秋 奈曼旗期末)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,试着找一找这个规律,你发现的规律是( )
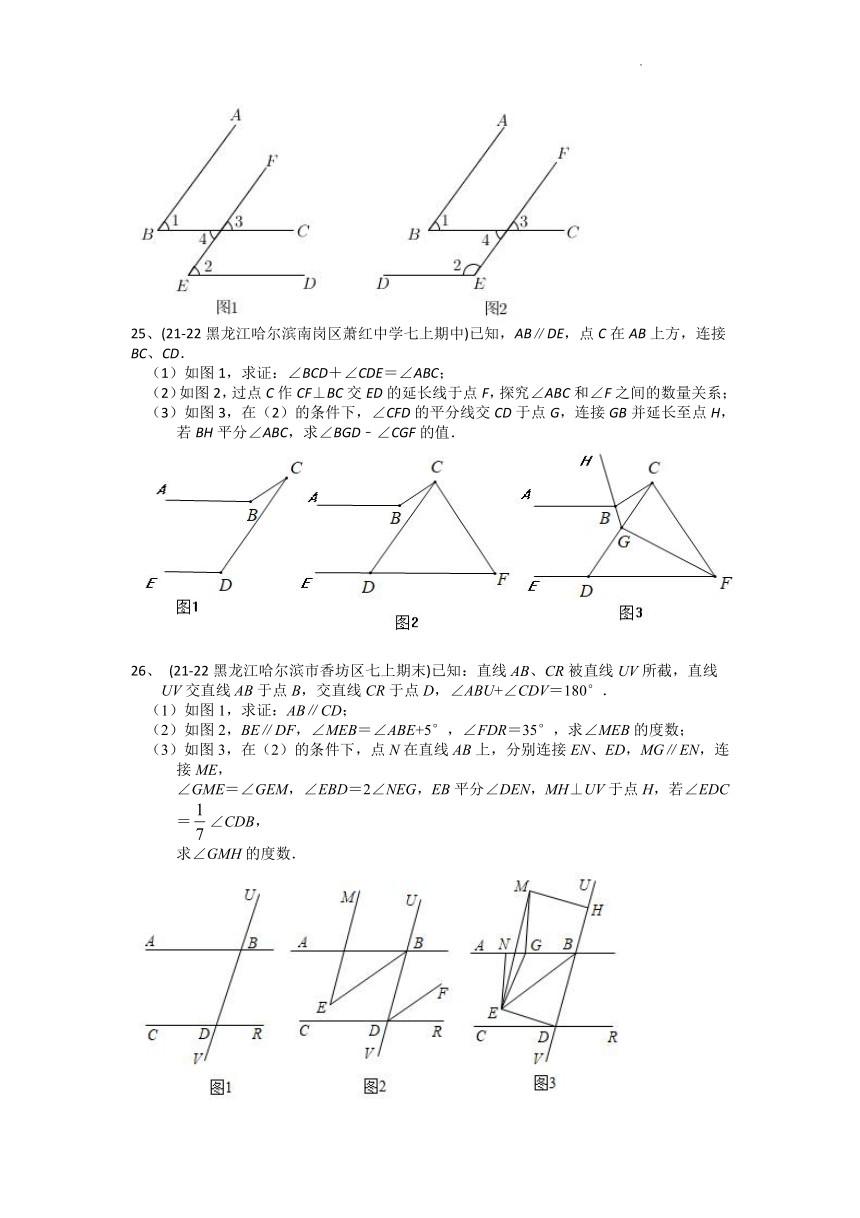
A.∠1+∠2=2∠A B.∠1+∠2=∠A C.∠A=2(∠1+∠2) D.∠1+∠2=∠A
6、(21-22黑龙江大庆市龙凤区上期中)如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( )
A. 85° B. 95° C. 90° D. 80°
7、(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
(7题) (8题) (9题)
8、(20-21黑龙江哈尔滨三十九中七上期中)如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个 B.6个 C.7个 D.8个
9、(21-22黑龙江哈尔滨市香坊区七上期末)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,∠EAB=72°,以下四个说法:①∠CDF=30°;②∠ADB=50°;③∠ABD=22°;④∠CBN=108°
其中正确说法的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
10、(2018·四川达州市·七年级期末)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 =___________.
(10题) (11题) (12题)
二、填空题
11、(2021春 鹿城区校级月考)如图,平移图形M,使其与图形N可以拼成一个平行四边形,则图中α的度数是 .
12、(21-22黑龙江哈尔滨市第六十九中学校七上期末)如图所示,将三角形纸片沿DE折叠,使点C落在点C ′处,若EC′恰好与BC平行,且∠C=80°,则∠BDE=_____.
13、(20-21黑龙江哈尔滨三十九中七上期中数)如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC= °.
(13题) (14题) (15题)
14、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
15、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,ab,∠1=30°,∠2=90°,则∠3的度数是 _______.
16、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,,,则____.
(16题) (17题) (18题)
17、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,和的平分线相交于,,求的度数_____.
18、(20-21吉林长春德惠七上期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
三、解答题
19、(20-21黑龙江哈尔滨三十九中七上期中数)如图,方格纸中每个小正方形的边长均为1.在图中平移三角形ABC,使点A移到点D处,点B的对应点为点E,点C的对应点为点F.
(1)请在方格纸中画出平移后的三角形DEF;
(2)分别连接CD,CF,请直接写出三角形CDF的面积;
(3)过点D作CF的垂线,垂足为H,延长AB交直线DH于点G,请画出图形;直接写出四边形BGHC的面积.
20、(2021·江苏江宁·八年级开学考试)如图,,,点是边上一点,连接交 的延长线于点.点是边上一点.使得,作的角平分线交于点,若,求的度数.
21、(21-22黑龙江大庆市肇源县七上期末)完成下面的证明
如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD(___________________)
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD(__________________)
∴________=∠BCF(等量代换)
∴BECF(______________________)
∴________=∠F(_________________)
∵BE⊥AF(已知)
∴________=90°(___________________)
∴∠F=90°.
22、(21-22黑龙江哈尔滨南岗区萧红中学七上期中(人教五四))如图,在三角形ABC中,D,E,F分别是三边上点,且DE平分∠ADF,∠ADF=2∠DFB.
(1)判断DE与BC是否平行,并说明理由.
(2)若EF∥AB,∠DFE=3∠CFE,求∠ADE度数.
23、(21-22黑龙江大庆市龙凤区上期中)已知:如图,EF∥CD,.
(1)判断与的位置关系,并说明理由.
(2)若平分,平分,且,求的度数.
24、(21-22黑龙江大庆市龙凤区上期中)已知一个角的两边与另一个角的两边分别平行,分别结合下图,试探索这两个角的关系,并证明你的结论.
(1)如图1,AB∥EF,BC∥DE,与的关系是_____.
(2)如图2,AB∥EF,BC∥DE,与的关系是________________.
(3)经过上述证明,我们可以得到一个结论:
(4)若两个角的两边分别平行,且一个角比另一个角的倍少,则这两个角分别是多少度?
25、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
26、 (21-22黑龙江哈尔滨市香坊区七上期末)已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,
∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,
求∠GMH的度数.
第7章 平面图形的认识(二) 单元整合练习题(培优)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、(21-22黑龙江哈尔滨市香坊区七上期末) 在如图中,∠1和∠2不是同位角的是( )
A. B. C. D.
【答案】D
【解析】
【分析】本题题考查三线八角中的同位角识别,解题关键在于掌握判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
同位角的定义:两条直线a,b被第三条直线c所截,在截线c的同侧,被截两直线a,b的同一方向的两个角,我们把这样的两个角称为同位角,依此即可求解.
【详解】解:A、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D、∠1与∠2的一边不在同一条直线上,不是同位角,符合题意.
故选:D.
2、下列车标图案,可以看成由图形的平移得到的是( )
A.B. C.D.
【分析】根据旋转变换,平移变换,轴对称变换对各选项分析判断后利用排除法求解.
【解答】解:A、可以由一个“基本图案”平移得到,故本选项符合题意;
B、不是由一个“基本图案”平移得到,故本选项不符合题意;
C、可以由一个“基本图案”旋转得到,故本选项不符合题意;
D、可以由一个“基本图案”旋转得到,故本选项不符合题意.
故选:A.
3、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A. 第一次向左拐30°,第二次向右拐30° B. 第一次向左拐45°,第二次向左拐45°
C. 第一次向左拐60°,第二次向右拐120° D. 第一次向左拐53°,第二次向左拐127°
【答案】D
【分析】本题考查了角的和差计算,正负数用表示生活中的角度的实际应用,理解角度和的意义,将所求问题转化为数学问题是解题关键.
根据规定向左拐的角度为正,向右拐的角度为负,两角之和为0°,与原方向相同,两角之和为90°,与原方向垂直,两角之和为180°,与原方向相反,找出两次拐弯的角度的和为即可得.
【详解】解:由题意,规定向左拐的角度为正,向右拐的角度为负,
A、第一次向左拐30°用+30°表示,第二次向右拐30°用-30°表示,∵,∴两次拐弯后的行驶方向与原来的方向相同,此项不符题意;
B、第一次向左拐45°用+45°表示,第二次向左拐45°用-45°表示,∵,∴两次拐弯后的行驶方向与原来的方向相同,此项不符题意;
C、第一次向左拐60°用+60°表示,第二次向右拐120°用-120°表示,∵,∴两次拐弯后的行驶方向与原来的方向成角,此项不符题意;
D、第一次向左拐53°用+53°表示,第二次向左拐127°用+127°表示,∵,∴两次拐弯后的行驶方向与原来的方向相反,此项符合题意;
故选:D.
4、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,已知,, ,则 的度数为( )
A. 50° B. 55° C. 45° D. 60°
【答案】B
【分析】本题考查了平行线的性质,三角形的内角和定理,外角的性质,熟悉相关性质是解题的关键.依据,得到,再根据,,即可得到,可得出.
详解】解:,
,
又,,
∴=,
故选:.
5、(2019秋 奈曼旗期末)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,试着找一找这个规律,你发现的规律是( )
A.∠1+∠2=2∠A B.∠1+∠2=∠A
C.∠A=2(∠1+∠2) D.∠1+∠2=∠A
【分析】本题考查了折叠的性质和三角形的内角和定理的应用,关键是得出等式∠ADE=90°-∠1,∠AED=90°-∠2,∠A=180°﹣(∠AED+∠ADE).
根据折叠得出∠ADE=∠A′DE,∠AED=∠A′ED,求出2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,推出∠ADE=90°-∠1,∠AED=90°-∠2,在△ADE中,∠A=180°﹣(∠AED+∠ADE),代入求出即可.
【解答】解:如图,延长BD和CE交于A′,
∵把△ABC沿DE折叠,当点A落在四边形BCDE内部,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,
∴∠ADE=90°-∠1,∠AED=90°-∠2,
∵在△ADE中,∠A=180°﹣(∠AED+∠ADE),
∴∠A=∠1+∠2,即2∠A=∠1+∠2.
故选:A.
6、(21-22黑龙江大庆市龙凤区上期中)如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( )
A. 85° B. 95° C. 90° D. 80°
【答案】B
【分析】本题主要考查翻折变换的知识,解答本题的关键是熟练掌握解题过程中应注意折叠前后的对应关系.
根据折叠前后图形全等和平行线,先求出∠CPR和∠CRP,再根据三角形内角和定理即可求出∠C.
【详解】因为折叠前后两个图形全等,C′P∥AB,C′R∥AD
∴∠CPR=∠C′PC =∠B=×120°=60°,
∠CRP=∠C′RC =∠D=×50°=25°;
∴∠C=180° 25° 60°=95°
故选:B.
7、(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
【答案】C
解:∵F是EC的中点,
∴,
∴,
∵ E是BD的中点 ,
∴,,
∵,
∴,
∴,
故选:C.
8、(20-21黑龙江哈尔滨三十九中七上期中)如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个 B.6个 C.7个 D.8个
【分析】依据平行线的性质,即可得到图中与∠B相等的角的个数.
【解答】解:∵AC∥DE,AB∥DF,
∴∠C=∠BDE,∠B=∠CDF,
又∵∠B=∠C,
∴∠C=∠BDE=∠B=∠CDF,
∵EF∥BC,
∴∠DEF=∠BDE,∠DFE=∠CDF,∠AEF=∠B,∠AFE=∠C,
∴与∠B相等的角为:∠BDE,∠CDF,∠C,∠DEF,∠DFE,∠AEF,∠AFE,
∴图中与∠B相等的角(∠B除外)有7个,
故选:C.
9、(21-22黑龙江哈尔滨市香坊区七上期末)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,∠EAB=72°,以下四个说法:①∠CDF=30°;②∠ADB=50°;③∠ABD=22°;④∠CBN=108°
其中正确说法的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【分析】本题考查平行线性质,角的倍分,邻补角性质,三角形内角和,一元一次方程,掌握平行线性质,邻补角性质,三角形内角和,一元一次方程地解题关键.
根据AD∥BC,∠C=30°,利用内错角相等得出∠FDC=∠C=30°,可判断①正确;根据邻补角性质可求∠ADC=180°-∠FDC=180°-30°=150°,根据∠ADB:∠BDC=1:2,得出方程3∠ADB=150°,解方程可判断②正确;根据∠EAB=72°,可求邻补角∠DAN=180°-∠EAB=180°-72°=108°,利用三角形内角和可求∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°可判断③正确,利用AD∥BC,同位角相等的∠CBN=∠DAN=108°可判断④正确即可.
【详解】解:∵AD∥BC,∠C=30°,∴∠FDC=∠C=30°,故①正确;
∴∠ADC=180°-∠FDC=180°-30°=150°,
∵∠ADB:∠BDC=1:2,∴∠BDC=2∠ADB,
∵∠ADC=∠ADB+∠BDC=∠ADB+2∠ADB=3∠ADB=150°,解得∠ADB=50°,故②正确
∵∠EAB=72°,∴∠DAN=180°-∠EAB=180°-72°=108°,
∴∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°,故③正确
∵AD∥BC,∴∠CBN=∠DAN=108°,故④正确
其中正确说法的个数是4个.
故选择D.
10、(2018·四川达州市·七年级期末)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 =___________.
【答案】
【解析】
∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=∠ABC,∠A1CA=∠ACD,
∵∠A1CD=∠A1+∠A1BC,
即∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD-∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=∠A,
以此类推∠A2=∠A1, ∠A3=∠A2,……∠An=∠An-1,
所以∠An=,所以=.
故答案是:.
二、填空题
11、(2021春 鹿城区校级月考)如图,平移图形M,使其与图形N可以拼成一个平行四边形,则图中α的度数是 .
【点拨】此题重点考查平行线的性质及三角形内角和定理,关键是正确地作出辅助线并找到两部分图形中相应的角的关系.利用三角形的外角等于与它不相邻的两个内角的和,可以求得α的度数.
【解析】解:如图,延长AB交CE于点D,
由平行线的性质,得∠BDC=180°﹣70°=110°,
又∵∠C=180°﹣150°=30°,
∴α=∠ABC=∠BDC+∠C=110°+30°=140°.
故答案为:140°.
12、(21-22黑龙江哈尔滨市第六十九中学校七上期末)如图所示,将三角形纸片沿DE折叠,使点C落在点C ′处,若EC′恰好与BC平行,且∠C=80°,则∠BDE=_____.
【答案】130°
【分析】本题主要考查了折叠的性质、平行线的性质等知识点,掌握折叠后完全重叠的三角形是全等形是解答本题的关键.
根据折叠的性质可得∠CED=∠C′ED.再根据平行的性质求得∠C=∠AEC′=80°,然后由平角为180°求得∠CED,最后根据∠BDE=∠C+∠CED求解即可.
【详解】解:∵△CED沿ED折叠后得到△C′ED,∠CED=∠C′ED.
∵EC′//BC,∴∠C=∠AEC ′=80°.
∵∠AEC ′+∠CED+∠C ′ED=180°,∴∠CED=50°.
∴∠BDE=∠C+∠CED=80°+50°=130°.
故答案是:130°.
13、(20-21黑龙江哈尔滨三十九中七上期中数)如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC= °.
【分析】根据矩形的性质得∠BAD=∠ABC=90°,再根据平行线的性质,由AE∥BD得到∠DAE=∠ADB=28°,接着根据折叠的性质得∠BAF=∠EAF=59°,然后根据三角形外角性质计算∠AFC的度数.
【解答】解:∵四边形ABCD为矩形,∴∠BAD=∠ABC=90°,
∵AE∥BD,∴∠DAE=∠ADB=28°,
∴∠BAE=∠BAD+∠DAE=90°+28°=118°,
∵矩形ABCD沿AF折叠,点B落在点E处,
∴∠BAF=∠EAF=∠BAE=×118°=59°,
∴∠AFC=∠BAF+∠ABF=59°+90°=149°.
故答案为149.
14、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
【答案】120
分析:此题考查了平行线的性质.注意掌握辅助线的作法,注意数形结合思想的应用.
先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
详解:如图,过点B作BF∥CD,
∵CD∥AE,∴CD∥BF∥AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=150°,∠BAE=90°,∴∠1=30°,∠2=90°,
∴∠ABC=∠1+∠2=120°.
故答案为120.
15、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,ab,∠1=30°,∠2=90°,则∠3的度数是 _______.
【答案】120°
【解析】
【分析】本题考查了平行线的性质以及三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题.
反向延长∠2的边与a交于一点,根据三角形外角的性质和平行线的性质即可得到结论.
【详解】解:如图,反向延长∠2的边与a交于一点,
∵∠2=90°,∠1=30°,
∴∠4=180°-∠2+∠1=120°,
∵ab,
∴∠3=∠4=120°,
故答案为:120°.
16、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,,,则____.
【答案】95°
【分析】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
过点E作EF∥AB,可得∠BEF+∠ABE=180°,从而得到∠BEF=60°,再由AB//CD,可得∠FEC=∠DCE,从而得到∠FEC=35°,即可求解.
【详解】解:如图,过点E作EF∥AB,
∵EF//AB,∴∠BEF+∠ABE=180°,
∵∠ABE=120°,∴∠BEF=180°-∠ABE=180°-120°=60°,
∵EF//AB,AB//CD,∴EF//CD,∴∠FEC=∠DCE,
∵∠DCE=35°,∴∠FEC=35°,∴∠BEC=∠BEF+∠FEC=60°+35°=95°.
故答案为:95°
17、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,和的平分线相交于,,求的度数_____.
【答案】110°##110度
【解析】
【分析】本题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.另外过点E作EH∥AB,也是解题的关键.
过点E作EH∥AB,然后由AB∥CD,可得AB∥EH∥CD,然后根据两直线平行内错角相等可得∠ABE=∠BEH,∠CDE=∠DEH,然后根据周角的定义可求∠ABE+∠CDE的度数;再根据角平分线的定义求出∠EBF+∠EDF的度数,然后根据四边形的内角和定理即可求∠BFD的度数.
【详解】解:过点E作EH∥AB,如图所示,
∵AB∥CD,∴AB∥EH∥CD,∴∠ABE=∠BEH,∠CDE=∠DEH,
∵∠BEH+∠DEH+∠BED=360°,∠BED=140°,
∴∠BEH+∠DEH=220°,∴∠ABE+∠CDE=220°,
∵∠ABE和∠CDE的平分线相交于F,∴∠EBF+∠EDF=(∠ABE+∠CDE)=110°,
∵∠BFD+∠BED+∠EBF+∠EDF=360°,∴∠BFD=110°.
故答案为:110°.
18、(20-21吉林长春德惠七上期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
【分析】根据平行线的性质得到∠2+∠PRQ=180°,∠3=∠SRQ=120°,求出∠PRQ的度数,根据∠1=∠SRQ﹣∠PRQ代入即可求出答案.
【解答】解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
三、解答题
19、(20-21黑龙江哈尔滨三十九中七上期中数)如图,方格纸中每个小正方形的边长均为1.在图中平移三角形ABC,使点A移到点D处,点B的对应点为点E,点C的对应点为点F.
(1)请在方格纸中画出平移后的三角形DEF;
(2)分别连接CD,CF,请直接写出三角形CDF的面积;
(3)过点D作CF的垂线,垂足为H,延长AB交直线DH于点G,请画出图形;直接写出四边形BGHC的面积.
【分析】(1)根据平移条件画出图形即可;
(2)根据面积公式解答即可;
(3)根据用分割法求四边形的面积解答即可.
【解答】解:(1)如图所示,△DEF即为所求:
(2)△CDF的面积=,
(3)四边形BGHC的面积==4.5.
20、(2021·江苏江宁·八年级开学考试)如图,,,点是边上一点,连接交 的延长线于点.点是边上一点.使得,作的角平分线交于点,若,求的度数.
【答案】40°
【分析】本题考查的是平行线的性质,涉及到角平分线、外角定理,本题关键是掌握有关定理、定义,题目难度较大.
由,,可得,从而由可得;由得,又有,故在中,,故,即可等量代换求解.
【详解】
解:,,,
的角平分线为,,
,,
而,,,
,,
,
∴在中,,
即,,
.
21、(21-22黑龙江大庆市肇源县七上期末)完成下面的证明
如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD(___________________)
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD(__________________)
∴________=∠BCF(等量代换)
∴BECF(______________________)
∴________=∠F(_________________)
∵BE⊥AF(已知)
∴________=90°(___________________)
∴∠F=90°.
【答案】两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,垂直的定义,熟练掌握相关知识是解题的关键.
根据平行线的性质得到∠ABC=∠BCD,再根据角平分线的定义进而得到∠EBC=∠BCF,即可判定BE∥CF,根据平行线的性质得出∠BEF=∠F,再根据垂直的定义即可得解.
【详解】证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
22、(21-22黑龙江哈尔滨南岗区萧红中学七上期中(人教五四))如图,在三角形ABC中,D,E,F分别是三边上点,且DE平分∠ADF,∠ADF=2∠DFB.
(1)判断DE与BC是否平行,并说明理由.
(2)若EF∥AB,∠DFE=3∠CFE,求∠ADE度数.
【答案】(1)DE与BC平行,证明见解析;(2)
【解析】
【分析】(1)本题主要考查了平行线的性质,即内错角相等,两直线平行,明确此知识即可作答;
(2)本题反复使用等量替换,借助两直线平行,内错角相等,找到角与角的等量关系进行替换,再根据平角为180°进行计算.
(1)根据DE平分,可以得到,又因为,从而可以得到,即可证明DE与BC是平行的位置关系;
(2)由(1)可知,,又根据,所以可以得到,再根据题目中,从而可以计算出的度数.
【详解】(1)DE与BC平行,证明如下:
∵DE平分,∴
∵,∴,∴
故DE与BC平行得证;
(2)由(1)可知,,
∵,∴,
∵,∴,∴
∵,∴
∴,∴
故最后答案为:.
23、(21-22黑龙江大庆市龙凤区上期中)已知:如图,EF∥CD,.
(1)判断与的位置关系,并说明理由.
(2)若平分,平分,且,求的度数.
【答案】(1)平行,理由见解析;(2)80°
【解析】
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,解题的关键在于能够熟练掌握平行线的性质与判定条件以及角平分线的定义.
(1)根据可得,再由可得由此即可证明;
(2)由平行线的性质可得,再由角平分线的定义可得,则,由此即可得到答案.
【详解】解:(1).
理由:,,
又,,;
(2),,
平分,,∴,
平分,.
24、(21-22黑龙江大庆市龙凤区上期中)已知一个角的两边与另一个角的两边分别平行,分别结合下图,试探索这两个角的关系,并证明你的结论.
(1)如图1,AB∥EF,BC∥DE,与的关系是_____.
(2)如图2,AB∥EF,BC∥DE,与的关系是________________.
(3)经过上述证明,我们可以得到一个结论:
(4)若两个角的两边分别平行,且一个角比另一个角的倍少,则这两个角分别是多少度?
【答案】(1);(2);(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;(4)这两个角分别是,或,.
【分析】此题考查了平行线的性质,涉及了一元一次方程的求解,解题的关键是掌握平行线的性质,得出结论,列方程求解即可.
(1)根据平行线的性质求解即可;
(2)根据平行线的性质以及对顶角的性质求解即可;
(3)结合已知条件以及(1)(2)的结论求解即可;
(4)设其中一个角为,根据(3)的结论,列方程求解即可.
【详解】解:(1)∵∴
又∵∴∴;
故答案为
(2)∵∴
又∵∴
又∵∴;
故答案为
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
(4)解:设其中一个角为,列方程得或,故或,
所以或,
答:这两个角分别是,或,.
25、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
【答案】(1)证明见解析;(2);(3).
【分析】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.
(1)过点作,先根据平行线的性质可得,再根据平行公理推论可得,然后根据平行线的性质可得,由此即可得证;
(2)过点作,同(1)的方法,先根据平行线的性质得出,,从而可得,再根据垂直的定义可得,由此即可得出结论;
(3)过点作,延长至点,先根据平行线的性质可得,,从而可得,再根据角平分线的定义、结合(2)的结论可得,然后根据角的和差、对顶角相等可得,由此即可得出答案.
【详解】证明:(1)如图,过点作,,
,,
,即,
,;
(2)如图,过点作,,
,,,即,
,,
,,;
(3)如图,过点作,延长至点,,
,,,平分,平分,
,
由(2)可知,,
,
又,
.
26、 (21-22黑龙江哈尔滨市香坊区七上期末)已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,
∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,
求∠GMH的度数.
【答案】(1)见详解;(2)∠MEB=40°,(3)∠GMH=80°
【解析】
【分析】本题考查平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组,掌握平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组是解题关键.
(1)根据等角的补角性质得出∠ABD=∠CDV,根据同位角相等两直线平行可得AB∥CD;
(2)根据AB∥CD;利用内错角相等得出∠ABD=∠RDB,根据BE∥DF,得出∠EBD=∠FDB,利用等量减等量差相等得出∠ABE=∠FDR,根据∠FDR=35°,可得∠ABE=∠FDR=35°即可;
(3)设ME交AB于S,根据MG∥EN,得出∠NES=∠GMS=∠GES,设∠NES=y°,可得∠NEG=∠NES+∠GES=2∠NES=2y°,根据∠EBD=2∠NEG,得出∠EBD =4∠NES=4y°,根据∠EDC=∠CDB,设∠EDC=x°,得出∠CDB=7x°,根据AB∥CD,得出∠GBE+∠EBD+∠CDB=180°,可得35+4y+7x=180根据三角形内角和∠BDE=∠BDC-∠EDC=7x-x=6x,∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,利用EB平分∠DEN,得出y°+40°=180°-4y°-6x°,解方程组,解得,可证ME∥UV,根据MH⊥UV,可求∠SMH=90°,∠SMG=∠NES=10°即可.
【详解】(1)证明:∵∠ABU+∠ABD=180°,∠ABU+∠CDV=180°.
∴∠ABU=180°-∠ABD,∠CDV=180°-∠ABU,∴∠ABD=∠CDV,∴AB∥CD;
(2)解:∵AB∥CD;∴∠ABD=∠RDB,∴∠ABE+∠EBD=∠FDB+∠FDR,
∵BE∥DF,∴∠EBD=∠FDB,∴∠ABE=∠FDR,
∵∠FDR=35°,∴∠ABE=∠FDR=35°,∴∠MEB=∠ABE+5°=35°+5°=40°,
(3)解:设ME交AB于S,
∵MG∥EN,∴∠NES=∠GMS=∠GES,
设∠NES=y°,
∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD =4∠NES=4y°,
∵∠EDC=∠CDB,设∠EDC=x°, ∴∠CDB=7x°,
∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,
∵∠BDE=∠BDC-∠EDC=7x-x=6x,
∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,
∵EB平分∠DEN,∴∠NEB=∠BED,
∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,
∴,解得,∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,
∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,
∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.
2021-2022学年苏科版七年级数学下册
一、选择题
1、(21-22黑龙江哈尔滨市香坊区七上期末) 在如图中,∠1和∠2不是同位角的是( )
A. B. C. D.
2、下列车标图案,可以看成由图形的平移得到的是( )
A.B. C.D.
3、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A. 第一次向左拐30°,第二次向右拐30° B. 第一次向左拐45°,第二次向左拐45°
C. 第一次向左拐60°,第二次向右拐120° D. 第一次向左拐53°,第二次向左拐127°
4、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,已知,, ,则 的度数为( )
A. 50° B. 55° C. 45° D. 60°
(4题) (5题) (6题)
5、(2019秋 奈曼旗期末)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,试着找一找这个规律,你发现的规律是( )
A.∠1+∠2=2∠A B.∠1+∠2=∠A C.∠A=2(∠1+∠2) D.∠1+∠2=∠A
6、(21-22黑龙江大庆市龙凤区上期中)如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( )
A. 85° B. 95° C. 90° D. 80°
7、(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
(7题) (8题) (9题)
8、(20-21黑龙江哈尔滨三十九中七上期中)如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个 B.6个 C.7个 D.8个
9、(21-22黑龙江哈尔滨市香坊区七上期末)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,∠EAB=72°,以下四个说法:①∠CDF=30°;②∠ADB=50°;③∠ABD=22°;④∠CBN=108°
其中正确说法的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
10、(2018·四川达州市·七年级期末)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 =___________.
(10题) (11题) (12题)
二、填空题
11、(2021春 鹿城区校级月考)如图,平移图形M,使其与图形N可以拼成一个平行四边形,则图中α的度数是 .
12、(21-22黑龙江哈尔滨市第六十九中学校七上期末)如图所示,将三角形纸片沿DE折叠,使点C落在点C ′处,若EC′恰好与BC平行,且∠C=80°,则∠BDE=_____.
13、(20-21黑龙江哈尔滨三十九中七上期中数)如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC= °.
(13题) (14题) (15题)
14、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
15、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,ab,∠1=30°,∠2=90°,则∠3的度数是 _______.
16、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,,,则____.
(16题) (17题) (18题)
17、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,和的平分线相交于,,求的度数_____.
18、(20-21吉林长春德惠七上期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
三、解答题
19、(20-21黑龙江哈尔滨三十九中七上期中数)如图,方格纸中每个小正方形的边长均为1.在图中平移三角形ABC,使点A移到点D处,点B的对应点为点E,点C的对应点为点F.
(1)请在方格纸中画出平移后的三角形DEF;
(2)分别连接CD,CF,请直接写出三角形CDF的面积;
(3)过点D作CF的垂线,垂足为H,延长AB交直线DH于点G,请画出图形;直接写出四边形BGHC的面积.
20、(2021·江苏江宁·八年级开学考试)如图,,,点是边上一点,连接交 的延长线于点.点是边上一点.使得,作的角平分线交于点,若,求的度数.
21、(21-22黑龙江大庆市肇源县七上期末)完成下面的证明
如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD(___________________)
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD(__________________)
∴________=∠BCF(等量代换)
∴BECF(______________________)
∴________=∠F(_________________)
∵BE⊥AF(已知)
∴________=90°(___________________)
∴∠F=90°.
22、(21-22黑龙江哈尔滨南岗区萧红中学七上期中(人教五四))如图,在三角形ABC中,D,E,F分别是三边上点,且DE平分∠ADF,∠ADF=2∠DFB.
(1)判断DE与BC是否平行,并说明理由.
(2)若EF∥AB,∠DFE=3∠CFE,求∠ADE度数.
23、(21-22黑龙江大庆市龙凤区上期中)已知:如图,EF∥CD,.
(1)判断与的位置关系,并说明理由.
(2)若平分,平分,且,求的度数.
24、(21-22黑龙江大庆市龙凤区上期中)已知一个角的两边与另一个角的两边分别平行,分别结合下图,试探索这两个角的关系,并证明你的结论.
(1)如图1,AB∥EF,BC∥DE,与的关系是_____.
(2)如图2,AB∥EF,BC∥DE,与的关系是________________.
(3)经过上述证明,我们可以得到一个结论:
(4)若两个角的两边分别平行,且一个角比另一个角的倍少,则这两个角分别是多少度?
25、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
26、 (21-22黑龙江哈尔滨市香坊区七上期末)已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,
∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,
求∠GMH的度数.
第7章 平面图形的认识(二) 单元整合练习题(培优)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、(21-22黑龙江哈尔滨市香坊区七上期末) 在如图中,∠1和∠2不是同位角的是( )
A. B. C. D.
【答案】D
【解析】
【分析】本题题考查三线八角中的同位角识别,解题关键在于掌握判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
同位角的定义:两条直线a,b被第三条直线c所截,在截线c的同侧,被截两直线a,b的同一方向的两个角,我们把这样的两个角称为同位角,依此即可求解.
【详解】解:A、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D、∠1与∠2的一边不在同一条直线上,不是同位角,符合题意.
故选:D.
2、下列车标图案,可以看成由图形的平移得到的是( )
A.B. C.D.
【分析】根据旋转变换,平移变换,轴对称变换对各选项分析判断后利用排除法求解.
【解答】解:A、可以由一个“基本图案”平移得到,故本选项符合题意;
B、不是由一个“基本图案”平移得到,故本选项不符合题意;
C、可以由一个“基本图案”旋转得到,故本选项不符合题意;
D、可以由一个“基本图案”旋转得到,故本选项不符合题意.
故选:A.
3、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A. 第一次向左拐30°,第二次向右拐30° B. 第一次向左拐45°,第二次向左拐45°
C. 第一次向左拐60°,第二次向右拐120° D. 第一次向左拐53°,第二次向左拐127°
【答案】D
【分析】本题考查了角的和差计算,正负数用表示生活中的角度的实际应用,理解角度和的意义,将所求问题转化为数学问题是解题关键.
根据规定向左拐的角度为正,向右拐的角度为负,两角之和为0°,与原方向相同,两角之和为90°,与原方向垂直,两角之和为180°,与原方向相反,找出两次拐弯的角度的和为即可得.
【详解】解:由题意,规定向左拐的角度为正,向右拐的角度为负,
A、第一次向左拐30°用+30°表示,第二次向右拐30°用-30°表示,∵,∴两次拐弯后的行驶方向与原来的方向相同,此项不符题意;
B、第一次向左拐45°用+45°表示,第二次向左拐45°用-45°表示,∵,∴两次拐弯后的行驶方向与原来的方向相同,此项不符题意;
C、第一次向左拐60°用+60°表示,第二次向右拐120°用-120°表示,∵,∴两次拐弯后的行驶方向与原来的方向成角,此项不符题意;
D、第一次向左拐53°用+53°表示,第二次向左拐127°用+127°表示,∵,∴两次拐弯后的行驶方向与原来的方向相反,此项符合题意;
故选:D.
4、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,已知,, ,则 的度数为( )
A. 50° B. 55° C. 45° D. 60°
【答案】B
【分析】本题考查了平行线的性质,三角形的内角和定理,外角的性质,熟悉相关性质是解题的关键.依据,得到,再根据,,即可得到,可得出.
详解】解:,
,
又,,
∴=,
故选:.
5、(2019秋 奈曼旗期末)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,试着找一找这个规律,你发现的规律是( )
A.∠1+∠2=2∠A B.∠1+∠2=∠A
C.∠A=2(∠1+∠2) D.∠1+∠2=∠A
【分析】本题考查了折叠的性质和三角形的内角和定理的应用,关键是得出等式∠ADE=90°-∠1,∠AED=90°-∠2,∠A=180°﹣(∠AED+∠ADE).
根据折叠得出∠ADE=∠A′DE,∠AED=∠A′ED,求出2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,推出∠ADE=90°-∠1,∠AED=90°-∠2,在△ADE中,∠A=180°﹣(∠AED+∠ADE),代入求出即可.
【解答】解:如图,延长BD和CE交于A′,
∵把△ABC沿DE折叠,当点A落在四边形BCDE内部,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,
∴∠ADE=90°-∠1,∠AED=90°-∠2,
∵在△ADE中,∠A=180°﹣(∠AED+∠ADE),
∴∠A=∠1+∠2,即2∠A=∠1+∠2.
故选:A.
6、(21-22黑龙江大庆市龙凤区上期中)如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( )
A. 85° B. 95° C. 90° D. 80°
【答案】B
【分析】本题主要考查翻折变换的知识,解答本题的关键是熟练掌握解题过程中应注意折叠前后的对应关系.
根据折叠前后图形全等和平行线,先求出∠CPR和∠CRP,再根据三角形内角和定理即可求出∠C.
【详解】因为折叠前后两个图形全等,C′P∥AB,C′R∥AD
∴∠CPR=∠C′PC =∠B=×120°=60°,
∠CRP=∠C′RC =∠D=×50°=25°;
∴∠C=180° 25° 60°=95°
故选:B.
7、(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
【答案】C
解:∵F是EC的中点,
∴,
∴,
∵ E是BD的中点 ,
∴,,
∵,
∴,
∴,
故选:C.
8、(20-21黑龙江哈尔滨三十九中七上期中)如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个 B.6个 C.7个 D.8个
【分析】依据平行线的性质,即可得到图中与∠B相等的角的个数.
【解答】解:∵AC∥DE,AB∥DF,
∴∠C=∠BDE,∠B=∠CDF,
又∵∠B=∠C,
∴∠C=∠BDE=∠B=∠CDF,
∵EF∥BC,
∴∠DEF=∠BDE,∠DFE=∠CDF,∠AEF=∠B,∠AFE=∠C,
∴与∠B相等的角为:∠BDE,∠CDF,∠C,∠DEF,∠DFE,∠AEF,∠AFE,
∴图中与∠B相等的角(∠B除外)有7个,
故选:C.
9、(21-22黑龙江哈尔滨市香坊区七上期末)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,∠EAB=72°,以下四个说法:①∠CDF=30°;②∠ADB=50°;③∠ABD=22°;④∠CBN=108°
其中正确说法的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【分析】本题考查平行线性质,角的倍分,邻补角性质,三角形内角和,一元一次方程,掌握平行线性质,邻补角性质,三角形内角和,一元一次方程地解题关键.
根据AD∥BC,∠C=30°,利用内错角相等得出∠FDC=∠C=30°,可判断①正确;根据邻补角性质可求∠ADC=180°-∠FDC=180°-30°=150°,根据∠ADB:∠BDC=1:2,得出方程3∠ADB=150°,解方程可判断②正确;根据∠EAB=72°,可求邻补角∠DAN=180°-∠EAB=180°-72°=108°,利用三角形内角和可求∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°可判断③正确,利用AD∥BC,同位角相等的∠CBN=∠DAN=108°可判断④正确即可.
【详解】解:∵AD∥BC,∠C=30°,∴∠FDC=∠C=30°,故①正确;
∴∠ADC=180°-∠FDC=180°-30°=150°,
∵∠ADB:∠BDC=1:2,∴∠BDC=2∠ADB,
∵∠ADC=∠ADB+∠BDC=∠ADB+2∠ADB=3∠ADB=150°,解得∠ADB=50°,故②正确
∵∠EAB=72°,∴∠DAN=180°-∠EAB=180°-72°=108°,
∴∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°,故③正确
∵AD∥BC,∴∠CBN=∠DAN=108°,故④正确
其中正确说法的个数是4个.
故选择D.
10、(2018·四川达州市·七年级期末)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 =___________.
【答案】
【解析】
∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=∠ABC,∠A1CA=∠ACD,
∵∠A1CD=∠A1+∠A1BC,
即∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD-∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=∠A,
以此类推∠A2=∠A1, ∠A3=∠A2,……∠An=∠An-1,
所以∠An=,所以=.
故答案是:.
二、填空题
11、(2021春 鹿城区校级月考)如图,平移图形M,使其与图形N可以拼成一个平行四边形,则图中α的度数是 .
【点拨】此题重点考查平行线的性质及三角形内角和定理,关键是正确地作出辅助线并找到两部分图形中相应的角的关系.利用三角形的外角等于与它不相邻的两个内角的和,可以求得α的度数.
【解析】解:如图,延长AB交CE于点D,
由平行线的性质,得∠BDC=180°﹣70°=110°,
又∵∠C=180°﹣150°=30°,
∴α=∠ABC=∠BDC+∠C=110°+30°=140°.
故答案为:140°.
12、(21-22黑龙江哈尔滨市第六十九中学校七上期末)如图所示,将三角形纸片沿DE折叠,使点C落在点C ′处,若EC′恰好与BC平行,且∠C=80°,则∠BDE=_____.
【答案】130°
【分析】本题主要考查了折叠的性质、平行线的性质等知识点,掌握折叠后完全重叠的三角形是全等形是解答本题的关键.
根据折叠的性质可得∠CED=∠C′ED.再根据平行的性质求得∠C=∠AEC′=80°,然后由平角为180°求得∠CED,最后根据∠BDE=∠C+∠CED求解即可.
【详解】解:∵△CED沿ED折叠后得到△C′ED,∠CED=∠C′ED.
∵EC′//BC,∴∠C=∠AEC ′=80°.
∵∠AEC ′+∠CED+∠C ′ED=180°,∴∠CED=50°.
∴∠BDE=∠C+∠CED=80°+50°=130°.
故答案是:130°.
13、(20-21黑龙江哈尔滨三十九中七上期中数)如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC= °.
【分析】根据矩形的性质得∠BAD=∠ABC=90°,再根据平行线的性质,由AE∥BD得到∠DAE=∠ADB=28°,接着根据折叠的性质得∠BAF=∠EAF=59°,然后根据三角形外角性质计算∠AFC的度数.
【解答】解:∵四边形ABCD为矩形,∴∠BAD=∠ABC=90°,
∵AE∥BD,∴∠DAE=∠ADB=28°,
∴∠BAE=∠BAD+∠DAE=90°+28°=118°,
∵矩形ABCD沿AF折叠,点B落在点E处,
∴∠BAF=∠EAF=∠BAE=×118°=59°,
∴∠AFC=∠BAF+∠ABF=59°+90°=149°.
故答案为149.
14、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
【答案】120
分析:此题考查了平行线的性质.注意掌握辅助线的作法,注意数形结合思想的应用.
先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
详解:如图,过点B作BF∥CD,
∵CD∥AE,∴CD∥BF∥AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=150°,∠BAE=90°,∴∠1=30°,∠2=90°,
∴∠ABC=∠1+∠2=120°.
故答案为120.
15、(21-22黑龙江大庆杜尔伯特蒙古族自治县七上期末)如图,ab,∠1=30°,∠2=90°,则∠3的度数是 _______.
【答案】120°
【解析】
【分析】本题考查了平行线的性质以及三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题.
反向延长∠2的边与a交于一点,根据三角形外角的性质和平行线的性质即可得到结论.
【详解】解:如图,反向延长∠2的边与a交于一点,
∵∠2=90°,∠1=30°,
∴∠4=180°-∠2+∠1=120°,
∵ab,
∴∠3=∠4=120°,
故答案为:120°.
16、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,,,则____.
【答案】95°
【分析】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
过点E作EF∥AB,可得∠BEF+∠ABE=180°,从而得到∠BEF=60°,再由AB//CD,可得∠FEC=∠DCE,从而得到∠FEC=35°,即可求解.
【详解】解:如图,过点E作EF∥AB,
∵EF//AB,∴∠BEF+∠ABE=180°,
∵∠ABE=120°,∴∠BEF=180°-∠ABE=180°-120°=60°,
∵EF//AB,AB//CD,∴EF//CD,∴∠FEC=∠DCE,
∵∠DCE=35°,∴∠FEC=35°,∴∠BEC=∠BEF+∠FEC=60°+35°=95°.
故答案为:95°
17、(21-22黑龙江大庆龙凤区七上期末)如图,已知ABCD,和的平分线相交于,,求的度数_____.
【答案】110°##110度
【解析】
【分析】本题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.另外过点E作EH∥AB,也是解题的关键.
过点E作EH∥AB,然后由AB∥CD,可得AB∥EH∥CD,然后根据两直线平行内错角相等可得∠ABE=∠BEH,∠CDE=∠DEH,然后根据周角的定义可求∠ABE+∠CDE的度数;再根据角平分线的定义求出∠EBF+∠EDF的度数,然后根据四边形的内角和定理即可求∠BFD的度数.
【详解】解:过点E作EH∥AB,如图所示,
∵AB∥CD,∴AB∥EH∥CD,∴∠ABE=∠BEH,∠CDE=∠DEH,
∵∠BEH+∠DEH+∠BED=360°,∠BED=140°,
∴∠BEH+∠DEH=220°,∴∠ABE+∠CDE=220°,
∵∠ABE和∠CDE的平分线相交于F,∴∠EBF+∠EDF=(∠ABE+∠CDE)=110°,
∵∠BFD+∠BED+∠EBF+∠EDF=360°,∴∠BFD=110°.
故答案为:110°.
18、(20-21吉林长春德惠七上期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
【分析】根据平行线的性质得到∠2+∠PRQ=180°,∠3=∠SRQ=120°,求出∠PRQ的度数,根据∠1=∠SRQ﹣∠PRQ代入即可求出答案.
【解答】解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
三、解答题
19、(20-21黑龙江哈尔滨三十九中七上期中数)如图,方格纸中每个小正方形的边长均为1.在图中平移三角形ABC,使点A移到点D处,点B的对应点为点E,点C的对应点为点F.
(1)请在方格纸中画出平移后的三角形DEF;
(2)分别连接CD,CF,请直接写出三角形CDF的面积;
(3)过点D作CF的垂线,垂足为H,延长AB交直线DH于点G,请画出图形;直接写出四边形BGHC的面积.
【分析】(1)根据平移条件画出图形即可;
(2)根据面积公式解答即可;
(3)根据用分割法求四边形的面积解答即可.
【解答】解:(1)如图所示,△DEF即为所求:
(2)△CDF的面积=,
(3)四边形BGHC的面积==4.5.
20、(2021·江苏江宁·八年级开学考试)如图,,,点是边上一点,连接交 的延长线于点.点是边上一点.使得,作的角平分线交于点,若,求的度数.
【答案】40°
【分析】本题考查的是平行线的性质,涉及到角平分线、外角定理,本题关键是掌握有关定理、定义,题目难度较大.
由,,可得,从而由可得;由得,又有,故在中,,故,即可等量代换求解.
【详解】
解:,,,
的角平分线为,,
,,
而,,,
,,
,
∴在中,,
即,,
.
21、(21-22黑龙江大庆市肇源县七上期末)完成下面的证明
如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD(___________________)
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD(__________________)
∴________=∠BCF(等量代换)
∴BECF(______________________)
∴________=∠F(_________________)
∵BE⊥AF(已知)
∴________=90°(___________________)
∴∠F=90°.
【答案】两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,垂直的定义,熟练掌握相关知识是解题的关键.
根据平行线的性质得到∠ABC=∠BCD,再根据角平分线的定义进而得到∠EBC=∠BCF,即可判定BE∥CF,根据平行线的性质得出∠BEF=∠F,再根据垂直的定义即可得解.
【详解】证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
22、(21-22黑龙江哈尔滨南岗区萧红中学七上期中(人教五四))如图,在三角形ABC中,D,E,F分别是三边上点,且DE平分∠ADF,∠ADF=2∠DFB.
(1)判断DE与BC是否平行,并说明理由.
(2)若EF∥AB,∠DFE=3∠CFE,求∠ADE度数.
【答案】(1)DE与BC平行,证明见解析;(2)
【解析】
【分析】(1)本题主要考查了平行线的性质,即内错角相等,两直线平行,明确此知识即可作答;
(2)本题反复使用等量替换,借助两直线平行,内错角相等,找到角与角的等量关系进行替换,再根据平角为180°进行计算.
(1)根据DE平分,可以得到,又因为,从而可以得到,即可证明DE与BC是平行的位置关系;
(2)由(1)可知,,又根据,所以可以得到,再根据题目中,从而可以计算出的度数.
【详解】(1)DE与BC平行,证明如下:
∵DE平分,∴
∵,∴,∴
故DE与BC平行得证;
(2)由(1)可知,,
∵,∴,
∵,∴,∴
∵,∴
∴,∴
故最后答案为:.
23、(21-22黑龙江大庆市龙凤区上期中)已知:如图,EF∥CD,.
(1)判断与的位置关系,并说明理由.
(2)若平分,平分,且,求的度数.
【答案】(1)平行,理由见解析;(2)80°
【解析】
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,解题的关键在于能够熟练掌握平行线的性质与判定条件以及角平分线的定义.
(1)根据可得,再由可得由此即可证明;
(2)由平行线的性质可得,再由角平分线的定义可得,则,由此即可得到答案.
【详解】解:(1).
理由:,,
又,,;
(2),,
平分,,∴,
平分,.
24、(21-22黑龙江大庆市龙凤区上期中)已知一个角的两边与另一个角的两边分别平行,分别结合下图,试探索这两个角的关系,并证明你的结论.
(1)如图1,AB∥EF,BC∥DE,与的关系是_____.
(2)如图2,AB∥EF,BC∥DE,与的关系是________________.
(3)经过上述证明,我们可以得到一个结论:
(4)若两个角的两边分别平行,且一个角比另一个角的倍少,则这两个角分别是多少度?
【答案】(1);(2);(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;(4)这两个角分别是,或,.
【分析】此题考查了平行线的性质,涉及了一元一次方程的求解,解题的关键是掌握平行线的性质,得出结论,列方程求解即可.
(1)根据平行线的性质求解即可;
(2)根据平行线的性质以及对顶角的性质求解即可;
(3)结合已知条件以及(1)(2)的结论求解即可;
(4)设其中一个角为,根据(3)的结论,列方程求解即可.
【详解】解:(1)∵∴
又∵∴∴;
故答案为
(2)∵∴
又∵∴
又∵∴;
故答案为
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
(4)解:设其中一个角为,列方程得或,故或,
所以或,
答:这两个角分别是,或,.
25、(21-22黑龙江哈尔滨南岗区萧红中学七上期中)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
【答案】(1)证明见解析;(2);(3).
【分析】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.
(1)过点作,先根据平行线的性质可得,再根据平行公理推论可得,然后根据平行线的性质可得,由此即可得证;
(2)过点作,同(1)的方法,先根据平行线的性质得出,,从而可得,再根据垂直的定义可得,由此即可得出结论;
(3)过点作,延长至点,先根据平行线的性质可得,,从而可得,再根据角平分线的定义、结合(2)的结论可得,然后根据角的和差、对顶角相等可得,由此即可得出答案.
【详解】证明:(1)如图,过点作,,
,,
,即,
,;
(2)如图,过点作,,
,,,即,
,,
,,;
(3)如图,过点作,延长至点,,
,,,平分,平分,
,
由(2)可知,,
,
又,
.
26、 (21-22黑龙江哈尔滨市香坊区七上期末)已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,
∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,
求∠GMH的度数.
【答案】(1)见详解;(2)∠MEB=40°,(3)∠GMH=80°
【解析】
【分析】本题考查平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组,掌握平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组是解题关键.
(1)根据等角的补角性质得出∠ABD=∠CDV,根据同位角相等两直线平行可得AB∥CD;
(2)根据AB∥CD;利用内错角相等得出∠ABD=∠RDB,根据BE∥DF,得出∠EBD=∠FDB,利用等量减等量差相等得出∠ABE=∠FDR,根据∠FDR=35°,可得∠ABE=∠FDR=35°即可;
(3)设ME交AB于S,根据MG∥EN,得出∠NES=∠GMS=∠GES,设∠NES=y°,可得∠NEG=∠NES+∠GES=2∠NES=2y°,根据∠EBD=2∠NEG,得出∠EBD =4∠NES=4y°,根据∠EDC=∠CDB,设∠EDC=x°,得出∠CDB=7x°,根据AB∥CD,得出∠GBE+∠EBD+∠CDB=180°,可得35+4y+7x=180根据三角形内角和∠BDE=∠BDC-∠EDC=7x-x=6x,∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,利用EB平分∠DEN,得出y°+40°=180°-4y°-6x°,解方程组,解得,可证ME∥UV,根据MH⊥UV,可求∠SMH=90°,∠SMG=∠NES=10°即可.
【详解】(1)证明:∵∠ABU+∠ABD=180°,∠ABU+∠CDV=180°.
∴∠ABU=180°-∠ABD,∠CDV=180°-∠ABU,∴∠ABD=∠CDV,∴AB∥CD;
(2)解:∵AB∥CD;∴∠ABD=∠RDB,∴∠ABE+∠EBD=∠FDB+∠FDR,
∵BE∥DF,∴∠EBD=∠FDB,∴∠ABE=∠FDR,
∵∠FDR=35°,∴∠ABE=∠FDR=35°,∴∠MEB=∠ABE+5°=35°+5°=40°,
(3)解:设ME交AB于S,
∵MG∥EN,∴∠NES=∠GMS=∠GES,
设∠NES=y°,
∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD =4∠NES=4y°,
∵∠EDC=∠CDB,设∠EDC=x°, ∴∠CDB=7x°,
∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,
∵∠BDE=∠BDC-∠EDC=7x-x=6x,
∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,
∵EB平分∠DEN,∴∠NEB=∠BED,
∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,
∴,解得,∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,
∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,
∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
