2021-2022学年北师大版八年级数学下册1.3.2线段的垂直平分线课件(第二课时 18张)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册1.3.2线段的垂直平分线课件(第二课时 18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 10:35:41 | ||
图片预览






文档简介
(共18张PPT)
北师大版八年级下册第一章
线段的垂直平分线第二课时
了解和掌握三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
经历“操作-发现-猜想-证明”的过程,发展学生的演绎推理能力
教学目标
情景引入
如图,地面上有三个洞口A、B、C,老鼠可以从任
意一个洞口跑出,猫为能同时最省力地顾及到三个
洞口(到A、B、C三个点的距离相等),尽快抓到老
鼠,应该蹲守在哪里?
回顾思考
问题一:上节课我们学习了垂直平分线的相关内容,垂直平分线有哪些性质呢?我们是怎样得到的呢?
问题二:三角形有三条边,那有几条垂直平分线呢?这些垂直平分线会不会交于一点?谈谈你的看法。
A
B
C
D
活动探究一
活动一:准备好一张裁剪好的三角形,通过折叠找出每条边的垂直平分线,并用彩色笔画出折痕,观察这三条垂直平分线,你发现了什么?和同伴交流谈论一下。
①三角形有三条垂直平分线,三条垂直平分线会交于一点
②这一交点到三个顶点的距离相等。
活动探究二
活动二:请利用尺规作图作三角形的三条边的垂直平分线,观察这三条垂直平分线,与你刚刚的活动探究发现一样吗?
①三角形有三条垂直平分线,三条垂直平分线会交于一点
②这一交点到三个顶点的距离相等。
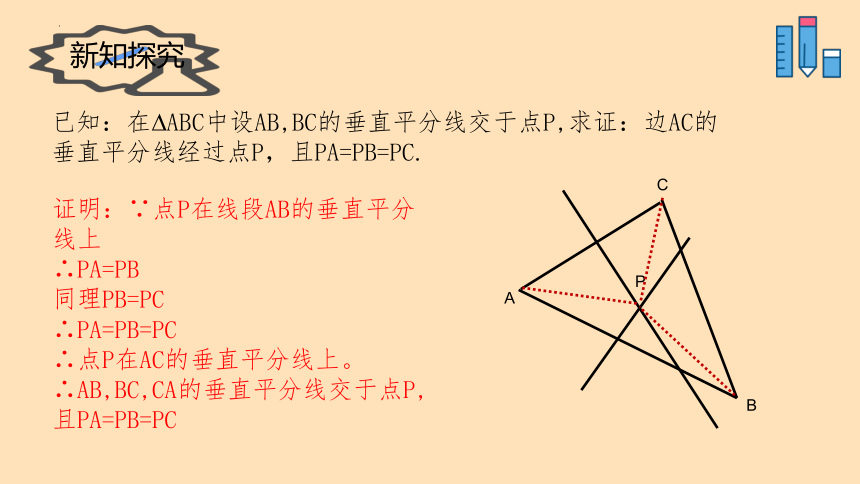
新知探究
已知:在 ABC中设AB,BC的垂直平分线交于点P,求证:边AC的垂直平分线经过点P,且PA=PB=PC.
证明:∵点P在线段AB的垂直平分线上
∴PA=PB
同理PB=PC
∴PA=PB=PC
∴点P在AC的垂直平分线上。
∴AB,BC,CA的垂直平分线交于点P,且PA=PB=PC
A
B
C
P
定理
三角形三条边的垂直平分线相交于一点,并且这个点到三个顶点的距离相等。
归纳总结
__________
例题1.如图,O是 ABC的两条垂直平分线的交点,
∠BAC=70°,则∠BOC=( )
A 120°
B 125°
C 130°
D 140
D
活学活用
例题2.某科技公司研制开发了一种监控违章车辆的电子仪器,如图,有三条两两相交的公路,你认为这个监控仪器安装在什么位置可离三个路口的交叉点的距离相等,以便及时进行监控
解:作法:如图所示,A,B,C代替三个路口,
①连接AB,BC
②分别作线段AB,BC的垂直平分线交于点P,则点P就是所求作的点
活学活用
活动探究三
活动3.已知三角形的一条边为5cm及这条边上的高3cm,你能作出三角形吗?如果能,是唯一的吗?
任务要求:
1.小组合作
2.自主完成
3.用时2分钟
不是唯一的,有无数条高。
活动4.已知等腰三角形的底边为5cm及底边上的高3cm,你能作出三角形吗 如果能,你作出的三角形还和同伴的不同吗?
任务要求:
1.小组合作
2.自主完成
3.用时2分钟
活动探究四
能,所作的等腰三角形是唯一确定的
如何通过尺规作图去作已知三角形一边的垂线呢?
活学活用
例题3.如图 ABC,要求尺规作图求作:
(1)AC边上的高
(2)BC边上的高
1.若点P是 ABC三边垂直平分线的交点,且PA=2cm,则PB= ______,PC=________
2cm
2cm
例题巩固
例题巩固
2.如果一个三角形两边的垂直平分线的交点在第三条边上,那么这个三角形是( )
A 锐角三角形
B 钝角三角形
C 直角三角形
D 不太确定
C
例题巩固
3.如图所示,∠A=52°,O是AB,AC的垂直平分线的交点,那么∠OCB=_____
解:如图,连接OA,OB,
∵O是AB,AC的垂直平分线的交点
∴OA=OB=OC,
∴∠1=∠2,∠5=∠6,∠3=∠4
∴2∠1+2∠3+2∠6=180
∴2∠6=180°-2∠BAC=180°-2×52°=76°
∴∠OCB=∠6=38°
38°
问题解决
如图,地面上有三个洞口A、B、C,老鼠可以从任
意一个洞口跑出,猫为能同时最省力地顾及到三个
洞口(到A、B、C三个点的距离相等),尽快抓到老
鼠,应该蹲守在哪里?
猫蹲守的位置为线段AB,线段AC,线段BC的垂直平分线的交点处。
课堂总结
三角形的三条垂直平分线有什么特点?
垂直平分线尺规作图有哪些应用?
北师大版八年级下册第一章
线段的垂直平分线第二课时
了解和掌握三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
经历“操作-发现-猜想-证明”的过程,发展学生的演绎推理能力
教学目标
情景引入
如图,地面上有三个洞口A、B、C,老鼠可以从任
意一个洞口跑出,猫为能同时最省力地顾及到三个
洞口(到A、B、C三个点的距离相等),尽快抓到老
鼠,应该蹲守在哪里?
回顾思考
问题一:上节课我们学习了垂直平分线的相关内容,垂直平分线有哪些性质呢?我们是怎样得到的呢?
问题二:三角形有三条边,那有几条垂直平分线呢?这些垂直平分线会不会交于一点?谈谈你的看法。
A
B
C
D
活动探究一
活动一:准备好一张裁剪好的三角形,通过折叠找出每条边的垂直平分线,并用彩色笔画出折痕,观察这三条垂直平分线,你发现了什么?和同伴交流谈论一下。
①三角形有三条垂直平分线,三条垂直平分线会交于一点
②这一交点到三个顶点的距离相等。
活动探究二
活动二:请利用尺规作图作三角形的三条边的垂直平分线,观察这三条垂直平分线,与你刚刚的活动探究发现一样吗?
①三角形有三条垂直平分线,三条垂直平分线会交于一点
②这一交点到三个顶点的距离相等。
新知探究
已知:在 ABC中设AB,BC的垂直平分线交于点P,求证:边AC的垂直平分线经过点P,且PA=PB=PC.
证明:∵点P在线段AB的垂直平分线上
∴PA=PB
同理PB=PC
∴PA=PB=PC
∴点P在AC的垂直平分线上。
∴AB,BC,CA的垂直平分线交于点P,且PA=PB=PC
A
B
C
P
定理
三角形三条边的垂直平分线相交于一点,并且这个点到三个顶点的距离相等。
归纳总结
__________
例题1.如图,O是 ABC的两条垂直平分线的交点,
∠BAC=70°,则∠BOC=( )
A 120°
B 125°
C 130°
D 140
D
活学活用
例题2.某科技公司研制开发了一种监控违章车辆的电子仪器,如图,有三条两两相交的公路,你认为这个监控仪器安装在什么位置可离三个路口的交叉点的距离相等,以便及时进行监控
解:作法:如图所示,A,B,C代替三个路口,
①连接AB,BC
②分别作线段AB,BC的垂直平分线交于点P,则点P就是所求作的点
活学活用
活动探究三
活动3.已知三角形的一条边为5cm及这条边上的高3cm,你能作出三角形吗?如果能,是唯一的吗?
任务要求:
1.小组合作
2.自主完成
3.用时2分钟
不是唯一的,有无数条高。
活动4.已知等腰三角形的底边为5cm及底边上的高3cm,你能作出三角形吗 如果能,你作出的三角形还和同伴的不同吗?
任务要求:
1.小组合作
2.自主完成
3.用时2分钟
活动探究四
能,所作的等腰三角形是唯一确定的
如何通过尺规作图去作已知三角形一边的垂线呢?
活学活用
例题3.如图 ABC,要求尺规作图求作:
(1)AC边上的高
(2)BC边上的高
1.若点P是 ABC三边垂直平分线的交点,且PA=2cm,则PB= ______,PC=________
2cm
2cm
例题巩固
例题巩固
2.如果一个三角形两边的垂直平分线的交点在第三条边上,那么这个三角形是( )
A 锐角三角形
B 钝角三角形
C 直角三角形
D 不太确定
C
例题巩固
3.如图所示,∠A=52°,O是AB,AC的垂直平分线的交点,那么∠OCB=_____
解:如图,连接OA,OB,
∵O是AB,AC的垂直平分线的交点
∴OA=OB=OC,
∴∠1=∠2,∠5=∠6,∠3=∠4
∴2∠1+2∠3+2∠6=180
∴2∠6=180°-2∠BAC=180°-2×52°=76°
∴∠OCB=∠6=38°
38°
问题解决
如图,地面上有三个洞口A、B、C,老鼠可以从任
意一个洞口跑出,猫为能同时最省力地顾及到三个
洞口(到A、B、C三个点的距离相等),尽快抓到老
鼠,应该蹲守在哪里?
猫蹲守的位置为线段AB,线段AC,线段BC的垂直平分线的交点处。
课堂总结
三角形的三条垂直平分线有什么特点?
垂直平分线尺规作图有哪些应用?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
