人教版九年级下册数学同步课时作业 27.2.1 第1课时 平行线分线段成比例(含答案)
文档属性
| 名称 | 人教版九年级下册数学同步课时作业 27.2.1 第1课时 平行线分线段成比例(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 13:48:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1. 如图,已知AB∥CD∥EF,BD∶DF=2∶5,那么下列结论正确的是( )
A.AC∶EC=2∶5 B.AB∶CD=2∶5
C.CD∶EF=2∶5 D.AC∶AE=2∶5
2. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
3. 如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,已知AB∥CD∥EF,AD∶AF=3∶5,BC=6,则CE的长为( )
A.5 B.4 C.3 D.2
5. 在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB.若BD=2AD,则的值为( )
A. B. C. D.
6. 如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( )
A.= B.= C.= D.=
7. 如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )
A.5 B.8.2 C.6.4 D.1.8
8. 如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF∶FC的值是( )
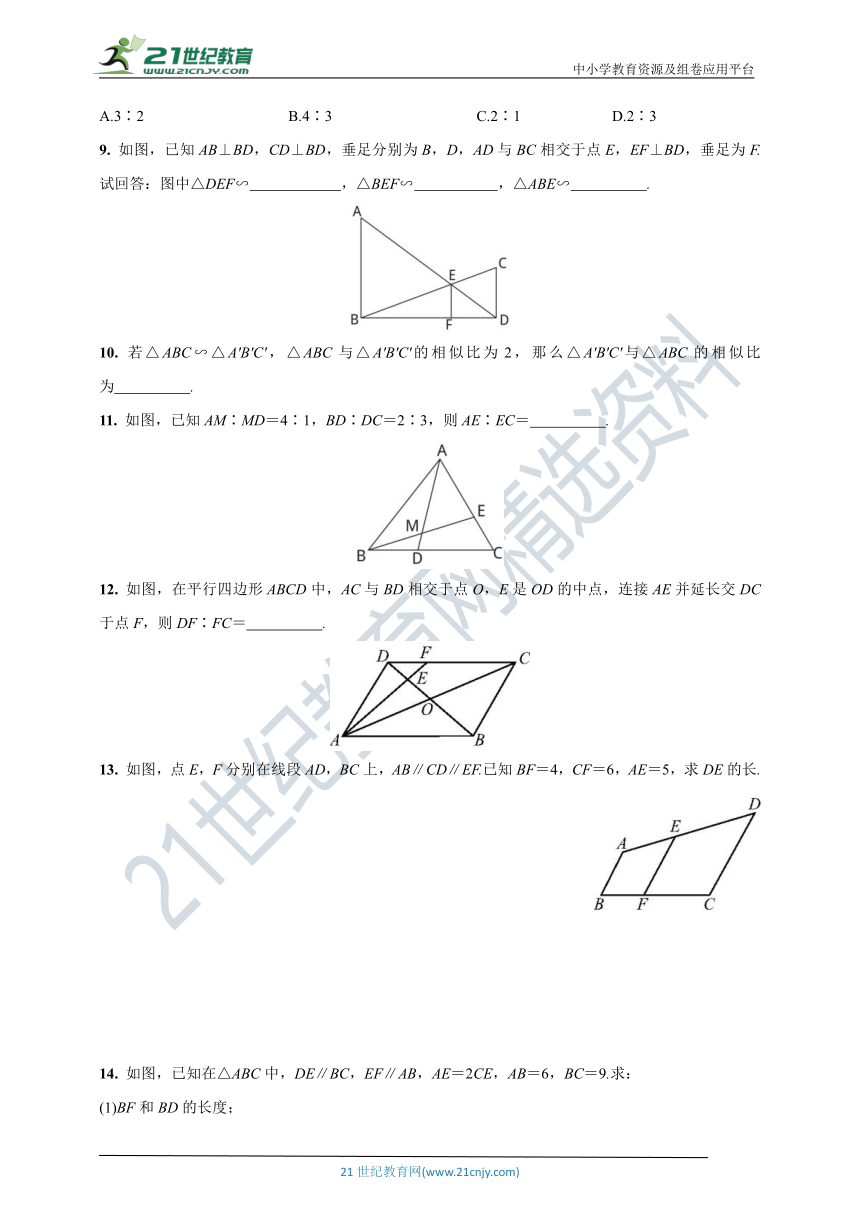
A.3∶2 B.4∶3 C.2∶1 D.2∶3
9. 如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ ,△BEF∽ ,△ABE∽ .
10. 若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 .
11. 如图,已知AM∶MD=4∶1,BD∶DC=2∶3,则AE∶EC= .
12. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC= .
13. 如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
14. 如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求:
(1)BF和BD的长度;
(2)四边形BDEF的周长.
15. 如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
16. 阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
参 考 答 案
1. A 2. C 3. D 4. B 5. A 6. C 7. D 8. A
9. △DAB △BCD △DCE
10. (或1∶2)
11. 8∶5
12. 1∶2
13. 解:∵AB∥CD∥EF,∴=,即=,解得DE=.
14. 解:(1)∵AE=2CE,∴=.∵EF∥AB,∴==.∵BC=9,∴BF=6.∵DE∥BC,∴==.∵AB=6,∴BD=2.
(2)∵EF∥AB,DE∥BC,∴四边形BDEF是平行四边形,∴BD=EF=2,DE=BF=6,∴四边形BDEF的周长为2×(2+6)=16.
15. 解:△ABC∽△DEF.理由:∵DE∥AB,∴△ODE∽△OAB,∴∠ODE=∠OAB,∠OED=∠OBA,==.同理可证∠ODF=∠OAC,∠OFD=∠OCA,∠OEF=∠OBC,∠OFE=∠OCB,==,==,∴∠EDF=∠BAC,∠DEF=∠ABC,∠DFE=∠ACB,==,∴△ABC∽△DEF.
16. 解:(1)∵CE∥AD,∴=,∠2=∠ACE,∠1=∠E.∵AD平分∠BAC,∴∠1=∠2,∴∠ACE=∠E,∴AE=AC,∴=.
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.∵AD平分∠BAC,∴=,即=,∴BD=,BC=,∴AD===,∴△ABD的周长为+3+=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1. 如图,已知AB∥CD∥EF,BD∶DF=2∶5,那么下列结论正确的是( )
A.AC∶EC=2∶5 B.AB∶CD=2∶5
C.CD∶EF=2∶5 D.AC∶AE=2∶5
2. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
3. 如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,已知AB∥CD∥EF,AD∶AF=3∶5,BC=6,则CE的长为( )
A.5 B.4 C.3 D.2
5. 在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB.若BD=2AD,则的值为( )
A. B. C. D.
6. 如图,AD∥BC,在△ABC中,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论错误的是( )
A.= B.= C.= D.=
7. 如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )
A.5 B.8.2 C.6.4 D.1.8
8. 如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF∶FC的值是( )
A.3∶2 B.4∶3 C.2∶1 D.2∶3
9. 如图,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AD与BC相交于点E,EF⊥BD,垂足为F.试回答:图中△DEF∽ ,△BEF∽ ,△ABE∽ .
10. 若△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为2,那么△A'B'C'与△ABC的相似比为 .
11. 如图,已知AM∶MD=4∶1,BD∶DC=2∶3,则AE∶EC= .
12. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF∶FC= .
13. 如图,点E,F分别在线段AD,BC上,AB∥CD∥EF.已知BF=4,CF=6,AE=5,求DE的长.
14. 如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求:
(1)BF和BD的长度;
(2)四边形BDEF的周长.
15. 如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗 说明理由.
16. 阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
参 考 答 案
1. A 2. C 3. D 4. B 5. A 6. C 7. D 8. A
9. △DAB △BCD △DCE
10. (或1∶2)
11. 8∶5
12. 1∶2
13. 解:∵AB∥CD∥EF,∴=,即=,解得DE=.
14. 解:(1)∵AE=2CE,∴=.∵EF∥AB,∴==.∵BC=9,∴BF=6.∵DE∥BC,∴==.∵AB=6,∴BD=2.
(2)∵EF∥AB,DE∥BC,∴四边形BDEF是平行四边形,∴BD=EF=2,DE=BF=6,∴四边形BDEF的周长为2×(2+6)=16.
15. 解:△ABC∽△DEF.理由:∵DE∥AB,∴△ODE∽△OAB,∴∠ODE=∠OAB,∠OED=∠OBA,==.同理可证∠ODF=∠OAC,∠OFD=∠OCA,∠OEF=∠OBC,∠OFE=∠OCB,==,==,∴∠EDF=∠BAC,∠DEF=∠ABC,∠DFE=∠ACB,==,∴△ABC∽△DEF.
16. 解:(1)∵CE∥AD,∴=,∠2=∠ACE,∠1=∠E.∵AD平分∠BAC,∴∠1=∠2,∴∠ACE=∠E,∴AE=AC,∴=.
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.∵AD平分∠BAC,∴=,即=,∴BD=,BC=,∴AD===,∴△ABD的周长为+3+=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
