2021-2022学年北师大版数学八年级下册1.1等腰三角形(第二课时)课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册1.1等腰三角形(第二课时)课时练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 703.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览




文档简介
等腰三角形(第二课时)
一、单选题
1.已知三角形三个内角的度数之比为3:3:4,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等边三角形
2.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
3.如图,在△ABC中,∠ABC=∠ACB,∠ABC与∠ACB的平分线相交于点O,过O作EFBC交AB于E,交AC于F,那么图中所有的等腰三角形个数是( )
A.4个 B.5个 C.6个 D.7个
4.如图,△ABC是等边三角形,点D在AC边上,∠DBC=40°,则∠ADB的度数为( )
A.25° B.60° C.90° D.100°
5.如图,在等腰直角三角形ABC中,∠BAC=90°,等边三角形ADE的顶点D在BC边上,连接CE,已知∠DCE=90°,CD=,则AB的长为( )
A. B. C. D.
6.如图,△ABC是等边三角形,点E是AC的中点,过点E作EF⊥AB于点F,延长BC交EF的反向延长线于点D,若EF=1,则DF的长为( )
A.2 B.2.5 C.3 D.3.5
7.点D、E分别是等边三角形的边、的中点,,F是AD上一动点,则的最小值是( )
A.6 B.7 C.8 D.9
8.如图,在中,,是高,是中线,是角平分线,交于G,交于H.下列结论:①;②;③;④.其中所有正确结论的序号是( )
A.①③ B.①②③ C.②③④ D.①②③④
9.如图,点E,F在线段BC上,△ABF与△DEC全等,点A和点D,点B和点C是对应点,AF和DE交于点M,则与EM相等的线段是( )
A.BE B.MF C.FC D.EF
10.如图所示,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.﹣ B. C.2+ D.2+
11.如图,上午8时,一艘船从处出发以15海里/小时的速度向正北航行,10时到达处,从两点望灯塔,测得,则处到灯塔的距离为( )
A.45海里 B.30海里 C.20海里 D.15海里
12.如图,已知∠AOB=60°,点P在边OA上,,点M,N在边OB上,,若MN=2,则OM=( ).
A.3 B.4 C.5 D.6
13.如图,△ABC中,∠C=90°,AB=8,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7.3
14.如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,则OP的长( )
A.15 B.14 C.11 D.12
二、填空题
15.如图,将宽为的纸条沿BC折叠,,则折叠后重叠部分的面积为____.(根号保留)
16.如图,在等边三角形ABC中,BD是AC边上的中线,过点D作于点E,若,则CE的长为______.
17.如图,在△ABC中.AB=AC,∠B=76°,以点C为圆心,CA长为半径作弧,交射线BC于点D,连接AD.则∠CAD的度数是_____°.
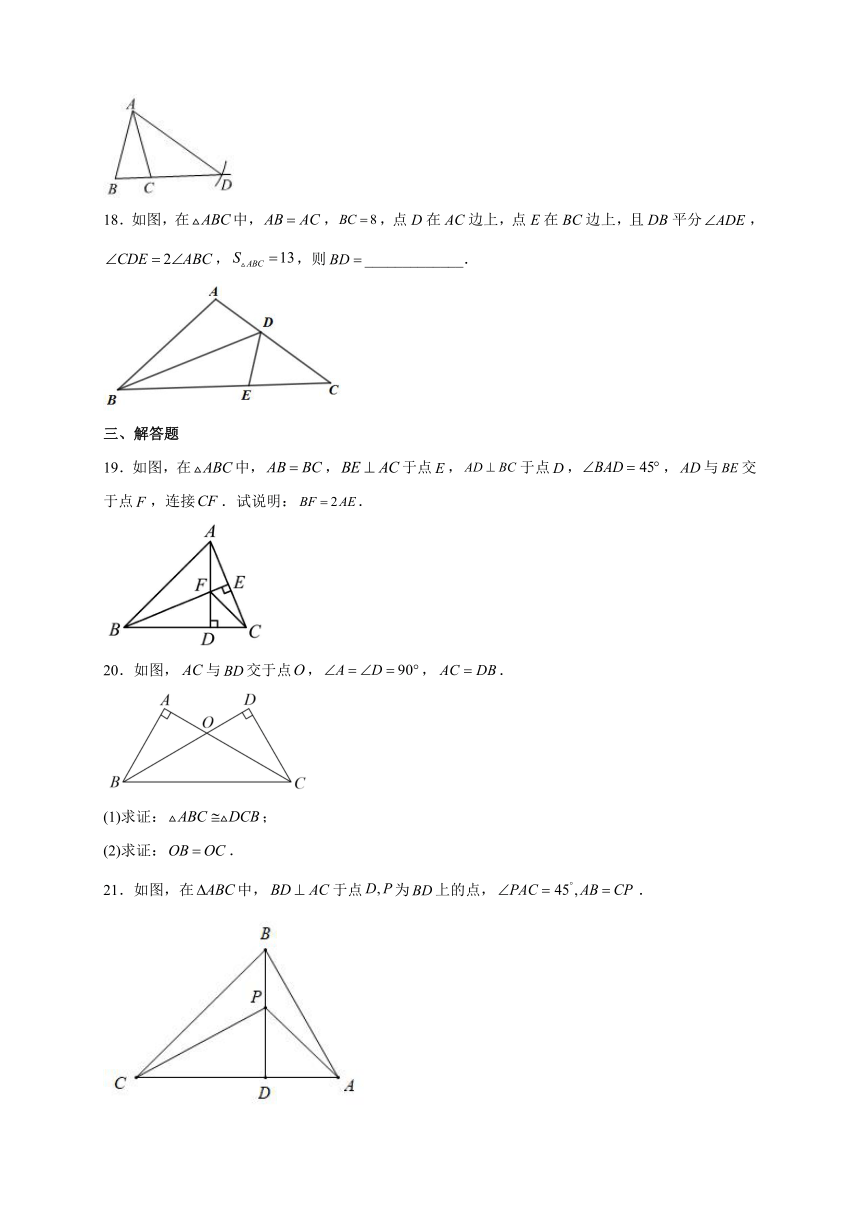
18.如图,在中,,,点D在AC边上,点E在BC边上,且DB平分,,,则_____________.
三、解答题
19.如图,在中,,于点,于点,,与交于点,连接.试说明:.
20.如图,与交于点,,.
(1)求证:;
(2)求证:.
21.如图,在中,于点为上的点,.
(1)求证:
(2)若求的长.
22.已知:如图,、都是等边三角形,、相交于点O,点M、N分别是线段、的中点.
(1)求证:;
(2)求的度数;
(3)求证:是等边三角形.
23.如图,△ABC中,AB=BC=CA=3,点D是边AB延长线上的一动点,分别以C,D为圆心,CD长为半径作弧,两弧在CD上方交于点E,连接EB并延长EB,交过点A且垂直于AD的直线于点F.
(1)求证:EB=DA;
(2)当时,求∠DEF的度数;
(3)在点D运动过程中,线段BF的长度是否会发生变化?若不会发生变化,则求出BF的长度;若会发生变化,请说明理由.
试卷第1页,共3页
参考答案:
1.A
解:(方法一)
设三角形最大的内角为4x°,则另外两个内角均为3x°,
依题意得:3x+3x+4x=180°,
解得:x=18,
∴3x°=3×18°=54°,4x°=4×18°=72°,
∴这个三角形是等腰三角形;
(方法二)
∵三角形三个内角的度数之比为3:3:4,
∴这个三角形为等腰三角形.
故选:A.
2.B
解:第一个图形中有两边相等,故第一个三角形是等腰三角形,
第二个图形中的三个角分别为50°,35°,95°,故第二个三角形不是等腰三角形;
第三个图形中的三个角分别为100°,40°,40°,故第三个三角形是等腰三角形;
第四个图形中的三个角分别为90°,45°,45°,故第四个三角形是等腰三角形;
故答案为:B.
3.B
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠OCB=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO,即△BEO,△CFO都为等腰三角形.
又∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形.
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE,
∴△AEF为等腰三角形.
∵∠ABC=∠ACB,∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠OCB,
∴OB=OC,即△BOC是等腰三角形.
故等腰三角形有:△ABC,△BEO,△CFO,△BOC,△AEF,
故选:B.
4.D
解:∵△ABC是等边三角形,
∴∠C=60°,
∵∠DBC=40°,
∴∠ADB=∠C+∠DBC=60°+40°=100°,
故选D.
5.B
解:∵△ABC为等腰直角三角形,△ADE为等边三角形,
∴∠BAC=90°,∠B=∠ACB=45°,AB=AC,∠DAE=∠ADE=∠AED=60°,AD=AE=DE,
又∵∠DCE=90°,
∴∠ACE=∠ACB=45°,即AC平分∠DCE,
又∵△ADE为等边三角形,AC平分∠DCE,
∴AC平分∠DAE,即∠DAC=∠EAC=30°,
在△ADC和△AEC中,,
∴△ADC≌△AEC,
∴DC=EC,
又∵AC平分∠DCE,
∴AC⊥DE,DF=FE,
∵CD=,
∴DC=EC=,
∴DE=2,则AD=AE=DE=2,
∴DF=FE=CF=1,
∴AF=,
∴AB=AC=,
故选:B.
.
6.C
解:连接BE,
∵△ABC是等边三角形,点E是AC的中点,
∴∠ABC=60°,∠ABE=∠CBE=30°,
∵EF⊥AB,
∴∠D=90°-∠ABC=30°,即∠D=∠CBE=30°,
∴BE=DE,
在Rt△BEF中,EF=1,
∴BE=2EF=2,
∴BE=DE=2,
∴DF=EF+DE=3,
故选:C.
7.A
解:连接,交AD于F,连接BF,则BF+EF最小(根据两点之间线段最短;点到直线垂直距离最短),
是的中点,是等边三角形,
由于C和B关于AD对称,则BF+EF=CF,
∵等边△ABC中,BD=CD,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CF=BF,
即BF+EF=CF+EF=CE,
∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CEB=90°,
在△ADB和△CEB中,
,
∴△ADB≌△CEB(AAS),
∴CE=AD=6,
即BF+EF=6.
故选A
8.B
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠BAG=2∠ACF,故②正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
9.B
解:∵△ABF与△DEC全等,点A与点D,点B与点C是对应顶点,
∴△ABF≌△DCE,
.
故选B
10.B
解:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
∴∠B=∠DAB,
∴BD=AD=,
在Rt△ADC中,∠C=90°,
∴DC===,
∴BC=BD+DC=
故选:B.
11.B
解:由题意得:(海里),
,
,
,
海里,
即处到灯塔的距离为30海里,
故选:B.
12.B
解:过P作,
∵,
∴为等腰三角形,
∵,
∴,
在中,,,
∴,
∴,
则.
故选:B.
13.A
解:∵∠C=90°,AB=8,∠B=30°,
∴AC=AB=×8=4,
∵点P是BC边上的动点,
∴4<AP<8,
∴AP的值不可能是3.5.
故选:A.
14.B
解:如图所示:延长NP交OM于点C,
∵,,
∴,
∵,,
∴,
在中,
∴,
∵,
∴,
∵,,
∴设,则,
∴在中,
即,
解得:或(舍去),
∴,
∴,
∴在中,
,
故选:B.
15.
解:如图,由折叠性质得:∠ECB=∠ACB
∵DE∥AB
∴∠DCA=∠CAB=45°
∵∠DCA+∠ACB+∠ECB=180°
∴
∵∠CAB+∠ACB+∠ABC=180°
∴∠ABC=∠ACB=67.5°
∴AB=AC
即△ABC是等腰三角形
过点C作CG⊥AB于点G,则CG=2,且∠ACG=∠CAB=45°
∴△CGA为等腰直角三角形
∴AG=CG=2
由勾股定理得:
∴
∴重叠部分△ABC的面积为
故答案为:
16.##0.5
解:在等边三角形ABC中,,
∵BD是AC边上的中线,∴,
∵,
∴,
在中,,,
∴,∴,
故答案为:
17.38
解:由题意可得,AC=CD,
∵AB=AC,∠B=76°,
∴∠ACB=∠B=76°,
∵AC=CD,
∴∠CAD=∠CDA=∠ACB=38°,
故答案为:38.
18.
解:如图,过点作,交的延长线于点,过点作交的延长线于点,
设
则
DB平分,
又
故答案为:.
19.见解析
解:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
20.(1)见解析
(2)见解析
解:(1)∵,
∴与都是直角三角形.
在与中,
∵,,
∴.
(2)解法一:∵,
∴,
∴.
解法二:∵,
∴,
∵,,
∴,
∴.
21.(1)见解析;(2).
解:(1)∵BD⊥AC,∠PAC=45°,
∴∠DPA=∠PAC =45°,
∴AD=DP,
且AB=CP,
∴Rt△ADB≌Rt△PDC(HL),
∴CD=BD;
(2)∵,∠DPA=45°,
∴∠CPD=60°,
又∵BD⊥AC,
∴∠PCD=30°,
∵AB=CP,
∴CP=2,
∴PD=1,
∴CD= .
∴BD=,
∴PB=.
22.(1)见解析
(2)
(3)见解析
(1)
解:∵、都是等边三角形,
∴,,,
∴,
∴,
在和中
,
∴,
∴.
(2)
解:∵,
∴,
∵等边三角形,
∴,
∴,
,
,
,
,
∴,
答:的度数是.
(3)
证明:∵,
∴,,
又∵点M、N分别是线段、的中点,
∴,,
∴,
在和中
,
∴,
∴,
,
又,
∴,
∴,
∴,
∴是等边三角形.
23.(1)见解析
(2)50°
(3)不会,6
解:
(1)
由题意可知:CD=DE=EC.
∴∠DCE=∠DEC=∠CDE=60°.
∵AB=BC=CA,
∴∠ABC=∠BCA=∠CAB=60°.
∴∠DCE=∠BCA.
∴∠DCE+∠DCB=∠BCA+∠DCB.
即:∠ECB=∠DCA.
在△EBC 和△DAC中
∴△EBC ≌△DAC(SAS).
∴EB=DA.
(2)
在△DAC中,
∠CDB=180°-∠DCA-∠CAB
=180°-110°-60°=10°.
∵△EBC ≌△DAC,
∴∠CEF=∠CDB=10°.
∴∠DEF=∠DEC-∠CEF=60°-10°=50°.
(3)
在点D运动过程中,线段BF的长度不会发生变化.
∵△EBC ≌△DAC,
∴∠EBC=∠CAB=60°.
∵∠DBC=180°-∠CBA=180°-60°=120°,
∴∠DBE=∠DBC-∠EBC=120°-60°=60°.
∴∠FBA=∠DBE=60°.
∵FA⊥DA,
∴∠FAB=90°.
∴∠F=90°-∠FBA=90°-60°=30°.
∴BF=2AB=2×3=6.
答案第1页,共2页
一、单选题
1.已知三角形三个内角的度数之比为3:3:4,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等边三角形
2.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
3.如图,在△ABC中,∠ABC=∠ACB,∠ABC与∠ACB的平分线相交于点O,过O作EFBC交AB于E,交AC于F,那么图中所有的等腰三角形个数是( )
A.4个 B.5个 C.6个 D.7个
4.如图,△ABC是等边三角形,点D在AC边上,∠DBC=40°,则∠ADB的度数为( )
A.25° B.60° C.90° D.100°
5.如图,在等腰直角三角形ABC中,∠BAC=90°,等边三角形ADE的顶点D在BC边上,连接CE,已知∠DCE=90°,CD=,则AB的长为( )
A. B. C. D.
6.如图,△ABC是等边三角形,点E是AC的中点,过点E作EF⊥AB于点F,延长BC交EF的反向延长线于点D,若EF=1,则DF的长为( )
A.2 B.2.5 C.3 D.3.5
7.点D、E分别是等边三角形的边、的中点,,F是AD上一动点,则的最小值是( )
A.6 B.7 C.8 D.9
8.如图,在中,,是高,是中线,是角平分线,交于G,交于H.下列结论:①;②;③;④.其中所有正确结论的序号是( )
A.①③ B.①②③ C.②③④ D.①②③④
9.如图,点E,F在线段BC上,△ABF与△DEC全等,点A和点D,点B和点C是对应点,AF和DE交于点M,则与EM相等的线段是( )
A.BE B.MF C.FC D.EF
10.如图所示,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.﹣ B. C.2+ D.2+
11.如图,上午8时,一艘船从处出发以15海里/小时的速度向正北航行,10时到达处,从两点望灯塔,测得,则处到灯塔的距离为( )
A.45海里 B.30海里 C.20海里 D.15海里
12.如图,已知∠AOB=60°,点P在边OA上,,点M,N在边OB上,,若MN=2,则OM=( ).
A.3 B.4 C.5 D.6
13.如图,△ABC中,∠C=90°,AB=8,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7.3
14.如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,则OP的长( )
A.15 B.14 C.11 D.12
二、填空题
15.如图,将宽为的纸条沿BC折叠,,则折叠后重叠部分的面积为____.(根号保留)
16.如图,在等边三角形ABC中,BD是AC边上的中线,过点D作于点E,若,则CE的长为______.
17.如图,在△ABC中.AB=AC,∠B=76°,以点C为圆心,CA长为半径作弧,交射线BC于点D,连接AD.则∠CAD的度数是_____°.
18.如图,在中,,,点D在AC边上,点E在BC边上,且DB平分,,,则_____________.
三、解答题
19.如图,在中,,于点,于点,,与交于点,连接.试说明:.
20.如图,与交于点,,.
(1)求证:;
(2)求证:.
21.如图,在中,于点为上的点,.
(1)求证:
(2)若求的长.
22.已知:如图,、都是等边三角形,、相交于点O,点M、N分别是线段、的中点.
(1)求证:;
(2)求的度数;
(3)求证:是等边三角形.
23.如图,△ABC中,AB=BC=CA=3,点D是边AB延长线上的一动点,分别以C,D为圆心,CD长为半径作弧,两弧在CD上方交于点E,连接EB并延长EB,交过点A且垂直于AD的直线于点F.
(1)求证:EB=DA;
(2)当时,求∠DEF的度数;
(3)在点D运动过程中,线段BF的长度是否会发生变化?若不会发生变化,则求出BF的长度;若会发生变化,请说明理由.
试卷第1页,共3页
参考答案:
1.A
解:(方法一)
设三角形最大的内角为4x°,则另外两个内角均为3x°,
依题意得:3x+3x+4x=180°,
解得:x=18,
∴3x°=3×18°=54°,4x°=4×18°=72°,
∴这个三角形是等腰三角形;
(方法二)
∵三角形三个内角的度数之比为3:3:4,
∴这个三角形为等腰三角形.
故选:A.
2.B
解:第一个图形中有两边相等,故第一个三角形是等腰三角形,
第二个图形中的三个角分别为50°,35°,95°,故第二个三角形不是等腰三角形;
第三个图形中的三个角分别为100°,40°,40°,故第三个三角形是等腰三角形;
第四个图形中的三个角分别为90°,45°,45°,故第四个三角形是等腰三角形;
故答案为:B.
3.B
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠OCB=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO,即△BEO,△CFO都为等腰三角形.
又∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形.
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE,
∴△AEF为等腰三角形.
∵∠ABC=∠ACB,∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠OCB,
∴OB=OC,即△BOC是等腰三角形.
故等腰三角形有:△ABC,△BEO,△CFO,△BOC,△AEF,
故选:B.
4.D
解:∵△ABC是等边三角形,
∴∠C=60°,
∵∠DBC=40°,
∴∠ADB=∠C+∠DBC=60°+40°=100°,
故选D.
5.B
解:∵△ABC为等腰直角三角形,△ADE为等边三角形,
∴∠BAC=90°,∠B=∠ACB=45°,AB=AC,∠DAE=∠ADE=∠AED=60°,AD=AE=DE,
又∵∠DCE=90°,
∴∠ACE=∠ACB=45°,即AC平分∠DCE,
又∵△ADE为等边三角形,AC平分∠DCE,
∴AC平分∠DAE,即∠DAC=∠EAC=30°,
在△ADC和△AEC中,,
∴△ADC≌△AEC,
∴DC=EC,
又∵AC平分∠DCE,
∴AC⊥DE,DF=FE,
∵CD=,
∴DC=EC=,
∴DE=2,则AD=AE=DE=2,
∴DF=FE=CF=1,
∴AF=,
∴AB=AC=,
故选:B.
.
6.C
解:连接BE,
∵△ABC是等边三角形,点E是AC的中点,
∴∠ABC=60°,∠ABE=∠CBE=30°,
∵EF⊥AB,
∴∠D=90°-∠ABC=30°,即∠D=∠CBE=30°,
∴BE=DE,
在Rt△BEF中,EF=1,
∴BE=2EF=2,
∴BE=DE=2,
∴DF=EF+DE=3,
故选:C.
7.A
解:连接,交AD于F,连接BF,则BF+EF最小(根据两点之间线段最短;点到直线垂直距离最短),
是的中点,是等边三角形,
由于C和B关于AD对称,则BF+EF=CF,
∵等边△ABC中,BD=CD,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CF=BF,
即BF+EF=CF+EF=CE,
∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CEB=90°,
在△ADB和△CEB中,
,
∴△ADB≌△CEB(AAS),
∴CE=AD=6,
即BF+EF=6.
故选A
8.B
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠BAG=2∠ACF,故②正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
9.B
解:∵△ABF与△DEC全等,点A与点D,点B与点C是对应顶点,
∴△ABF≌△DCE,
.
故选B
10.B
解:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
∴∠B=∠DAB,
∴BD=AD=,
在Rt△ADC中,∠C=90°,
∴DC===,
∴BC=BD+DC=
故选:B.
11.B
解:由题意得:(海里),
,
,
,
海里,
即处到灯塔的距离为30海里,
故选:B.
12.B
解:过P作,
∵,
∴为等腰三角形,
∵,
∴,
在中,,,
∴,
∴,
则.
故选:B.
13.A
解:∵∠C=90°,AB=8,∠B=30°,
∴AC=AB=×8=4,
∵点P是BC边上的动点,
∴4<AP<8,
∴AP的值不可能是3.5.
故选:A.
14.B
解:如图所示:延长NP交OM于点C,
∵,,
∴,
∵,,
∴,
在中,
∴,
∵,
∴,
∵,,
∴设,则,
∴在中,
即,
解得:或(舍去),
∴,
∴,
∴在中,
,
故选:B.
15.
解:如图,由折叠性质得:∠ECB=∠ACB
∵DE∥AB
∴∠DCA=∠CAB=45°
∵∠DCA+∠ACB+∠ECB=180°
∴
∵∠CAB+∠ACB+∠ABC=180°
∴∠ABC=∠ACB=67.5°
∴AB=AC
即△ABC是等腰三角形
过点C作CG⊥AB于点G,则CG=2,且∠ACG=∠CAB=45°
∴△CGA为等腰直角三角形
∴AG=CG=2
由勾股定理得:
∴
∴重叠部分△ABC的面积为
故答案为:
16.##0.5
解:在等边三角形ABC中,,
∵BD是AC边上的中线,∴,
∵,
∴,
在中,,,
∴,∴,
故答案为:
17.38
解:由题意可得,AC=CD,
∵AB=AC,∠B=76°,
∴∠ACB=∠B=76°,
∵AC=CD,
∴∠CAD=∠CDA=∠ACB=38°,
故答案为:38.
18.
解:如图,过点作,交的延长线于点,过点作交的延长线于点,
设
则
DB平分,
又
故答案为:.
19.见解析
解:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
20.(1)见解析
(2)见解析
解:(1)∵,
∴与都是直角三角形.
在与中,
∵,,
∴.
(2)解法一:∵,
∴,
∴.
解法二:∵,
∴,
∵,,
∴,
∴.
21.(1)见解析;(2).
解:(1)∵BD⊥AC,∠PAC=45°,
∴∠DPA=∠PAC =45°,
∴AD=DP,
且AB=CP,
∴Rt△ADB≌Rt△PDC(HL),
∴CD=BD;
(2)∵,∠DPA=45°,
∴∠CPD=60°,
又∵BD⊥AC,
∴∠PCD=30°,
∵AB=CP,
∴CP=2,
∴PD=1,
∴CD= .
∴BD=,
∴PB=.
22.(1)见解析
(2)
(3)见解析
(1)
解:∵、都是等边三角形,
∴,,,
∴,
∴,
在和中
,
∴,
∴.
(2)
解:∵,
∴,
∵等边三角形,
∴,
∴,
,
,
,
,
∴,
答:的度数是.
(3)
证明:∵,
∴,,
又∵点M、N分别是线段、的中点,
∴,,
∴,
在和中
,
∴,
∴,
,
又,
∴,
∴,
∴,
∴是等边三角形.
23.(1)见解析
(2)50°
(3)不会,6
解:
(1)
由题意可知:CD=DE=EC.
∴∠DCE=∠DEC=∠CDE=60°.
∵AB=BC=CA,
∴∠ABC=∠BCA=∠CAB=60°.
∴∠DCE=∠BCA.
∴∠DCE+∠DCB=∠BCA+∠DCB.
即:∠ECB=∠DCA.
在△EBC 和△DAC中
∴△EBC ≌△DAC(SAS).
∴EB=DA.
(2)
在△DAC中,
∠CDB=180°-∠DCA-∠CAB
=180°-110°-60°=10°.
∵△EBC ≌△DAC,
∴∠CEF=∠CDB=10°.
∴∠DEF=∠DEC-∠CEF=60°-10°=50°.
(3)
在点D运动过程中,线段BF的长度不会发生变化.
∵△EBC ≌△DAC,
∴∠EBC=∠CAB=60°.
∵∠DBC=180°-∠CBA=180°-60°=120°,
∴∠DBE=∠DBC-∠EBC=120°-60°=60°.
∴∠FBA=∠DBE=60°.
∵FA⊥DA,
∴∠FAB=90°.
∴∠F=90°-∠FBA=90°-60°=30°.
∴BF=2AB=2×3=6.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
